«Електромеханічне обладнання механізму повороту платформи ЕКГ-8І в умовах ПрАТ «ІнГЗК». дп. Реферат 6 Вступ Розділ Характеристики електромеханічного обладнання екскаватору екг8І 7

• Название: Реферат 6 Вступ Розділ Характеристики електромеханічного обладнання екскаватору екг8І 7
• Анкор: «Електромеханічне обладнання механізму повороту платформи ЕКГ-8І в умовах ПрАТ «ІнГЗК
• Дата: 12.05.2022
• Размер: 2.2 Mb.
• Имя файла: дп .docx
• Тип: Реферат; #525162
• страница: 8 из 14

2.3 Розрахунок енергетичних характеристик електропривода повороту

Залежність КПД електроприводу постійного струму від навантаження обчислюється за наступною формулою: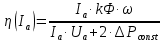



де ΔP_const – умовно постійні втрати електроенергії одного двигуна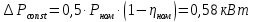



Залежність КПД електроприводу повороту від струму якірного кола зображено на рис.2.3.1.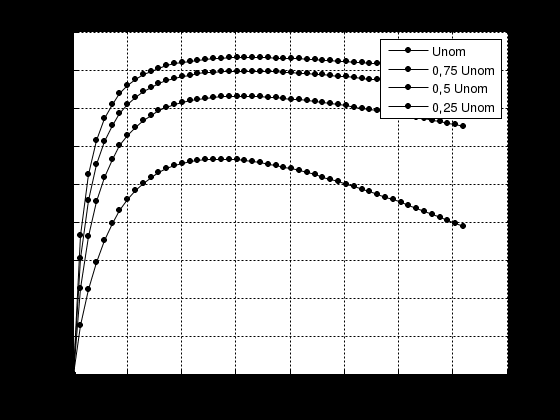


Рисунок 2.3.1 – Енергетичні характеристики приводу повороту екскаватора ЕКГ-8І по системі Г-Д
Значення коефіцієнту корисної дії електроприводу при ном. навантаженні складає 83%.

2.4 Розрахунок електромеханічних характеристик
електроприводу повороту по системі ТП-Д

Використавши формули, показані у розд.2.2, виконую розрахунок електромеханічних характеристик приводу повороту при живленні якірних кіл приводних двигунів від особистих тиристорних перетворювачів.

Результати цих розрахунків характеристик електропривода ТП-Д приведені нижче на рис.2.4.1, 2.4.2.

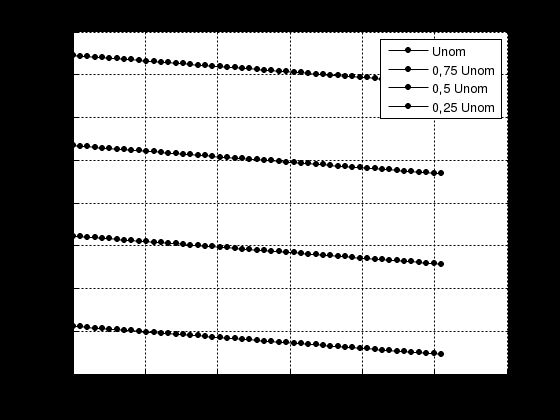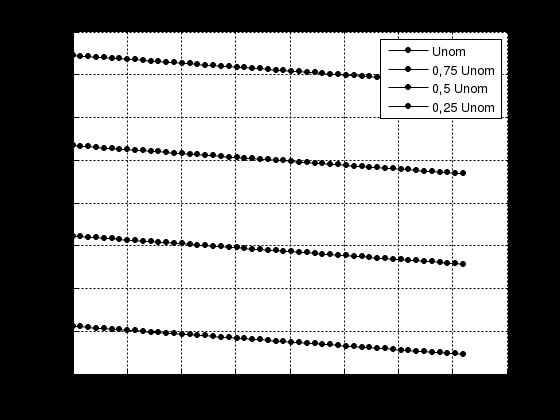
Рисунок 2.4.1 – Електромеханічні характеристики електроприводу повороту екскаватора ЕКГ-8И по системі ТП-Д

Статизм механічної характеристики приводу повороту



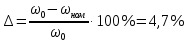
Статизм механічної характеристики приводу повороту при мінімальній напрузі на затискачах якоря



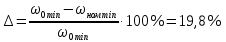
Залежність КПД приводу повороту від струму якірного кола зображена на рис.2.4.2.



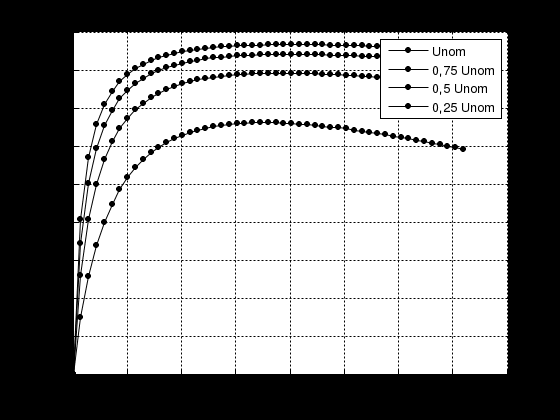
Рисунок 2.4.2 – Енергетичні характеристики приводу повороту екскаватора ЕКГ-8І по системі ТП-Д
Значення коефіцієнту корисної дії електроприводу при номінальному навантаженні складає 87%.

Висновки до другого розділу

У другому розділі виконано порівняльні розрахунки характеристик електроприводу повороту екскаватора ЕКГ-8И при роботі по системі «генератор-двигун» та при роботі по системі «тиристорний перетворювач - двигун». Характеристики електроприводу по системі Г-Д у необхідному діапазоні регулювання швидкості мають статизм від 8,2% до 33,5%. Характеристики електроприводу по системі ТП-Д у необхідному діапазоні регулювання швидкості мають статизм від 4,7% до 19,8%.Розраховано залежність коефіцієнту корисної дії електроприводу повороту екскаватора ЕКГ-8И. Значення коефіцієнту корисної дії електроприводу по системі Г-Д при номінальному навантаженні складає 83%. Значення коефіцієнту корисної дії електроприводу по системі ТП-Д при номінальному навантаженні складає 87%. При впровадженні системи ТП-Д взамін Г-Д коефіцієнт корисної дії електроприводу збільшується на 4%.

Розділ 3
МАТЕМАТИЧНЕ МОДЕЛЮВАННЯ ЕЛЕКТРОПРИВОДА ПОВОРОТУ ЕКСКАВАТОРА ЕКГ-8І

3.1 Математичне моделювання двигуна постійного струму

Відомо, що з рівнянь руху ротора та електричної рівноваги усіх контурів будь-якої електричної машини можна побудувати математичну модель цієї машини. У цьому випадку – це двигун постійного струму. На рисунках 3.1.1 а) та 3.1.1 б) позначені його принципова схема та схема заміщення відповідно.


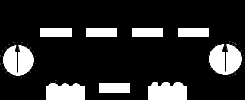
а) б)

Рис. 3.1.1. - Схеми двигуна постійного струму:

а) принципова; б) заміщення
Перед початком моделювання даного типу електричної машини, приймемо наступні припущення:

1. 
   Насиченням контуру основного магнітного потоку, контуру розсіювання, а також контуром вихрових струмів, нехтуємо;
   
2. 
   Струм збудження = const;
   
3. 
   Вплив реакції якоря відсутній (машина скомпенсована).
   

Виходячи з переліченого, параметри схеми заміщення, як і kφ=const. Тоді, за 2-м законом Кірхгофа рівняння електричної рівноваги:
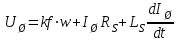, (3.1)

Рівняння руху електричного привода:

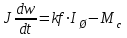(3.2)

Або у звичній формі:

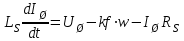(3.3)

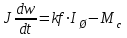(3.4)

Аналізуючи всі припущення та отримані рівняння, можна зробити висновок, що ця система рівнянь є лінійною, а значить її можна вирішити аналітичним шляхом.

Проте, параметри МПС змінні, тому і система стає нелінійною. Отож, розберемо випадок, коли зміна швидкості залежить від зміни величини магнітного потоку, враховуючи криву намагнічування. Тоді, зміна параметрів такої моделі при чисельному розв’язанні, враховується додаванням або алгебраїчних, або диференційних рівнянь. Також, для врахування особливостей роботи необхідно побудувати структурну схему машини постійного струму, для використання або математичних програм структурного моделювання, або самого моделювання на АОМ.

Таким чином, введемо електромагнітну сталу часу, а рівняння електричної рівноваги розділимо на _.

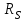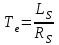(3.5)

В такому разі

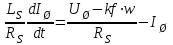(3.6)

або в операторній формі:

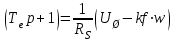(3.7)

Аперіодична ланка, вона ж передаточна функція за струмом, одержую, підставивши коефіцієнт передачі - :

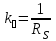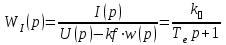(3.8)

Передаточну функцію інтегруючої ланки (вона ж передаточна функція за швидкістю) отримую з базового рівняння динаміки у операторній формі:

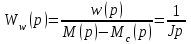(3.9)

З урахуванням виразів 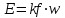та 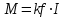складемо структурну схему у такому вигляді, котрий наведено на рис.3.1.2.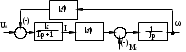




Рис. 3.1.2. - Структурна схема двигуна постійного струму незалежного збудження
Доповнення структурної схеми регуляторами й іншими елементами дозволяє досліджувати стійкість ЕМС та ін.