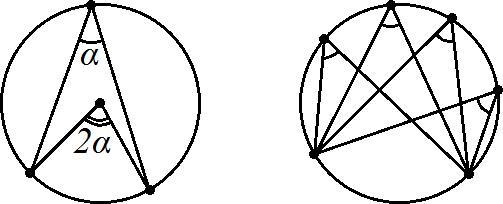Площадь произвольного выпуклого четырехугольника через диагонали и угол между ними:
S 1 d d
sin
2 1 2 Площадь произвольной фигуры в которую можно вписать окружность (в т.ч. площадь любого треугольника) может быть рассчитана через радиус вписанной окружности и полупериметр по очень важной формуле:
S = p∙r
По этой же формуле часто удобно находить и радиус вписанной окружности в некоторый многоугольник, в который её удалось вписать (в т.ч. любой треугольник): r Sp Свойства хорд и касательных: 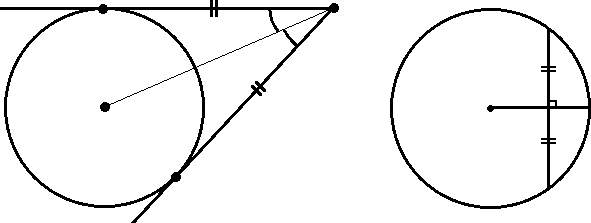 Теорема о пропорциональных отрезках хорд: 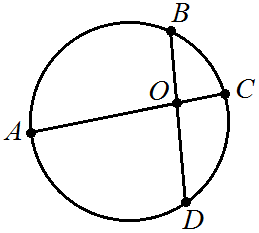 BO∙OD = AO∙OC Теорема о касательной и секущей и о двух секущих: 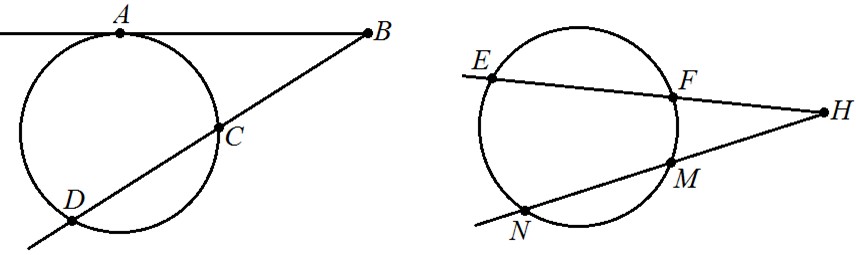 BA2 = BC∙ BD HF∙HE =HM∙HN Свойства центральных и вписанных углов: 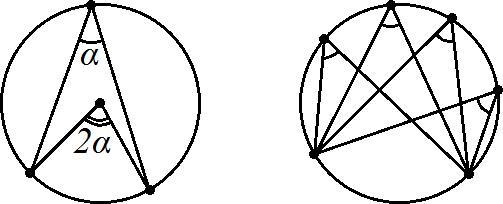 Свойство центральных углов и хорд: 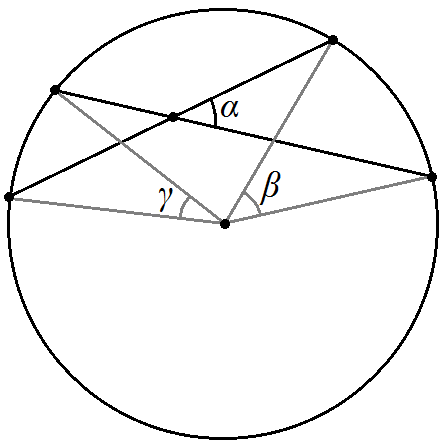 2
Свойство центральных углов и секущих:
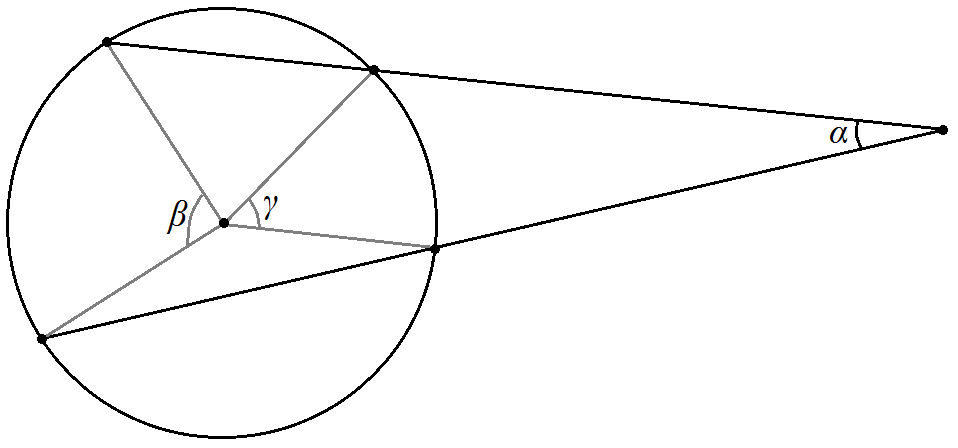
2
Окружность вписана в четырёхугольник (условие, когда это возможно):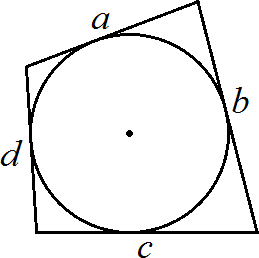
a + c = b + d
Окружность описана около четырехугольника (условие, когда это возможно):
у
С мма углов n-угольника:
α + γ = β + φ = 180
1 2 ... n 180 (n 2) (n 2) рад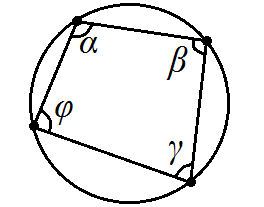
ентрал
Ц ьный угол правильного n-угольника:
360 2
n n
рад
Площадь правильного многоугольника (an – сторона правильного n-угольника, r – радиус вписанной окружности):
S n an r
2
Длина окружности (здесь и далее R – радиус окружности или круга):
L = 2πR
Длина дуги окружности:
Площадь круга:
Площадь кругового сектора:
Lдуги =
Rград
180
S = πR²
= αрад R
Sсектора
= R² град
360
= рад R²
2
Площадь кольца (R – радиус внешней окружности, r – радиус внутренней окружности):
S R2 r2
Площадь кругового сегмента ( 0 ; – угол в радианах):
R2
S sin 2
| 
Скачать 449.79 Kb.