Репетитор по физике и математике Волович Виктор Валентинович Математика

• Название: Репетитор по физике и математике Волович Виктор Валентинович Математика
• Дата: 10.08.2018
• Размер: 449.79 Kb.
• Имя файла: FormMat.docx
• Тип: Документы; #49074
• страница: 7 из 9

Планиметрия

Произвольный треугольник (a, b, c – стороны треугольника, r – радиус ^{вписанной окружности, R – радиус описанной окружности, h}a ^{– высота опущенная на сторону a, h}b ^{– высота опущенная на сторону b, h}c ^{– высота опущенная на сторону c, l}a ^{– биссектриса опущенная на сторону a, m}a ^{– медиана} опущенная на сторону a).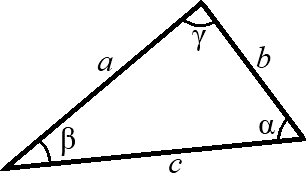

Сумма углов треугольника:

      180  рад

Площадь треугольника через две стороны и угол между ними:

S = ¹ a∙b∙sin γ

2

Площадь треугольника через основание и высоту опущенную на это основание:

^{S = 1 b∙h}b

2

Площадь треугольника (формула Герона):

p( p a)( p b)( p c)

S 


где:

_p a b c

2

– полупериметр. Площадь треугольника через радиус описанной окружности:

_{S } abc

4R

Формула медианы: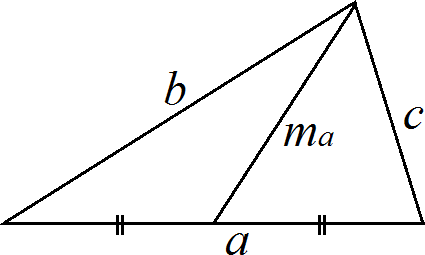

1

2

2(b²  c² )  a²

Свойство биссектрисы:

m_a 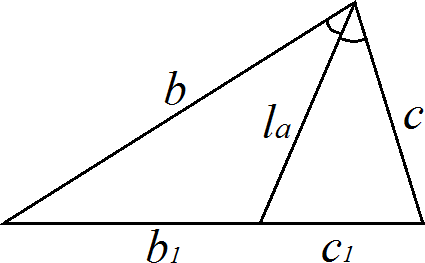

с

о

Ф рмулы биссектрисы:

b _ b₁ c c₁


bc b₁c₁

l_a 

l_a 

cb(b c a)(b c a) c  b


О новное свойство высот треугольника:

h_{a } h_b

b a

Формулы высоты: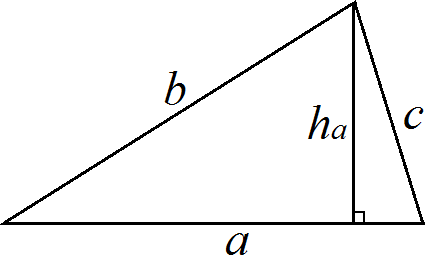

h_a 
2

a

p( p a)( p b)( p c)

1 _ 1 _ 1 _ 1



Теорема косинусов:

h_a h_b h_c r

a² = b² + c² – 2bc∙cos α

Теорема синусов:

a

sin

_ b

sin 

_ c

sin 

 2R

Правильный треугольник (все стороны равны а). Радиус окружности, вписанной в правильный треугольник:

a 3

6

r 

a 3

3

Радиус окружности, описанной около правильного треугольника:

R 

_a2

3

Площадь правильного треугольника:

S 

4

Прямоугольный треугольник (a, b – катеты, с – гипотенуза). Теорема Пифагора:

с² = a² + b² Радиус окружности, вписанной в прямоугольный треугольник:

_{r } a  b  c

2

Радиус окружности, описанной около прямоугольного треугольника:

R  ^c

2


Площадь прямоугольного треугольника:

S  ¹ ab  ¹ hc

2 2

Свойства высоты, опущенной на гипотенузу прямоугольного треугольника: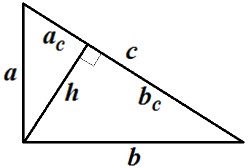



рапец

h²  a b

c c


c

a²  a  c


c

b²  b  c

Т ия (a, b – основания, h – высота). Средняя линия трапеции:

_{l } a  b

2

Площадь трапеции:

S  l  h  ^{a  b}  h

2

Параллелограмм. Площадь параллелограмма через сторону и высоту опущенную на неё:

S = bh

Площадь параллелограмма через две смежные стороны и угол между ними:

S = ab∙sin γ

Квадрат. Площадь квадрата через сторону: Площадь квадрата через диагональ:
S = a²
S  ¹ d ²

2

^{Площадь ромба через две диагонали d}1 ^{и d}2^{, а также через угол между равными сторонами а:}

S  ¹ d d
 a² sin 

₂ 1 2

Площадь прямоугольника через две смежные стороны:

S = ab