Задачи - РГР Математика. Решение задачи принятия решения в условиях неопределенности

• Название: Решение задачи принятия решения в условиях неопределенности
• Дата: 18.06.2022
• Размер: 274.75 Kb.
• Имя файла: Задачи - РГР Математика.docx
• Тип: Задача; #601999
• страница: 8 из 8

Определение исходного опорного плана. Первый опорный план может быть найден посредством различных способов: по правилу северо-западного угла, приоритету ближайших пунктов, способу минимального элемента С=(cij), способу Фогеля и по способу Лебедева-Тихомирова.
1. Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи.

	1	2	3	4	Запасы
1	1[4]	2[2]	4	3	6
2	4	3[4]	8[4]	5	8
3	2	7	6[2]	3[8]	10
4	0	0	0[2]	0	2
Потребности	4	6	8	8

Задача № 2. На автомойке одновременно обслуживается один автомобиль. Чтобы сократить количество отказов существует возможность арендовать места для стоянки транспорта в ожидании обслуживания. Определить оптимальное количество мест для стоянки. Интенсивность обслуживания на мойке 5,1 Интенсивность потока автомобилей на мойку 6,1 Стоимость аренды одного места 5,5 Недополученная прибыль из-за отказа в обслуживании 38,0.
1. Интенсивность нагрузки.
ρ = λ • t_обс = 0.6 • 3.5 = 2.1
Интенсивность нагрузки ρ=2.1 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания.
Поскольку 2.1<5, то процесс обслуживания будет стабилен.
3. Вероятность, что канал свободен (доля времени простоя каналов).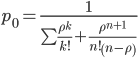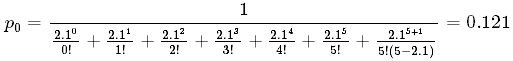



Следовательно, 12.1% в течение часа канал будет не занят, время простоя равно t_пр = 7.3 мин.
4. Вероятность отказа (Доля заявок, получивших отказ).
Поскольку отказ в обслуживании в таких системах не может быть, то p_отк = 0
5. Вероятность обслуживания поступающих заявок (вероятность того, что клиент будет обслужен).
Относительная пропускная способность: Q = p_обс = 1.
6. Среднее число каналов, занятых обслуживанием (Среднее число занятых каналов).
n_з = ρ = 2.1 канала.
Среднее число простаивающих каналов.
n_пр = n - n_з = 5 - 2.1 = 2.9 канала.
7. Коэффициент занятости каналов обслуживанием.

Следовательно, система на 40% занята обслуживанием.
8. Абсолютная пропускная способность (Интенсивность выходящего потока обслуженных заявок).
A = λ = 0.6 заявок/мин.
9. Среднее время простоя СМО.
t_пр = p_отк • t_обс = 0 • 3.5 = 0 мин.
Вероятность образования очереди.


Вероятность отсутствия очереди.
p = 1 - p_оч = 1 - 0.0299 = 0.97
Вероятность того, что придется ждать начала обслуживания равна вероятности того, что все каналы заняты:

10. Среднее число заявок, находящихся в очереди.


11. Среднее время простоя СМО (среднее время ожидания обслуживания заявки в очереди).

12. Среднее число обслуживаемых заявок.
L_об = ρ = 2.1
13. Среднее число заявок в системе.
L_CMO = L_оч + L_обс = 0.0515 + 2.1 = 2.152 ед.
14. Среднее время пребывания заявки в СМО.

Число заявок, получивших отказ в течение часа: λ • p₁ = 0 заявок в мин.
Номинальная производительность СМО: 5 / 3.5 = 1.429 заявок в мин.
Фактическая производительность СМО: 0.6 / 1.429 = 42% от номинальной производительности.