Задачи - РГР Математика. Решение задачи принятия решения в условиях неопределенности
 Скачать 274.75 Kb.
|
|
Продолжительность минимального пути: 34 Задача. Используя исходные данные (слева) рассчитать следующие характеристики для систем управления запасами (справа). Вариант № 29 Рассмотрим плановый период работы предприятия, состоящий из 2-х месяцев. Исходные данные сведены в таблице.
Уровень запасов на начало первого периода равен 0 ед., на конец периода равен 0 ед. Этап I. Условная оптимизация. Рассмотрим первый шаг (k=1). Поскольку плановый период состоит из одного месяца, у нас практически нет возможности влиять на объем производства изделий. Поэтому все допустимые программы выпуска продукции будут оптимальны, поскольку они единственны. Функция состояния примет вид: F1(e)=f1(x1=e-y0+d1, y1=e)=f1(x1=e-0+1) = f1(x1=e+1) Укажем ограничения на изменения переменных x1 и y1. x1 ≤ min(N1, d1+d2+0-0) = min(0, 1) = 0 0 ≤ y1 ≤ min(M1, d2+0) = min(6, 0) = 0 Результаты вычислений сведем в таблицу. k=1, d1=1, g1=8, c1=0, h1=0, L1=0 Таблица 1.
Рассмотрим k = 2. Рекуррентное соотношение примет вид: F2=min(f2(x2, y2)+F1(e-x2+d2)) где e – оптимальное значение уровня запасов y2 на конец 2-го шага, которому соответствует наименьшие суммарные затраты на производство и хранение продукции. Ограничения на объем производства и уровень хранения: x2 ≤ min(N2, d2+0) = min(0, 0) = 0 0 ≤ y2 ≤ min(M2, 0) = min(0, 0) = 0 k=2, d2=0, g2=0, c2=0, h2=0, L2=0 Таблица 2.
Поясним содержание этой таблицы. Объем производства и уровень хранения определяются значениями x2 и y2 соответственно. В квадратных скобках каждой клетки указаны уровни запасов на начало 2 шага, которые с помощью балансового уравнения вычисляются по формуле y1=y2-x2+d2 = y2-x2+0. Сумма внутри каждой клетки содержит три слагаемых. Аналогично рассчитываются слагаемые в остальных клетках, а в «запрещенных» клетках, для которых не нашлось последнего слагаемого в таблице 1 (k = 1) таблице, сделан прочерк. Наименьшие суммарные затраты для каждого y2 запишем в последнем столбце, а значения оптимальных объемов производства изделий занесем в предпоследний столбец таблицы. Этап II. Безусловная оптимизация. Составим оптимальную программу выпуска продукции на каждом этапе, которая обеспечит минимальные суммарные затраты F2(e)=- в течение всего планового периода. Как видно из таблицы N2, x2(e=y2=0)=0, что соответствует оптимальному уровню запасов y1=0, который рассчитан и записан в квадратных скобках. Как видно из таблицы N1, x1(e=y1=0)=0, что соответствует оптимальному уровню запасов y0=0, который рассчитан и записан в квадратных скобках. Таким образом, построена оптимальная программа выпуска продукции: X=0,0, которая обеспечивает минимальные суммарные издержки F2(e)=- на производство и хранение продукции. Задание по данным в таблице дугам составить неориентированный граф. Рассчитать с помощью методов Дийкстра и Беллмана-Форда кратчайшие расстояния от вершины А. Задача № 29 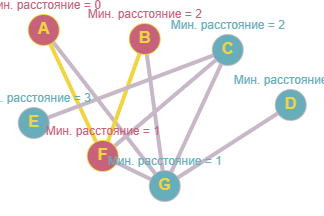 Задача. Составить такой план выпуска продукции, при котором прибыль предприятия будет максимальной. Решить графическим способом, определить какое изменение в прибыли от реализации одного изделия не изменит решение задачи. Предположим, что предприятие изготовит x1изделий вида А и 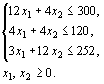 изделий вида В. Поскольку производство продукции ограничено имеющимся в распоряжении предприятия сырьем каждого вида и количество изготовляемых изделий не может быть отрицательным, должны выполняться неравенства Общая прибыль от реализации x1 изделий вида А и изделий вида В составит  Таким образом, мы приходим к следующей математической задаче: среди всех неотрицательных решений данной системы линейных неравенств требуется найти такое, при котором функция F принимает максимальное значение. Найдем решение сформулированной задачи, используя ее геометрическую интерпретацию. Сначала определим многоугольник решений. Для этого в неравенствах системы ограничений и условиях неотрицательности переменных знаки неравенств заменим на знаки точных равенств и найдем соответствующие прямые: 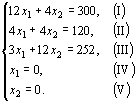 Эти прямые изображены на рис. 5. Каждая из построенных прямых делит плоскость на две полуплоскости. Координаты точек одной полуплоскости удовлетворяют исходному неравенству, а другой – нет. Чтобы определить искомую полуплоскость, нужно взять какую-нибудь точку, принадлежащую одной из полуплоскостей, и проверить, удовлетворяют ли ее координаты данному неравенству. Если координаты взятой точки удовлетворяют данному неравенству, то искомой является та полуплоскость, которой принадлежит эта точка, в противном случае – другая полуплоскость. 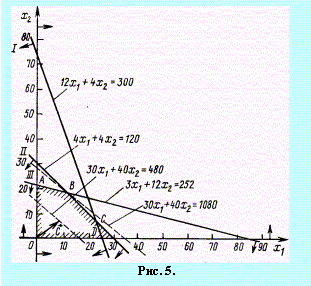 Найдем, например, полуплоскость, определяемую неравенством  Для этого, построив прямую  (на рис. 5 эта прямая I), возьмем какую-нибудь точку, принадлежащую одной из двух полученных полуплоскостей, например точку О(0; 0). Координаты этой точки удовлетворяют неравенству  значит, полуплоскость, которой принадлежит точка О(0; 0), определяется неравенством  Это и показано стрелками на рис. 5.Пересечение полученных полуплоскостей и определяет многоугольник решений данной задачи. Как видно из рис. 5, многоугольником решений является пятиугольник OABCD. Координаты любой точки, принадлежащей этому пятиугольнику, удовлетворяют данной системе неравенств и условию неотрицательности переменных. Поэтому сформулированная задача будет решена, если мы сможем найти точку, принадлежащую пятиугольнику OABCD, в которой функция F принимает максимальное значение. Чтобы найти указанную точку, построим вектор  и прямую  где h – некоторая постоянная такая, что прямая  имеет общие точки с многоугольником решений. Положим, например, h = 480 и построим прямую  (рис. 5).Если теперь взять какую-нибудь точку, принадлежащую построенной прямой и многоугольнику решений, то ее координаты определяют такой план производства изделий А и В, при котором прибыль от их реализации равна 480 руб. Далее, полагая h равным некоторому числу, большему чем 480, мы будем получать различные параллельные прямые. Если они имеют общие точки с многоугольником решений, то эти точки определяют планы производства изделий А и В, при которых прибыль от их реализации превзойдет 480 руб. Перемещая построенную прямую в направлении вектора  видим, что последней общей точкой ее с многоугольником решений задачи служит точка В. Координаты этой точки и определяют план выпуска изделий А и В, при котором прибыль от их реализации является максимальной.Найдем координаты точки В как точки пересечения прямых II и III. Следовательно, ее координаты удовлетворяют уравнениям этих прямых  Решив эту систему уравнений, получим  Следовательно, если предприятие изготовит 12 изделий вида А и 18 изделий вида В, то оно получит максимальную прибыль, равную  Задача № 1. На склад под погрузку и разгрузку поступает поток транспорта. Вследствие возникновения очереди транспортные средства несут убытки. С другой стороны, каждое дополнительное погрузочное устройство несет дополнительные затраты для склада. Найти оптимальное количество погрузочных устройств, минимизируещее суммарные потери склада и транспорта в логистической цепи при следующих характеристиках системы: Проверим необходимое и достаточное условие разрешимости задачи. ∑ a = 6 + 8 + 10 = 24 ∑ b = 4 + 6 + 8 + 8 = 26 Как видно, суммарная потребность груза в пунктах назначения меньше запасов груза на базах. Следовательно, модель исходной транспортной задачи является открытой. Чтобы получить закрытую модель, введем дополнительную (фиктивную) потребность, равным 2 (26—24). Тарифы перевозки единицы груза из базы во все магазины полагаем равны нулю. Занесем исходные данные в распределительную таблицу.
Первая итерация заключается в определении исходного опорного плана и проверке его на оптимальность. |