Решить интегральное уравнение значит найти такую функцию, которая

• Название: Решить интегральное уравнение значит найти такую функцию, которая
• Дата: 18.11.2022
• Размер: 445.79 Kb.
• Имя файла: 1.docx
• Тип: Документы; #797302
• страница: 8 из 8

2

  

^  _  _ 1 ^;



C

1


^  _1 
_ 3 <sub>

2 </sub>C₂   ₂

D  

1  ^ ;

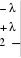2

^ ; 1
_2

 1  . 12

3

Это интегральное уравнение всегда имеет действительных .
решение, так как D0 всегда при

12

1

2
^C 12  ^{2 ;}

C  

6   _;

12  ²

 t 

622t 

.

12  ²

Резольвента таких уравнений всегда дробно-рациональная функция.
Использование вырожденных ядер для приблизительного решения интегральных уравнений
Пусть имеем некоторое интегральное уравнение, у которого ядро k(t,S)- вырожденное.

_b

 t   _ kt, S SdS

a

ft.

На интервале интегрирования не вырожденное ядро заменяют вырожденным приблизительным. При этом решение получается достаточно близким к истинному решению. Чем ближе приближение, тем точнее решение.
Используются различные аппроксимации. Проще всего заменять суммой или тригонометрическими функциями.

Пример.

 t  _ t1  e^tS SdS


1
0

• 
  e^t
  

• 
  t.
  

Точное решение  t  1.

k_b
t, S
 t
² S
_t3 _S2

2

_t4 _S3

 ;

6

 t  e^t

 t 0,5t²

 0,17t³  0,04t⁴ .

На интервале [0;1] отклонение от точного решения составляет всего 0,8%.

Заключение

Теория интегральных уравнений — обширная область математики, которая имеет приложения в самых разных областях. Интегральным уравнениям посвящены десятки превосходных книг и учебников. Настоящие краткие заметки не могут и не должны заменять собой полноценный учебник и предназначены лишь для первого знакомства с основными понятиями. В связи с этим используется минимум терминологии из функционального анализа. Оборотной стороной такого подхода является не самая общая формулировка некоторых теорем и необходимость опустить некоторые доказательства. Что касается краевых задач, то они являются одним из приложений теории интегральных уравнений и непосредственно примыкают к рассмотренному кругу вопросов.

Определение: Интегральными уравнениями называются уравнения, содержащие неизвестную функцию под знаком интеграла.

Многие задачи математической физики сводятся к линейным интегральным уравнениям.

Определение: Интегральное уравнение называется линейным, если в него неизвестная функция входит линейно.

Решить интегральное уравнение – значит найти такую функцию, которая обращает данное уравнение в верное тождество.

Интегральные уравнения подразделяются на уравнения первого рода и уравнения второго рода. В уравнения первого рода неизвестная функция входит только под знаком интеграла. В уравнения второго неизвестная функция входит как под знаком интеграла, так и вне интеграла.

Уравнения первого и второго рода с постоянными пределами интегрирования называются уравнениями Фредгольма, а уравнения с переменным верхним пределом называются уравнениями Вольтерра.

Список литературы

1. 
   А.Н.Тихонов, А.Б.Васильева, А.Г.Свешников, Дифференциальные уравнения, М., Наука, 1979
   
2. 
   Бахвалов Н. С., Панасенко Г. П. Осредненние процессов в периодических средах. М.: Наука, 1984. 352 с.
   
3. 
   Боголюбов Н. H., Митропольский Ю. А. Асимптотические методы в теории нелинейных колебаний. М.: Наука, 1974. 504 с.
   
4. 
   И.Г.Петровский, Лекции по теории интегральных уравнений, М., Наука, 1965
   
5. 
   Камке Э. Справочник по обыкновенным дифференциальным уравнениям. М.: Наука, 1971. 576 с.
   
6. 
   Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа. М.: Наука, 1972. 496 с.
   
7. 
   Корн. Г., Корн Т. Справочник по математике для научных работников и инженеров. – М.: Наука, 2007.
   
8. 
   Краснов М. Л., Киселев А.И., Макаренко Г.И. Интегральные уравнения. Задачи и решения. – М.: Наука,2006.
   
9. 
   Краснов М.Л. Интегральные уравнения (Введение в теорию)/Главная редакция физико-математической литературы. – М.: Наука,2005.
   
10. 
    Л.Я.Цлаф, Вариационное исчисление и интегральные уравнения, М., Наука, 1970
    
11. 
    Лионс Жак-Луи. Некоторые методы решения нелинейных краевых задач: Пер. с фр. Под ред. и с предисл. О.А. Олейник. Изд. 3-е. М.: Едиториал, 2010. 586 с.
    
12. 
    Ломакин В. А. Теория упругости неоднородных тел. М.: Изд-во МГУ, 1976. 367 с.
    
13. 
    М.В.Федорюк, Обыкновенные дифференциальные уравнения, М., Наука, 1980
    
14. 
    М.Л.Краснов, А.И.Киселев, Г.И.Макаренко, Интегральные уравнения ( задачи и упражнения ), М., Наука, 1968
    
15. 
    М.Л.Краснов, Интегральные уравнения, М., Наука, 1975
    
16. 
    Маделунг Э. Математический аппарат физики – М.: Наука, 2008.
    
17. 
    Найфе А. Х. Методы возмущений. М.: Мир, 1976. 456 с.
    
18. 
    П.И.Лизоркин. Курс дифференциальных и интегральных уравнений с дополнительными главами анализа, М., Наука, 1981
    
19. 
    Победря Б. Е. Механика композиционных материалов. М.: Изд-во МГУ, 1984. 336 с.
    
20. 
    Полушин П.А., Архипов Е.А. Интегральные уравнения. Краткий курс лекций для магистров по направлению 552500. – Владимир, ВлГУ, 2003.
    
21. 
    Степанов В. В. Курс дифференциальных уравнений. М.: Государственное издательство физико-математической литературы, 1958. 468 с.
    
22. 
    Суетин П. К. Классические ортогональные многочлены. М.: Наука: главная редакция физико-математической литературы, 1979. 416 c.