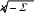Решить интегральное уравнение значит найти такую функцию, которая

• Название: Решить интегральное уравнение значит найти такую функцию, которая
• Дата: 18.11.2022
• Размер: 445.79 Kb.
• Имя файла: 1.docx
• Тип: Документы; #797302
• страница: 1 из 8

_{Введение}

Одним из наиболее важных условий прогресса в области решения различных исследовательских задач является освоение и внедрение в практику прикладных разделов современной математики. К этим разделам, прежде всего, относятся приближенные, численные и машинные методы решения интегральных уравнений, применение которых позволяет получить эффективные математические описания многих прикладных задач. Интегральными уравнениями называются такие функциональные уравнения, которые содержат интегральное преобразование над искомой функцией. Аппарат интегральных уравнений широко используется в физике, механике, теории управления и в прикладной математике.

Уравнение называется интегральным, если неизвестная функция входит в уравнение под знаком интеграла. Разумеется, мы не будем рассматривать интегральные уравнения в такой общей постановке, а ограничимся изучением только одномерных линейных интегральных уравнений следующих типов.

Решить интегральное уравнение – значит найти такую функцию, которая

обращает данное уравнение в верное тождество.

Интегральные уравнения подразделяются на уравнения первого рода и уравнения второго рода. В уравнения первого рода неизвестная функция входит только под знаком интеграла. В уравнения второго неизвестная функция входит как под знаком интеграла, так и вне интеграла.

Уравнения первого и второго рода с постоянными пределами интегрирования называются уравнениями Фредгольма, а уравнения с переменным верхним пределом называются уравнениями Вольтерра.

В данной работе будем рассматривать линейные интегральные уравнения двух типов:

- уравнение Фредгольма,

- уравнение Вольтерра (частный случай уравнения Фредгольма).

Уравнения Вольтерра более просты, чем уравнения Фредгольма; уравнения второго рода более просты, чем уравнения первого рода. Уравнение Вольтерра можно при некоторых ограничениях рассматривать как частный случай уравнения Фредгольма.

1. Понятие интегрального уравнения. Основные методы решения интегральных уравнений

Интегральное уравнение - уравнение, где неизвестная функция входит под знак интеграла.
Линейные интегральные уравнения
Условимся, что

f(t) - известная функция.

 (t) - неизвестная искомая функция.
Интегральное уравнение называется линейным, если неизвестная функция, входящая в него, линейна.

Классическая запись линейного интегрального уравнения:

b

 (t)   _ k(t, S) (S)dS f(t) ,

a

где  - параметр, задающий семейство решений интегральных уравнений;

k(t, S) - ядро интегрального уравнения.

Функция f(t)

существует в пределах

a t b^.

Функция

k(t, S)

существует в пределах

_a t b



^a S b^.

Общий вид интегрального уравнения Фредгольма 1-го рода

b

_ k(t, S) (S)dS

a

f(t)
- интегральное уравнение Фредгольма 1-го рода.

b

 (t)   _ k(t, S) (S)dS

a

f(t) - интегральное уравнение Фредгольма 2-го

рода.

аи bмогут быть конечными или бесконечными. Условия существования решений уравнений:

f(t)- непрерывна на интервале a,b.

b

_ f(t)

a

2 dt +  .

k(t, S)

- непрерывна в интервалах

_a t b



^a S b^;

Если ядра удовлетворяют вышеприведенным условиям, то ядра называются

фредгольмовыми. Если однородным:

f(t)  0 , то такое интегральное уравнение называется
b

0   (t)   _ k(t, S) (S)dS.

a

Интегральные уравнения Вольтерра

1. 
   1-го рода
   

2. 
   2-го рода
   

t

_ k(t, S) (S)dS

a
f(t) .

t

 (t)   _ k(t, S) (S)dS

a

f(t) .

Если

f(t)  0 , то уравнение называется однородным. При определенных

ограничениях, уравнения Вольтерра упрощенно рассматривают уравнениями Фредгольма. Если модифицировать ядра следующим образом

_k(t, S), S t_

0


H(t, S)  _



, S t^{ ,}

то мы придем к записи интегрального уравнения

b

 (t)   _ H(t, S) (S)dS

a
f(t) .

2. Классификация интегральных уравнений. Линейные и нелинейные интегральные уравнения. Уравнения Фредгольма и Вольтерра. Важные типы нелинейных интегральных уравнений. Примеры.

Виды нелинейных интегральных уравнений

1. 
   Интегральное уравнение Урысона
   

b
 (t)  _ kt, S, (S)dS.

a

Если неизвестная функция входит внутрь ядра, то такие уравнения называются уравнениями Урысона.

2. 
   Уравнение Гаммерштейна
   

b

где

k(t, S)

 (t)  _ k(t, S)FS, (S)dS,

a

- обычное фредгольмовое ядро.

3. 
   Уравнения Ляпунова - Лихтенштейна.
   

Они включают в себя существенно нелинейные функции.

 (t) 

b

f(t)   _ k₁ (t, S) (S)dS

a

bb

  _{ } k₂ (t, S, z) (S) ( z)dSdz.

aa

4. 
   Нелинейные интегральные уравнения Вольтерра.
   

t
 (t)  _ kt, S, (S)dS.

a
Примеры.

₁ 

1. g( x) 

_ ejxy f( y)dy.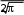



Это интегральное уравнение Фредгольма 1-го рода.

_ei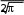xy

k( x, y)  .

Решение его имеет вид:
 ( y) 
₁ 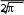

_ eixy g( x)dx.



2. 
   dx(t)
   

dt

 F[t, x(t)] .

Проинтегрируем обе части этого выражения по t:

t


x
x(t)   F[t, x(t)]dt;

0 ^

a


0
x(a)  x.

2. 
   Общая задача решения линейного дифференциального уравнения n-го порядка.
   

dn x



1

n
dtn

• 
  a(t)
  

_dn1 <sub>x


dt</sub>n1

 ...  a

(t) x(t)  F(t) ^;

0
x(a)  c;


1
x^' (a)  c;

. . .

n1
x^{( n1)} (a)  c .

d² x

Рассмотрим n=2:

dx

dt²

 at

1
dt
 atxt  Ft ;

2
d² x


dt²

  t ;

dx_

dt

_t

_  SdS

0

• 
  C ;
  

1
t t t

t


1
n1

_ dt_ dt… _ ftdt _{n 1! } t S

fSdS;

0 0 0 0

t

1 0
xt  _ t S SdS

0

• 
  Ct C.
  

Подставим в исходное дифференциальное уравнение:

t

1 1 1 2 0 2
 t  _ a₁ t  a₂ tt S SdS

0

Обозначим

 Ft  Cat  Ctat  Cat.

1

2
kt, S  a

t  att S ;

1

1

0

2
ft  Ft  Ca

t  Cta

t  Ca

t ;

1

2
Интегральное уравнение Вольтера 2-го рода

_t

 t  _ kt, S S 

0
ft.

Во многих случаях ядро k(t,S)=k(t-S) (пропорционально разности аргументов),

тогда уравнение Вольтера называется интегральным уравнением типа свертки. Интегральное уравнение Абеля:


_{fx } ^x S

0

dS.

Если неизвестная функция входит и под знак производной и под знак интеграла, то такое уравнение называется интегро-дифференциальное (ИДУ).

3. Теория Фредгольма для решения интегральных уравнений общего вида.

Резольвента, ее построение и использование. Интегральные уравнения с вырожденным ядром

Методы Фредгольма
В начале века Фредгольм наиболее полно исследовал интегро- дифференциальные уравнения.

_b

 t   _ kt, S S 

a

ft.

Решение этого уравнения рассматривается как аналог решения системы n линейных алгебраических уравнений с n неизвестными. В результате решение получается приблизительным, зависящим от n. Чем больше n, тем больше приближение.

Решение состоит из нескольких этапов:

1. 
   Интеграл заменяется конечной суммой.
   

2. 
   Весь отрезок [a,b] разбивается на n равных частей 
   

_ b a_.

n

3. 
   
   j
   
   
   
   j
   Внутри каждого интервала jвыбирается некоторая точка S_j. Получаем набор функций (S_j)=_j. Ищем не непрерывную функцию, а набор дискретов S_j.
   

 t  

n