химия. Российская академия образования институт содержания и методов обучения

• Название: Российская академия образования институт содержания и методов обучения
• Анкор: химия
• Дата: 08.10.2022
• Размер: 0.77 Mb.
• Имя файла: dis1_chi.doc
• Тип: Диссертация; #722092
• страница: 5 из 11

Глава 2. Педагогико-эргономические требования к созданию и использованию моделей для изучения строения вещества.
2.1. Принцип научности и адаптация новых научных данных для обучения. Современные тенденции развития моделирования.
Среди основных принципов целостного педагогического процесса принцип научности обучения является важнейшим. В свою очередь, принцип доступности требует, чтобы обучение строилось на уровне возможностей учеников. При слишком усложненном содержании понижается мотивационный настрой, резко падает работоспособность. Вместе с тем при упрощенном содержании снижается интерес к учению, то есть упрощение содержания обучения снижает его развивающее влияние [83, с.47-48]. Выдающийся химик и методист А. М. Бутлеров постоянно подчеркивал, что на всех этапах обучения независимо от учебного заведения излагаемые знания должны быть доступны учащимся. Как отмечал И. Н. Чертков, рассматривая значение работ А. М. Бутлерова для развития методики обучения химии [131, с.17], иногда учителя слишком усложняют учебную программу, считая необходимым знакомить учащихся с теориями, понятиями, которые недоступны им (теория резонанса, молекулярных орбиталей и др.).

Под научностью подразумевается не только формирование научного подхода к изучаемым явлениям у школьников, но и научная достоверность содержания изучаемого предмета или явления. Модели, используемые в обучении, должны иметь возможность отражения научно установленных фактов.

Как было показано в главе 1, проблемы создания и использования моделей объектов микромира существуют. Поставим прикладной вопрос в общем виде: нужна ли при изучении дисциплин естественнонаучного цикла модель электрона? А если нужна, то какими свойствами она должна обладать? Рассмотрим, как решается этот вопрос в научном сообществе.

В смежных с физикой областях - в химии, в кристаллографии в качестве наглядных геометрических моделей атомов используют полиэдры (многогранники), или шары, усеченные плоскостями, перпендикулярными линиям связи. Электрон при этом либо не изображается, либо считается облаком, форма которого неопределенная, изменчивая, но должна показывать пространственное распределение плотности вероятности нахождения всего электрона в определенной точке пространства. Строго говоря, определенной наглядной модели электрона просто нет.

Может и вообще не нужна была бы модель электрона, если бы...она уже не использовалась в неявном виде и в квантовой химии, и в квантовой физике. Ведь сам термин "перераспределение электронной плотности" и характеризующие его матрицы электронных плотностей подразумевают некоторую протяженность и изменяемость формы электронов. При этом утверждается, что даже сам термин "форма электрона" является некорректным, так как формы у электрона нет, размер его неопределенно мал, а определение его местоположения принципиально невозможно точнее величины, вычисляемой из соотношения Гейзенберга.

Таким образом, отказ от наглядных геометрических моделей не обоснован уже хотя бы тем, что моделируемые объекты реально существуют, имеют протяженность и определенную плотность. Кроме того, для качественного формирования понятий необходимы именно наглядные геометрические модели, так как образное восприятие - самое информативно насыщенное и помогает усваивать сложный материал. Возможность использования структурных моделей тем более важна, что, как известно, в химии «свойства веществ – функция их строения» [134].

Без наглядной, пусть и упрощенной модели, невозможно работать с объектами микромира. Разнообразные модели все равно используются, но они содержат не только массу недостатков, но и находятся в противоречии с основными законами физики. Но предложить универсальную непротиворечивую модель электрона невозможно, потому что противоречия содержаться в самих представлениях об электроне. То есть для создания непротиворечивой геометрической модели электрона, необходимо избавиться от противоречий в представляемых нами свойствах электрона.

Одно из основных противоречий заключается в том, что электрон представляется частицей безразмерной, но в то же время имеющей моменты вращения и, вообще говоря, определяющей размеры атома [1, 18, 19, 56, 80]. Чтобы избежать этого противоречия, можно вернуться к модели атома, предложенной Шредингером. В ней электронные заряды и токи непрерывно распределены по объему атомной системы с плотностями, выражающимися через волновую функцию. Сам Шредингер считал, что: "Квадрат волновой функции имеет смысл плотности электричества" [136]. Электрон при этом рассматривается в виде непрерывного потока стационарно вращающегося электрического заряда, потоки энергии в котором, замкнуты сами на себя и также стационарны. Возможность использования в квантовой механике представления Шредингера об электроне подробно рассмотрена в работах Власова А. Д. [18, 19]. В работе [19] не только рассматриваются и интерпретируются на языке квантовой механики предположения Шредингера, но и проводится историческое и хронологическое исследование, посвященное причинам отхода квантовой науки от использования представлений Шредингера, единственных, совместимых с классической электродинамикой. Власов А. Д. отмечает, что истолкование Шредингера приводит к динамической модели атома, в которой заряды электронов непрерывно распределены по всему объему атома, и что в связи с этим возникает новое представление об электронах, как о частицах тех же размеров, что и сам атом. При этом стационарно вращающийся электрический заряд электрона, в полном согласии с классической электродинамикой, не излучает электромагнитной энергии - потоки в нем замкнуты сами на себя и также стационарны.

Критическое переосмысление существующих физических теорий приводит к появлению новых теорий или предложений пересмотра старых, ранее отвергнутых научно-общественным мнением. В частности, сейчас существует много теорий - ревизий старой идеи наличия среды - эфира, проводящей электромагнитные волны. В рамках этих теорий электрон может рассматриваться как стационарный многокомпонентный волновой процесс в среде - эфире, характеризующийся резонансными параметрами этого процесса в среде. Отсутствие излучения электрона на орбите пытаются объяснять замкнутостью траектории его циркуляции. Однако, выходя за рамки ортодоксальной науки, (с точки зрения натурфилософии) было бы естественней предположить, что диссипация энергии все же имеет место (хотя бы на излучение волн, поддерживающих структуру поля электрона). Восстановление энергетического баланса и стационарное существование электрона неопределенно долгое время можно объяснить тем, что электрон является процессом в активной среде - эфире. Иначе говоря, можно предположить, что электрон является резонансным волновым процессом в структуре вакуума, или эфира. А его поля представляются различными формами напряженно - деформированных состояний структуры эфира. Эту идею высказывал еще Г. А. Лоренц. Электрон представляется преобразователем внутренней энергии физического или “кипящего” вакуума (или эфира) во внешнюю, то есть в энергию его электрического и магнитного поля. На сегодняшний день такое теоретическое положение можно принять только как аксиому, так как невозможность обнаружения "всемирного эфира" в физических экспериментах есть одно из его свойств (или следствие его наличия).

В течение последних 40 лет разными авторами активно «реанимируется» и развивается гипотеза неувлекаемого эфира. Например, “Теория упругой квантованной среды” В. С. Леонова [59], описывающая элементарную ячейку эфира как электромагнитный квадроуполь планковских размеров и энергий. Планковская длина представляет собой наименьшую длину в однородной области недеформированного пространства, свободного от гравитационного воздействия. Существуют гипотезы увлекаемого эфира, например, “Эфиродинамика” Ацюковского В. А. [6]. Эти исследовательские гипотезы – антагонисты, то есть входить друг с другом в противоречие. Приемлимой для использования могла бы оказаться теория эфира (или вакуума), «увлекаемость» частей которого являлась бы следствием инертности электрических и магнитных полей, оказывающих сопротивление изменениям их структуры.

Однако, даже не рассматривая суть различных теорий, предположений и обоснованность их выдвижения, можно отметить значение моделей в процессе познания и трудности, к которым приводит их отсутствие.

Во второй половине 20 века становится всё больше сторонников старинной модели элементарной частицы в виде кольцевого вихря. Первое упоминание о мельчайшей частице вещества в виде кольцевого вихря было сделано более 5 тысяч лет - это древнее Тибетское знание. Множество авторов в различных вариантах открывают заново эту древнюю модель элементарной частицы и с ее помощью разъясняют устройство атома и процессы микромира, не имеющие удовлетворительного объяснения, или не объясненные вовсе, а лишь задекларированные в рамках существующих физических теорий. Например, моделировать электрон в виде частиц, составляющих массу электрона, вращающихся по кольцу радиусом 0,193 пм предложил Дидык Ю.К. [38]. Электрон в виде "устойчивого вихря" был предложен В.А.Ацюковским [6]. Dave Bergman [1, 2] моделирует элементарные частицы в виде торов, размер которых определяется длиной волны Комптона для моделируемой частицы. Канарев Ф.М. [52] изображает вращающимся кольцом и фотон, и электрон. Спин частиц он интерпретирует как механический момент вращения кольца. Власовым А. Д. [18, 19] была описана модель ротационного атома, предложенная на основе динамической модели атома Шредингера. Беклямишев В. О. [7] предложил электрон изображать тором, окруженным стоячими квантовыми волнами, имеющими на поверхности сферы, окружающей электрон, особые узловые точки, количество которых соответствует числу электронов на различных энергетических уровнях s, p, d, f. Бунин В. А. [13] предложил мыслить частицы объектами, построенными из замкнутых магнитных струн. Его модель электрона в виде вращающейся восьмерки - свернутого “вихревого жгута” - обладает спином, “зарядом”, магнитным моментом.

Модель электрона Ромазанова Б. И. [94] – это ограниченная двумя узловыми поверхностями пучность стоячей сферической волны электрического напряжения. Средой, в которой протекает процесс, является эфир. Ромазанов эфир мыслит не электромагнитным, а чисто электрическим континуумом.

Подобного вида модели электрона обладают новыми возможностями и достоинствами. Но они не универсальны и достаточно сильно отличаются друг от друга, что препятствует их совместимости. Например, модель электрона в виде тора малого размера, полученная расчётным приравниванием скорости движения волны (или распределенного заряда) по кольцу к скорости света ”С”, предполагает движение электронов - торов комптоновского размера по замкнутым траекториям в атоме, что возвращает нас фактически к планетарной модели [38]. Предполагаемое в [1] расположение электронов в атоме в виде тонких торов, объединенных в оболочку на манер одной или нескольких «связок бубликов на веревочке», или в виде отдельных витков соленоида, взаимно не связанных, приводит к трудностям моделирования форм стационарных электронных оболочек, так как не объясняет причины повышенной устойчивости определённых электронных оболочек (устойчивость которых объясняет вид Периодической системы химических элементов Д. И. Менделеева). Модель электрона Канарева Ф. М. [52] в виде жесткого тора, вращающегося вокруг своей оси симметрии, требует мотивированного объяснения синхронного и целочисленного увеличения диаметра электрона и уменьшения частоты его вращения, необходимых для сохранения постоянства его момента вращения (численно равного постоянной Планка) в процессах перехода электрона с уровня на уровень.

Кеннет Снельсон в 1963 году предложил моделировать все электроны в атоме кольцевыми магнитами, изображая тем самым вид электронных оболочек атома любой сложности [4]. Модели К. Снельсона не были востребованы в науке из-за ограниченности применения в отсутствие математического аппарата их использования, который мог бы конкурировать с квантовой механикой.

Большинство из приведённых выше моделей, представляя собой простые и наглядные образы, могли быть использованы в педагогике, но неразработанность методического аппарата их использования привела к тому, что их просто не заметили.

Существуют и более сложные модели, которые трудно адаптировать для использования в школе. Например, профессор Сапогин Л. Г. [100] использует в модели электрона понятие туннелирования: электрон атомной оболочки совершает квантовые скачки в пределах орбитали не беспорядочно, а сквозь ядро атома, каждый раз проходя (туннелируя) через него. Туннелирует электрон благодаря тому, что в это мгновение он находится в «нулевой фазе», при которой мгновенные значения массы и заряда электрона равны нулю. Опираясь на эту гипотезу, Фоминский Л. П. предложил «полуклассическую» модель, в которой «падающий к ядру электрон ускоряется его электрическим полем до околосветовых скоростей. А с увеличением скорости сечение электромагнитных взаимодействий частиц, как известно, уменьшается, и частицы не успевают провзаимодействовать. Так как ядро и сам электрон обладают магнитным моментом, то при пересечении падающим электроном силовых магнитных линий на него действует сила Лоренца, заставляющая электрон отклониться от прямолинейной траектории. В результате падающий к ядру электрон не попадает в центр ядра, а пролетает мимо» [90, с. 218]. В этой модели атома электрон совершает гармонические колебания относительно ядра, как шарик на резинке. Поскольку движения электрона между точками максимального удаления от ядра остаются для наблюдателя незаметными, то создается иллюзия движения электрона по круговой орбите со скоростью С*=С/137.033. Иллюзия движения электрона по круговым и эллиптическим орбитам в атоме не сопровождается излучением электромагнитных волн. Модель Л. П. Фоминского популярно изложена и позволяет совмещать наглядность, свойственную классическим моделям, и квантованность положений электрона в атоме.

На основе проведённого анализа существующих моделей электрона, можно сделать вывод, что сложность предлагаемых мысленных моделей препятствует созданию материальной модели [7, 59, 82, 90, 94, 100]. Кроме того, большинство вышеперечисленных моделей не дают однозначного способа распределения электронов вокруг ядра сложного атома по оболочкам в соответствии с закономерностью, на основе которой построена Периодическая система химических элементов Д. И. Менделеева.

Поэтому предлагается использовать геометрическую модель электрона в виде тонкого тора, размер которого больше комптоновской длины и определяет размер атома [56]. Такой “крупный” электрон может покоиться, то есть пребывать в стационарном состоянии, уравновесив взаимное притяжение с ядром взаимным отталкиванием с другими электронами, окружающими ядро атома. Из этого следует, что модель электрона в виде кольца уже не нуждается в жесткой декларации первого Постулата Бора и не требует возведения соотношения неопределенностей Гейзенберга в принцип, так как электрон представляется системой с распределенными параметрами, характеризующимися известным соотношением В. Гейзенберга.

При геометрическом моделировании элементарной частицы тонким тором, или кольцом, снимается антагонизм корпускулярно-волнового дуализма: кольцо символизирует волновой процесс циркуляции распределенного заряда по замкнутому контуру, что демонстрирует волновую природу частицы, а корпускулярные свойства объясняются ограниченностью процесса в пространстве. Размер кольца, изображающего электрон, зависит от напряженности поля ядра или системы ядер, поэтому является величиной переменной. На внешних оболочках его размеры близки к 1Å (100пм) и определяют валентные размеры атома в соединениях.

Прежде чем переходить непосредственно к описанию закономерностей моделирования электронных конфигураций атомов, молекул и кристаллов с использованием модели электрон - кольцо, следует обратить внимание на то, что модель эта является упрощенной - в ней не отражается внутренняя структура электрона. А для модели электрона, характеризующейся размерами порядка ангстрема (10^-10м) возможность описания внутренней структуры имеет значение.

Известно, что в эффекте Комптона сечение поглощения энергии имеет максимум на длине волны о= h /(mec), что соответствует равенству энергии падающего фотона полной энергии электрона (hо=0,511 Мэв) [54]. Максимальная передача энергии между излучением и электронами, осуществляющаяся при совпадении энергии фотона с полной энергией электрона означает, что максимуму передачи энергии соответствует равенство длины волны падающего излучения о комптоновской длине волны электрона. Опираясь на этот результат, по аналогии с классическим эффектом резонанса, можно предположить, что внутренняя структура электрона связана с комптоновской длиной. Поскольку предполагается, что электрон - это многокомпонентный волновой процесс, то одной из его компонент может быть распространение фронта волны комптоновской длины по кольцу. Это движение можно представить в виде смещения в кольце узлов и пучностей комптоновских волн. Объясняется это движение тем, что по периметру кольца укладывается нецелое число волн. Число волн комптоновской длины, укладывающихся в периметре тора равно величине, обратной так называемой постоянной тонкой структуры – «» (1/ =137.036). Величина «» (постоянная тонкой структуры) определена в экспериментах и является постоянным коэффициентом, встречающимся в расчетах. Движение каждого узла волны комптоновской длины можно рассматривать как распространение фронта электронной волны по замкнутой траектории. Таким образом, предлагаемая модель электрона позволяет рассматривать спин как момент, возникающий в результате циркуляции по кольцу узлов и пучностей электронной волны, продвижение которых вполне может соответствовать движению в контуре (в частном случае в кольце) распределенного заряда, суммарно равному элементарному.

Математически спин как момент, возникающий в результате циркуляции потока энергии, или распространения фронта волны по замкнутому контуру уже рассматривался [80]. Наличие у электрона, моделируемого кольцом (или другим замкнутым контуром), магнитного момента позволяет использовать в качестве материальной модели кольцо с током. Но предпочтительнее использовать не кольцо (тор), а гибкие замкнутые контуры с током. С их помощью можно демонстрировать и принцип неопределенности. Если аналогом электрона является контур с током, то аналогом процесса обнаружения электрона является разряд в точке контакта с этим контуром. До тех пор, пока искровой разряд не произошел, положение электрона точно не определено. Но искровой разряд (аналог процесса поглощения, то есть обнаружения электрона) может произойти в любой точке контура с током. Если и далее прослеживать эту аналогию, то надо заметить, что форма проводника может быть различной, в зависимости от накладываемых на него внешних взаимодействий, но не произвольной, а стремящейся к наиболее лаконичной форме, например, к кольцу с целью минимизации потерь магнитным полем этого проводника.

Для моделирования только магнитной составляющей поля электрона можно использовать кольцевые магниты. Использование магнитных колец позволяет моделировать взаимодействие электронов в оболочках. У модели электрона в виде магнитного кольца будет два варианта расположения в кольцегранной оболочке: северным или южным полюсом к ядру. Вектор, соединяющий N (северный полюс) и S (южный полюс), совпадает с вектором спин. Этот вектор направлен по нормали к кольцу. Наличие у электрона магнитных свойств является причиной образования в атоме нескольких особенно устойчивых электронных оболочек. Модели устойчивых оболочек представляют собой наиболее симметричные фигуры из колец, в которых соприкасающиеся кольца-электроны характеризуются различными знаками спин. На моделях они показаны кольцами разного цвета. Метод геометрического моделирования электронных оболочек в виде кольцегранников позволяет наглядно демонстрировать повышенную устойчивость электронных оболочек из 2, 8, 18 и 32 электронов. Также с помощью новой модели можно объяснить наличие у электрона в атоме орбитального момента - это момент, возникающий из-за несовпадения центра электрона - кольца с геометрическим центром оболочки, в котором находится ядро атома. Математическая процедура разделения момента импульса на две независимые части, первая из которых описывает орбитальный момент, а вторая – спин, приведена в статье: «Что такое спин?» [80, с. 75].

Модель электрона в виде поляризованной по кругу волны комптоновской длины, фронт которой распространяется по кольцу, равному радиусу первой орбиты Бора (0.529 Å) не является полным определением электрона, а лишь характеризует одну из компонент волнового процесса, составляющего электрон.

Так как колебательные процессы с существенно различающимися длинами волн почти не взаимодействуют между собой, то вторичной структурой электрона (относительно волн Комптона) может быть наличие в кольце стоячих волн. В электронном кольце их укладывается целое число, что может демонстрировать целочисленность главного квантового числа «n». В частности геометрические модели электронных оболочек позволяют подсчитать число точек контакта колец в кольцегранниках, которое должно быть равно или кратно числу узлов в колеблющихся кольцах - электронах.

Такая модель имеет возможность описания квантовых переходов. Под этим подразумевается не бесконечно быстрый процесс перескакивания электрона, а процесс перехода электронного окружения атома из одной формы колебаний в другую. Например, изменение суммарного числа стоячих волн, уложенных в кольцевых электронах какой-либо фиксированной оболочки, будет сопровождаться изменением энергетического состояния всего атома и определенным образом должно зависеть от этих целочисленных величин. Как отмечал Шредингер, "изменение форм колебаний всегда может происходить непрерывно в пространстве и времени, оно может длиться время, равное экспериментально определенному времени излучения" [136].

Электрон проявляет себя как многокомпонентный волновой процесс, каждая из компонент которого может (а с дидактической точки зрения и должна) быть отображена соответствующим образом. Как отмечала Михайлова И. Б. «в том случае, когда у нас есть образ интересующей нас стороны объекта, модель попросту не нужна» [71]. Если образа нет, то его следует создать с помощью модели, или образа-модели. Образ-модель отличен от образа непосредственного живого созерцания тем, что это условный образ. Роль образа-модели в формировании комплекса моделей и последовательность его формирования показана на схеме 2.1.

Значительной дидактической функцией обучающих моделей является адаптивность к уровню знаний обучаемого. То есть сложность модели должна соответствовать не сложности моделей «переднего края науки», а уровню знаний субъекта обучения, должна соответствовать познавательным возможностям учащихся, их подготовке и возрастным особенностям. В этом случае простота восприятия напрямую связана с неминуемой популяризацией и упрощением учебного материала. Конечно, упрощение не должно происходить в ущерб научности, то есть адаптивность модели не должна входить в противоречие с её информативностью.

Схема 2. 1.
Формирование комплекса моделей















Отбор информации для обучения

Демонстрацион-ный химический эксперимент





Популяризация сведений об объекте

Ученический эксперимент






Разделение по доминантным признакам.

Проектирование моделей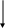


В современном информационно-насыщенном мире быстро меняются условия обучения: увеличивается суммарный объем изучаемого материала, сокращается количество часов, посвященных изучению естественнонаучных дисциплин, в частности и физики, и химии. В соответствии с изменяющимися условиями и методами обучения должны претерпевать изменения и модели, используемые для обучения. Из общего количества используемых в обучении моделей, число которых непрерывно возрастает в связи с накоплением новой научной информации, требующей новых форм демонстраций, необходимо выделять модели, интенсифицирующие процессы обучения, образующие взаимосвязанные комплексы средств обучения. Должна повышаться возможность иерархического распределения средств обучения и взаимного их сочетания в процессе обучения, соответствие определенным приёмам работы и формам деятельности. Также должна возрастать специализация моделей, то есть модели должны ярко и желательно однозначно отражать моделируемые качества. При этом должна сохраняться преемственность моделей, их совместимость и взаимозаменяемость.

Как было рассмотрено в первой главе диссертации, при использовании в процессе обучения моделей атома и элементарных частиц, его составляющих, существует проблема адаптации научных моделей для обучения. Научно-исследовательская модель электрона в виде волнового кольца из-за наличия внутренней структуры является сложной. С целью лучшей адаптации обучающих моделей на первом этапе использования можно не рассматривать сложную внутреннюю структуру электрона, а использовать в качестве упрощённой геометрической модели электрона простую форму замкнутого на себя потока энергии - кольцо (или тонкий тор). Такое предложение консервативно, но оправдано, тем более что получение прямых доказательств или опровержений предполагаемой структуры электрона до сих пор затруднено. Это связано с тем, что разрешение самого точного инструмента энтроскопии на сегодня - сканирующего электронного микроскопа колеблется от 2 до 20 Å [92] в то время как предполагаемый размер кольца – электрона порядка 1 Å. Поэтому целесообразным представляется не попытка создания модели, адекватной действительности, а постановка задачи создания работоспособной модели. Под работоспособностью подразумевается возможность использования модели во всех основных операциях, характерных для модельного эксперимента, сформулированных Штоффом В. А. [137, с.121]: построение модели, экспериментальное её исследование и переход от модели к натуральному объекту, состоящий в перенесении результатов, полученных в исследовании, на этот объект.

Анализ традиционных моделей, проведенный в первой главе диссертационного исследования, показал, что при современных тенденциях к разностороннему изучению строения атома, использование традиционных моделей не является достаточным для формирования целостной и взаимосвязанной картины строения атома, отличающейся простотой и наглядностью. Необходимо дополнить традиционно используемые в школе скелетные и шаро-стержневые модели [28, 73, 84,] кольцегранными моделями электронных оболочек атомов и молекул [4, 56]. Использование кольцегранных моделей позволяет демонстрировать электронное строение оболочек, причем не только внешних, но и внутренних. Эти модели характеризуются универсальным подходом к моделированию: каждый электрон оболочки любого атома изображается кольцом (или геометрической моделью в виде тонкого тора). Кольцегранные модели демонстрируют расположение электронов в атомах и соединениях, что позволяет изображать и объяснять формы атомов в объёмных моделях Стюарта, Полинга, орбитальных и молекулярных моделях Тартуского университета [55].

Поскольку кольцегранные модели конструктивно сложнее моделей Стюарта, предлагается для моделирования соединений с большим числом однотипных атомов использовать объемные модели Стюарта, предварительно рассмотрев электронное строение каждого, входящего в соединение, атома в виде кольцегранника.

Достоинства модели электрона в виде кольца заключаются не только в отсутствии недостатков старых моделей, но открывает новые возможности в моделировании. Изготавливаемые модели веществ подробнее описывают электронную структуру вещества, то есть являются более информативными. Использование этих моделей позволяет сжать объём информации, предназначенной для усвоения учащимися, за счет отсутствия сложных моделей молекулярных орбиталей. Большинство объяснений и демонстраций форм электронных орбиталей (или электронных облаков) и закономерностей их гибридизации можно опустить, используя одну простую модель электрона в виде кольца и простейший алгоритм моделирования электронных оболочек в виде кольцегранников. От использования метода моделирования электрона в виде кольца ожидается существенное повышение педагогической эффективности обучения. Появляется возможность строить наглядные модели электронных оболочек, что раньше было затруднено: в лучшем случае, изображались валентные электроны (мысленно вырванные из электронной оболочки) или “учитель предлагал учащимся мысленно располагать электронные облака каждого атома” [28, С.19], или изготавливались самодельные статические или динамические модели электронных облаков. В. В. Загорский, рассматривая то, как в системе вальдорфской педагогики преподаются различные предметы, сделал вывод, что «лучше исключить из программы 7 – 9 классов все абстракции (электронные орбитали, теорию гибридизации и даже современное обоснование периодического закона), оставив их для 10 – 11 классов» [43, с. 11]. Аналогичное предложение было сделано и без привлечения новых методов обучения при анализе методики изучения раздела «Общая химия». Т. В. Смирнова предлагала перенести изучение s- и p- орбиталей в углубленный курс или изучать их в разделе «Общая химия» [106]. Это тем более актуально, что существующая тенденция развития пропедевтических курсов химии [22, 42] и взаимосвязи курсов естествознания и химии приводят к тому, что «понятия о химическом элементе, простых и сложных веществах вводят в 6 и 7 классах, используя модели, в том числе изготавливаемые учениками из пластилина» [42, с. 30]. Егорова А.А. акцентирует внимание на том, что «школьники среднего возраста (11 – 13 лет) обладают гораздо большими способностями, чем те, на которые ориентируются традиционная педагогика и методика» [42, с. 31]. Следует более тщательно рассмотреть вопрос, с какого возраста возможно использование кольцегранных моделей, можно ли это делать в курсе естествознания с шестого класса, или только в курсе химии с 8 класса?

Рассматриваемые в старших классах современные представления об электронном и пространственном строении атомов и молекул убедительно свидетельствуют о том, что электронно-ядерные взаимодействия, приводящие к пониманию энергии системы, служат необходимым и достаточным условием возникновения химической связи. В связи с этим перекрывание облаков не причина (как об этом иногда говорят и пишут), а лишь следствие электронно-ядерных взаимодействий, приводящих к коллективизации ядер и образованию единого молекулярного электронного облака [134].

2.2. Педагогико-эргономические требования к моделям атомов и молекул

и их новые дидактические возможности.

К моделям, используемым в школе, предъявляется ряд требований:

1. Модели должны служить формированию у учащихся систематических и прочных научных знаний, а также практических умений и навыков.

2. Информация, передаваемая с помощью моделей, должна соответствовать современному состоянию науки и техники, опираться на фундаментальные знания.

3. Содержание, объем и глубина, заложенной в модели информации, должна соответствовать содержанию программы и познавательным возможностям учащихся, учитывать их подготовку и возрастные особенности.

4. Модель должна быть наглядной, обеспечивать быстроту и точность получения нужной информации.

5. К моделям обязателен объяснительный текст (описание, инструкция по сборке и хранению, схемы монтажа, методические рекомендации по их использованию на уроке и т.п.)

6. Модели должны быть простыми и удобными в работе (демонстрация, крепление, легкость сборки и разборки), в упаковке, хранении и транспортировке.

Поэтому при проектировании моделей необходимо учитывать общие педагогико-эргономические требования, обусловленные дидактическими возможностями и функциями этого вида средства обучения, а именно: информативность, адаптивность к определенному способу деятельности, инструментальность, комплементарность (свойство дополнять недостающие признаки и “работать” в системе с другими средствами обучения), а также специфические требования, продиктованные особенностями содержания учебного предмета и отбором наиболее предпочтительных наглядных форм [73]. Проектирование моделей опирается на систему педагогико-эргономических требований. Из них принцип научности обучения является важнейшим. Одновременно с принципом научности, принцип доступности требует, чтобы обучение строилось на уровне возможностей учеников, большое значение в использовании обучающих моделей играет возможность их адаптации к уровню знаний обучаемого. Сложность модели должна отражать не сложность моделей «переднего края науки», а уровень знаний субъекта обучения, должна соответствовать познавательным возможностям учащихся, их подготовке и возрастным особенностям. Спецификой учебных моделей является простота восприятия, напрямую связанная с неминуемой популяризацией и упрощением учебного материала. Важно, чтобы упрощение не происходило в ущерб научной достоверности, то есть адаптивность модели не должна входить в противоречие с её информативностью.

К общим педагогико-эргономическим требованиям относится инструментальность: максимальная простота и удобство использования моделей и однозначная их адресованность выбранным изучаемым явлениям или процессам, комплементарность: свойство дополнять недостающие признаки и “работать” в системе с другими средствами обучения. Комплементарность, или свойство дополнять недостающие признаки и “работать” в системе с другими средствами обучения, связана с требованием совместимости различных моделей: их взаимной непротиворечивости и возможности пересечения границ применения. В современных условиях развития средств обучения, основанных на компьютерных технологиях, важным качеством моделей является интерактивность, возможность представления динамических видео-образов и взаимодействия с ними с помощью компьютерных графических программ, компьютерной анимации и слайдов.

.

Схема 2. 2
Педагогико-эргономические требования

к проектированию моделей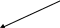














При проектировании моделей необходимо учитывать как общие педагогико-эргономические требования (схема 2.2), обусловленные дидактическими возможностями и функциями этого вида средств обучения, так и специфические требования, продиктованные особенностями содержания учебного предмета и отбором наиболее предпочтительных наглядных форм. Большое значение имеет возможность использования динамических моделей. Главным преимуществом динамических пособий по сравнению со статическими является то, что заложенная в них информация для восприятия представляется чаще всего не вся сразу, а определёнными порциями, постепенно. При использовании динамических средств наглядности достигается подлинное соответствие зрительного восприятия ходу, движению мышления.

Рассмотрена исторически сложившаяся последовательность употребления моделей атомов, молекул и составляющих их элементарных частиц, используемая в современной системе обучения. По мере продвижения научного познания и совершенствования науки развиваются, уточняются и обогащаются не только отдельные её понятия, но система понятий. Системный подход проявляется в системно-структурном и структурно-функциональном анализе понятий и их систем при изучении сложных химических объектов как целостных формирований. Одним из рациональных путей обучения химии и формирования систем понятий является структурирование понятийного содержания с целью его сжатия, упорядочения и выделения оптимальных вариантов раскрытия понятий курса. Вместе с понятийной базой развиваются информационные и технологические средства обучения, являющиеся существенной поддержкой курса, появляются новые модели. Наглядные модели, как существенная составная часть средств обучения, тоже должны быть объединены во взаимосвязанные комплексы.

Объективный процесс научного познания приводит к накоплению информации. В системе обучения этот процесс отражается увеличением количества используемых моделей, число которых непрерывно возрастает. Необходимо производить отбор моделей, удовлетворяющих требованиям необходимости и достаточности для организации полноценного процесса обучения. Возникает потребность иерархического распределения моделей и их соответствие определенным приемам работы и формам деятельности. Должна возрастать специализация моделей, то есть модели должны ярко и однозначно отражать моделируемые качества. При этом должна сохраняться преемственность моделей, их совместимость. Системность моделей, их способность работать в комплексе с другими средствами обучения также является современным педагогическим требованием.

Специфические требования к моделям определяются особенностями моделируемого объекта или моделируемой стороны оригинала и формой наглядного предъявления изучаемого материала. Как отмечено в [88, с.245], при создании и использовании наглядных пособий следует иметь в виду следующие два обстоятельства. Сначала происходит перенос знаний об изучаемом объекте на разрабатываемое наглядное пособие. Такой перенос знаний об изучаемом объекте на наглядные пособия, то есть конструирование их, проводится обычно учителем или методистами на основе дидактических требований, разработанных педагогикой и частными методиками. Когда наглядные пособия используются в школе, происходит второй (обратный) перенос знаний – переход от наглядных пособий к объектам изучения, например, от модели атома к его строению. Наибольшие затруднения при втором переносе встречаются в процессе изучения явлений микромира, например, строения атомов и молекул. Это связано с тем, что модель микрообъекта не отражает внешнего сходства с микрообъектом, а является только аналогией, отображением его структуры, своеобразной имитацией, и существует реальная опасность того, что учащиеся могут отождествить наглядное пособие с объектом изучения, например, динамическую модель атома могут воспринять как некую увеличенную копию атома. Следовательно, необходимо настойчиво подчеркивать, что эти модели лишь отражают структуру микрообъектов, принципы их строения, но не воспроизводят внешнего вида микрообъектов, они изоморфны по отношению к изучаемому микрообъекту.

При моделировании объектов микромира к специфическим требованиям можно отнести требование использования статических моделей с элементами динамики. В практике работы учителя используются и статические, и динамические наглядные пособия. Если в статических пособиях процессы отражены в целом, без их постепенного развития, то в динамических пособиях процессы показываются в развитии. Главным преимуществом динамических пособий по сравнению со статическими является то, что заложенная в них информация для восприятия представляется чаще всего не вся сразу, а определёнными порциями, постепенно. В этом случае внимание учащихся не рассеивается на разные объекты изучения, а концентрируется лишь на одном, определённом объекте или части его. Кроме того, при использовании динамической наглядности на первый план выступает непроизвольное внимание, которое постоянно поддерживается интересом к динамически развивающимся и обновляющимся деталям пособия.

При использовании динамических средств наглядности достигается подлинное соответствие зрительного восприятия ходу, движению мышления. Например, если сравнить различные статические пособия по строению атомов и химической связи (схемы, таблицы, шаро-стержневые модели и пр.) с динамическими, то оказывается, что учащиеся воспринимают последние с большим интересом. В этом случае в средней школе можно успешно вводить элементарные квантово-механические представления о строении атомов и молекул.

Наряду с положительными качествами динамических пособий необходимо отметить и некоторые их недостатки. Главный из них – невозможность длительной демонстрации изображаемого явления. Статические пособия дают возможность длительной демонстрации изучаемого объекта перед учащимися. В этом случае исходные и промежуточные образы демонстрируемого пособия не исчезают, что облегчает процесс восстановления пройденного пути рассуждения. Учитывая положительные и отрицательные качества этих различных средств наглядности, нельзя резко противопоставлять их друг другу, отрицать одни из них и заменять другими. Наиболее целесообразным является их оптимальное сочетание в определённых педагогических ситуациях [88, с.248]. Более технологичным и современным подходом к использованию средств наглядности представляется использование моделей статических по характеру, но имеющих частично динамические функции, а именно, разборные, позволяющие отображать на них процессы, имеющие место в моделируемых объектах. Например, такие химические процессы как образование молекул из атомов, образование ионов, потерю или присоединение электрона атомом или молекулой.

Ещё одной особенностью наглядных моделей объектов микромира является их повышенная тенденция к приобретению новых свойств, качеств или особенностей. Это связано с тем, что точного представления объектов микромира – атомов и молекул пока нет, а способы их отображения продолжают меняться и совершенствоваться. В более общем виде это сформулировано Б. Т. Лихачевым: «Главное противоречие формирования содержания общеобразовательной школы состоит в том, что количество новой научной, технической, культурной информации, в свете которой расширяется, уточняется, пересматривается содержание общего среднего образования, постоянно нарастает, а время на её усвоение, если и не уменьшается, то остается неизменным. Поэтому педагогика исходит из необходимости создания стабильной системы основ наук, её постоянного совершенствования, замены устаревших обобщений новыми, более полными, более ёмкими» [60, с. 327]. Поэтому к используемым моделям атомов и молекул следует предъявлять дополнительные специфические требования. Модели должны иметь возможность взаимосовместимости, то есть предоставлять возможности для создания развивающихся, сменяющих друг друга образов, сопровождающих процесс познания от простого к сложному. Это качество можно сформулировать как перспективность, возможность развития и гибкой адаптации к новым моделям. Перспективность, как дидактическая функция, заключает в себе возможность развития и совершенствования наглядных моделей и использования их для возвращения к рассмотрению ранее изученного материала на новом, более сложном уровне, иллюстрирующимся более сложными, развёрнутыми моделями.

Рассмотрим, как удовлетворяет общим и специфическим педагогико-эргономическим требованиям предложенная модель электрона в виде тонкого тора, или кольца и обладают ли новыми дидактическими возможностями получаемые с её помощью кольцегранные модели атомов и молекул.

Модель электрона в виде тонкого тора, или кольца, позволяет изображать электронные оболочки атомов в виде кольцегранников. Их построение наглядно демонстрирует принцип Паули, так как каждый электрон занимает индивидуальное место в оболочке. Их геометрически различное расположение это демонстрирует, объясняя магнитное расщепление спектральных линий различной ориентацией образующихся в момент излучения диполей “ядро - электрон”. Также отпадает необходимость постулировать правила Бора. Наглядность кольцевой модели электрона, локализованного в атоме, позволяет представлять постулаты в виде очевидных свойств, проявляемых электроном в атоме. Эти свойства не требуют постулирования - достаточно описания и демонстрации. Частицы, находящиеся в стационарном состоянии, изображаются покоящимися кольцами, и представляют собой волновые процессы, локализованные, или заключенные, в пределах эквипотенциальной поверхности. А любые перемещения заряда в пределах эквипотенциальной поверхности, то есть без изменения потенциала, не приводят к совершению работы и не должны сопровождаться излучением. Излучение происходит только при переходе из одного стационарного состояния в другое, характеризующееся другим потенциалами и другим, соответствующим ему, энергетическим уровнем.

При использовании материальной модели электрона в виде кольца, модель электронных оболочек выглядит кольцегранником, состоящим из числа колец, равного числу электронов (рис. 1, 2, 3, 4, 5). Двухцветные модели завершенных атомных оболочек своей симметрией и чередованием цветов (обозначающих направление вектора магнитного момента к ядру или от ядра) демонстрируют свою устойчивость. Электронные конфигурации атомов, имеющих две и более электронных оболочек, моделируются в виде нескольких кольцегранных фигур, вложенных одна в другую и имеющих общий центр, совпадающий с ядром атома (рис. 12).

Наборы для создания кольцегранных моделей атомов и молекул, как демонстрационные, так и раздаточные, должны позволять моделировать геометрическую форму электронных оболочек, подразумевая наличие электрических и магнитных свойств у электронов, изображаемых цветными кольцами. Окраска моделей, когда она не регламентирована стандартами и принятыми правилами, должна способствовать выделению информативных элементов. Цветовое решение должно соответствовать психофизиологическим особенностям восприятия. Кроме того, окраска отдельных частей модели должна быть аналогична цветам в других средствах, используемых при изучении учебного материала. Наиболее предпочтительны для цветового кодирования следующие цвета: фиолетовый, голубой, зеленый, желтый, красный. Модели должны быть изготовлены из материалов, сохраняющих форму и окраску в течение срока эксплуатации не менее 8 лет. Предпочтительны синтетические полимеры, не выделяющие токсических веществ [91]. Набор изготавливается из стойких пластмасс основных рекомендованных цветов.

В условиях развития системы средств обучения, включающей компьютерные технологии, используемые модели должны иметь возможность быть представленными в виде компьютерных программ и динамических видеообразов (компьютерных фильмов или слайдов). Бурное развитие компьютерной графики и легкость получения на экране информации в виде псевдо-трёхмерных образов приводит к избалованности сознания и избирательности внимания. В таких условиях для удержания внимания на предмете обучения необходимо создание ярких, взаимосвязанных, быстро развивающихся образов. Образная модель является посредником между чувственно воспринимаемыми объектами действительности и смыслом, значением, понятой сущностью их [142]. Образное мышление позволяет увеличить объем усваиваемой информации за счет использования развивающихся, сменяющих друг друга образов, сопровождающих процесс познания от простого к сложному.

Компьютерное моделирование позволяет добиться высокой скорости смены информационно насыщенных образов, стимулирующих умственную деятельность. Но компьютерные модели пока не могут полностью заменить материальные модели. Осязательные ощущения и возможность проведения самостоятельных и практических работ по сборке и манипуляции материальными моделями остается наиболее действенным способом обучения, который не может быть заменён на компьютерное моделирование. Сильной стороной использования компьютерных моделей является лёгкость и возможность быстрого повторения изученных материалов. Это делается представлением ранее изученных материалов – образов моделей, обобщая и дополняя комплекс обучающих моделей, чем и способствует поставленной цели: формированию целостного знания о строении вещества.

Простота демонстрации устойчивости электронных оболочек в виде кольцегранников позволила реализовать экспериментальную компьютерную программу для обучения строению атома и изучения Периодического закона и Периодической системы химических элементов Д.И. Менделеева. Эта обучающая компьютерно-графическая программа “Глобус атома” содержит элементы игры и предназначена для использования в 8-10 классах средней образовательной школы. Она сделана под оболочкой «Windows» и адаптирована к различным по быстродействию персональным компьютерам, в зависимости от комплектации школьных компьютерных классов.

Обучающая компьютерно-графическая программа “Глобус атома” состоит из двух частей.