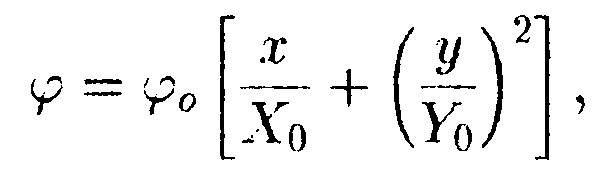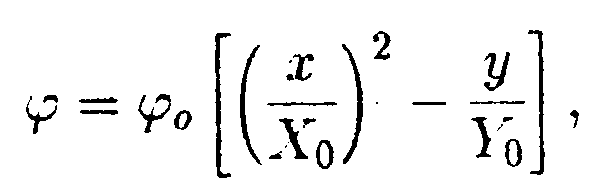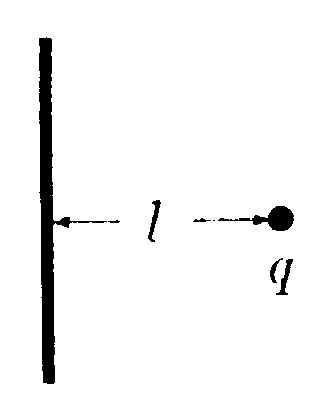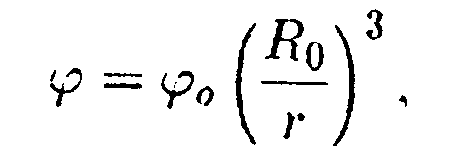Часть II Электричество и магнетизм. Сборник задач по общей физике Часть II. Электричество и электромагнетизм Под ред. Э. Б. Селивановой Библиотека Ново иб и, с ко го

• Название: Сборник задач по общей физике Часть II. Электричество и электромагнетизм Под ред. Э. Б. Селивановой Библиотека Ново иб и, с ко го
• Анкор: Часть II Электричество и магнетизм.doc
• Дата: 24.12.2017
• Размер: 40.78 Mb.
• Имя файла: Часть II Электричество и магнетизм.doc
• Тип: Сборник задач; #12775
• страница: 4 из 9

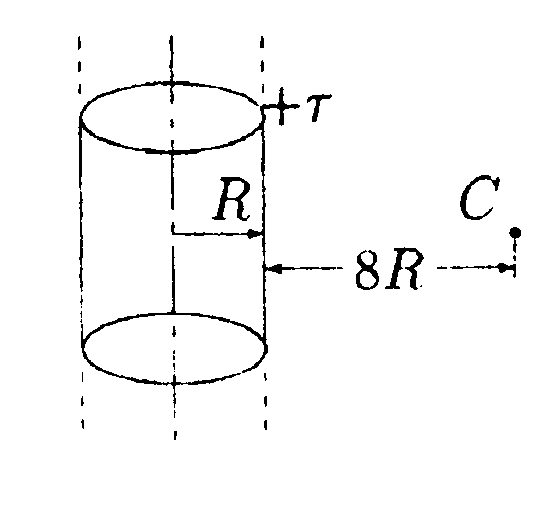
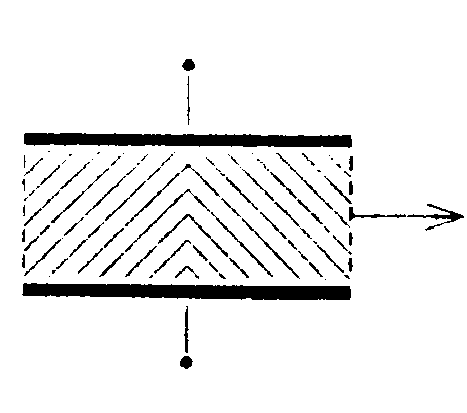
6.2. Вариант 2

• 6.2.1. Определите работу электрических сил по
переносу пробного заряда q= 1,0 • 10ˉ⁹Кл из
точки С в точку В, если а = 10 см, b =
20 см, q1 = 3,3 • 10ˉ⁹Кл и q₂= 6,6 • 10ˉ⁹Кл.

• 6.2.2. Какая работа А совершается при перенесении точечного заряда
q = 20 нКл из бесконечности в точку, находящуюся на расстоянии
∆r = 1,0 см от поверхности шара радиусом R= 1,0 см с поверхностной
плотностью заряда σ = 10 мкКл/м².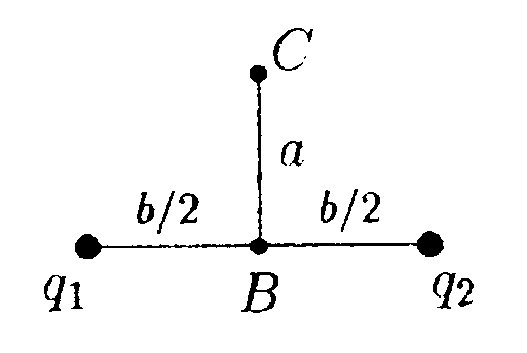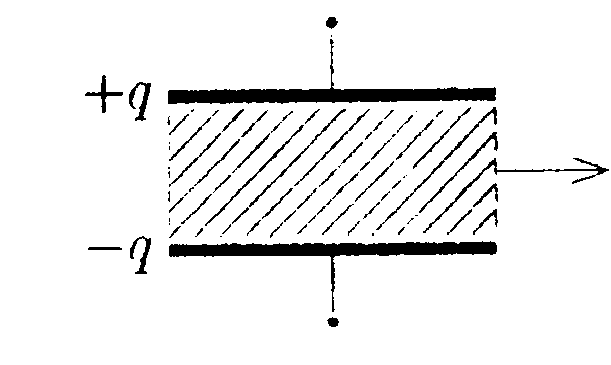

•



6.2.3. Найдите работу, которую нужно затратить, чтобы вынуть диэлектрик из плоского кон­денсатора, если заряд на пластинах поддержива­ется постоянным и равным q = 6,0 мкКл. Пло­щадь пластин S = 100 см², расстояние между пластинами d=0,3 см. а диэлектрическая про­ницаемость диэлектрика ε = 2,0.

• 
  6
  
  .2.4. С поверхности бесконечного равномерно за­
  ряженного прямого цилиндра с линейной плотностью заряда r=50 нКл/м вылетает α-частица с нулевой начальной скоростью. Опреде­лите кинетическую энергию a-частицы в точке
  С, находящейся на расстоянии 8Rот поверх­ности цилиндра, где R- радиус цилиндра,
  (q_a= 3,2 • 10^-19Кл, ma= 6,67 • 10^-27кг.)
  
• 
  6.2.5. Потенциал электрического поля имеет вид:
  

г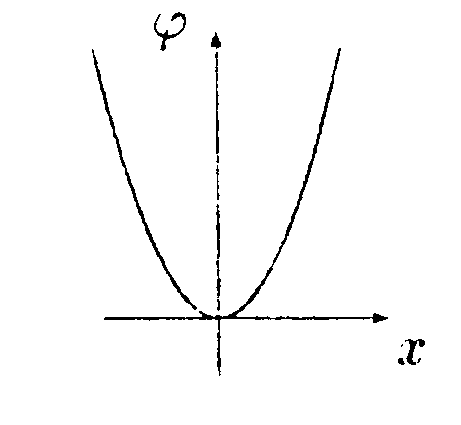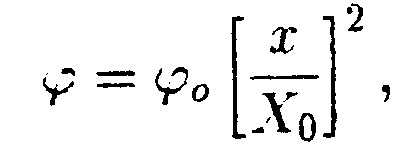



де φ_о = 1000 В, Хо = 2,0 м. Найдите зависимость напряженности электрического поля Е от х и изобразите ее на графике.

• 6.2.6. Металлический шар радиусом R1= 3,0 см, имеет заряд q1 =
= -20 нКл, окружен концентрически расположенной сферой радиусом R2 = 5,0 см, равномерно заряженной по поверхности зарядом q2 =40 нКл. Найдите напряженность электрического поля Е и потенциал φна расстояниях r1 = 2,0 см, r2 = 4,0 см и rз = 6,0 см.

• 6.2.7. Как нужно соединить конденсаторы с емкостями С1 = 2,0 пФ, C2= 4,0 пФ и Сз = 6,0 пФ, чтобы получить систему с емкостью С = 3,0 пФ?

6.3 . Вариант 3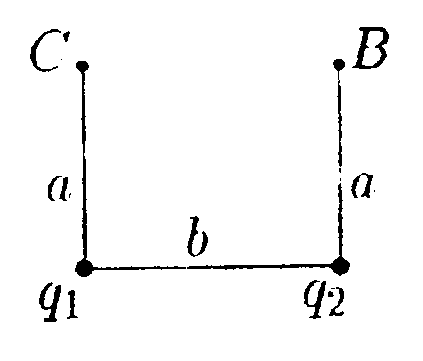

•

6.3.1. Определите работу электрических сил по переносу пробного заряда q=2,0 нКл из точки С в точку В, если а= 4,0 см, b= 3,0 см, q1 = 3,0 нКл, q₂ = 6,0 нКл.

• 6.3.2. На расстоянии r1 = 4,0 см от бесконечно длинной заряженной нити находится точечный заряд q = 0,66 нКл. Под действием поля заряд приближается к нити до расстояния r2 = 2,0 см. При этом совершается работа А = 50 • 10ˉ⁷Дж. Найдите линейную плотность заряда rна нити.
• 6.3.3. Найдите работу А, которую нужно затратить, чтобы увеличить расстояние х между пластинами плоского воздушного конденсатора, заряженного разноименными зарядами Q = 0,2 мкКл, на величину ∆x= 0,2 мм. Площадь каждой из пластин конденсатора S= 400 см².

• 6.3.4. При радиоактивном распаде из ядра атома полония вылетает α-
частица со скоростью V= 1,6·10ˉ⁷ м/с. Найдите разность потенциалов электрического поля U, в котором можно разогнать покоящуюся
α-частицу до такой скорости. (qa = 3,2 • 10-¹⁹Кл, ma= 6,67 • 10ˉ²⁷кг.)

• 6.3.5. Зависимость потенциала электрического
поля φот координаты х имеет вид, показанный
на рисунке. Найдите зависимость напряженности электрического поля Е от х и изобразите ее
на графике.

• 
  6.3.6. Электростатическое поле создано длинным цилиндром радиусом R = 1,0 см, равномерно заряженным с линейной плотностью
  r = 20 нКл/м Определите разность потенциалов двух точек этого поля,
  находящихся на расстоянии а1= 0,5 см и а2= 2,0 см от поверхности
  цилиндра, в средней его части.
  
• 
  6.3.7. Заряженный шар 1 радиусом R1 = 2,0 см приводится в сопри-
  косновение с незаряженным шаром 2, радиус которого R2= 3,0 см.
  После того как шары разъединили, заряд шара 2 оказался равным
  q₂ = 3,0 мкКл. Какой заряд q1был на шаре 1 до соприкосновения с
  шаром 2 ?
  

6.4, Вариант 4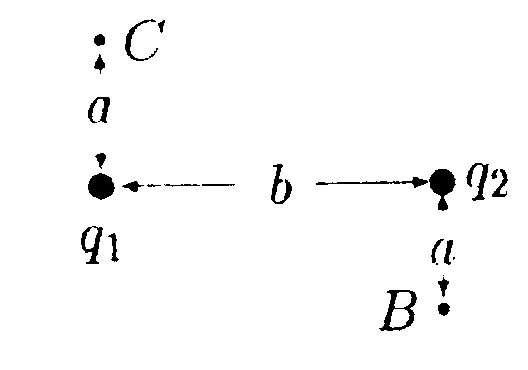

•

6.4.1. Определите работу электрических сил по
переносу пробного заряда q= 1,0 • 10ˉ⁹Кл из
точки С в точку В, если а = 6,0 см, b=8,0 см,
q1 = 6,0 • 10ˉ⁹Кл и q2= -12 • 10ˉ⁹Кл.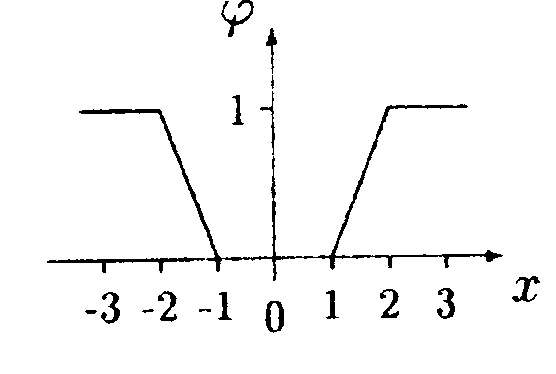

•

6.4.2. На расстоянии r1= 10 см от центра равномерно заряженной по
поверхности сферы радиусом R= 1.0 см находится точечный заряд
q = 1,0 нКл. Под действием электрического поля сферы заряд qперемещается в точку, находящуюся на расстоянии r2= 15 см от центра
сферы. При этом совершается работа A = 3,0 • 10ˉ⁷Дж. Найдите потенциал сферы φ.
• 6.4.3. Какую работу надо совершить, чтобы увеличить расстояние
между пластинами плоского вакуумного конденсатора с площадью пластин S=100 см² от расстояния х1 = 0,03 м до расстояния x2 = 0,10 м?
Напряжение между пластинами конденсатора постоянно и равно U =220 В.

• 
  6.4.4. На тонком кольце радиусом R= 0,10 м равномерно распределен заряд q= 2,0 мкКл. Какую наименьшую скорость Vнеобходимо
  сообщить находящемуся в центре кольца маленькому шарику массой
  т = 1,0 мг с зарядом q0= -3,0 нКл. чтобы он мог удалиться от
  кольца в бесконечность?
  
• 
  6.4.5. Потенциал поля, создаваемого некоторой системой зарядов, имеет
  вид φ = E0(x+ у), где E0= 1,0 • 10⁴ В/м. Изобразите примерный вид
  силовых и эквипотенциальных линий и найдите напряженность электрического поля Е как функцию координат.
  
• 
  6.4.6. Расстояние между пластинами плоского конденсатора d= 1,0 см.
  К пластинам приложена разность потенциалов U = 300 В. В пространстве между пластинами находятся плоско-параллельная пластинка парафина (εП = 3,0) толщиной d1 = 0,50 см и плоско-параллельная пластинка стекла (ε_с= 9,0) толщиной d2 = 0,50 см. Найдите напряженности Е1и E2электрического поля и падение потенциалов U1 и U2в каждом слое.
  

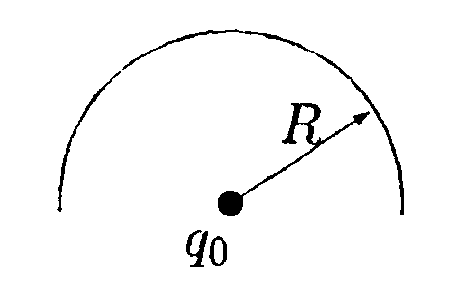
• 6.4.7. Каким будет потенциал металлического шара радиусом r=3,0 см, если сообщить ему заряд q = 1,0 нКл и окружить металлической сферой радиусом R = 4,0 см, соединенной с землей ?

6.5 . Вариант 5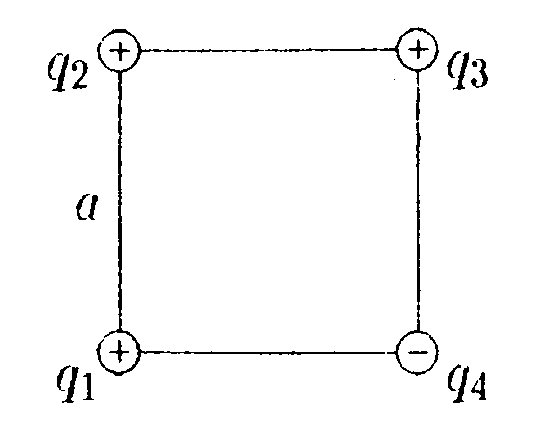

•

6.5.1. В вершинах квадрата со стороной а = 5,0 см находятся заряды: q1= +10 • 10ˉ⁹Кл. q₂= +2,0 • 10ˉ⁹Кл, q3= +3,0·10ˉ⁹Кл и q₄= = - 4,0·10ˉ⁹Кл. Какую работу нужно совершить, чтобы медленно удалить заряд q4на бесконечность?

• 6.5.2. Шарик, заряженный до потенциала φ = 792 В, имеет поверхностную плотность заряда σ= 333 нКл/м². Найдите радиус шарика R.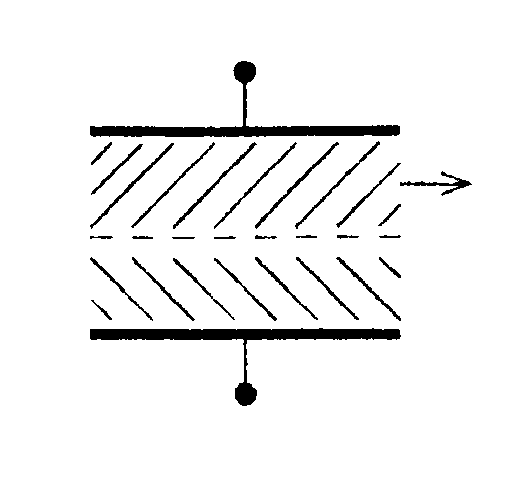
•

6.5.3. Найдите работу, которую нужно затратить, чтобы вынуть одну половинку диэлектрика из плоского конденсатора, если напряжение между пластинами поддерживается постоянным и равным U= 300 В. Площадь пластин S= 250 см², расстояние между пластинами d= 1,0 см, а диэлектрическая проницаемость диэлектрика ε = 3,0.

• 
  6.5.4. Электрическое поле образовано положительно заряженной бесконечно длинной нитью с линейной плотностью заряда r = 0,2 мкКл/м.
  Какую скорость Vполучит электрон под действием поля, приблизив-
  шись к нити с расстояния r1= 1,0 см до расстояния r2 = 0,5 см?
  
• 
  6
  
  .5.5. Потенциал поля, создаваемого некоторой системой зарядов, имеет
  вид
  

где φ₀ =1000 B, Х_о = 1,0 м, Y_о = 4,0 м. Изобразите примерный вид силовых и эквипотенциальных линий и найдите напряженность поля Е в точке С с координатами х_с = 5,0м и у_с = 2,0м.

• 6.5.6. Электрическое поле создано тонким стержнем равномерно заря­женным с линейной плотностью зарядаr = 2,1 мкКл/м. Определите
потенциал поля в точке, удаленной от концов стержня на расстояние,
равное длине стержня.

• 6.5.7. Конденсатор емкостью С1, заряженный до напряжения U1=
=100 В, соединяется с конденсатором емкостью С2 = 2С1. заряженным до напряжения U2 = 200 В. параллельно (положительная обкладка с положительной, отрицательная с отрицательной). Какое напряжение установится между обкладками?

6.6 . Вариант 6

• 6.6.1. Два точечных заряда q1 = 6,66 нКл и q2 = 13,33 нКл находятся на расстоянии r1= 40 см. Какую работу А надо совершить, чтобы сблизить их до расстояния r2= 25 см?
• 6.6.2. Поверхностная плотность заряда металлической сферы σ= 0,33 мкКл/м². Потенциал сферы на расстоянии ∆r = 1,5 см от поверхности равен φ = 750 В. Найдите радиус Rсферы.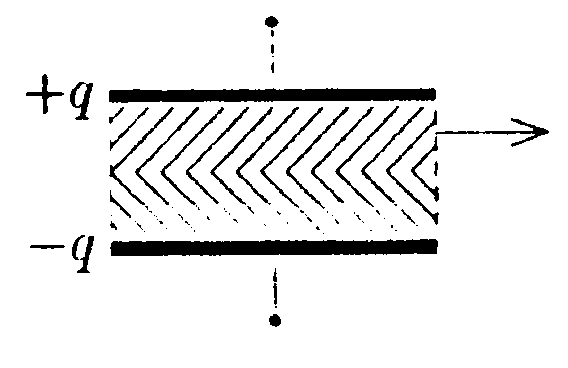

•

6.6.3. Найдите работу, которую нужно затратить, чтобы вынуть одну половинку диэлектрика из плоского конденсатора, если заряд на пластинах поддерживается постоянным и равным q = 5,0 мкКл. Площадь пластин S=50 см², расстояние между пластинами d = 0,3см, а диэлектрическая проницаемость диэлектрика ε = 2,0.

• 
  6.6.4. Шарик массой m = 0,2 г и зарядом q = +10 нКл перемещается
  из точки 1, потенциал которой φ1 = 5,0 • 10³ В, в точку 2, потенциал
  которой φ2= 0. Найдите скорость шарика в точке 1, если в точке 2 она
  стала равной V2 = 1 м/с.
  
• 
  6
  
  .6.5. Потенциал поля, создаваемого некоторой системой зарядов, имеет
  вид
  

где φ₀ = 1000 В, X0=2,0 м, Y0= 1,0 м. Изобразите примерный вид силовых и эквипотенциальных линий и найдите напряженность поля Е в точке С с координатами х_с = 1,0 м, и у_с= 2,0 м.

• 
  6
  
  .6.6. Имеется непроводящая оболочка сферической формы с одинаковой объемной плотностью
  заряда р. Найдите напряженность и потенциал
  поля на расстоянии rот центра. Изобразите на
  графике зависимости Е и φот r.
  
• 
  6
  
  .6.7. Точечный заряд q = 100 мкКл находится
  на расстоянии l = 1,5 см от проводящей плоскости. Найдите энергию взаимодействия этого
  заряда с зарядами, индуцированными на плоскости.
  

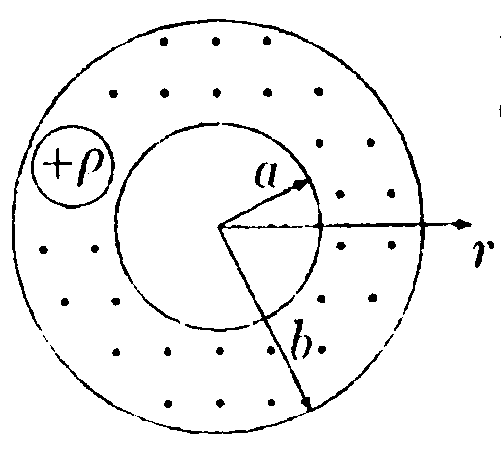
6.7. Вариант 7

• 6.7.1. В вершинах равностороннего треугольника со стороной а = 7,0 см находятся заряды: q1 = 1,0 · 10ˉ⁹Кл, q₂= 3,0 • 10ˉ⁹Кл, q3 =6,0 • 10ˉ⁹Кл, а в центре - пробный заряд q =0,3 • 10ˉ⁹Кл. Какую работу нужно совершить,
чтобы медленно удалить заряд qна бесконечность?

• 6.7.2. Найдите потенциал φточки поля, находящейся на расстоянии r = 10 см от центра заряженного по поверхности шара радиусом
R= 1,0 см, если потенциал шара φо = 300 В.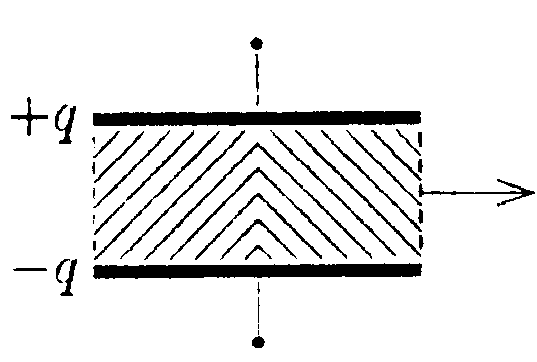

•

6.7.3. Найдите работу, которую нужно затратить, чтобы вынуть одну половинку диэлектрика из плоского конденсатора, если заряд на пластинах поддерживается постоянным и равным q = 10 мкКл. Площадь пластин S = 100 см², расстояние между пластинами d = 0,5см, а диэлектрическая проницаемость диэлектрика ε = 2,0.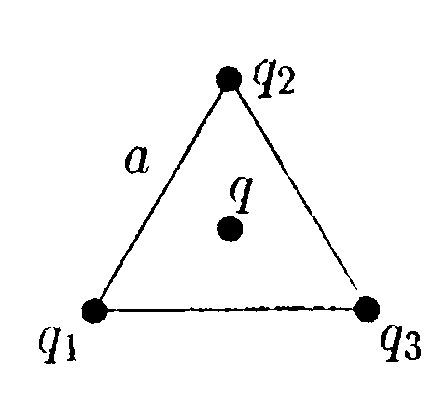

•

6.7.4. Электрическое поле образовано положительно заряженной бесконечной длинной нитью. Двигаясь под действием этого поля от точки,
находящейся на расстоянии r1 = 1,0 см от нити, до точки, находящейся
на расстоянии r2 = 4,0 см от нити, α-частица изменила свою скорость
от V1 =2 • 10⁵ м/с до V2 = 3 • 10⁶ м/с. Найдите линейную плотность
заряда r на нити. (q_a= 3,2 • 10ˉ¹⁹Кл. т_σ = 6,67 • 10ˉ²⁷кг.)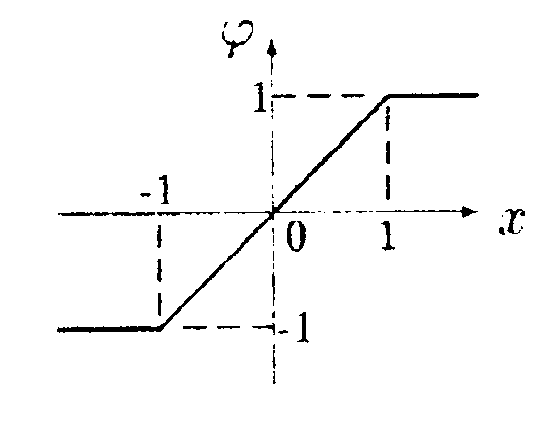

•

6.7.5. Зависимость потенциала электрического
поля φ от координаты х имеет вид. показанный
на рисунке. Найдите зависимость напряженности электрического поля Е от х и изобразите ее
на графике.

• 6.7.6. Заряд Qравномерно распределен по объему шара радиусом Rиз непроводящего материала. Найдите напряженность поля и
потенциал на расстоянии rот центра шара. Постройте графики зависимости Е и φ от r. Диэлектрическая проницаемость шара ε = 3,0.
• 6.7.7. Конденсатор емкостью С1 = 10 мкФ заряжен до напряжения
U =10 В. Определите заряд на обкладках этого конденсатора после
того, как параллельно ему был подключен другой, не заряженный, конденсатор емкостью С2 = 20 мкФ.

6.8 . Вариант 8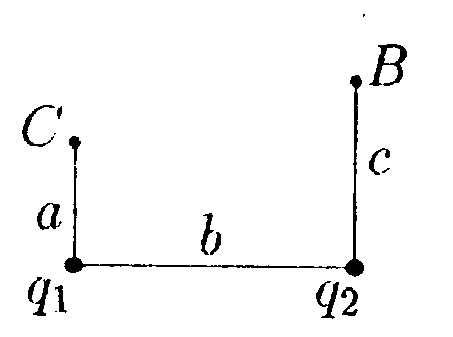

•

6.8.1. Определите работу электрических сил по
переносу пробного заряда q = 1,0 • 10ˉ⁹Кл из
точки С в точку В, если а = 3.0 см, b = 4,0 см, с = 6,0 см, q1= 3,0 • 10ˉ⁹ Кл и q₂ = -6,0•10ˉ⁹Кл.

• 
  6
  
  .8.2. На тонком полукольце радиусом R = 5 см
  равномерно распределен заряд q = 5мкКл.
  В центре полукольца находится пробный заряд
  q₀= -0,1 мкКл. Какую работу надо совершить,
  чтобы удалить пробный заряд q0 на бесконечность?
  
• 
  6
  
  .8.3. Найдите работу, которую нужно затратить, чтобы вынуть одну половинку диэлектрика из плоского конденсатора, если напряжение между пластинами поддерживается постоянным и равным U =200 В. Площадь каждой
  пластины S = 100 см², расстояние между пластинами d = 0,5 см. а диэлектрическая проницаемость диэлектрика е= 2,0.
  

• 
  6.8.4. Электрон летит от одной пластины плоского конденсатора до другой. Разность потенциалов между пластинами U = 3,0 кВ. а расстояние между ними d = 5,0 мм. Найдите скорость V, с которой электрон
  приходит ко второй пластине, и поверхностную плотность зарядов на
  пластинах σ. (q_e = 1,6 • 10ˉ¹⁹Кл, т_е= 9,1 • 10ˉ³¹кг).
  
• 
  6
  
  .8.5. Зависимость потенциала электрического поля имеет вид
  

где φ_о = 1000 В, R0 =1,0 м. Найдите зависимость напряженности электрического поля Е от rи вычислите значение Е при r= 3,0 м.

• 
  6.8.6. Металлический шар радиусом R1, заряженный до потенциала φ,
  окружают концентрической сферической проводящей оболочкой радиу­сом R2 , Чему станет равен потенциал шара, если заземлить внешнюю оболочку?
  
• 
  6.8.7. Конденсатор емкостью С1=1,0 мкФ выдерживает напряже­ние U1 = 6,0 кВ, а конденсатор емкостью С2= 2,0 мкФ - не более U₂= 4,0 кВ. Какое напряжение может выдержать система из этих двух конденсаторов при последовательном соединении?
  

6.9 . Вариант 9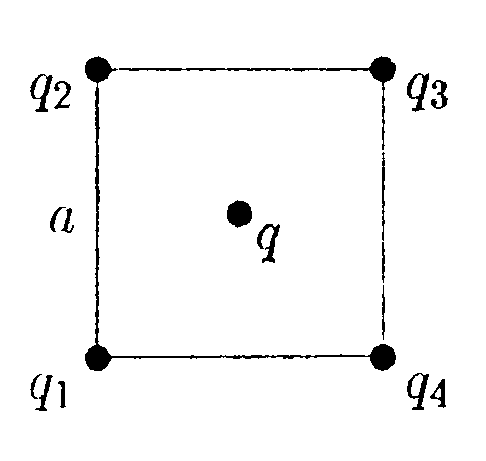

• 6.9.1. В вершинах квадрата со стороной а = =5,0 см находятся заряды: q1 = 1,0 • 10ˉ⁹Кл, q2 =2,0•10ˉ⁹Кл, q₃=3,0•10ˉ⁹Кл, q4=4,0•10ˉ⁹Кл, а в центре - пробный заряд q = 1,0•10 ˉ¹⁰Кл. Ка­кую работу нужно совершить, чтобы медленно удалить заряд qна бесконечность?

• 
  6.9.2. Параллельно бесконечно протяженной заряженной плоскости с
  поверхностной плотностью заряда σ = 20 нКл/м² расположена бес­конечно длинная заряженная нить с линейной плотностью заряда
  r = 0,4 нКл/ м. Определите работу по перемещению нити (в расчете на
  единицу длины нити) вдоль силовых линий электрического поля плоскости на расстояние ∆х = 3,0 см.
  
• 
  6.9.3. Площадь пластин плоского воздушного конденсатора S = 0,01 м².
  а расстояние между ними d= 5,0 мм. Какая разность потенциалов U
  была приложена к пластинам, если известно, что при разряде конден­сатора выделилось Q = 4,19 МДж тепла?
  
• 
  6.9.4. Два электрона в состоянии покоя помещены на расстоянии а =1,0 см друг от друга. Затем, под действием сил взаимного отталки­вания, они начинают двигаться. Определите предельную скорость V каждого электрона.
  
• 
  6.9.5. Потенциал поля, создаваемого некоторой системой зарядов, имеет
  вид φ= А(х²+ y²), где А = 100 В/м². Изобразите примерный вид силовых и эквипотенциальных линий и найдите напряженность поля Е в точке С с координатами х_с = у_с = 2,0 м.
  

• 
  6.9.6. Металлический шар радиусом R1= 10 см заряжен до потенциала
  φ1= 300 В. Каким станет потенциал этого шара φ после того, как его
  окружат сферической проводящей оболочкой радиусом R2= 15 см и
  соединят с ней проводником?
  
• 
  6.9.7. Пространство между пластинами плоского конденсатора запол­нено двумя слоями диэлектрика: слой стекла толщиной d1 = 0,2 см и
  слой парафина толщинойd2= 0,3 см. Разность потенциалов между об­
  кладками U= 300 В. Найдите плотность энергии электрического поля
  в каждом слое. ( ε_СТ = 9,0, ε_п =3,0).