Часть II Электричество и магнетизм. Сборник задач по общей физике Часть II. Электричество и электромагнетизм Под ред. Э. Б. Селивановой Библиотека Ново иб и, с ко го

• Название: Сборник задач по общей физике Часть II. Электричество и электромагнетизм Под ред. Э. Б. Селивановой Библиотека Ново иб и, с ко го
• Анкор: Часть II Электричество и магнетизм.doc
• Дата: 24.12.2017
• Размер: 40.78 Mb.
• Имя файла: Часть II Электричество и магнетизм.doc
• Тип: Сборник задач; #12775
• страница: 2 из 9

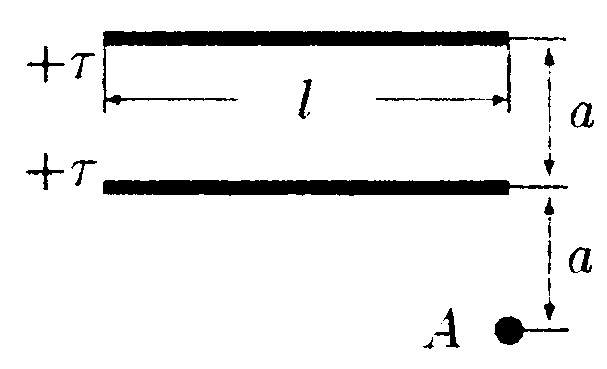
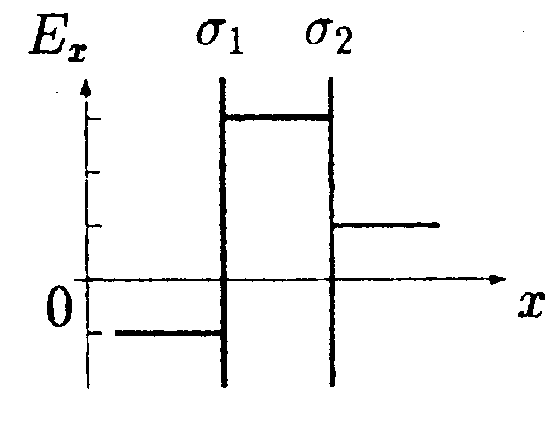
5.6. Вариант 6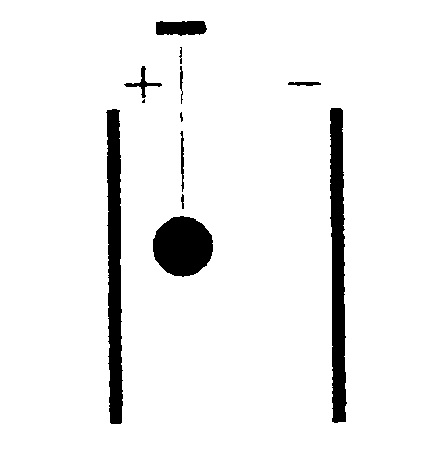

•


5.6.1. Между вертикально расположенными пла­стинами плоского конденсатора висит на длин­ной шелковой нити диэлектрический незаряжен­ный шарик, причем к одной пластине он распо­ложен ближе, чем к другой. Как должен вести себя этот шарик?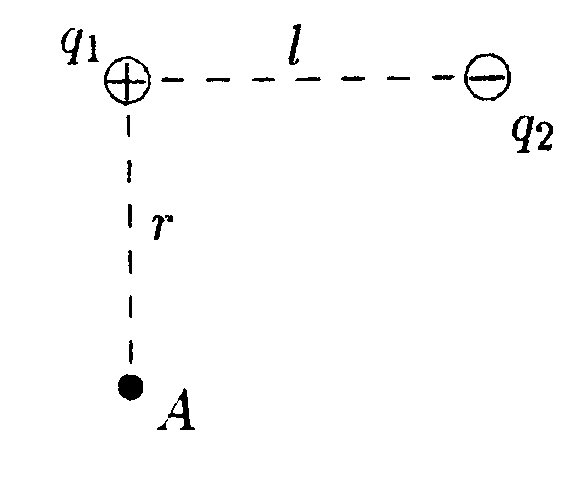

•

5.6.2. Заряды q1= 10 мкКл и q2 = —10 мкКл находятся на расстоянии l = 10 см. Определите на­пряженность электростатического поля в точке А, лежащей на перпендикуляре к линии, соеди­няющей заряды, и удаленной от q1на расстояние г = 10 см.

5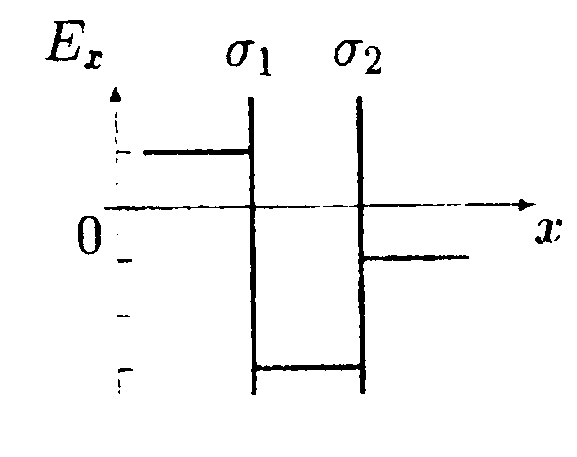

.6.3. Плоский конденсатор состоит из двух пластин, разделенных сте­клом с диэлектрической проницаемостью ε = 6,0. Какое давление ис­пытывает стекло перед пробоем, если напряженность электрического поля перед пробоем Е = 30•10⁶B/м?



• 5.6.4. На рисунке показано распределение на­пряженности электростатического поля Е_х(х), созданного двумя параллельными заряженными х бесконечными пластинами, вдоль направления х. Как различаются поверхностные плотности за­рядов σ1 и σ2 на этих пластинах по знаку и по модулю?

• 5.6.5. Плоская квадратная рамка со стороной а = 10 см находится на не­котором расстоянии от бесконечной равномерно заряженной плоскости с поверхностной плотностью заряда σ = +1,0 мкКл/м². Поверхность рамки составляет угол β = 30° с линиями напряженности поля, создан­ного плоскостью. Найдите поток вектора электрического смещения ФD через плоскость рамки.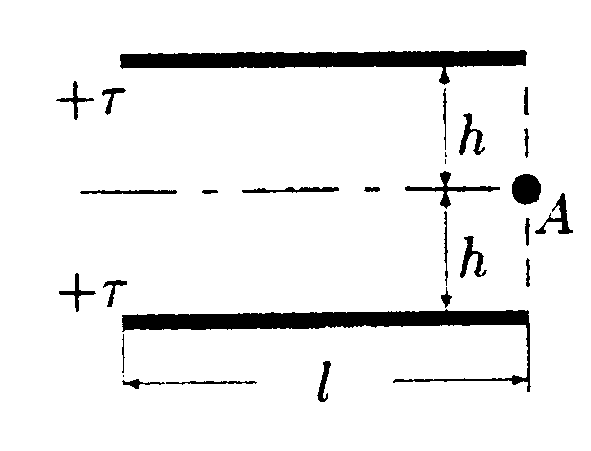


•

5.6.6. Используя принцип суперпозиции, найдите напряженность электростатического поля Е, которое создают в точке А параллельные равно- мерно заряженные с линейной плотностью заряда r = 1,0•10ˉ⁸Кл/м тонкие нити длиной l= -0,50 м. Точка А находится в одной плоскости с нитями и удалена от каждой нити на расстояние h= 0,20 м.

•

5.6.7. Металлический шар радиусом Rпомещен в сферическую концентрическую полость ради­усом 2Rдругого металлического шара, радиус которого равен 3R. Заряд большого шара +8q, малого шара +q. Постройте график зависимости напряженности электростатического поля Е от r, где r - расстояние от центра шаров. Для на­хождения зависимости Е(r) используйте теорему Гаусса.

5.7 Вариант 7

• 5.7.1. Как будет вести себя диполь в каждом из электростатических полей, изображенных на рисунках а, б, в?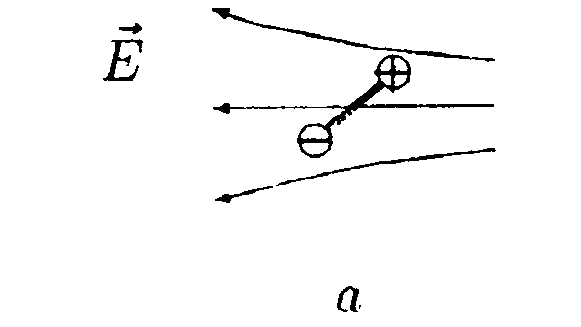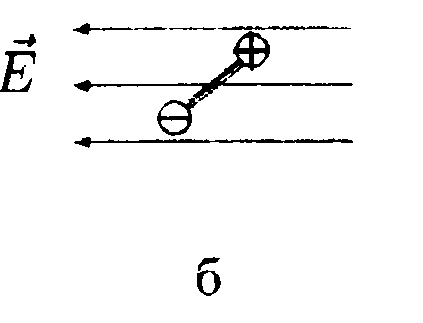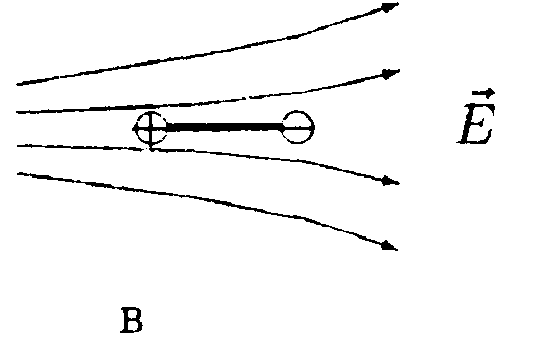

• 
  5.7.2. Определите напряженность электростатического поля в центре
  шестиугольника со стороной а, в вершинах которого расположены:
  а) равные заряды одного знака; б) заряды равные по модулю, но че­редующиеся по знаку.
  
• 
  5.7.3. Пластины плоского конденсатора площадью 1.0-10ˉ²м² каждая
  притягиваются с силой 1,2 . 10ˉ²Н. Пространство между пластинами
  заполнено диэлектриком с ε = 2,0. Определите: а) модуль вектора элек­трического смещения |D|; б) заряд каждой пластины.
  

5.7.4. На рисунке показано распределение на-пряженности электростатического поля Е_х(х),созданного двумя параллельными заряженными бесконечными пластинами, вдоль направления х. Как различаются поверхностные плотности за­рядов σ₁и σ₂ на этих пластинах по знаку и по
модулю?

• 
  5
  
  .7.5. Изменится ли поток Ф_Е вектора напря­женности электростатического поля точечного заряда qчерез поверхность S, если заряд при­вести в движение, в направлении, указанном на рисунке? Заряд находится: а) внутри замкнутой
  поверхности; б) внутри незамкнутой поверхности. Площади поверхностей равны.
  
• 
  5
  
  .7.6. Используя принцип суперпозиции, найдите напряженность электростатического поля Е, которое создают в точке Aпараллельные равно­
  мерно заряженные с линейной плотностью за­ряда г = 2,0•10ˉ¹²Кл тонкие нити длинойl =1,0 м. Точка А находится, в одной плоскости с нитями и удалена от концов нитей на расстоя­ния 2а и а, как показано на рисунке (a = 0,40 м).
  

•




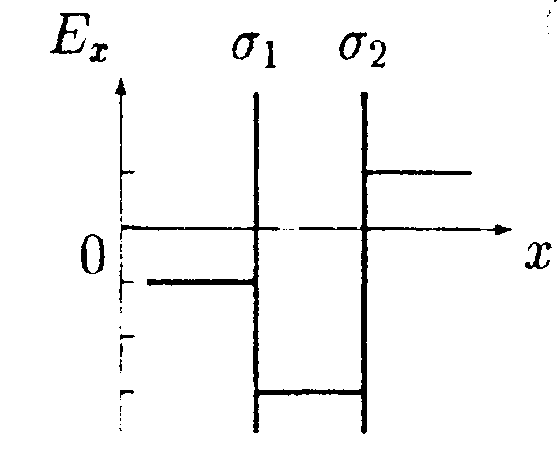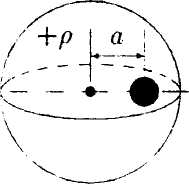5.7.7. В шаре, равномерно заряженном с объем­ной плотностью заряда +р, вырезана сферическая полость. Найдите напряженность электростатического поля внутри полости, если центр
ее удален на расстояние а от центра шара. Для нахождения поля используйте теорему Гаусса.

5.8. Вариант 8

5.8.1. Как будет вести себя незаряженный шар в каждом из электроста­тических полей, изображенных на рисунках а, б, в?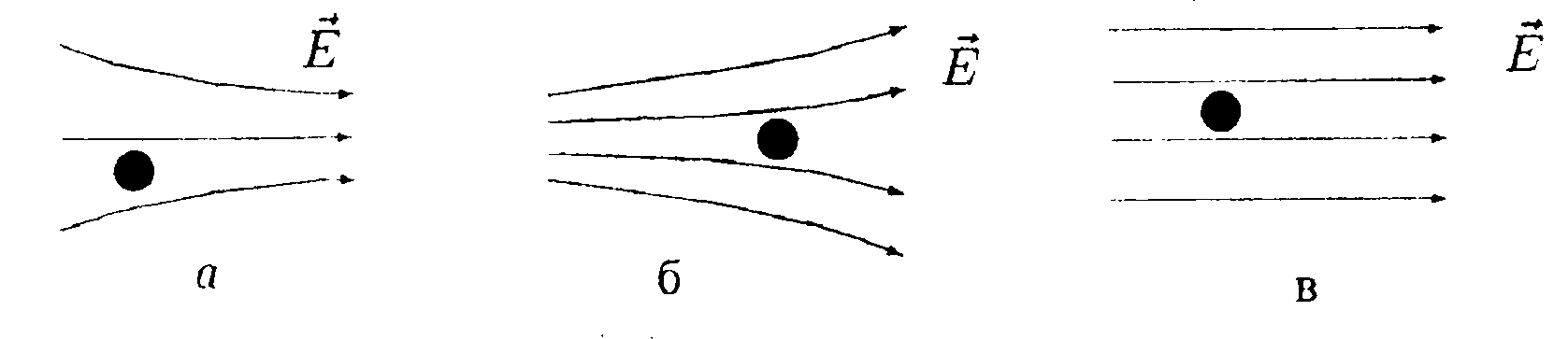

• 
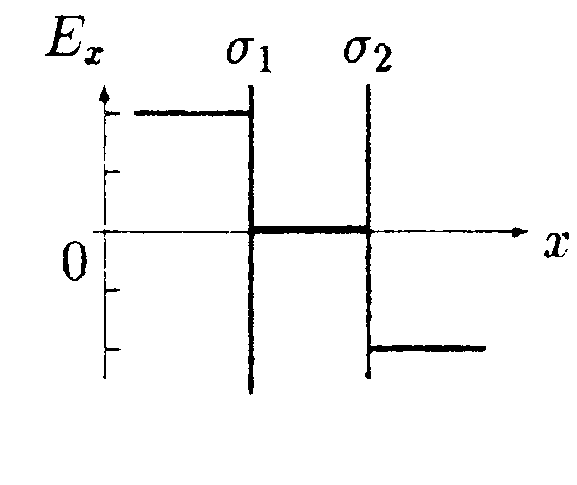  5.8.2. Два равных по величине заряда |q₁| = |q₂| = 3,0·10ˉ⁹ Кл рас­
  положены в вершинах острых углов равнобедренного прямоугольного
  треугольника на расстоянии l = 2,0 см. Определите, с какой силой оба
  заряда действуют на третий заряд q₃ = +1,0·10ˉ⁹ Кл, находящийся в
  вершине прямого угла треугольника. Рассмотрите случаи, когда пер­
  вые два заряда: а) одноименные; б) разноименные. Ответ поясните рисунками.
  
• 
  5.8.3. Три тонкие металлические пластины, расположенные параллельно друг другу, имеют заряды q, 2qи -3q.Расстояние между пластинами равно d, площадь каждой S. Определите силу, действующую на среднюю пластину, если dмного меньше линейных размеров пластин.
  

•

5.8.4. На рисунке показано распределение на­пряженности электростатического поля Е_х(х), созданного двумя параллельными заряженнымибесконечными пластинами, вдоль направления х. Как различаются поверхностные плотности за­рядов σ₁ и σ₂ на этих пластинах по знаку и по модулю?

• 
  5.8.5. В центре сферы радиусом R = 20 см находится точечный за­
  ряд Q = 10 нКл. Определите поток вектора напряженности электро­статического поля Ф_ечерез часть сферической поверхности площадью
  S = 20 см².
  
• 
  5.8.6. На тонкой пластинке, имеющей форму кольца с внутренним ра­диусом rи внешним R, равномерно распределен заряд q. Используя
  принцип суперпозиции, найдите зависимость напряженности электростатического поля Е(х) вдоль оси кольца, где х - расстояние от центра
  кольца. Постройте график зависимости Е(х). Анализируя зависимость
  Е(х), получите выражение для напряженности поля в случаях, когда
  а)r = 0 (диск); б) r≈ R(кольцо).
  

• 5.8.7. Две длинные тонкостенные коаксиальные трубки радиусами R₁ =
2,0 см и R₂ = 4,0см равномерно заряжены с линейными плотностями зарядов соответственно r₁ = +1,0 нКл/м и r₂ = -0,5 нКл/м. В пространстве между трубками - воздух. Определите напряженность электростатического поля в точках, находящихся на расстояниях 1,0 см, 3,0 см и 5,0 см от оси. Постройте график зависимости Е_г(r),где r - расстояние от оси трубок.

5.9 . Вариант 9

• 5.9.1. Между точечным зарядом +Qи бесконеч­ной пластиной, равномерно заряженной с поверх­ностной плотностью заряда -σ, находится ди­поль. В каком направлении он будет двигаться?

• 
  5.9.2. Три одинаковых положительных заряда величиной qкаждый рас­
  положены в вершинах равностороннего треугольника со стороной а.
  Какой отрицательный заряд Qнадо поместить в центре треугольника,
  чтобы система из четырех зарядов находилась в равновесии?
  
• 
  5.9.3. Электростатическое поле образовано положительно заряженной
  бесконечно длинной нитью. Протон, двигаясь под действием этого поля
  от точки, находящейся на расстоянии х1= 1,0 см от нити, до точки
  x2= 4,0 см, изменил свою скорость от 2,0-10⁵ до 3,0·10⁶м/с. Найдите
  линейную плотность заряда нити т. Масса протона m = 6,67·10ˉ²⁷кг.
  

•

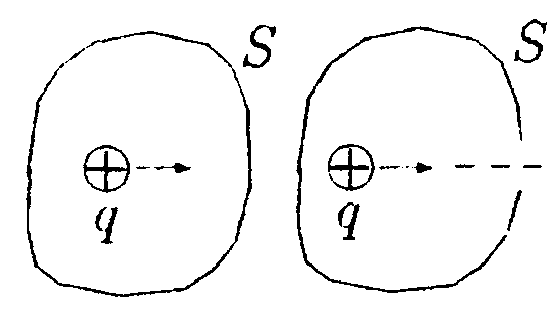
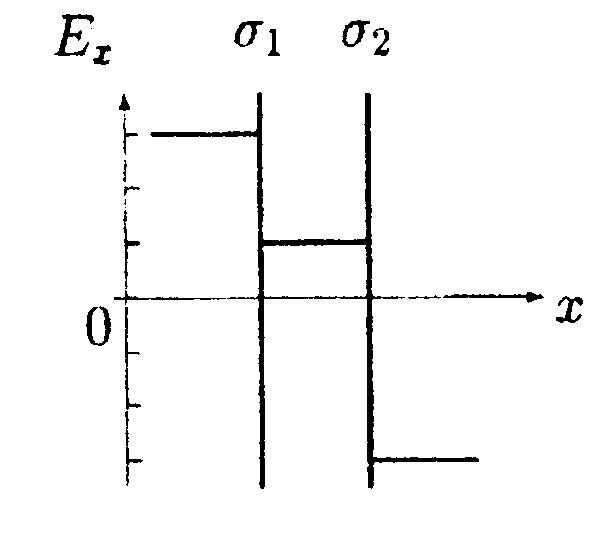5.9.4. На рисунке показано распределение напряженности электростатического поля Е_х{х),
созданного двумя параллельными заряженными
бесконечными пластинами, вдоль направления х.
Как различаются поверхностные плотности за­
рядов σ1и σ2на этих пластинах по знаку и по
модулю?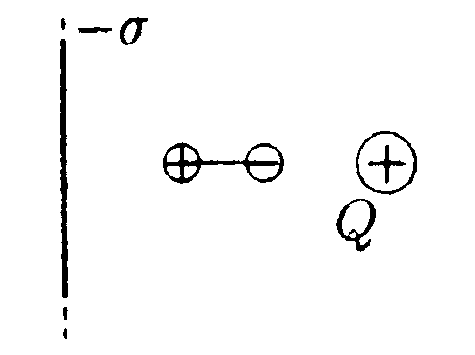

•

5.9.5. На рисунках изображены линии напряженности электростати­ческих полей. Определите знаки потоков векторов напряженности ФE
через замкнутые поверхности S. сечения которых показаны на рисун­ках а,б,в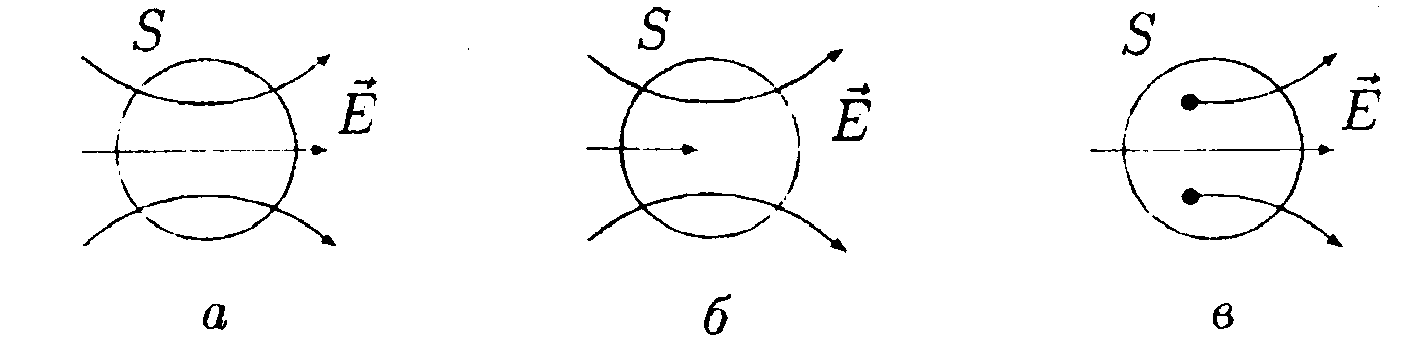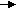

•

5.9.6. По дуге, длина которой равна ⅔ длины окружности радиусом R = 10 см, равномерно распределен заряд с линейной плотностью г = 0,2 мкКл/м. Используя принцип суперпозиции, определите напря­женность электростатического поля Е в центре кривизны дуги.

•5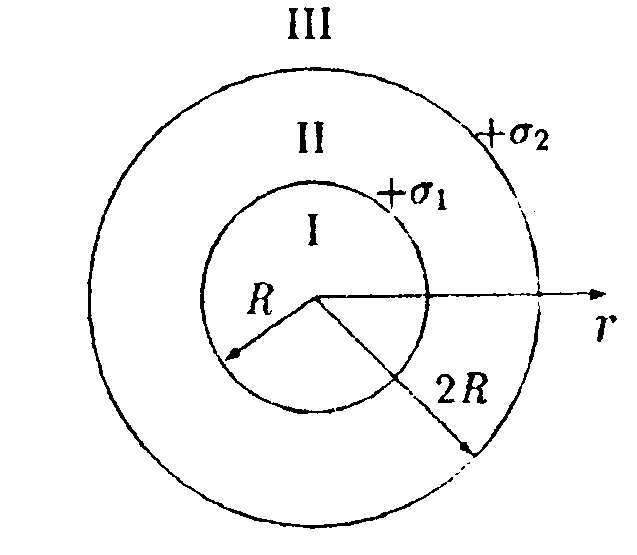

.9.7. На двух концентрических сферах радиу­сами Rи 2Rравномерно распределены заряды с поверхностными плотностями σ1=4σ и σ2=σ, где σ = +30 нКл/м². Используя теорему Гаусса, найдите зависимость напряженности электро­статического поля Е от расстояния г для трех областей I, II, III (г - расстояние от центра сфер).

•5.10 . Вариант 10

•5.10.1. На рисунках а,) б), в) показаны линии напряженности элек­тростатических полей. Сравните величины напряженности в точках 1, 2, 3.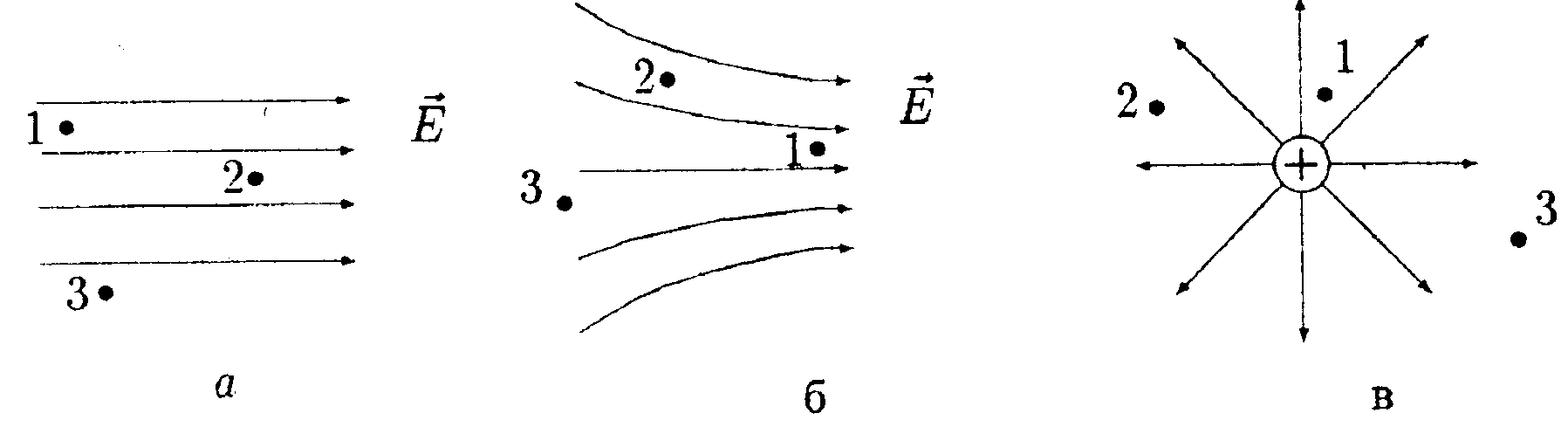

•

5.10.2. Два шарика массой m = 1,0 г каждый подвешены на нитях, верх­ние концы которых соединены вместе. Длина каждой нити l= 1,0 см. Какие одинаковые заряды необходимо сообщить шарикам, чтобы нити разошлись на угол a = 60°?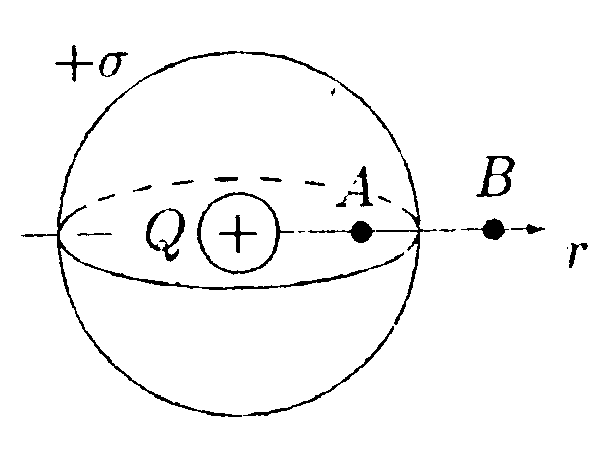



•5.10.3. Точечный заряд Q = +3,0 · 10ˉ⁵Кл, на­ходится в центре сферы радиусом R = 20см, равномерно заряженной с поверхностной плотно­стью заряда σ = +2,0·10ˉ⁵Кл/м². Найдите силу, действующую на заряд q = +2,0 • 10ˉ⁹Кл, кото­рый последовательно помещают сначала в точку A. а затем в точку В. Точка А находится на рас­стоянии га= 16 см от центра сферы, а точка В на расстоянии r_в= 30см. Изобразите графи­чески зависимость Е{r), где r - расстояние от центра сферы.

• 5.10.4. На рисунке показано распределение напряженности электростатического поля Е_х(х),
созданного двумя параллельными заряженными
бесконечными пластинами, вдоль направления х.
Как различаются поверхностные плотности за­
рядов σ1и σ2 на этих пластинах по знаку и по
модулю?

5.10.5. Равномерно заряженную плоскость с поверхностной плотностью заряда а = +10 нКл/м² пересекает сфера, центр которой лежит на плос­кости. Поток вектора напряженности поля Е через сферу ФE= 3,2 Вм. Определите радиус сферы.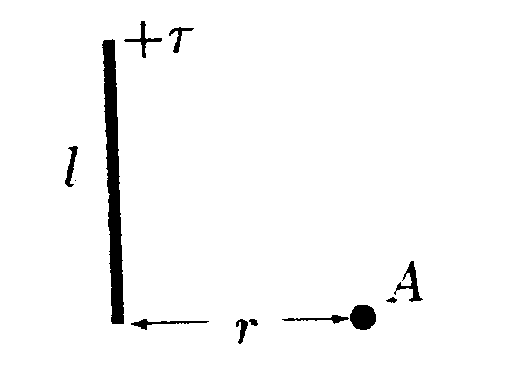

•

5.10.6. Тонкий стержень длиной I =10 см заряжен с линейной плотностью заряда r=400 нКл/м. Используя принцип суперпозиции, найдите напряженность электростатического поля Е в точке А, которая удалена от конца стержня на расстояние г = 8,0 см перпендику­лярно стержню.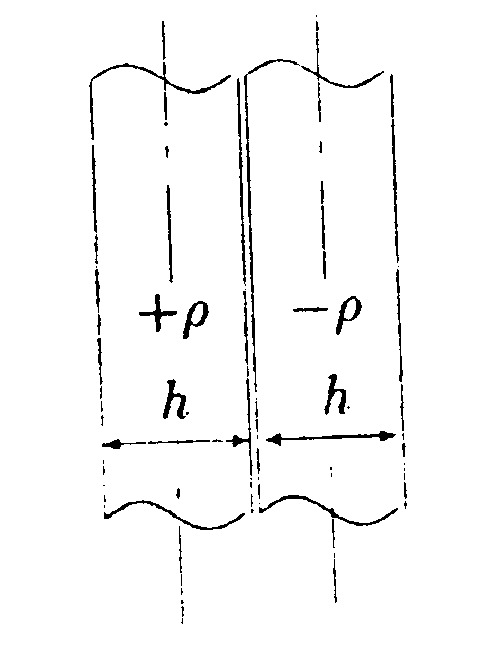

•

5.10.7. Две бесконечные пластины толщиной hзаряжены равномерно по объему и сложены вме­сте. Объемная плотность заряда первой пла­стины +р, а второй -р. Используя теорему Гаусса и учитывая симметрию поля каждой пла­стины относительно ее центральной плоскости, найдите максимальную напряженность Е суммарного электростатического поля пластин.

5.11. Вариант 11

•5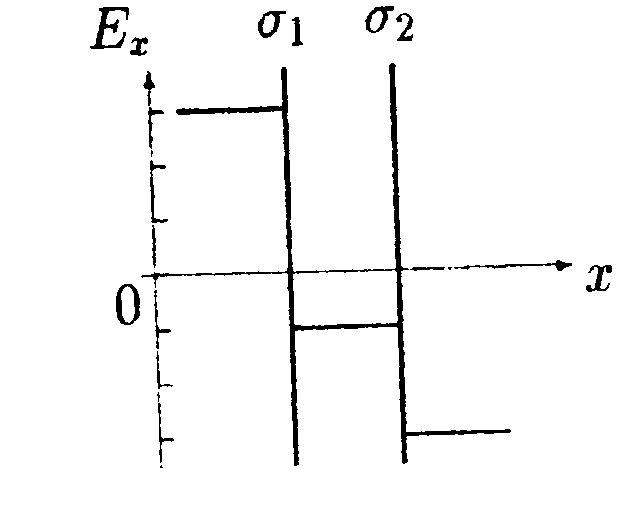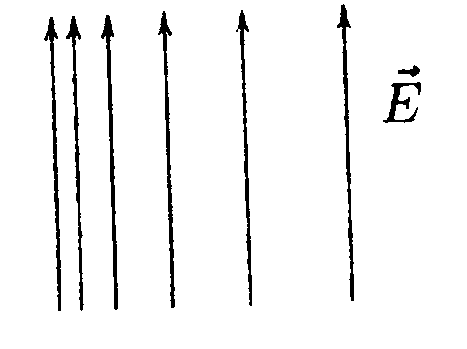



.11.1. Возможно ли существование электроста­тического поля, изображенного на рисунке?

• 
  5.11.2. В вершинах шестиугольника со стороной а = 10 см расположены
  точечные заряды q, 2q, 3q, 4q, 5q, 6q (q= 0,10 мкКл). Найдите силу,
  действующую на точечный заряд q, лежащий в плоскости шестиугольника и равноудаленный от его вершин.
  
• 
  5.11.3. Два взаимно перпендикулярных бесконечных провода, равно­
  мерно заряженных с линейными плотностями заряда r₁и r₂, находятся
  на расстоянии а друг от друга. Как зависит сила взаимодействия
  проводников от расстояния между ними?
  

•

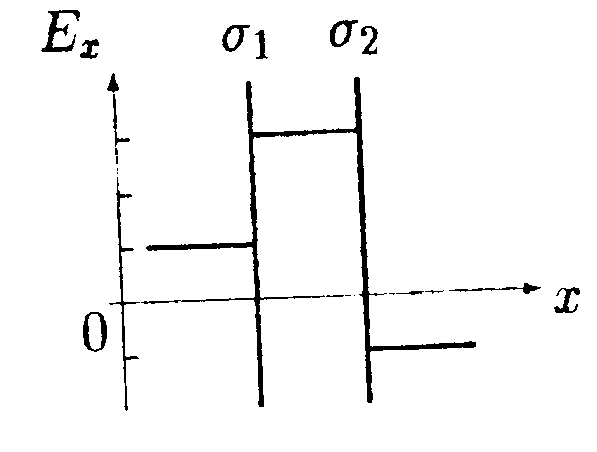5.11.4. На рисунке показано распределение на­пряженности электростатического поля Е_х(х), созданного двумя параллельными заряженными бесконечными пластинами, вдоль направления х. Как различаются поверхностные плотности за­рядов σ₁ и σ₂на этих пластинах по знаку и по модулю?

• 
  5.11.5. Бесконечно длинный цилиндр радиусом R = 0,10 м равномерно
  заряжен с поверхностной плотностью заряда а = +1,0 • 10^-10Кл/м².
  Определите поток вектора напряженности Е через коаксиальную цилиндрическую поверхность единичной длины, если радиус этой цилиндрической поверхности: а) r < R; б) r > R.
  
• 
  5.11.6. Тонкое кольцо радиусом R равномерно заряжено с линейной
  плотностью заряда г. Используя принцип суперпозиции, найдите напряженность электростатического поля: а) в центре кольца; б) в точке,
  расположенной на оси кольца на расстоянии hот его центра.
  
• 
  5.11.7. Шаровому проводнику радиусом R₁сообщили заряд Q. Используя теорему Гаусса, получите выражение для расчета напряженности Е
  и смещения Dэлектростатического поля, созданного этим зарядом, если
  проводник окружен прилегающим к нему концентрическим слоем одно­
  родного диэлектрика с диэлектрической проницаемостью е и внешним
  радиусом R₂Нарисуйте линии напряженности и электрического сме­щения. Постройте графики зависимости Е(r) и D(r), где r - расстояние
  от центра шара.
  

5.12 . Вариант 12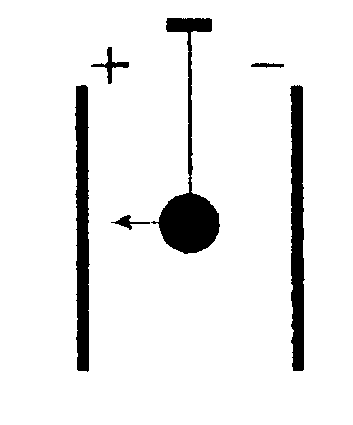

•

5.12.1. Между двумя разноименно заряженными
пластинами с равными по модулю зарядами помещен незаряженный металлический легкий шарик на шелковой нити, как показано на рисунке. Что будет происходить с шариком, если его привести в движение в направлении, указан­ ном стрелкой?

• 
  5.12.2. Два одинаковых положительных заряда q1 = q2 = +1,б ·10ˉ¹⁹Кл
  расположены на расстоянии l = 2,0·10ˉ¹⁰м друг от друга. Вдоль перпендикуляра, проходящего через середину отрезка, соединяющего эти за­
  ряды, движется электрон. В какой точке этого перпендикуляра сила вза­имодействия электрона и системы неподвижных зарядов максимальна?
  
• 
  5.12.3. Между пластинами плоского воздушного конденсатора находится точечный заряд q =30 нКл. Поле конденсатора действует на заряд с силой F = 10 мН. Определите силу взаимного притяжения пластин, если площадь каждой пластины S = 100 см².
  

• 
  5
  
  .12.4. На рисунке показано распределение напряженности электростатического поля Е_х(х),
  созданного двумя параллельными заряженными
  бесконечными пластинами, вдоль направления х.
  Как различаются поверхностные плотности за­
  рядов σ1и σ2 на этих пластинах по знаку и по
  модулю?
  
• 
  5
  
  .12.5. Пластины плоского конденсатора равно­
  мерно заряжены с поверхностной плотностью за­
  ряда |σ| = 200 нКл/м². Пространство между пла­стинами заполнено двумя слоями диэлектрика
  с относительными диэлектрическими проницаемостями ε1= 3,0 и ε2 = 5,0. Найдите поток
  вектора электрического смещения Dи поток вектора напряженности Е через цилиндр с площадью основания S = 10 см².
  

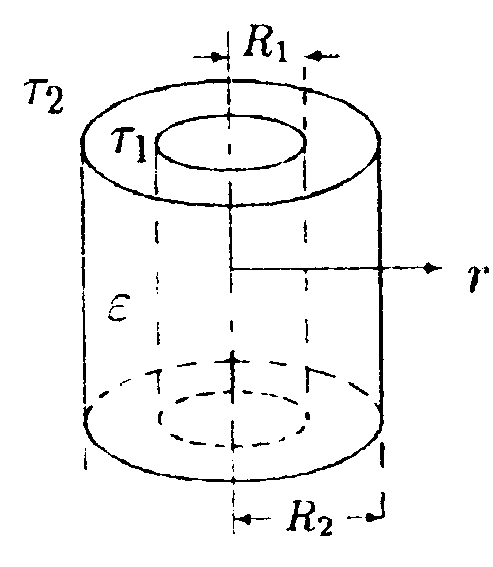• 5.12.6. Две длинные тонкостенные коаксиальные трубки радиусами R1и R2 равномерно заряжены с линейными плотностями зарядов +r1 и +r2. Ис­пользуя принцип суперпозиции, найдите зависи­мость напряженности электростатического поля Е(r), где r - расстояние от оси трубок.

• 5.12.7. Шар радиусом R равномерно заряжен с объемной плотностью заряда +р. Используя теорему Гаусса, найдите зависимость напряжен­ности электростатического поля Е и электрического смещения Dот расстояния г, отсчитываемого от центра сферы. Постройте графики за­висимости Е(r) и D(r). Диэлектрическая проницаемость шара равна е.