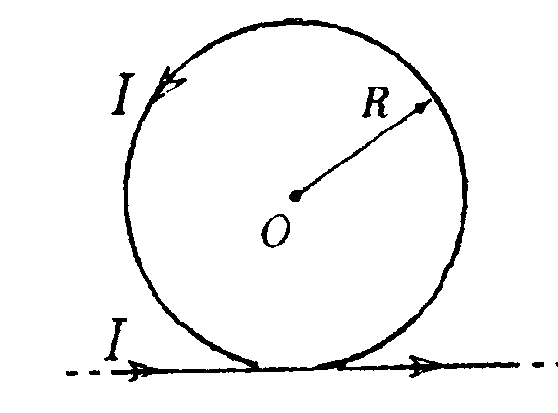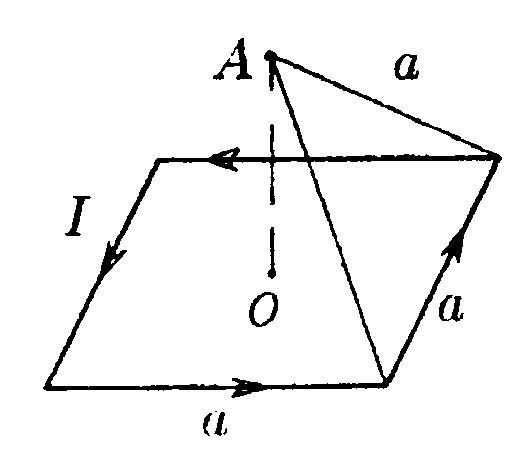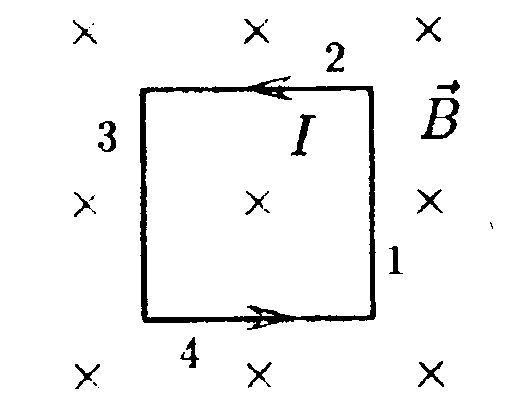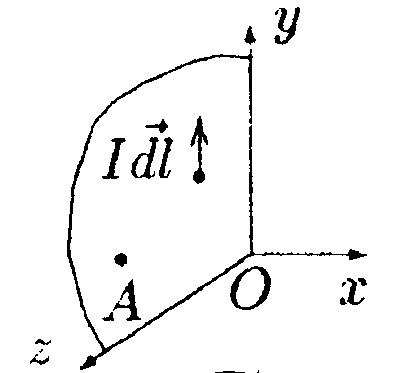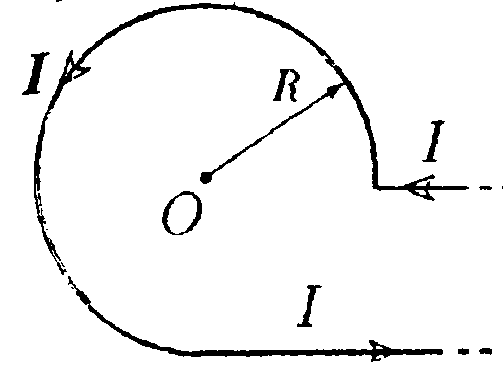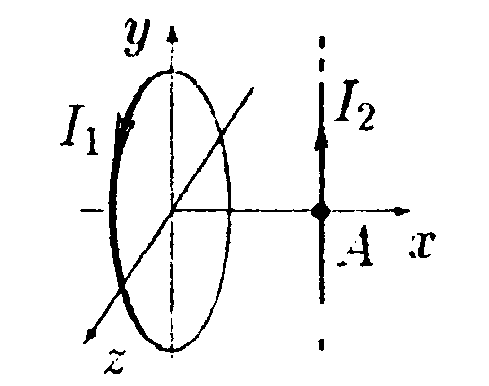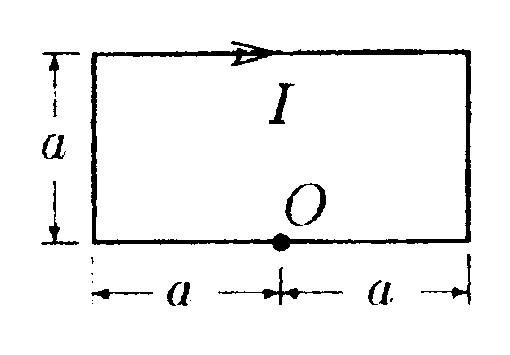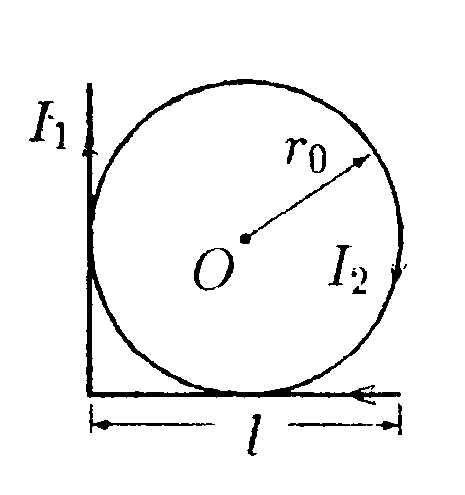Часть II Электричество и магнетизм. Сборник задач по общей физике Часть II. Электричество и электромагнетизм Под ред. Э. Б. Селивановой Библиотека Ново иб и, с ко го
 Скачать 40.78 Mb. Скачать 40.78 Mb.
|
|
7.7. Вариант 7
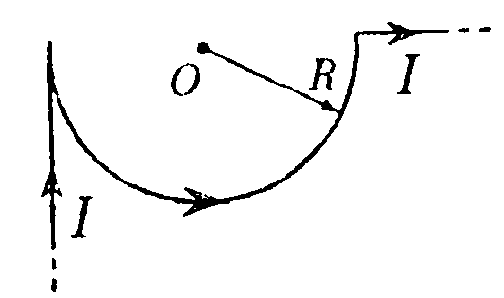
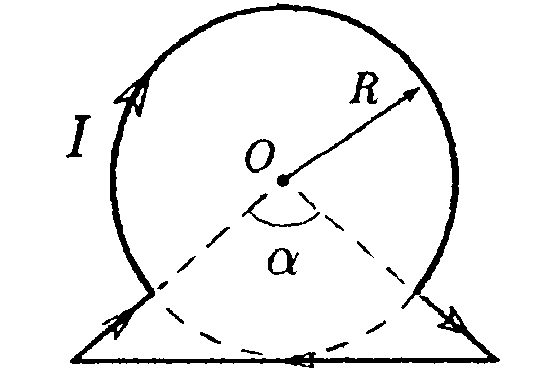
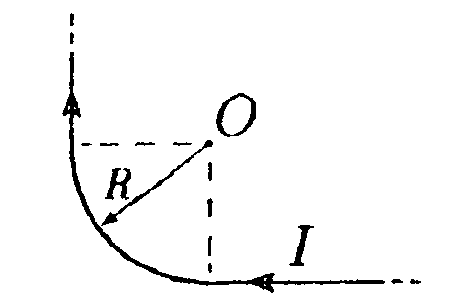
7.8 . Вариант 8 • 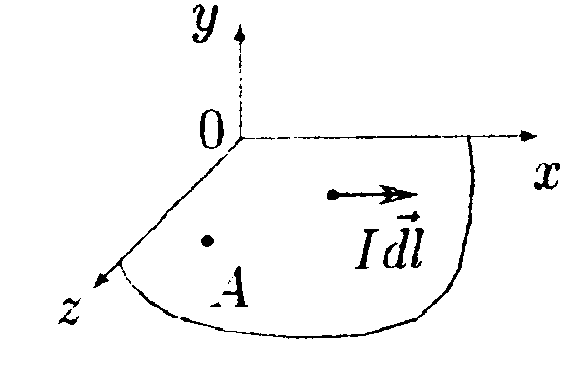 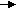  7.8.1. Укажите направление вектора индукции 7.8.1. Укажите направление вектора индукциимагнитного поля dB, созданного в точке А элементом тока Idl, если точка А и элемент тока Idlрасположены в плоскости xOz. • 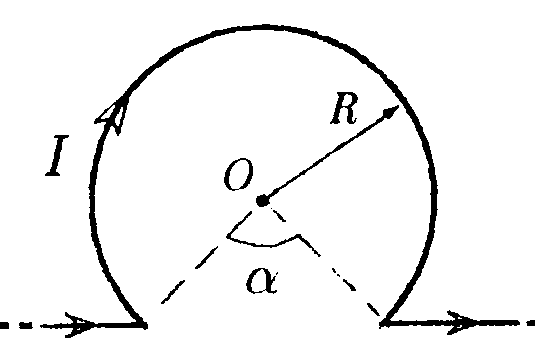 7.8.2. Бесконечно длинный тонкий проводник с током Iимеет изгиб (плоскую петлю) радиусом R. Определите индукцию магнитного поля, созданного током в точке О (а =2π/3).
7.8.4. По двум длинным параллельным проводам текут токи в противоположных направлениях. Токи I1 = I2 = I = 10 А. Расстояние между проводами d = 0.30 м. Определите магнитную индукцию в точке A, удаленной от первого и второго проводов соответственно на расстояние r1= 0.15 м, r2 = 0,20 м. • 7.8.5. В каком из указанных случаев циркуляция вектора индукции вдоль замкнутого контура Lнеравна нулю? 7.8.6. Катушка длиной l= 20 см содержит N = 100 витков. По обмотке катушки идет токI= 5,0 А. Диаметр dкатушки равен 20 см. Определите магнитную индукцию В в точке, лежащей на оси катушки на расстоянии b= 10 см от ее конца. 7 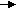  .9 • Вариант 9
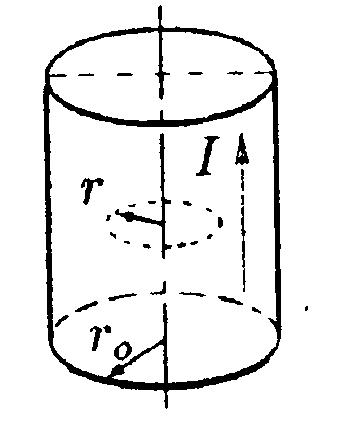
7.9.3. Два прямолинейных длинных параллельных проводника находятся на расстоянии d1= 10 см друг от друга. По проводникам течет ток в одном направлении 11 = 20 А и 12= 30 А. Какую работу надо со вершить, чтобы раздвинуть эти проводники до расстояния d2 = 20 см. Расчет произведите на единицу длины проводника. • 7.9.4. По проводнику, согнутому в виде квадрат ной рамки со стороной а = 10 см, течет ток I= 5,0 А. Определите индукцию магнитного поля В в точке А, равноудаленной от вершин квадрата на расстояние, равное длине его стороны. • 7.9.5. По медному проводу круглого сечения (R= 2,0 см) течет ток I= 500 А. Определите индукцию магнитного поля В внутри провода в точке, отстоящей на расстоянииr = 0,5 см от оси провода. • 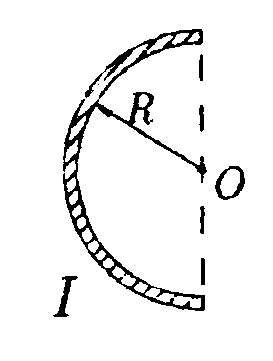 7.9.6. Ток I= 200 А течет (от нас) по длин ному прямому проводнику, сечение которого имеет форму тонкого полукольца радиусом R =10см. Найдите индукцию магнитного поля В в точке О. 7.10 . Вариант 10
• 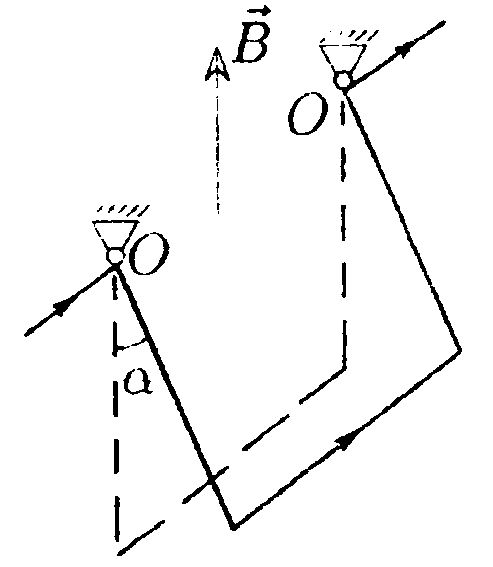 7.10.3. Медный провод с сечением S = 2,0 мм2. согнутый в виде трех сторон квадрата, может вращаться, как показано на рисунке, около горизонтальной оси ОО. Провод находится в однородном магнитном поле, направленном вертикально. Когда по проводу идет ток I = 10 А, провод отклоняется от положения равновесия на угол а = 15°. Определите индукцию магнитного поля В. • 7.10.4. По плоскому контуру из тонкого провода течет ток I= 100 А. Определите магнитную индукцию В поля, создаваемого этим током в точке О. Радиус Rизогнутой части контура равен 20 см, (α = 2π/3). 7.10.5. Вычислите циркуляцию вектора индукции вдоль контура, охватывающего токи I1= 10 А, I2=15 А. текущие в одном направлении, и ток Iз = 20 А, текущий в противоположном направлении. •    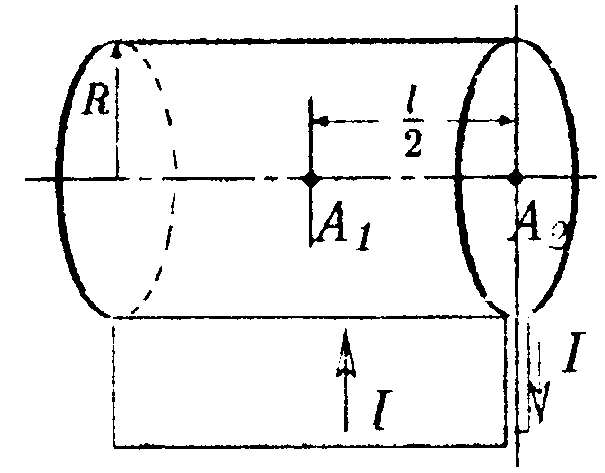 7.10.6. Тонкая лента шириной l свернута в трубку радиусом R. По ленте течет равномерно распределенный по ее ширине ток I. Точечный магнитный диполь с магнитным моментом Рт. первоначально находившийся на оси трубки в ее середине (точка A1), перемещается вдоль оси в точку А2 так, что вектор Ртостается параллельным вектору В. Определите работу, совершенную при перемещении диполя. 7.11. Вариант 11
•7.11.4. Два параллельных бесконечно длинных провода, по которым те кут токи I = 60 А в одном направлении, расположены на расстоянии d = 10 см друг от друга. Определите индукцию магнитного поля в точке, отстоящей от одного проводника на расстоянии r1= 5,0 см, от другого на расстоянии r2= 12 см. • 7.11.5. Ток I течет по длинному прямому про воду, перпендикулярному проводящей плоскости, и растекается по ней. Определите распределение магнитного поля В над плоскостью и под ней, используя закон полного тока. • 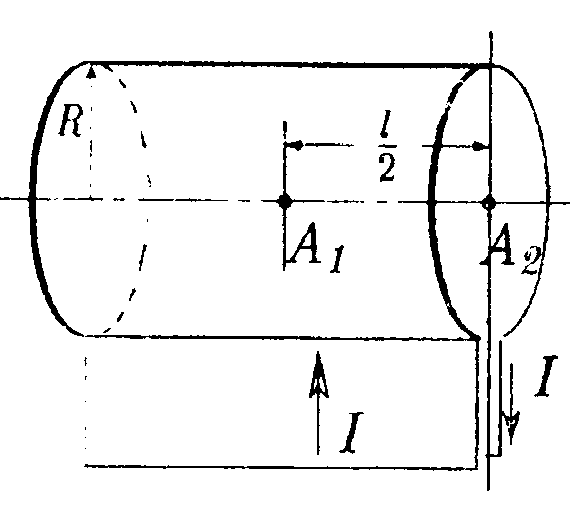 7.11.6. Тонкая лента ширинойl= 40 см свернута в трубку радиусом R= 30 см. По ленте течет равномерно распределенный по ее ширине ток I = 200 А. Определите магнитную индукцию В на оси трубки в двух точках: 1) в средней точке A1; 2) в точке А2, совпадающей с концом трубки. 7.12. Вариант 12 • 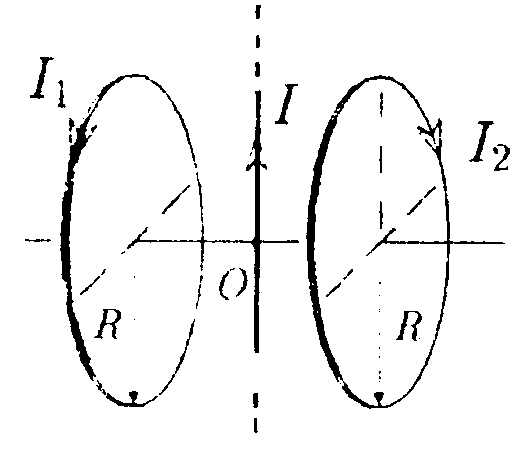 7.12.1. Бесконечно длинный провод с током Iнаходится на одинаковом расстоянии от двух круговых токов (I1= I2 = I), радиусом R. Определите направление силы Ампера, действующей на провод с током I в точке О. • 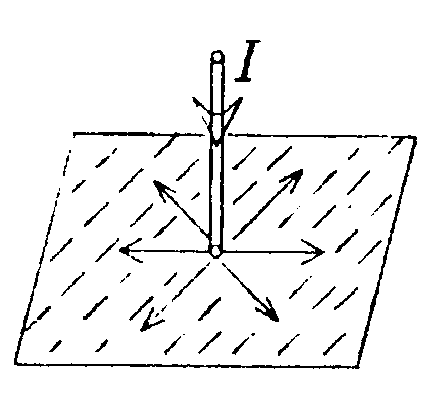 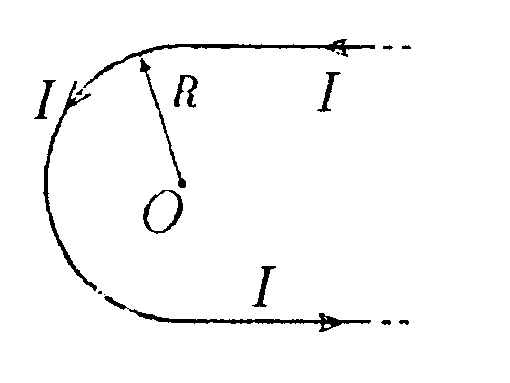 7.12.2. Бесконечно длинный тонкий проводник с током I имеет изгиб (плоскую петлю) радиусом R. Определите индукцию магнитного поля, созданного током в точке О. 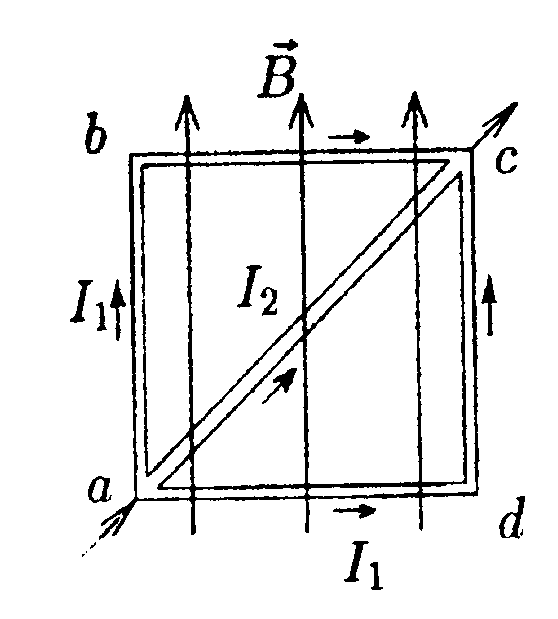 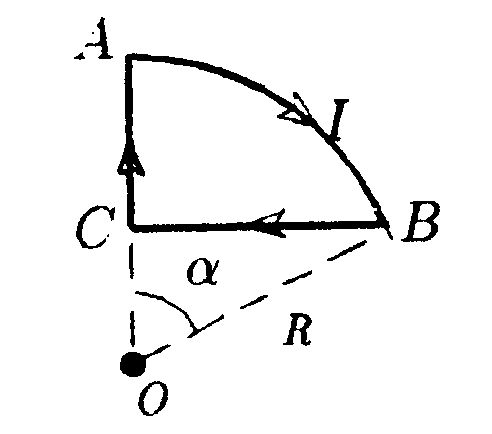 • 7.12.3. Контур, представляющий собой квадрат с диагональю, изготовлен из медной проволоки сечением 1 мм2 и подключен к источнику постоянного напряжения 110 В (в точках а и с). Плоскость квадрата расположена параллельно магнитному полю с индукцией В = 17.10ˉ4Тл. Определите величину и направление результирующей силы, действующей со стороны поля на контур. Удельное сопротивление меди р = 1,7·10ˉ8Ом·м. • 7.12.4. По контуру ABC, изображенному на рисунке, течет ток I = 10 А. Определите магнитную индукцию в точке О, если радиус дуги АВ R=10 см, а = 60°.
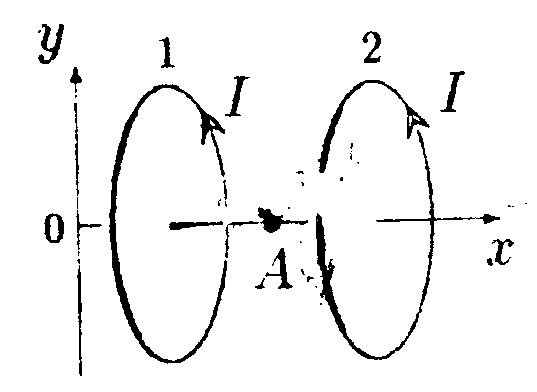
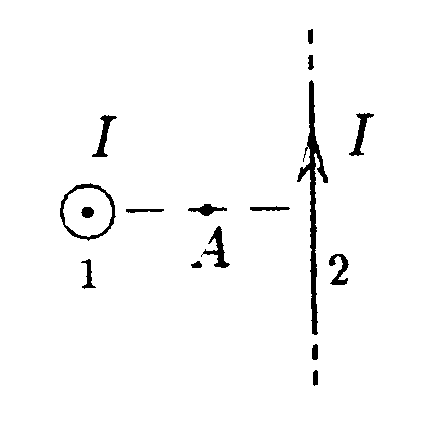
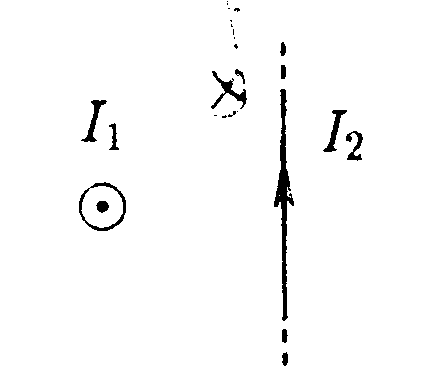
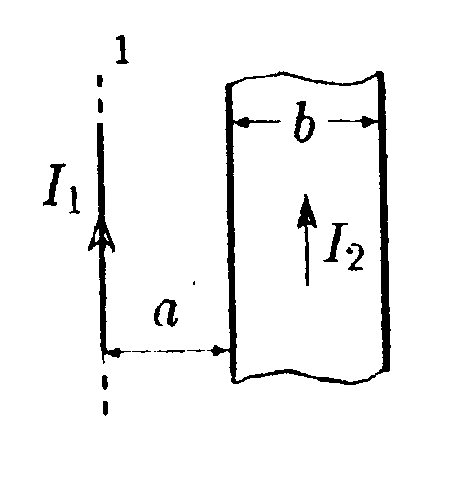
7.13 . Вариант 13 • 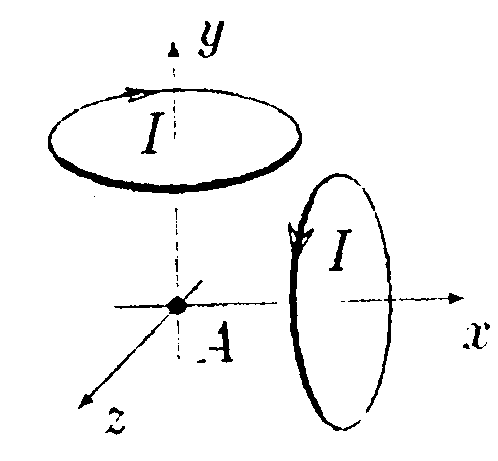 7.13.1. Поле создано двумя круговыми токами I, равными по величине. Определите направление вектора индукции В в точке А. расположенной относительно токов на одинаковом расстоянии. 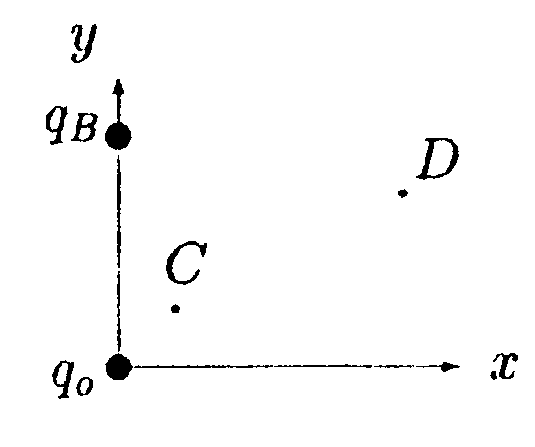 • 7.13.2. Возле бесконечного прямолинейного проводника 1 с током I расположен подвижный прямолинейный конечной длины проводник АВ. Проводник АВ лежит в плоскости, проходящей через проводник 1 и перпендикулярен ему. Что будет происходить с проводником АВ, если по нему пропустить ток Iв направлении, указанном стрелкой? 7.13.3. Два прямолинейных длинных параллельных проводника находятся на некотором расстоянии друг от друга. По проводникам текут токи, равные по величине и по направлению. Найдите силу тока I, текущего по каждому из проводников, если известно, что для того, чтобы раздвинуть эти проводники на расстояние вдвое большее, пришлось со вершить работу (на единицу длины проводника), равную 5,5·10ˉ7Дж/см. • 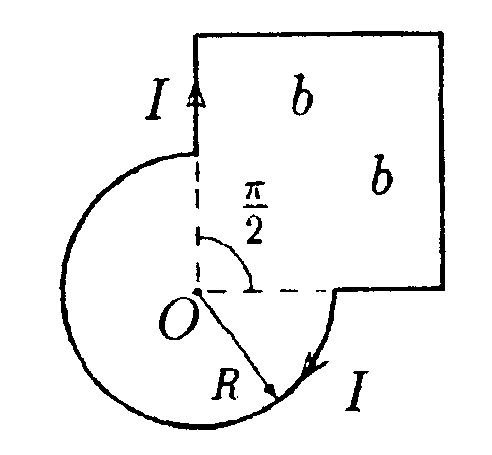 7.13.4. Найдите индукцию магнитного поля в точке О контура с током I = 10 А, который показан на рисунке. Радиус Rи сторона bизвестны: R= 10 см, b= 20 см. • 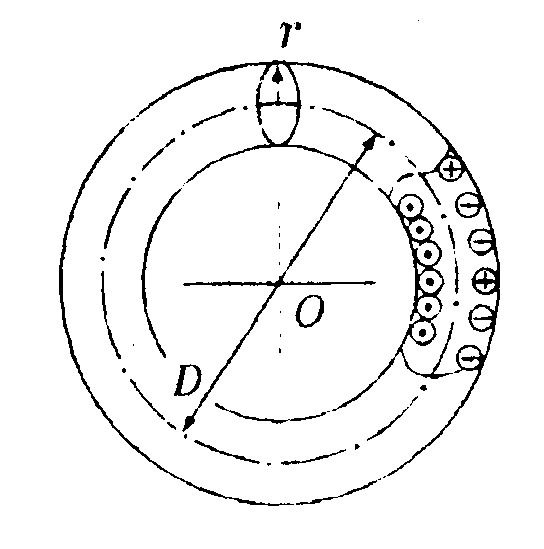 7.13.5. Диаметр тороида без сердечника по сред ней линии равен D= 30 см. В сечении тороид имеет круг радиусом r= 5,0 см. По обмотке тороида. содержащей N = 2000 витков, течет ток I = 5,0 А. Пользуясь законом полного тока, определите максимальное и минимальное значение магнитной индукции В в тороиде. • 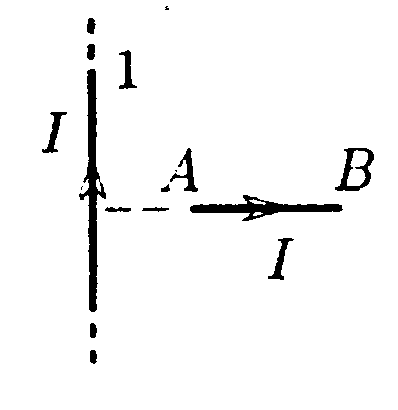 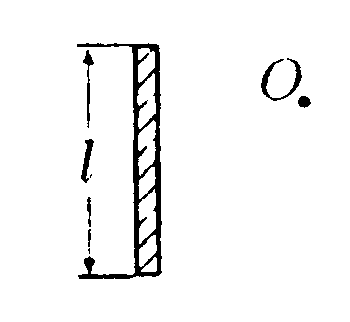 7.13.6. По тонкой прямой бесконечной ленте шириной lтечет ток I (от нас). Рассчитайте индукцию магнитного поля этого тока в произвольной точке О. На рисунке показано сечение ленты. 7.14 . Вариант 14
• 7.14.6. Очень длинный прямой соленоид имеет радиус сечения R и число витков п на единицу длины. По соленоиду течет постоянный токI. Найдите индукцию магнитного поля В на оси как функцию х, где х - расстояние, отсчитываемое вдоль оси соленоида от его торца. Изобра- зите примерный график зависимости индукции В от отношения x/R. |