Часть II Электричество и магнетизм. Сборник задач по общей физике Часть II. Электричество и электромагнетизм Под ред. Э. Б. Селивановой Библиотека Ново иб и, с ко го
 Скачать 40.78 Mb. Скачать 40.78 Mb.
|
|
Министерство общего и профессионального образования Российской Федерации НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ 53 С 232 Сборник задач по общей физике Часть II. Электричество и электромагнетизм Под ред. Э.Б. Селивановой Б  иблиотека Ново иб>и, с ко го .гг^л. хни'-: с ноге •'Нот тут, иблиотека Ново иб>и, с ко го .гг^л. хни'-: с ноге •'Нот тут,Новосибирск 1998 53 (076.1)+ 537 (076.1) 15ВЫ 5-7782-0193-1 Составители: Э.Б. Селиванова, СИ. Вашуков, Л.М. Родникова, Н.Я. Усольцева, Б.И. Юдин Рецензенты: А.Н. Лузин, канд. физ.-мат. наук, проф. В.Я. Чечуев, канд. техн. наук, доц. Работа подготовлена на кафедре общей физики 15ВК 5-7782-019. © Новосибирский государственный технический университет. 1998 г. Содержание 5 . Тема: Закон Кулона. Теорема Гаусса................................. 7
5.3. Вариант 3 10 5.4 . Вариант 4 11 5.5.Вариант 5 12 5.6.Вариант 6 ... 14 5.7.Вариант 7 15
6 . Тема: Потенциал. Работа. Энергия электрического поля , . , 32
6.9. Вариант 9 41 6.10. Вариант 10 42 6.11. Вариант 11 43 6.12 .Вариант 12 44 6.13.Вариант 13 45 6.14.Вариант 14 46 6.15.Вариант 15 48
7 .Тема: Магнитное поле в вакууме ...............................................................54 7.1 . Вариант 1 54 7.2 Вариант 2 55 7.3 Вариант 3 56
7.6 Вариант 6 59 7.7. Вариант 7 60
7.11. Вариант 11 64 7.12. Вариант 12 65 7.13. Вариант 13 66 7.14. Вариант 14 68 7.15. Вариант 15 69 7.16. Вариант 16 70 7.17. Вариант 17 71 7.18. Вариант 18 72 8. Тема: Сила Лоренца. Электромагнитная индукция ................................. 74 8.1 Вариант 1 74 8.2 Вариант 2 75 8.3. Вариант 3 76 8.4Вариант 4 77 8.5. Вариант 5 79 8.6. Вариант 6 80 8.7. Вариант 7 81 8.8 . Вариант 8 82 8.9. Вариант 9 83 8.10. Вариант 10 84 8.11.Вариант 11 86 8.12.Вариант 12 87 8.13.Вариант 13 88 8.14.Вариант 14 89 8.15.Вариант 15 91 8.16.Вариант 16 92 8.17. Вариант 17 93 .18. Вариант 18 95 Предисловие Авторы стремились создать сборник задач, с помощью которого можно реализовать индивидуальную работу студентов. Данный сборник задач соответствует учебной программе по курсу общей физики в техническом университете. Первая часть сборника задач по разделу «Механика» вышла в свет в 1996 г. Во вторую часть, входят 4 темы разделов курса общей физики «Электростатика» и «Электромагнетизм» (нумерация тем сквозная в первой и второй частях сборника задач).
В каждой теме по 18.примерно,одинаковых по сложности вариантов специально подобранных задач. При их составлении учитывались результаты психолого-педагогического анализа процесса решения физических задач, выполненного как составителями, так и другими авторами. Предварительно была проделана большая работа по выделению основных типов задач. Большая часть их уже публиковалась в методических работах «Варианты задач для индивидуальных заданий», от которых содержание данного сборника отличается большим числом вариантов и тщательностью отработки каждого из них, т.е. в каждом варианте еще раз продумана последовательность задач и иерархия их сложности, откорректированы условия задач и рисунки, заменены неудачные задачи и т.д. В результате в каждом варианте:
Такое построение вариантов, как показывает наш опыт, позволяет продуктивно работать студентам различного уровня подготовленности. В сборнике не приводятся примеры решения задач и не даются ответы, так как задачник предполагается использовать также на коллоквиумах и экзаменах. На текущих же занятиях преподаватель выдает лист ответов по данной теме, и каждый студент может проверить правильность своего ответа. Наиболее эффективно следует использовать этот задачник совместно со специально разработанными для него методическими указаниями:
В них в краткой наглядной форме (в виде таблиц и блок-схем) изложена теория, дана классификация задач, их алгоритмы, а также примеры решения задач всех типов, выделенных в данной теме. На основе этих примеров могут быть решены и задачи других вариантов. Совместное использование названных выше работ позволяет организовать любые формы обучения и применять их как на практических занятиях, так и для самостоятельного изучения физики. Э.Б. Селиванова 5 . Тема: Закон Кулона. Теорема Гаусса 5.1. Вариант 1  • 5.1.1. На некотором расстоянии друг от друга в точках О и Внаходятся два одинаковых по модулю точечных заряда. На рисунке показано пространственное распределение напряженности электростатического поля между зарядами Е(г).Определите знаки зарядов.
5 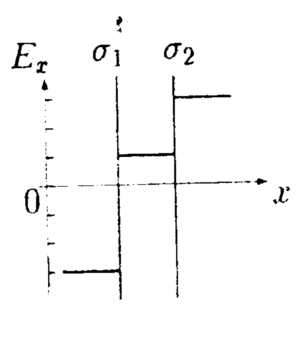 .1.4. На рисунке показано распределение напряженности электростатического поля Ех(х),созданного двумя параллельными заряженными бесконечными пластинами, вдоль направления x. Как различаются поверхностные плотности зарядов σ1и σ2на этих пластинах по знаку и по модулю? .1.4. На рисунке показано распределение напряженности электростатического поля Ех(х),созданного двумя параллельными заряженными бесконечными пластинами, вдоль направления x. Как различаются поверхностные плотности зарядов σ1и σ2на этих пластинах по знаку и по модулю?
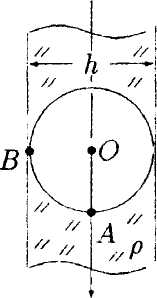 • 5.1.7. В бесконечной пластине, равномерно заряженной с объемной плотностью заряда ρ, вырезали сферическую полость так, как показано на • 5.1.7. В бесконечной пластине, равномерно заряженной с объемной плотностью заряда ρ, вырезали сферическую полость так, как показано нарисунке. Толщина пластины h. Используя теорему Гаусса и учитывая симметрию поля относительно центральной плоскости пластины, найдите: а) напряженность электростатического поля в точках А и В; б) зависимость напряженности поля Е(г), где г – расстояние от точки О. 5.2. Вариант 2 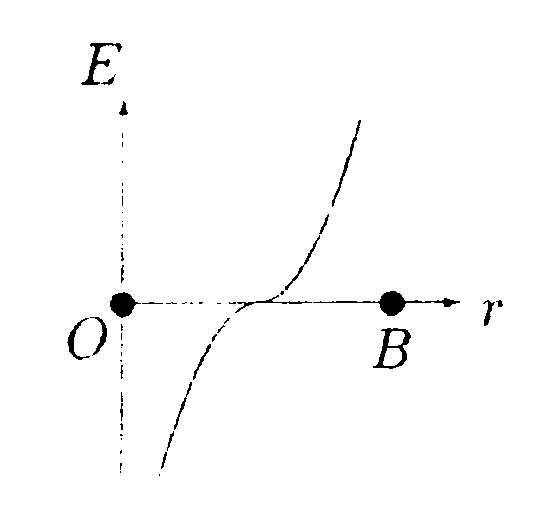 • 5.2.1. На некотором расстоянии друг от друга в точках О и Внаходятся два одинаковых по модулю точечных заряда. На рисунке показано распределение напряженности электростатического поля между зарядами Е(г). Определите знаки зарядов. • 5.2.2. Отрицательный заряд q1=-5qи положительный q2 = +2qзакреплены на расстоянии r друг от друга. Где на линии, соединяющей заряды, следует поместить положительный заряд Q, чтобы он находился в равновесии. • 5.2.3. Параллельно бесконечной плоскости, заряженной с поверхностной плотностью заряда σ= 4,0 мкКл/м2, расположена бесконечно длинная прямая нить, заряженная с линейной плотностью заряда τ = 100 нКл/м2. Определите силу F, действующую со стороны плоскости на отрезок нити, длиной L = 1,0 м. 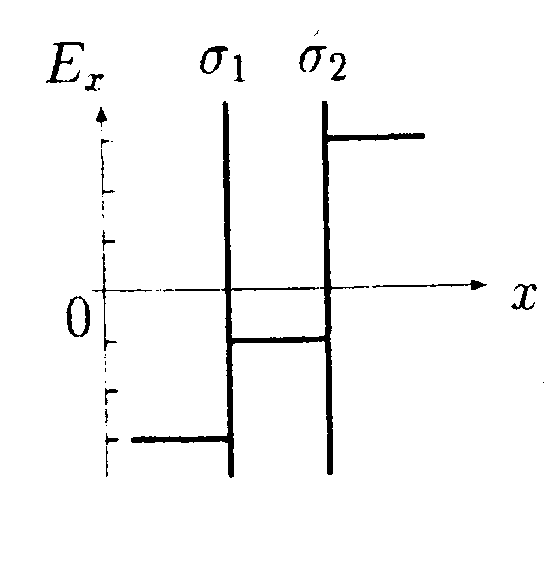 • 5.2.4. На рисунке показано распределение напряженности электростатического поля Ех(х), созданного двумя параллельными заряженными бесконечными пластинами, вдоль направления х. Как различаются поверхностные плотности зарядов σ1 и σ2 на этих пластинах по знаку и по модулю? • 5.2.5. Точечный заряд q= 1,0·10 6Кл помещен в центр куба с ребром а = 0,5 м. Чему равен поток вектора напряженности через каждую грань куба? 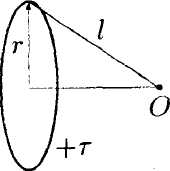 • 5.2.6. По тонкому кольцу радиусом г = 8,0 см равномерно распределен заряд с линейной плотностью τ= 10 нКл/м. Используя принцип суперпозиции, определите напряженность электростатического поля Ев точке О, равноудаленной от всех точек кольца на расстояние l = 10 см. • 5.2.6. По тонкому кольцу радиусом г = 8,0 см равномерно распределен заряд с линейной плотностью τ= 10 нКл/м. Используя принцип суперпозиции, определите напряженность электростатического поля Ев точке О, равноудаленной от всех точек кольца на расстояние l = 10 см.• 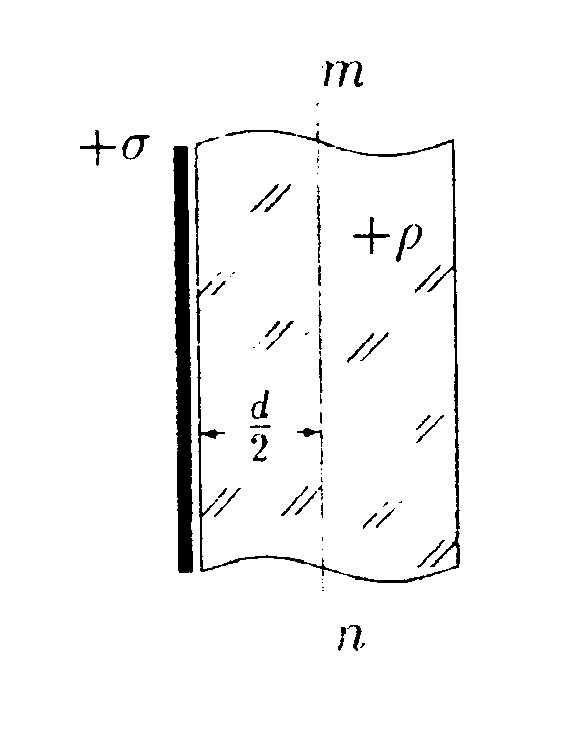 5.2.7. Бесконечная плоскость равномерно заряжена с поверхностной плотностью заряда +σ. Справа от плоскости и параллельно ей расположен бесконечно большой слой заряда толщиной d, равномерно заряженный с объемной плотностью заряда +ρ. Все заряды неподвижны. Используя теорему Гаусса и учитывая симметрию поля слоя заряда относительно плоскости mn, найдите напряженность поля Ена расстоянии d/2 от плоскости. 5.2.7. Бесконечная плоскость равномерно заряжена с поверхностной плотностью заряда +σ. Справа от плоскости и параллельно ей расположен бесконечно большой слой заряда толщиной d, равномерно заряженный с объемной плотностью заряда +ρ. Все заряды неподвижны. Используя теорему Гаусса и учитывая симметрию поля слоя заряда относительно плоскости mn, найдите напряженность поля Ена расстоянии d/2 от плоскости.5.3 Вариант 3 • 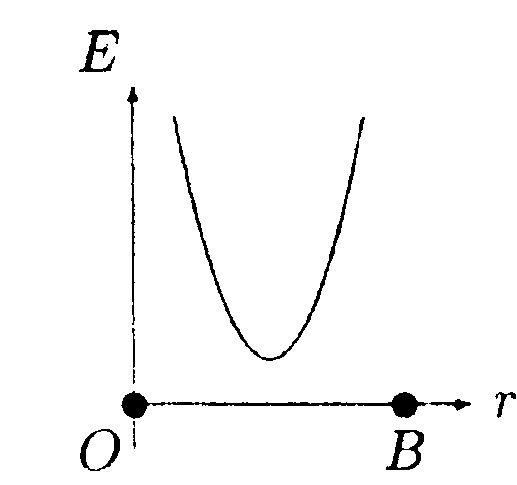 5.3.1. На некотором расстоянии друг от друга в точках О и Внаходятся два одинаковых по модулю точечных заряда. На рисунке показано распределение напряженности электростатического поля между зарядами Е(г).Определите знаки зарядов. 5.3.1. На некотором расстоянии друг от друга в точках О и Внаходятся два одинаковых по модулю точечных заряда. На рисунке показано распределение напряженности электростатического поля между зарядами Е(г).Определите знаки зарядов.• 5.3.2. Расстояние между двумя точечными зарядами q1 = 7 · 10-9Кл и q2 = -14·10-9Кл равно 5,0 см. Найдите напряженность электростатического поля в точке, находящейся на расстоянии 3.0 см от положительного заряда и 4,0 см от отрицательного. • 5.3.3. С какой силой, приходящейся на единицу площади, отталкиваются две одноименно заряженные бесконечно протяженные плоскости с одинаковой поверхностной плотностью заряда σ= - 2,0 мкКл/м2? о\ • 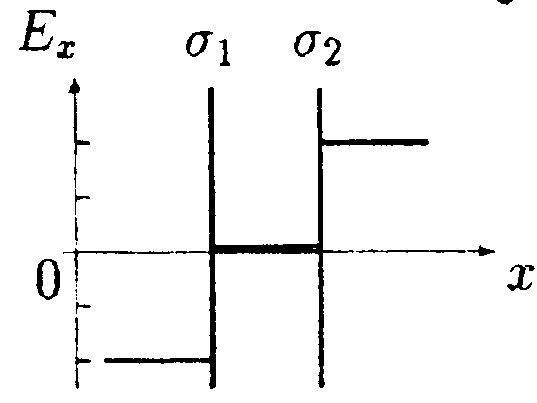 5.3.4. На рисунке показано распределение напряженности электростатического поля Ех(х), созданного двумя параллельными заряженными бесконечными пластинами, вдоль направления х. Как различаются поверхностные плотности зарядов σ1и σ2 на этих пластинах по знаку и по модулю? 5.3.4. На рисунке показано распределение напряженности электростатического поля Ех(х), созданного двумя параллельными заряженными бесконечными пластинами, вдоль направления х. Как различаются поверхностные плотности зарядов σ1и σ2 на этих пластинах по знаку и по модулю? 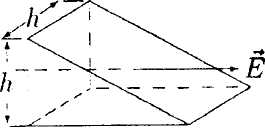 • 5.3.5. Сравните входящий и выходящий потоки вектора напряженности Е однородного электростатического поля через замкнутую поверхность прямой трехгранной призмы. Передняя грань призмы перпендикулярна Е и имеет размеры h x h, а нижняя - параллельна Е. • 5.3.5. Сравните входящий и выходящий потоки вектора напряженности Е однородного электростатического поля через замкнутую поверхность прямой трехгранной призмы. Передняя грань призмы перпендикулярна Е и имеет размеры h x h, а нижняя - параллельна Е.5.3.6. По поверхности диска радиусом R= 1,0 см равномерно распределен заряд q=1,0·10-9Кл. Используя принцип суперпозиции, найдите напряженность электростатического поля Е в точке, расположенной на перпендикуляре к диску на расстоянии h = 1.0 см от его центра. • 5.3.7. Лист стекла толщиной dс диэлектрической проницаемостью е равномерно заряжен с объемной плотностью заряда +ρ. Используя теорему Гаусса и учитывая симметрию поля слоя относительно плоскости MN, определите напряженность Е и электрическое смещение Dв точках А, В, С. Постройте графики зависимости Е(х) и D(x), где х – расстояние от точки О. 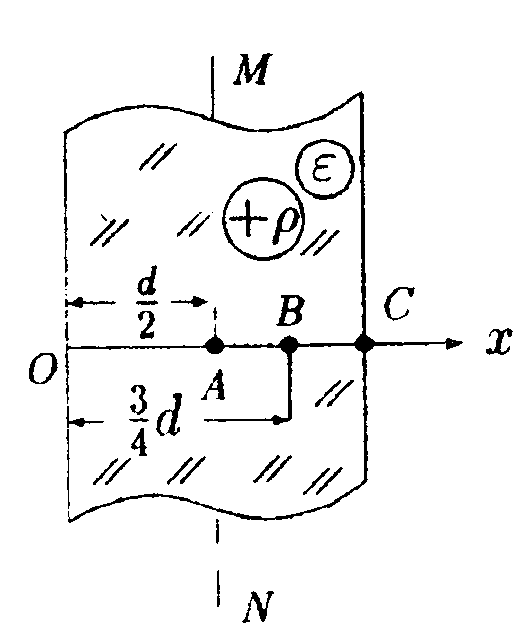 5 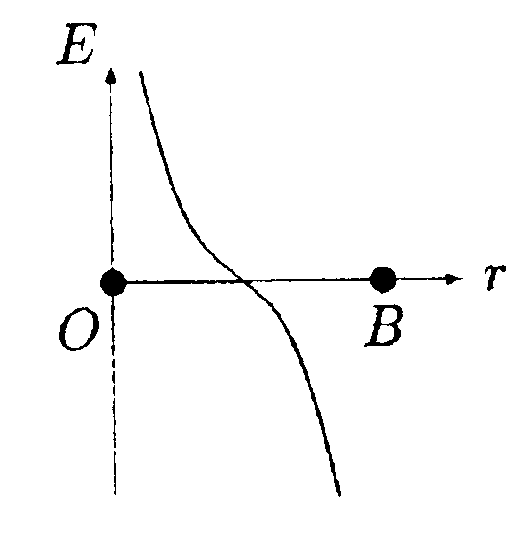 .4 . Вариант 4 .4 . Вариант 4• 5.4.1. На некотором расстоянии друг от друга в точках О к Внаходятся два одинаковых по модулю точечных заряда. На рисунке показано распределение напряженности электростатического поля Е(r) между зарядами. Определите знаки зарядов. • 5.4.2. В вершинах квадрата со стороной а находятся одинаковые заряды +q. Какой заряд Qнеобходимо поместить в центре квадрата, чтобы вся система зарядов находилась в равновесии? • 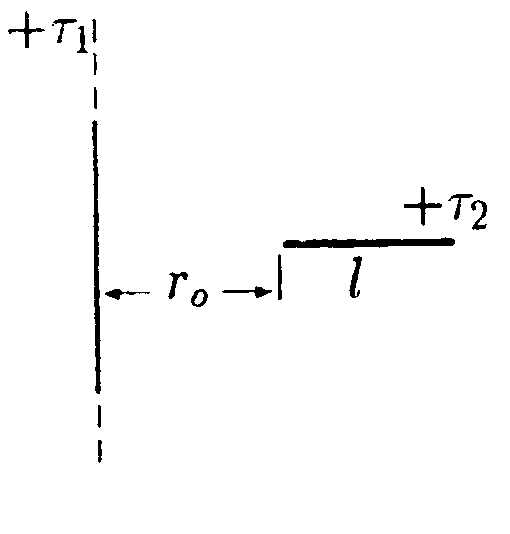 5.4.3. Бесконечная прямая нить, равномерно заряженная с линейной плотностью заряда τ1=+3,0·10-7Кл/м2, и отрезок нити длиной l = 20 см, равномерно заряженный с линейной плотностью заряда τ=+2,0·10-7Кл/м2. расположены в одной плоскости перпендикулярно друг другу на расстоянии rо = 10 см. Определите силу взаимодействия между ними. 5.4.3. Бесконечная прямая нить, равномерно заряженная с линейной плотностью заряда τ1=+3,0·10-7Кл/м2, и отрезок нити длиной l = 20 см, равномерно заряженный с линейной плотностью заряда τ=+2,0·10-7Кл/м2. расположены в одной плоскости перпендикулярно друг другу на расстоянии rо = 10 см. Определите силу взаимодействия между ними.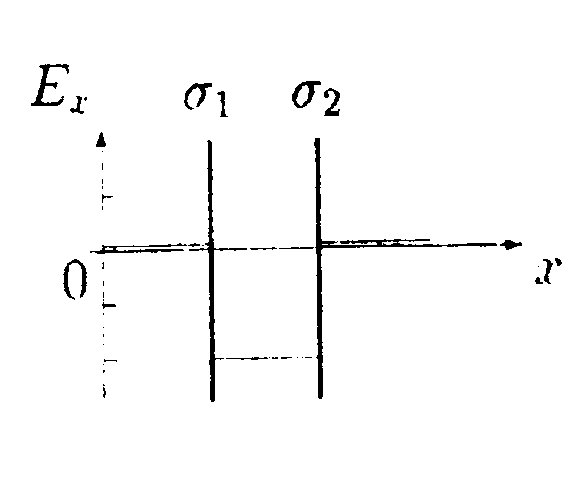 • 5.4.4 На рисунке показано распределение напряженности электростатического поля Еr(х), созданного двумя параллельными заряженными х бесконечными пластинами, вдоль направления .г. Как различаются поверхностные плотности зарядов σ1 и σ2 на этих пластинах по знаку и по модулю? • 5.4.4 На рисунке показано распределение напряженности электростатического поля Еr(х), созданного двумя параллельными заряженными х бесконечными пластинами, вдоль направления .г. Как различаются поверхностные плотности зарядов σ1 и σ2 на этих пластинах по знаку и по модулю?• 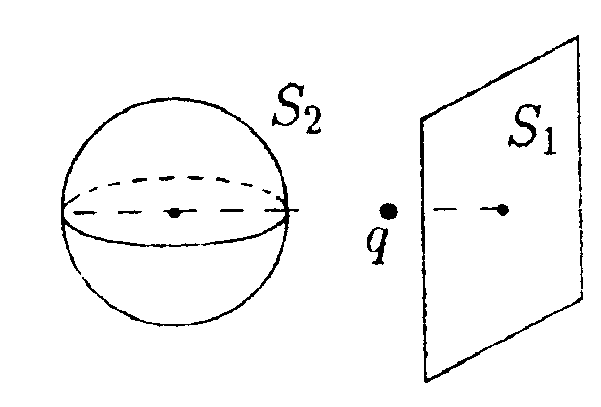 5.4.5. Вблизи точечного заряда qна равных расстояниях от него расположены, как показано на рисунке, две поверхности: плоская S1и сферическая S2Сравните потоки вектора напряженно-сти Е электростатического поля, создаваемого зарядом q, через данные поверхности. • 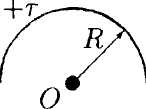 5.4.6. Тонкое полукольцо радиусом Rравномерно заряжено с линейной плотностью заряда +r. Используя принцип суперпозиции, определите напряженность электростатического поля Е в центре кривизны полукольца. • 5.4.7. По поверхности длинной металлической трубки радиусом R = 4,0-10ˉ2м равномерно распределен заряд. Напряженность электростатического поля Е на расстоянии а = 0,10 м от оси трубки равна 100 В/м. Используя теорему Гаусса, найдите линейную и поверхностную плотность заряда трубки. Постройте график зависимости Е{r), где r - расстояние от оси трубки. 5.5 . Вариант 5 • 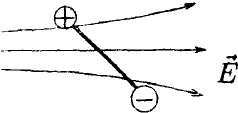 5.5.1. Что будет происходить с диполем. если его поместить в неоднородное электростатическое поле, как показано на рисунке? • 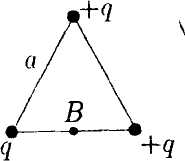 5.5.2. В вершинах равностороннего треуголь- ника со стороной а = 0,2 м помешены заряды |q|= 2,0-10ˉ9Кл. Найдите напряженность электростатического поля в точке В. расположенной на середине стороны треугольника.
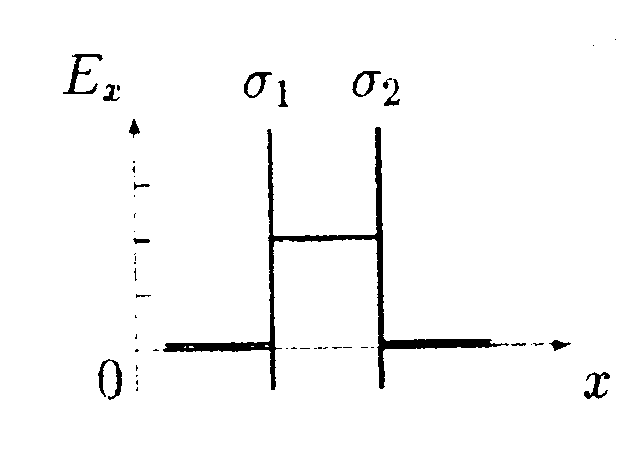 •5.5.4. На рисунке показано распределение напряженности электростатического поля Ех(х),созданного двумя параллельными заряженными бесконечными пластинами, вдоль направления х. Как различаются поверхностные плотности зарядов σ1и σ2на этих пластинах по знаку и по модулю?
|

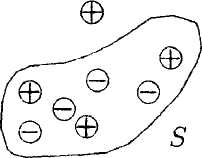
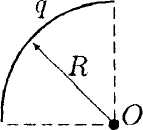 .1.6. По тонкой нити, изогнутой по дуге окружности радиусом R = 10 см, равномерно распределен заряд q = 20 нКл. Используя принцип суперпозиции, определите напряженность электростатического поля Е, создаваемого этим зарядом в центре кривизны дуги, если длина нити равна четверти длины окружности.
.1.6. По тонкой нити, изогнутой по дуге окружности радиусом R = 10 см, равномерно распределен заряд q = 20 нКл. Используя принцип суперпозиции, определите напряженность электростатического поля Е, создаваемого этим зарядом в центре кривизны дуги, если длина нити равна четверти длины окружности.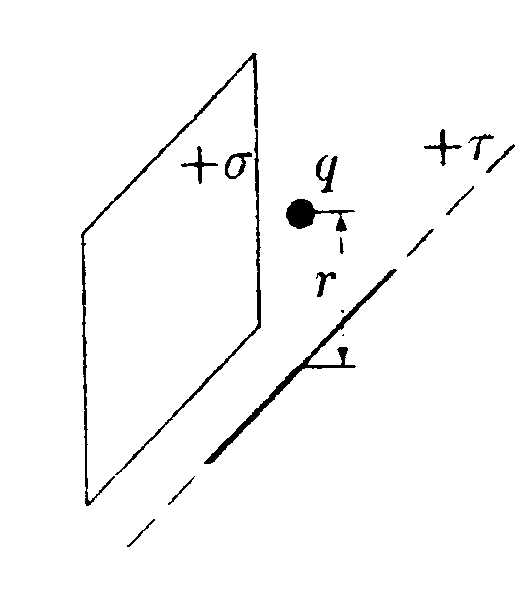
 .5.5. Прямоугольная плоская площадка со сторонами а = 3,0 см и
.5.5. Прямоугольная плоская площадка со сторонами а = 3,0 см и