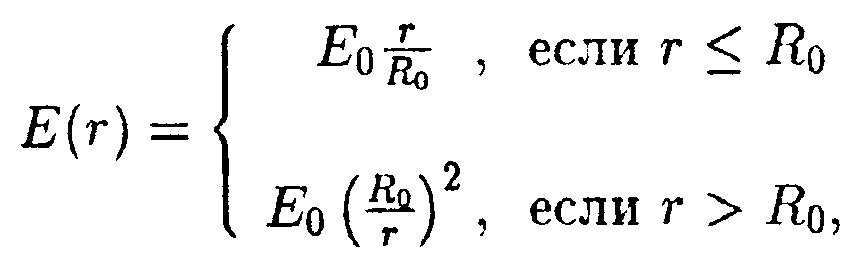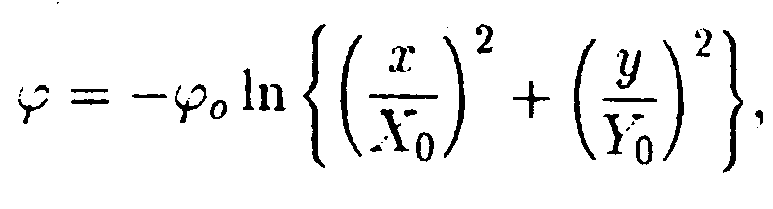|
|
Часть II Электричество и магнетизм. Сборник задач по общей физике Часть II. Электричество и электромагнетизм Под ред. Э. Б. Селивановой Библиотека Ново иб и, с ко го
6.10 . Вариант 10
·
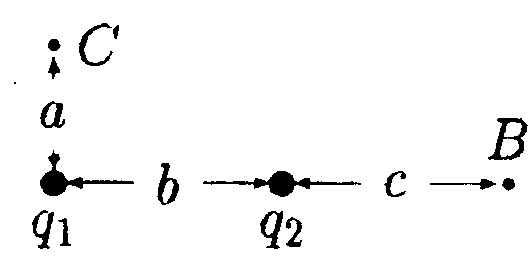
6.10.1. Определите работу электрических сил по переносу пробного заряда q = 1,0 · 10ˉ9Кл из точки С в точку B, если а = 3,0 см, b= с =4,0 см, q1 = 3,3 • 10ˉ9Кл и q2= -3,3 · 10ˉ9Кл.
6.10.2. Около заряженного по поверхности шара радиусом R = 1,0 см
находится точечный заряд q= 0,66 нКл. При перемещении заряда qиз
точки D, расположенной на расстоянии r1 = 5,0 см от центра шара,
в точку В, расположенную на расстоянии r2= 10 см от центра шара,
совершается работа А = 1,0 • 10ˉ6Дж. Найдите заряд шара Qи поверхностную плотность заряда на шаре σ.
6.10.3. Плоский конденсатор, заполненный жидким диэлектриком с диэлектрической проницаемостью ε = 3,0, зарядили, затратив на это
энергию W1 = 10 мкДж. Затем конденсатор отсоединили от источника,
слили из него диэлектрик и разрядили. Определите энергию W2. которая выделилась при разрядке.
6.10.4. Электрон, пройдя в плоском конденсаторе путь от одной пластины до другой, приобретает скорость V = 1,0 • 106м/с. Расстояние
между пластинами d = 5,3 мм. Найдите разность потенциалов Uмежду
пластинами и поверхностную плотность заряда σ на пластинах.
6
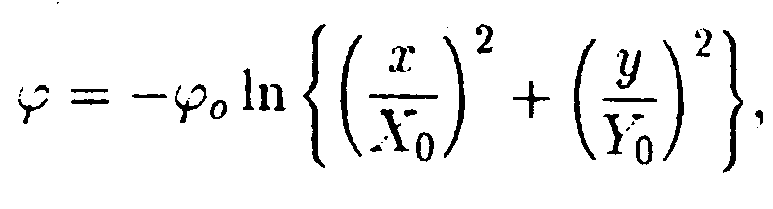
.10.5. Потенциал поля, создаваемого некоторой системой зарядов,
имеет вид
где φо = 100 В, X0 = 1,0 м, Yо =1,0 м. Изобразите примерный вид силовых и эквипотенциальных линий и найдите напряженность поля Е в точке С с координатами хс= 3,0 м, ус = 4,0 м.
6.10.6. Радиус центральной жилы каоксиального кабеля R1 =1,5 см, радиус оболочки R2= 3,5 см. Между центральной жилой и оболочкой приложена разность потенциалов U= 2,3 кВ. Найдите напряженность электрического поля Е на расстоянии r = 2,0 см от оси кабеля.
6.10.7. Найдите количество теплоты Q, которая выделяется при соединении одноименно заряженных обкладок конденсатора с емкостями С1= 2,0 мкФ и С2 = 0,5 мкФ. Разности потенциалов между обкладками конденсаторов равны соответственно U1= 100 В и U2 = 50 В.
6.11. Вариант 11
•
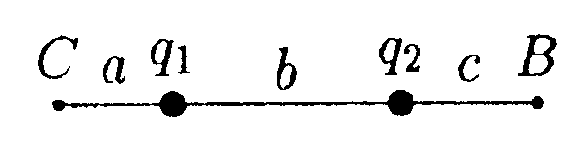
6.11.1. Определите работу электрических сил по
переносу пробного заряда q = 1,0 • 10ˉ9Кл из
точки С в точку В, если а = 3,0 см, b =10см,
с = 6,0 см, q1 = 6,6 • 10ˉ9Кл и q2= - 6,6• 10ˉ9Кл
• 6.11.2. Какая работа А совершается при перенесении точечного заряда q = 10 нКл из бесконечности в точку, находящуюся на расстоянии ∆r = 2,0 см от поверхности шара радиусом R = 5,0 см и потенциалом φ0=100B
• 6.11.3. Плоский конденсатор заполнен диэлектриком и на его пластины
подана некоторая разность потенциалов. Его энергия при этом W =70 мкДж. После того как конденсатор отключили от источника напряжения, диэлектрик вынули из конденсатора. Найдите диэлектрическую проницаемость диэлектрика ε, если работа, которая была совершена против сил электрического поля, чтобы вынуть диэлектрик. A= 20 мкДж.
• 6.11.4. Электрическое поле образовано двумя параллельными пластинами, находящимися на расстоянии d =2,0 см друг от друга. К пластинам приложена разность потенциалов U = 120 В. Какую скорость получит электрон под действием поля, пройдя вдоль линии напряженности расстояние ∆x = 3,0 мм?
• 6.11.5. Потенциал поля, создаваемого некоторой системой зарядов, имеет вид
г
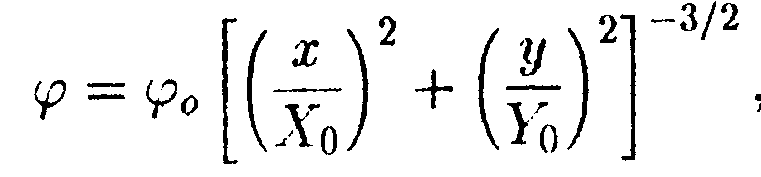
де φо = 100 В, Хо = Yо = 1,0 м. Изобразите примерный вид силовых и эквипотенциальных линий и найдите напряженность поля в точке С с координатами хс = ус =1,0 м.
6.11.6. При нормальном давлении разряд в воздухе наступает при напряженности электрического поля Е* = 3,0 МВ/м. До какого максимального потенциала φтахможно зарядить шар диаметром D= 1,0 м?
6.11.7. Точечный заряд q= 3,0 мкКл помещается в центре шарового
слоя из однородного и изотропного диэлектрика с диэлектрической проницаемостью ε = 3,0. Внутренний радиус слоя а = 2,5 см, внешний
b= 5,0 см. Найдите энергию W, заключенную в пределах диэлектрика.
6.12 . Вариант 12
•
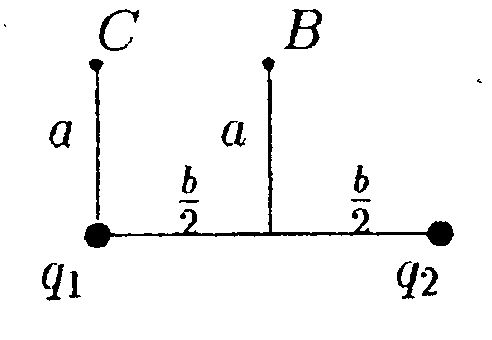
6.12.1. Определите работу электрических сил по переносу пробного заряда q= 1,0 • 10ˉ9Кл из точки С в точку В, если а = 30 см, b = 20 см, q2= 3,3 • 10ˉ9Кл и q2= 6,6 • 10ˉ9Кл.
6.12.2. На расстоянии r1= 4,0 см от бесконечно длинной заряженной
нити с линейной плотностью заряда r = 6,0 мкКл/м находится точечный заряд q = 0,33 нКл. Найдите работу электрических сил при
перемещении заряда в точку, находящуюся на расстоянии r2= 8,0 см
от нити.
6.12.3. Сферическая оболочка радиусом R1 = 5,0 см, равномерно заряженная зарядом q= 20 нКл, расширилась под действием электрических
сил до радиуса R2 = 10 см. Найдите работу электрических сил в процессе этого расширения.
6.12.4. Вакуумный цилиндрический конденсатор имеет радиус внутреннего цилиндра R1= 1,5 см и радиус внешнего цилиндраR2 = 3,5 см.
Между цилиндрами приложена, разность потенциалов U=2,3 кВ. Какую скорость Vполучит электрон под действием поля этого конденсатора, двигаясь с расстояния r1 = 2,5 см до расстояния r2= 2,0 см от оси цилиндра?
●
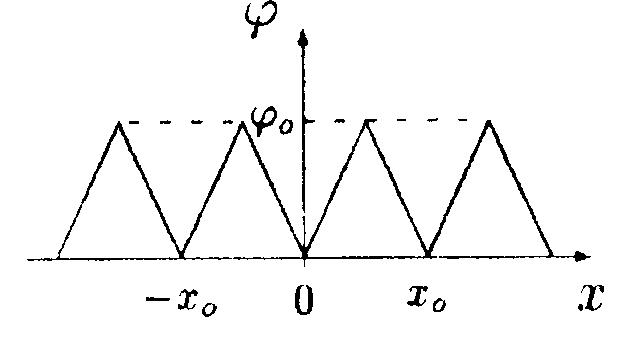
6.12.5. Зависимость потенциала электрического поля φот координаты х имеет вид, показанный на рисунке. Найдите зависимость напряженности электрического поля Е от х и изобразите ее на графике.
• 6.12.6. Тонкие стержни образуют квадрат со стороной а. На каждом
стержне равномерно распределен заряд с линейной плотностью r =1,33 нКл/м. Найдите потенциал φв центре квадрата.
• 6.12.7. Конденсатор емкостью С1= 1,0 мкФ, предварительно заряженный до напряжения U =300 В, подключили параллельно к незаряженному конденсатору емкостью С2= 2,0 мкФ. Найдите приращение
электрической энергии этой системы ∆W к моменту установления равновесия.
6.13. Вариант 13
•
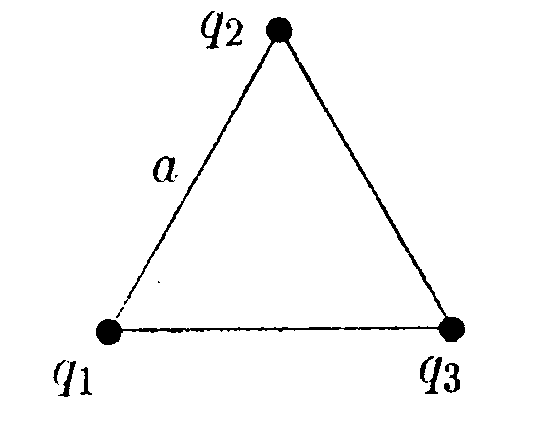
6.13.1. В вершинах равностороннего треугольника со стороной а = 4,0 см находятся заряды: q1= 1,0 • 10ˉ10Кл, q2 = 2,0 • 10ˉ10Кл, и q3 = -3,0 • 10ˉ10Кл. Какую работу нужно совершить, чтобы медленно удалить заряд q3 на бесконечность?
6.13.2. Две параллельные бесконечно длинные заряженные нити с линейной плотностью заряда r1 = 7,0 нКл/м и r2= 14,0 нКл/м находятся
на расстоянии r1 = 8,0 см друг от друга. Какую работу на единицу
длины нити необходимо затратить, чтобы раздвинуть их до расстояния r2 = 24 см?
6.13.3. Пространство между обкладками сферического конденсатора за
полнено маслом. Радиус внутренней сферической обкладки конденсатора r1= 0,5 см. а внешней r2 = 1,0 см. Напряжение на конденсаторе
U = 170 В. Найдите работу, которую нужно затратить, чтобы удалить масло из конденсатора, если конденсатор отключен от источника
питания.
6.13.4. Электрон движется вдоль силовых линий однородного электрического поля. В некоторой точке поля с потенциалом φ1= 100 В электрон имел скорость V1= 6,0 • 106 м/с. Определите потенциал φ2 точки поля, долетев до которой электрон потеряет половину своей скорости.
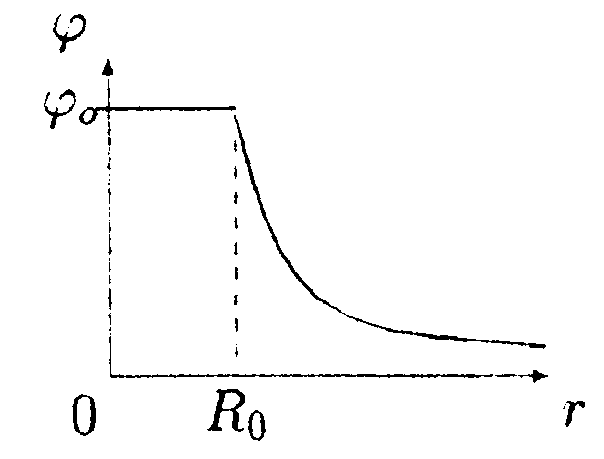
•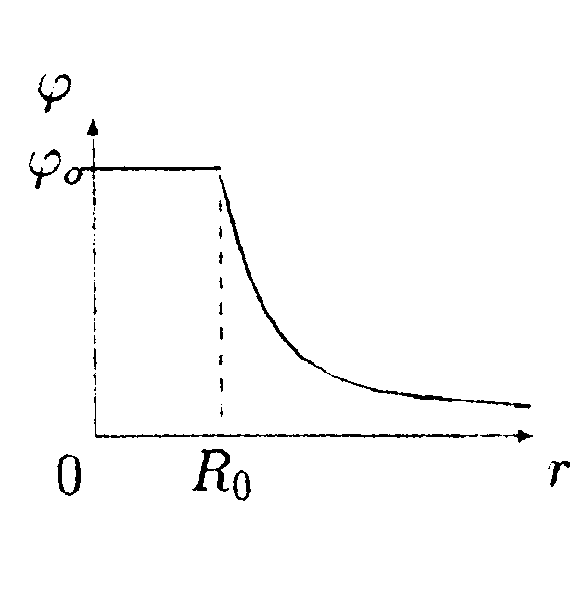 6.13.5. Зависимость потенциала электрического поля φот расстояния rимеет вид 6.13.5. Зависимость потенциала электрического поля φот расстояния rимеет вид
г
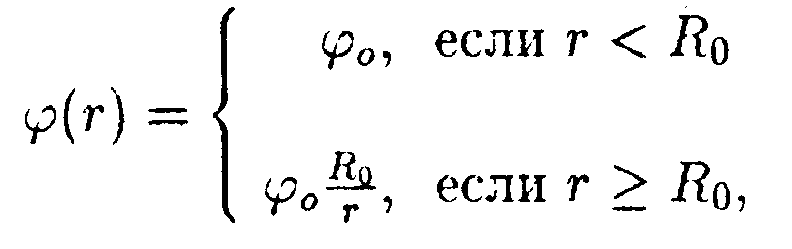
де φ0 = 100 B, Rо = 1,0 м. Найдите зависимость напряженности электрического поля Е от r, изобразите ее на графике и вычислите значение Е
при r = 3,0 м.
6.13.6. Расстояние между пластинами плоского воздушного конденсатора d = 5,0 мм, а напряжение между ними U= 6,0 кВ. Найдите как
изменится напряжение при увеличении расстояния между пластинами
конденсатора на ∆d = 3,0 мм. если источник напряжения перед раздвижением пластин отключается.
6
.13.7. Диэлектрический шар радиусом R =1,0 см равномерно заря
жен по объему зарядом Q = 0,3 мкКл. Шар находится в вакууме. Найдите энергию электрического поля, заключенную в пределах шара, и
сравните ее с полной энергией шара. Диэлектрическая проницаемость
шара ε = 2,0.
6.14 . Вариант 14
О
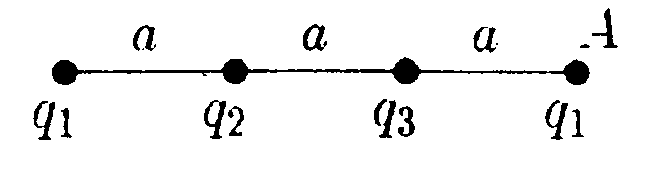
пределите работу электрических сил по переносу пробного заряда q = 1,0 • 10ˉ10Кл из точки С на бесконечность, если а = 2.0 см, q1= 2q2 =q3 = 3,0 • 10ˉ9Кл.
6.14.2. Тонкая квадратная рамка равномерно заряжена с линейной плотностью зарядаr = 200 пКл/м. Определите работу, которую необходимо затратить, чтобы удалить точечный заряд q = -3,0 нКл из точки пересечения диагоналей на бесконечность.
6.14.3. Пространство между обкладками сферического конденсатора
заполнено жидким диэлектриком с диэлектрической проницаемостью
ε = 3,0. Радиус внутренней сферической обкладки конденсатора R1 = 2,0 см, а внешнейR2 = 3,0 см. Найдите работу, которую нужно затратить, чтобы удалить диэлектрик из конденсатора, если заряд на его обкладках поддерживается постоянным и равным q = 0,5 мкКл.
6.14.4. В однородное электрическое поле напряженностью Е = 200 В/мвлетает (вдоль силовой линии) электрон со скоростью Vо= 2,0·106 м/с. Определите расстояние l, которое пройдет электрон до точки, в которой его скорость будет равна половине начальной.
•
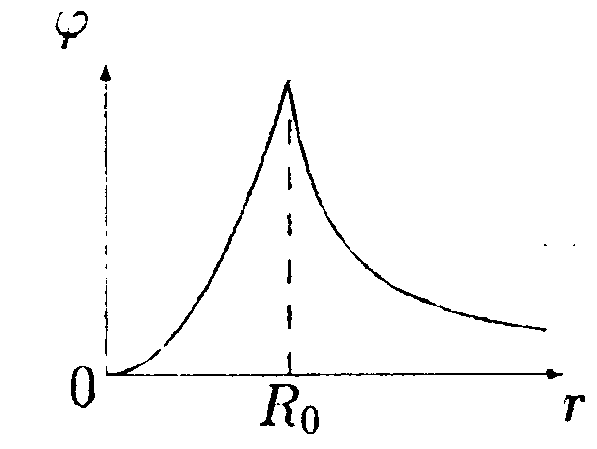
6.14.5. Зависимость потенциала электрического поля φот расстояния r имеет вид
г
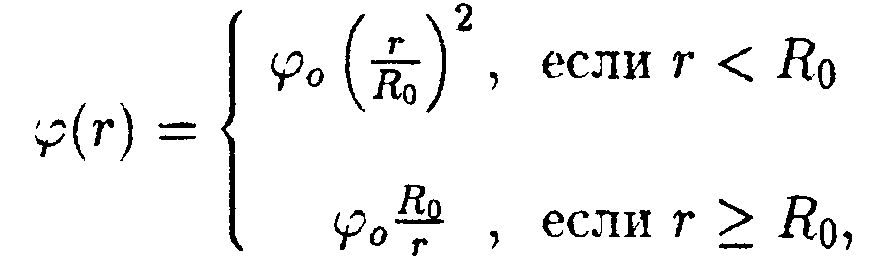
де φ0 = 1000 В, Rо = 1,0 м. Найдите зависимость напряженности электрического поля Е от г, изобразите ее на графике и вычислите значение Е при r = 0,5 м и r = 1,5 м.
6.14.6. Внутрь тонкостенной металлической сферы радиусом R= 20 см
концентрически помещен металлический шар радиусомr = 10 см.
Шар через отверстие в сфере соединен с Землей при помощи очень
тонкого длинного проводника. На внешнюю сферу помещают заряд
Q = 1,0 · 10ˉ8 Кл. Определите потенциал φэтой сферы.
6.14.7. В плоский конденсатор вдвинули пластинку парафина толщиной
d = 1,0 см, которая вплотную прилегает к пластинам конденсатора. Диэлектрическая проницаемость парафина ε = 2,0. На сколько нужно увеличить расстояние между пластинами конденсатора, чтобы получить
прежнюю емкость?
6.15 , Вариант 15
•
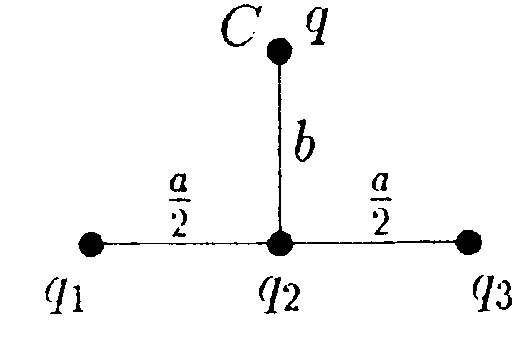
6.15.1. Определите работу электрических сил по
переносу пробного заряда q = 1,0·10ˉ9Кл из
точки С на бесконечность, если а = 4,0 см, b=
2,0 см, q1= q3 = -3,3- 10ˉ9Кл и q2 = 6,6· 10ˉ9Кл.
•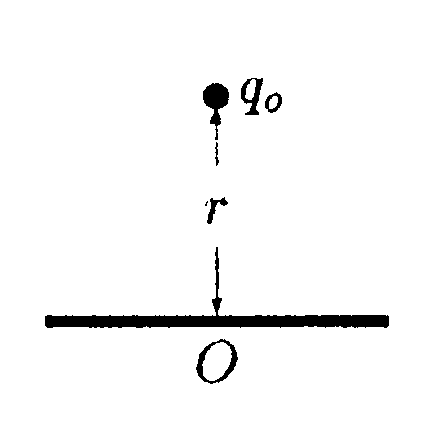 6.15.2. На тонком стержне длинойl = 20 см равномерно распределен зарядq= 0,10 мкКл. На 6.15.2. На тонком стержне длинойl = 20 см равномерно распределен зарядq= 0,10 мкКл. На
расстоянии r= 30 см от центра стержня в на
правлении перпендикулярном его оси находится
точечный заряд qо =—5,0 нКл. Найдите работу
А, которую необходимо затратить, чтобы уда
лить заряд q0на бесконечность.
6.15.3. Пространство между обкладками цилиндрического конденсатора
заполнено жидким диэлектриком с диэлектрической проницаемостью
ε= 3,0. Радиус внутренней цилиндрической обкладки конденсатора
R1 =1,0 см, а внешней R2 = 1,5 см. Длина конденсатора l= 5,0 см.
Найдите работу, которую нужно затратить, чтобы удалить диэлектрик
из конденсатора, если напряжение между обкладками поддерживается
постоянным и равным U=100 В.
6.15.4. Электрон с энергией W = 400 эВ (на бесконечности) движется
вдоль силовой линии по направлению к поверхности металлической заряженной сферы радиусом R =10 см. Определите минимальное рас
стояние а, на которое приблизится электрон к поверхности сферы, если
заряд ее q = -10 нКл.
•
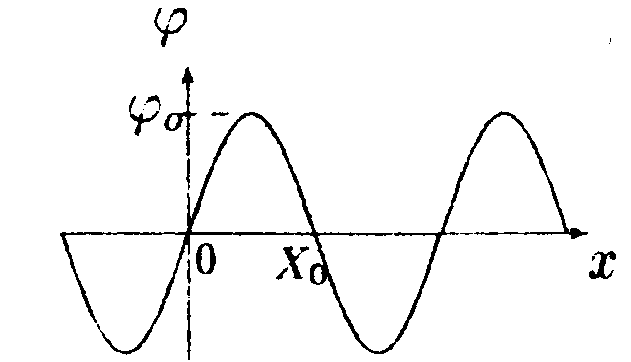
6.15.5. Зависимость потенциала электрического
поля φот координаты х определяется выражением
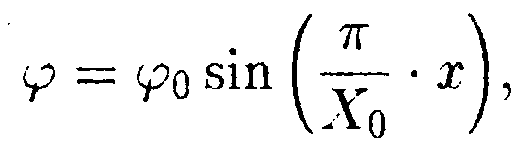
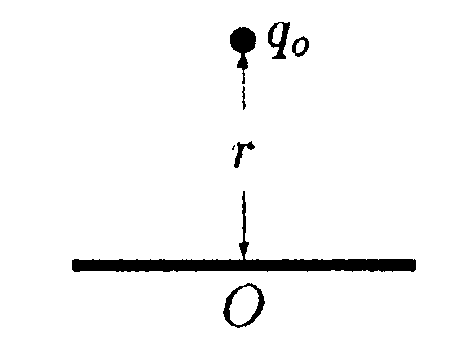
где φ0 = 1000 В, Xо = 1,0 м. Найдите зависимость напряженности электрического поля Е от x, изобразите ее на графике и вычислите значение Е при х = 0 и х = 0,5 м.
6.15.6. Две параллельные заряженные плоскости, поверхностные плотности заряда которых σ1 = 2,0 мкКл/м2 и σ2 = -0,80 мкКл/м2, находятся на расстоянии d = 0,60 см друг от друга. Определите разность потенциалов Uмежду плоскостями.
6.15.7. Два металлических шарика радиусами R1 = 5,0 см иR2= 10 см
имеют заряды Q1 = 40 нКл иQ2 = -20 нКл соответственно. Найдите
энергию W, которая выделится при разряде, если шары соединить проводником.
6.16 , Вариант 16
•
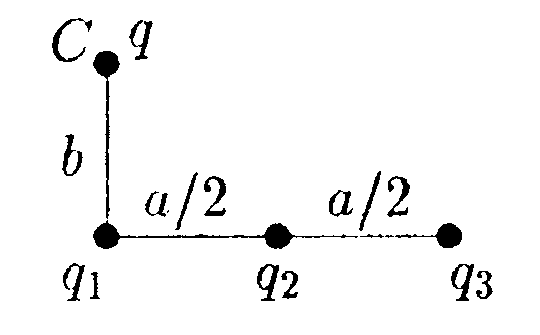
6.16.1. Определите работу электрических сил по
переносу пробного заряда q = 1,0 · 10ˉ9 Кл из
точки С на бесконечность, если а = 6,0 см, b =3,0 см, q1= q2= q3 = -3,3 • 10ˉ9 Кл.
•
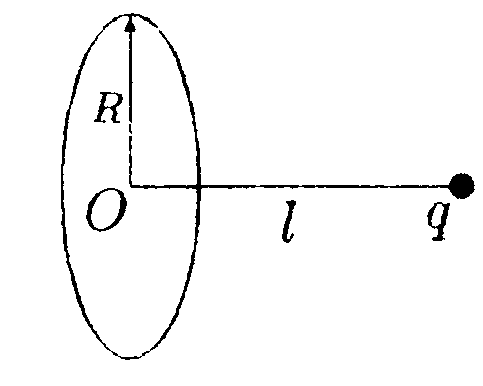
6.16.2. На тонком кольце радиусом R = 8,0 см
равномерно распределен заряд Q = 3,0 мкКл. На
оси кольца на расстоянии l = 12 см от центра О
находится точечный заряд q= -0,1 мкКл. Какую работу необходимо совершить, чтобы удалить заряд qна бесконечность?
6.16.3. Пространство между обкладками цилиндрического конденсатора
заполнено жидким диэлектриком с диэлектрической проницаемостью
ε = 2,0. Радиус внутренней цилиндрической обкладки конденсатора
R1 =2,0 см, а внешней R2 = 3,0 см. Длина конденсатораl= 10 см.
Найдите работу, которую нужно затратить, чтобы удалить диэлектрик
из конденсатора, если он отключен от источника напряжения, а заряд
на его обкладках q=10 нКл.
6.16.4. Определите ускоряющую разность потенциалов U, которую должен пройти электрон в электрическом поле, чтобы его скорость возросла в два раза. Начальная скорость электронаVо = 1,0 · 106 м/с.
•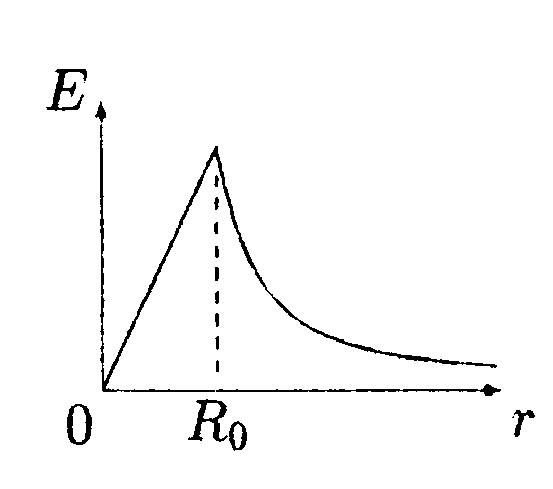 6.16.5. Зависимость напряженности сферически- симметричного электрического ноля Е от рас- стояния задана выражением 6.16.5. Зависимость напряженности сферически- симметричного электрического ноля Е от рас- стояния задана выражением
г
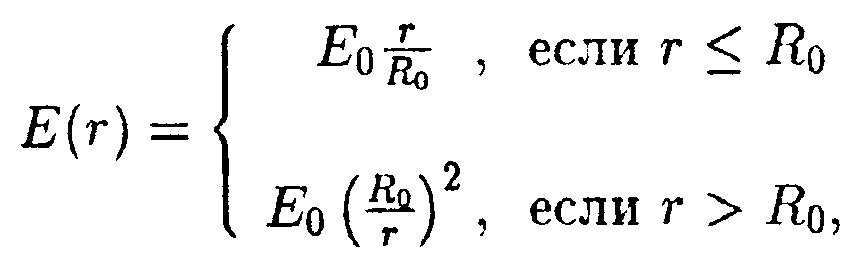
де Ео=1000 В/м, Rо = 1,0 м. Найдите зависимость потенциала электрического поля φот r, изобразите ее на графике и вычислите значение φпри r = 0,5 м. Значение потенциала на бесконечности положить равным нулю.
6.16.6. Внутри полой тонкостенной сферы радиусом Rнаходится сфера
радиусомr. Сфере радиусом Rсообщается заряд Q, а сфере радиусом
r - заряд q. Определите потенциалы сфер.
6.16.7. На плоский воздушный конденсатор с толщиной воздушного слоя
d = 1,2 см подается напряжение U=32 кВ. Будет ли пробит конденсатор, если предельная напряженность электрического поля в воздухе
Е* = 30 кВ/см?
|
|
|
 Скачать 40.78 Mb.
Скачать 40.78 Mb.



 6.13.5. Зависимость потенциала электрического поля φот расстояния rимеет вид
6.13.5. Зависимость потенциала электрического поля φот расстояния rимеет вид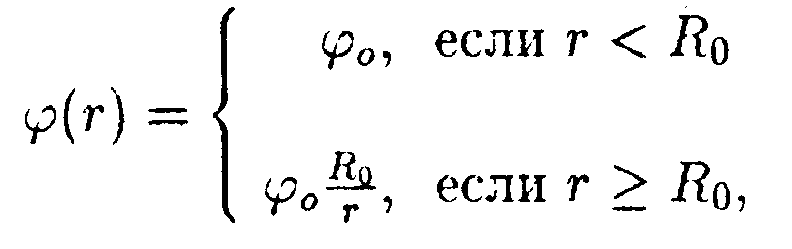


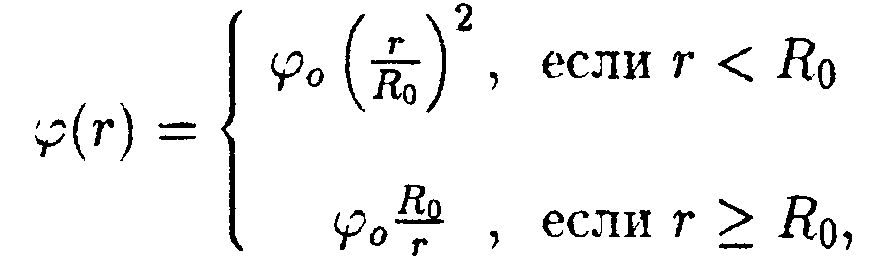
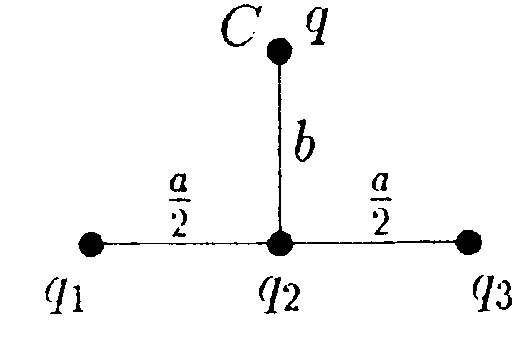
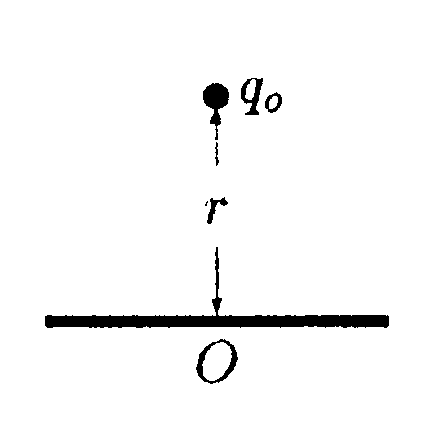 6.15.2. На тонком стержне длинойl = 20 см равномерно распределен зарядq= 0,10 мкКл. На
6.15.2. На тонком стержне длинойl = 20 см равномерно распределен зарядq= 0,10 мкКл. На
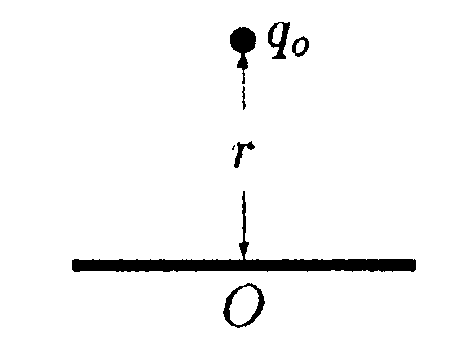

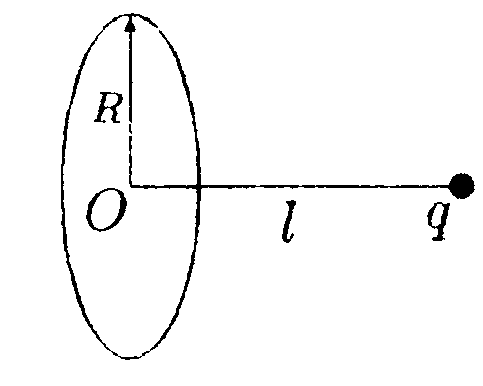
 6.16.5. Зависимость напряженности сферически- симметричного электрического ноля Е от рас- стояния задана выражением
6.16.5. Зависимость напряженности сферически- симметричного электрического ноля Е от рас- стояния задана выражением