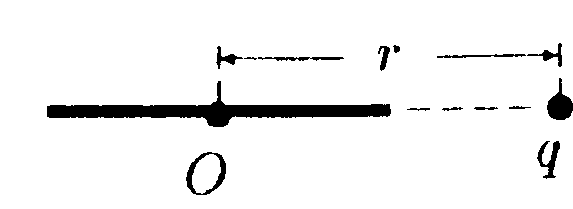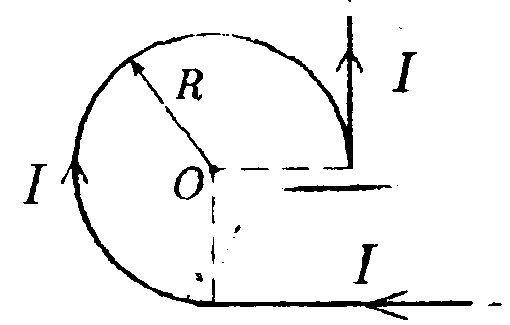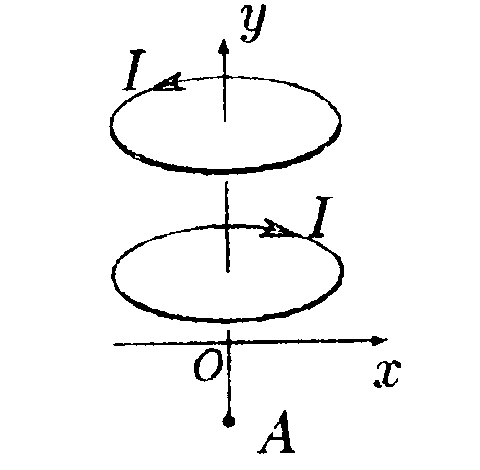Часть II Электричество и магнетизм. Сборник задач по общей физике Часть II. Электричество и электромагнетизм Под ред. Э. Б. Селивановой Библиотека Ново иб и, с ко го

• Название: Сборник задач по общей физике Часть II. Электричество и электромагнетизм Под ред. Э. Б. Селивановой Библиотека Ново иб и, с ко го
• Анкор: Часть II Электричество и магнетизм.doc
• Дата: 24.12.2017
• Размер: 40.78 Mb.
• Имя файла: Часть II Электричество и магнетизм.doc
• Тип: Сборник задач; #12775
• страница: 6 из 9

6.17. Вариант 17

• 
  6
  
  
  
  .17.1. В плоскости ху в точке О с координатами
  х₀= 0, у₀ =0 находится заряд q₀ =3,0 • 10ˉ⁹Кл,
  а в точке В с координатами хв = 2,0 см, ув=
  0 заряд qв = -2,0 • 10ˉ⁹Кл. Какую работу
  нужно совершить, чтобы перенести пробный за
  ряд д = 1,0 • 10ˉ⁹Кл из точки С с координатами
  х_с= 1,0 см. yс = 1,0 см в точку D с координатами хD= 3,0 см, уD = 2,0 см?
  
• 
  6
  
  .17.2. На тонком стержне длинойl = 10 см равномерно распределен заряд Q = 5,0 нКл. На оси
  стержня на расстоянии r= 30 см от его центра
  находится точечный заряд q = -0,5 нКл. Найдите работу, которую необходимо затратить,
  чтобы удалить заряд qна бесконечность.
  

• 
  6
  
  .17.3. В центре сферической оболочки, на поверхности которой равно­
  мерно распределен заряд Q= 5,0 мкКл, расположен точечный заряд
  q = 1,5 мкКл. Найдите работу электрических сил при расширении обо­лочки - увеличении ее радиуса от R1 = 50 мм до R₂ = 100 мм.
  
• 
  6.17.4. Три электрона в состоянии покоя помещены в вершинах правильного треугольника со стороной а = 3,0 см. Они начинают двигаться
  под действием сил взаимного отталкивания. Определите предельную
  скорость каждого электрона.
  

•

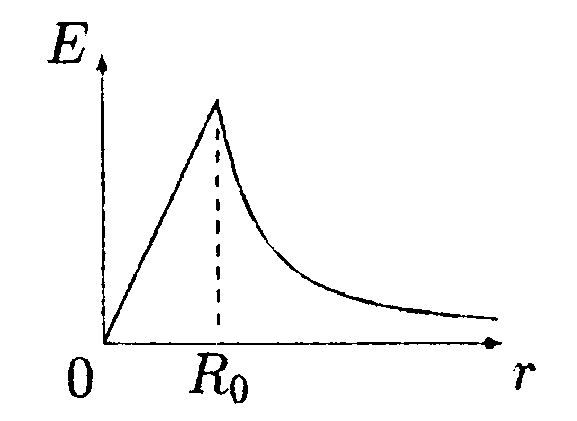
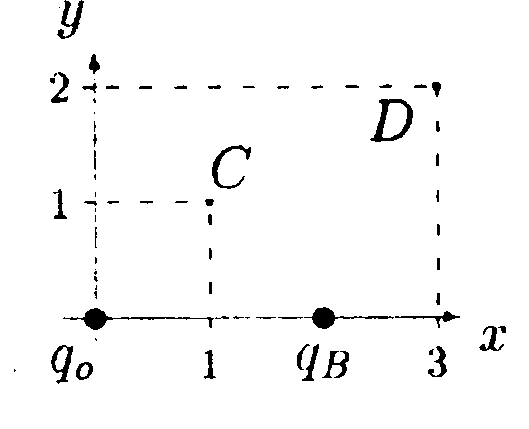
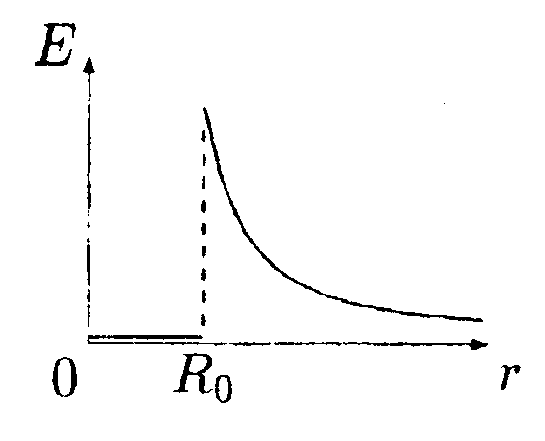
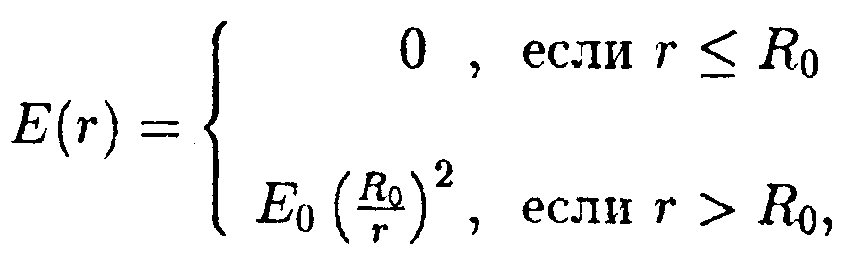6.17.5. Зависимость напряженности сферически-симметричного электрического поля Е задана выражением

где Ео = 100 В/м, Rо = 0,1 м. Найдите зависи­мость потенциала электрического поля φ от r, изобразите ее на графике и вычислите значение φпри r= 0,2 м. Значение потенциала на беско­нечности положить равным нулю.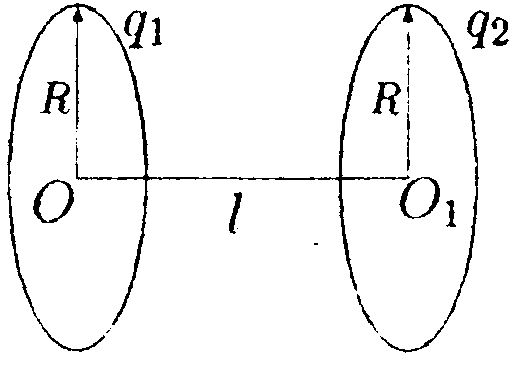

•

6.17.6. Имеются два заряженных тонких прово­лочных кольца радиусом R= 30 см каждое. Плоскости колец параллельны, а их центры ле­жат на одной оси на расстоянии l = 52 см. Заряды колец равны q1 = 0,4 мкКл и q2 = -0,4 мкКл. Найдите разность потенциалов φ между центрами колец.

• 6.17.7. Площадь пластин плоского воздушного конденсатора S = 12,5 см², а расстояние между ними d1 = 5,0 мм. Найдите изменение емкости конденсатора ∆С и энергии ∆W электрического поля при уве­личении расстояния между пластинами до d2= 10 мм, если источник напряжения перед этим был отключен.

6.18 . Вариант 18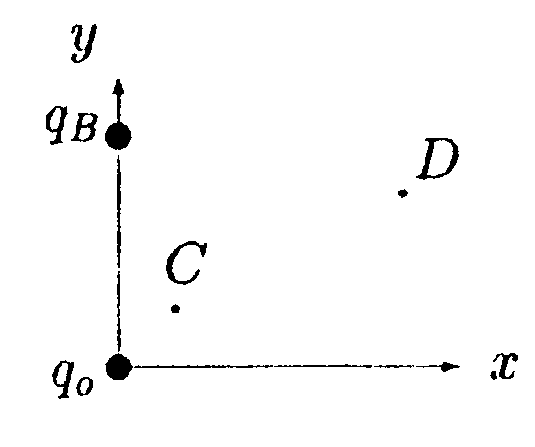

•

6.18.1. В плоскости ху в точке О с координатами
x₀ = 0, у₀ =0 находится зарядq₀= 6,0 • 10ˉ⁹Кл,
а в точке В с координатами хв = 0, ув= 4,0 см
заряд qв = -3,0 • 10ˉ⁹Кл. Какую работу нужно
совершить, чтобы перенести пробный заряд q=
1,0 • 10ˉ⁹Кл из точки С с координатами хс =
1,0 см, yс = 1,0 см в точку Dс координатами
хD= 3,0 см, уD= 2,0 см?

• 
  6.18.2. На расстоянии r1 = 1,0 см от центра равномерно заряженного
  по поверхности бесконечно длинного цилиндра с поверхностной плотностью заряда σ = 10 мкКл/м² находится точечный заряд q = 2,0 нКл.
  Под действием сил электрического поля заряд q перемещается в точку,
  находящуюся на расстоянии r2 =2,0 см от оси цилиндра. При этом
  совершается работа А = 8,0 • 10ˉ⁶Дж. Найдите радиус цилиндра R.
  
• 
  6.18.3. Две концентрические сферические оболочки с радиусами R1=
  3,0 см и R2 = 5,0 см равномерно заряжены с поверхностными плотностями зарядов σ1= -0,1 мкКл/м² и σ₂ = 0,1 мкКл/м². Найдите работу
  электрических сил при расширении внешней оболочки (увеличении ее
  радиуса) на величину ∆R=1,0 см. Диэлектрическая проницаемость
  среды ε = 1,5.
  
• 
  6.18.4. Пылинка массой т= 5,0 нг, имеющая заряд 10 электронов, про­шла в вакууме ускоряющую разность потенциалов U= 1,0 МВ. Найдите приращение скорости пылинки.
  

•

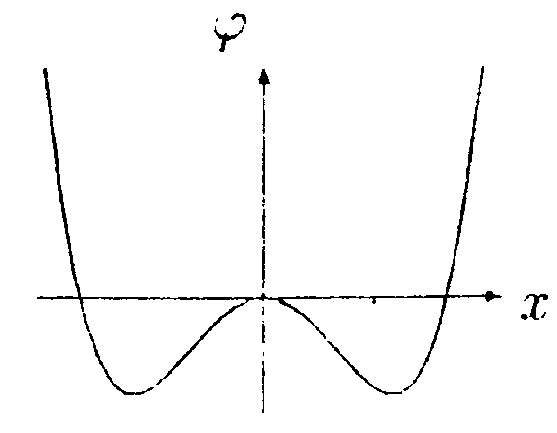6.18.5. Зависимость потенциала электрического
поля φот координаты x задана выражением

г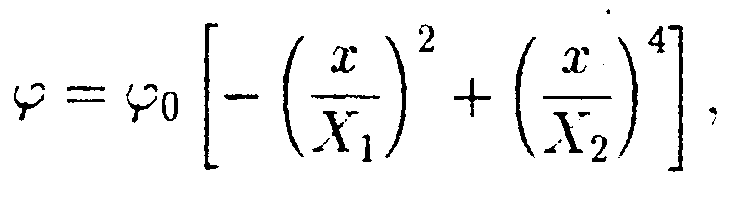

де X1 = 2,0 м, X2 = 4,0 м. Найдите зависимость напряженности электрического поля Е от x, изобразите ее на графике и вычислите значение Е при х = √2 м и х= -√2 м.
• 6.18.6. Металлический заряженный шарик помещен в центре толстого
сферического слоя, изготовленного: а) из металла; б) из диэлектрика с
диэлектрической проницаемостью ε = 2,0.

1. 
   Нарисуйте картины силовых линий внутри и вне сферического слоя.
   
2. 
   Изобразите графически зависимости напряженности поля и потенциала от расстояния, поместив начало координат в центре сферы.
   

• 6.18.7. Во сколько раз отличается объемная плотность энергии электри­ческого поля в точке, находящейся на расстоянии х = 2,0 см от поверх­ности заряженного шара радиусом R = 1,0 см, от объемной плотности
энергии бесконечной плоскости? Поверхностная плотность зарядов на
шаре и плоскости равны между собой.

7 . Тема: Магнитное поле в вакууме 7.1. Вариант 1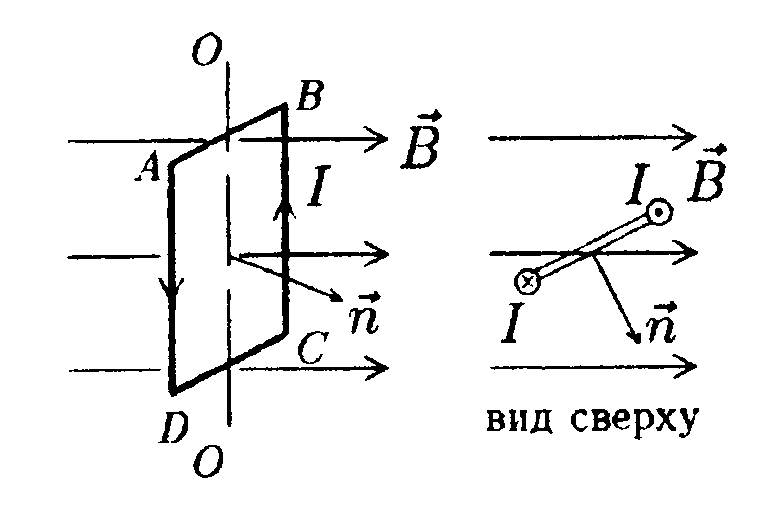

•

7.1.1. На рисунке показана прямоугольная рамка (контур) с током в однородном магнитном поле. Укажите направление: а) векторов сил Ампера, действующих на все стороны рамки; б) вектора вращающего момента рамки относительно оси ОО.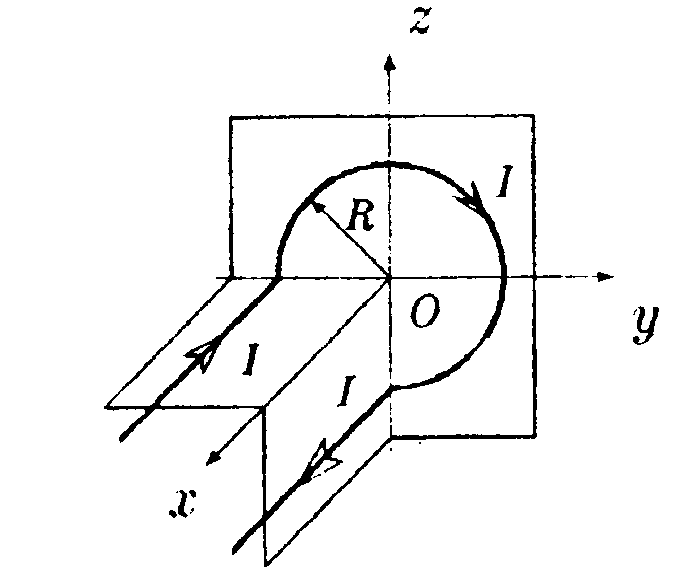

•

7.1.2. Найдите индукцию магнитного поля в точке О, если проводник с то ком I имеет вид, показанный на рисунке. Прямолинейные участки проводника очень длинные.

• 
  7.1.3. По трем параллельным прямым проводам, находящимся на одинаковом расстоянии d= 20 см друг от друга, текут токи одинаковой силы I= 400 А. В двух проводах направление токов совпадает. Вычислите силу, действующую на единицу длины каждого провода.
  
• 
  7.1.4. По проводу, согнутому в виде квадрата со стороной a = 10 см,
  течет ток I= 100 А. Найдите магнитную индукцию В в точке пересечения диагоналей квадрата.
  
• 
  7.1.5. По внутреннему проводнику диаметром 1,0 мм коаксиального кабеля течет ток 5,0 А, а по внешнему, диаметром 10 мм, течет ток в
  

обратном направлении 10 А. Найдите индукцию магнитного поля В в точках на расстояниях R1 = 3,0 мм, R2 = 10 мм.

7.1.6. Равномерно заряженный диск вращается с угловой скоростью ω = 100 сˉ¹. Радиус дискаR= 0,1 м, поверхностная плотность заряда σ = 10 Кл/м². Найдите индукцию магнитного поля на оси диска в точке, на расстоянии х от центра диска.

7.2 _: Вариант 2

1. 
   Укажите направление вектора индукции
   магнитного поля dB, созданного в точке А эле-
   ментом тока Idl,если точка и элемент тока рас
   положены в плоскости х0у.
   
2. 
   Б
   
   
   
   есконечно длинный тонкий проводник с
   током Iимеет изгиб (плоскую петлю) радиусом
   R. Определите индукцию магнитного поля, создаваемого током в точке О.
   

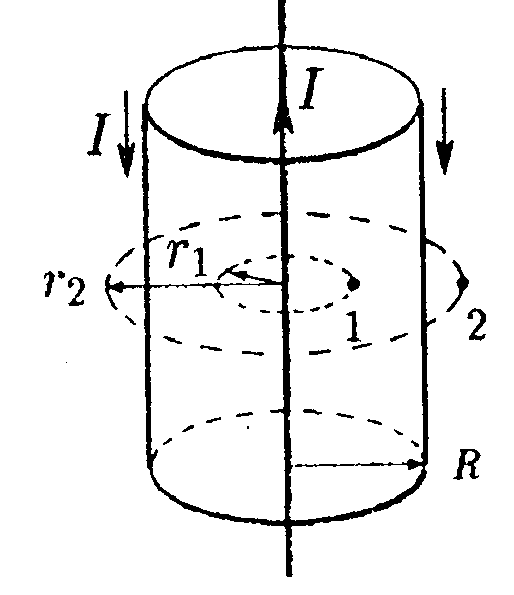
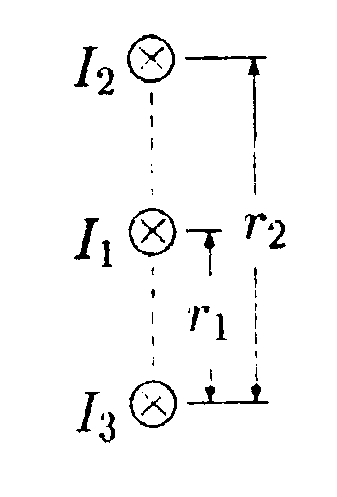7.2.3. По двум длинным параллельным проводникам

текут токи I1 = 12= 2000 А в одном направлении.

В одной плоскости с проводниками параллельно им

закреплен отрезок прямого проводника длиной l = 0,5 м с током Iз. Определите Iз, если после снятия

закрепления он начинает двигаться с ускорением а = 1 м/с². Масса проводника т = 0,1кг. он расположен

на расстоянииr1 = 0,20 м от одного и r₂= 0,40 м от

другого проводника.

7.2.4. По проводнику, согнутому в виде окружности, течет ток. Индукция магнитного поля в центре окружности равна 251,2 Тл. Не изменяя силы тока в проводнике, ему придали форму квадрата. Определите индукцию магнитного поля в точке пересечения диагоналей этого квадрата.

• 7.2.5. Коаксиальный кабель представляет собой длинную металлическую тонкостенную трубку радиусом R= 10 мм, вдоль оси которой рас­положен тонкий провод. Силы токов в трубке и проводе равны, направления противоположны. Определите магнитную индукцию в точках 1 и 2, удаленных соответственно на расстояния r1 = 5,0 мм и r2= 15 мм от оси кабеля, если сила тока I= 0,5 А.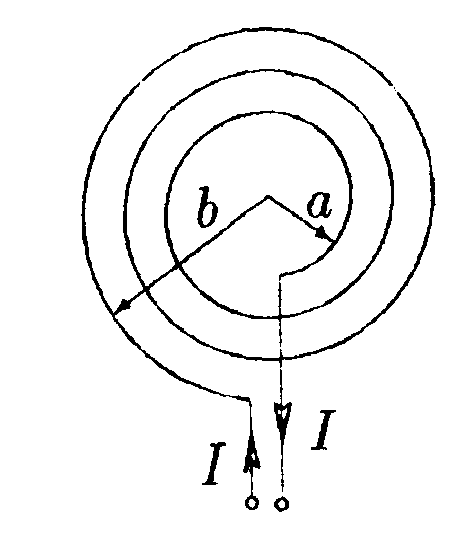

•

7.2.6. Тонкий провод (с изоляцией) образует пло­скую спираль из большого числа N плотно рас­положенных витков, по которым течет посто­янный ток I. Радиусы внутреннего и внешнего витков равны а иb. Найдите магнитную индук­цию В в центре спирали.

7.3 . Вариант 3

• 
  7
  
  .3.1. Поле создано двумя круговыми токами,
  равными по величине. Осью симметрии круговых токов является ось у. Определите направле­ние вектора индукции в точке А.
  
• 
  7
  
  
  
  .3.2. Возле бесконечного прямолинейного про­
  водника 1 с током Iрасположен подвижный, пря­молинейный конечной длины проводник CDтак,
  что он лежит в плоскости, проходящей через про­
  водник 1 и перпендикулярен ему. Что будет про­
  исходить с проводником CD, если по нему пропу­стить ток Iв направлении, указанном стрелкой?
  

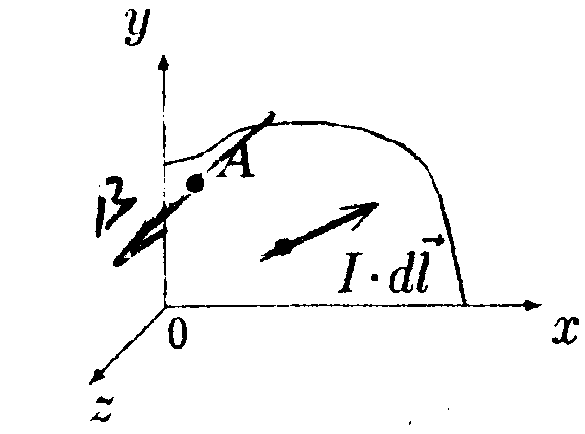
• 7.3.3. Квадратная проволочная рамка расположена в одной плоскости с длинным прямым проводом так, что две ее стороны параллельны про­воду. По рамке и проводу текут одинаковые токи I = 1000 А. Опреде­лите силу, действующую на рамку, если ближайшая к проводу сторона рамки находится на расстоянии, равном ее длине.

• 7.3.4. К тонкому однородному проволочному кольцу радиусом Rподводят ток I = 2,0 А в направлении, указанном стрелками. Найдите индукцию магнитного поля в центре кольца, если подводящие провода, делящие кольцо на две дуги l1и l2, расположены радиально и имеют бес­конечную длину.

7.3.5. По соленоиду длиной l= 1,0 м без сердечника, имеющему N =10³ витков, течет ток I= 20 А. Определите циркуляцию вектора магнитной индукции вдоль контура, изображенного на рисунке а) и б).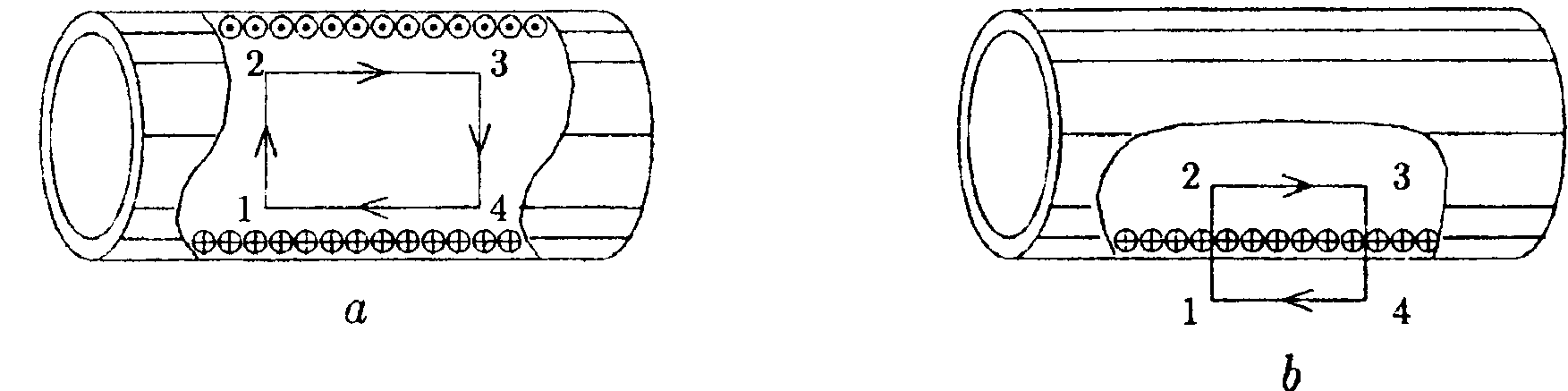

•

7.3.6. Под длинной горизонтальной шиной на двух одинаковых пружи­нах с жесткостью k= 5,0 • 10ˉ³ Н/м подвешен прямой горизонталь­ный провод длиной 80 см, который может перемещаться в вертикальной плоскости. Расстояние от провода до шины в отсутствие токов равно 30 см. Найдите расстояние между шиной и проводом, если по шине идет ток I1 = 12 А, а по проводу I2 = 5,0 А и если токи антипараллельны.

7.4 . Вариант 4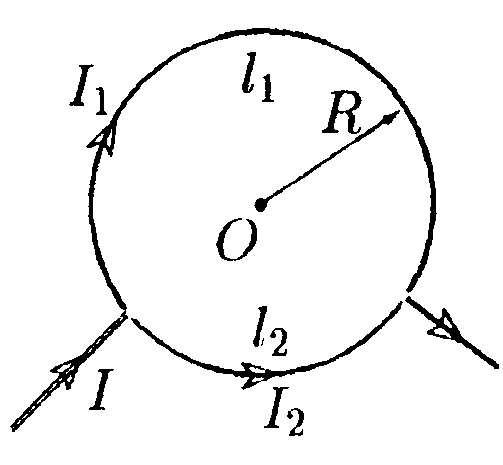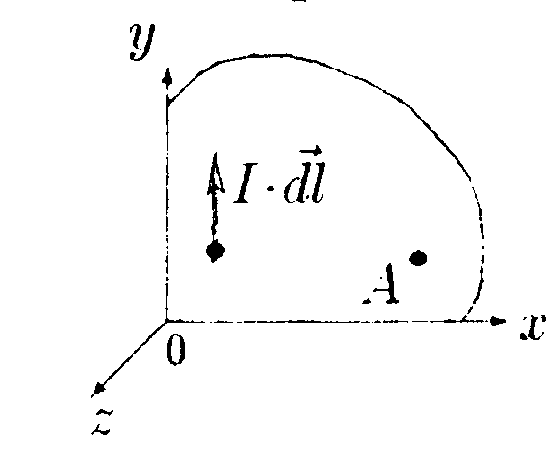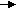

•



7.4.1. Укажите направление вектора индукции магнитного поля dB, созданного в точке А элементом тока Idl, если точка А и элемент тока I·dlрасположены в плоскости хОу.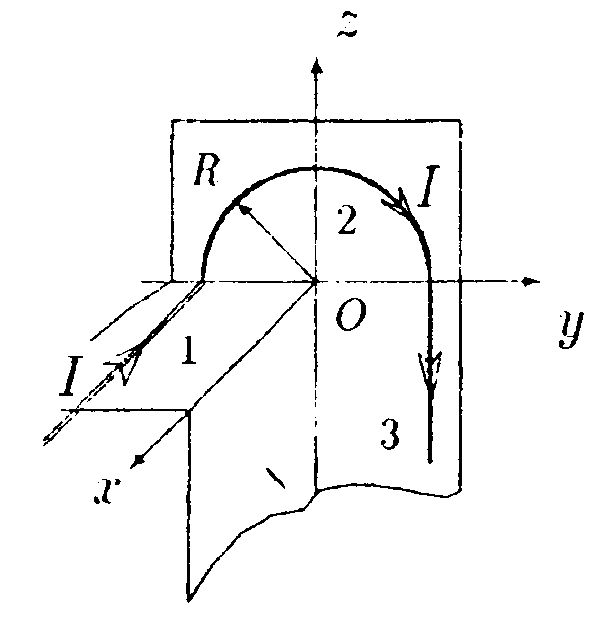

•

7.4.2. Найдите индукцию магнитного поля в точке О. если проводник с током I имеет вид, показанный на рисунке. Прямолинейные участки проводника очень длинные.

• 7.4.3. По длинному прямому проводнику М и параллельному ему от
резку проводника К длиной 60 см текут противоположно направлен
ные токи I= 100 А. Проводник К закреплен на расстоянииr1 = 10 см
от проводника М. После открепления проводника К он переместился
поступательно до r₂ = 100 см от проводника М. Определите работу
перемещения проводника К.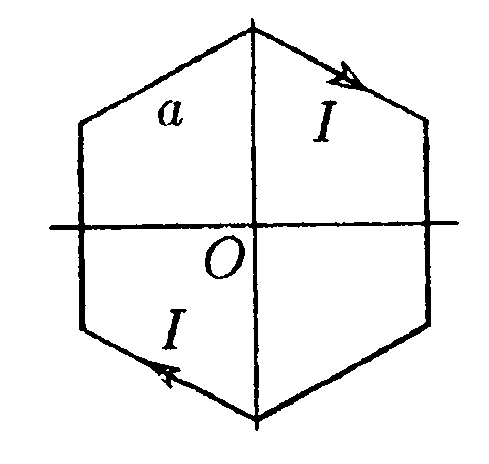

•

7.4.4. По тонкому проводнику, изогнутому в виде правильного шестиугольника со стороной а = 10 см, идет ток I = 20 А. Определите магнитную индукцию в центре шестиугольника.

• 
  7.4.5. По бесконечно длинному прямому проводу радиусом rтечет ток I.
  Ток распределен равномерно по сечению провода. Найдите индукцию
  магнитного поля внутри и вне провода, используя закон полного тока.
  
• 
  7.4.6. Тонкий диск, радиусом R= 25 см, сделан из диэлектрика и
  равномерно заряжен по поверхности. Заряд диска Q= 5,0 Кл. Диск
  вращается в воздухе вокруг оси, проходящей через его центр и перпендикулярной его плоскости, с постоянной угловой скоростью, делая v=5 оборотов за секунду. Определите магнитную индукцию в центре диска.
  

7.5 . Вариант 5

• 
  7
  
  .5.1. Четыре прямых бесконечных проводника
  с токомI. расположены на одинаковом расстоянии а друг от друга. Найдите направление век
  тора индукции магнитного поля, созданного токами, в точке О.
  
• 
  7
  
  .5.2. Бесконечно длинный тонкий проводник с
  током I имеет изгиб (плоскую петлю) радиусом R. Определите индукцию магнитного поля,
  созданного током в точке О.
  

7.5.3. Проводник в виде тонкого полукольца радиусом R =10 см находится в однородном магнитном поле с индукцией В = 50 мТл. По проводнику течет ток I = 10 А. Найдите силу F, действующую на про­водник, если плоскость полукольца перпендикулярна линиям индукции.

• 7.5.4. По контуру в виде равностороннего треугольника течет ток I=50 А. Сторона треугольника а = 20 см. Определите магнитную индукцию В в центре треугольника.

• 7.5.5. Определите циркуляцию вектора магнитной индукции вдоль контуров а, b, с, изображенных на рисунке, если в обоих проводах текут токи 8,0 А.

• 7.5.6. По двум одинаковым квадратным плоским контурам со стороной
а = 20 см текут токи I= 10 А в каждом. Определите силу Fвзаимодействия контуров, если расстояние dмежду соответствующими сторонами контуров равно 2,0 мм.

7.6 . Вариант 6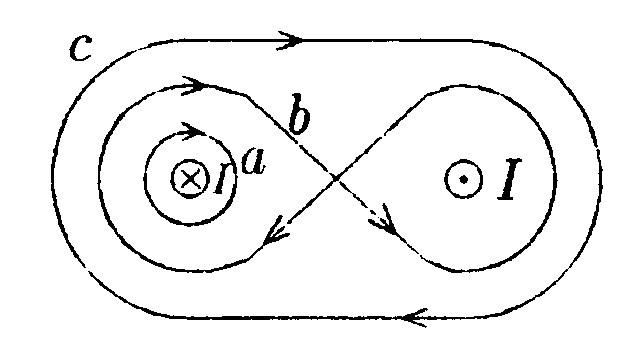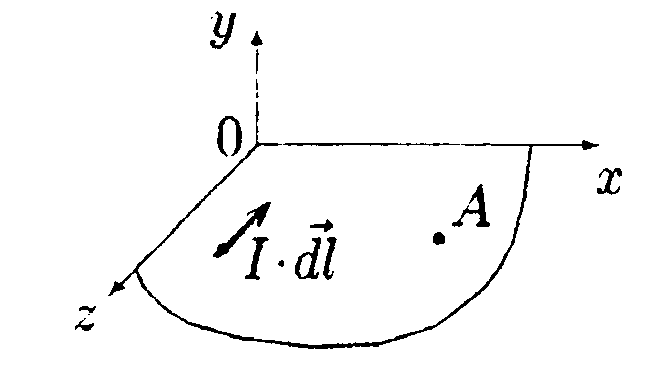

•



7.6.1. Укажите направление вектора индукции магнитного поля dB, созданного в точке А элементом тока I-dl, если точка А и элемент тока расположены в плоскости xOz.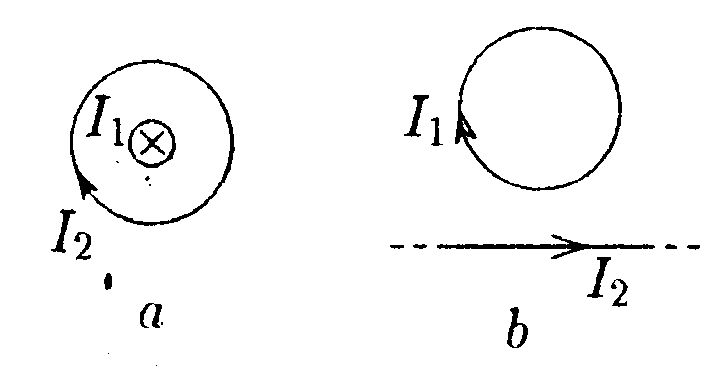

•

7.6.2. В каком случае изображенные на рисунке проводники с током
не взаимодействуют друг с другом?
Ответ обосновать.

• 7.6.3. По прямому горизонтально расположенному проводу проходит ток I₁ = 5.0 А. Под ним находится второй, параллельный ему алюминиевый провод, по которому пропускают ток I2= 1,0 А. Расстояние между про водами d = 1.0 см. Какова должна быть площадь поперечного сечения второго провода, чтобы он находился в состоянии равновесия незакрепленным?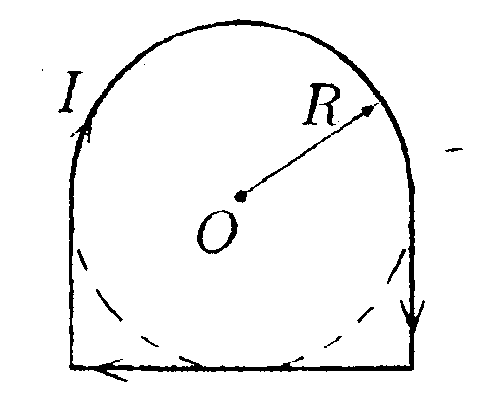

•

7.6.4. По плоскому контуру из тонкого провода течет ток I = 100 А. Определите магнитную индукцию В поля, создаваемого этим током в точке О. Радиус изогнутой части контура равен 20 см.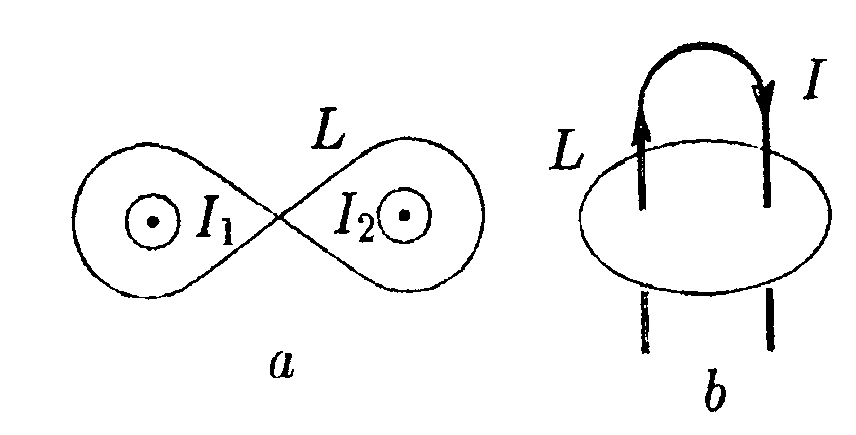

•

7.6.5. Определите циркуляцию век­тора магнитной индукции В по кон­туру Lдля конфигурации токов, при­веденных на рисунке. 11 = I = 10 А, I₂ = 5 А.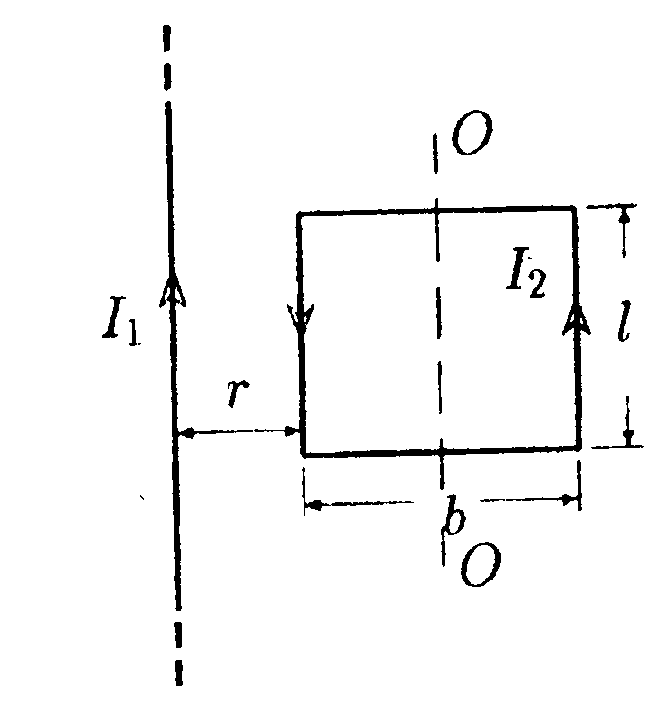

•

7.6.6. Прямой бесконечный ток 11 = 5,0 А и пря­моугольная рамка с током 12= 3,0 А располо­жены в одной плоскости так, что сторона рамки l= 1,0 м параллельна прямому току и отстоит от него на расстоянии r = 0,1b. где b- длина другой стороны рамки. Определите какую работу необ­ходимо совершить для того, чтобы повернуть рамку на угол а = 90° относительно оси ОО, параллельной прямому току и проходящей через середины противоположных сторон рамки b.