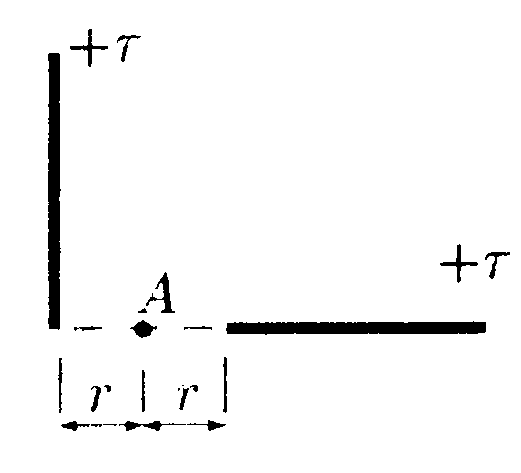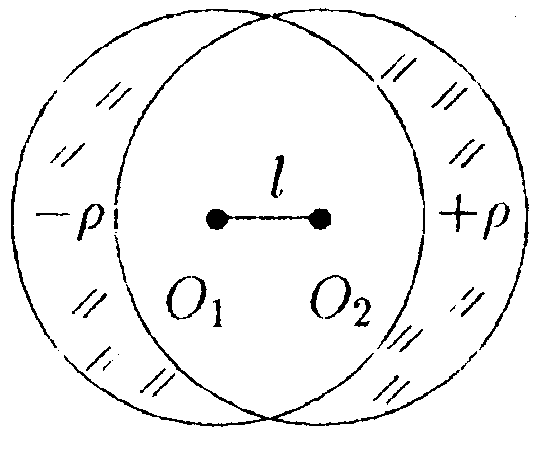Часть II Электричество и магнетизм. Сборник задач по общей физике Часть II. Электричество и электромагнетизм Под ред. Э. Б. Селивановой Библиотека Ново иб и, с ко го

• Название: Сборник задач по общей физике Часть II. Электричество и электромагнетизм Под ред. Э. Б. Селивановой Библиотека Ново иб и, с ко го
• Анкор: Часть II Электричество и магнетизм.doc
• Дата: 24.12.2017
• Размер: 40.78 Mb.
• Имя файла: Часть II Электричество и магнетизм.doc
• Тип: Сборник задач; #12775
• страница: 3 из 9

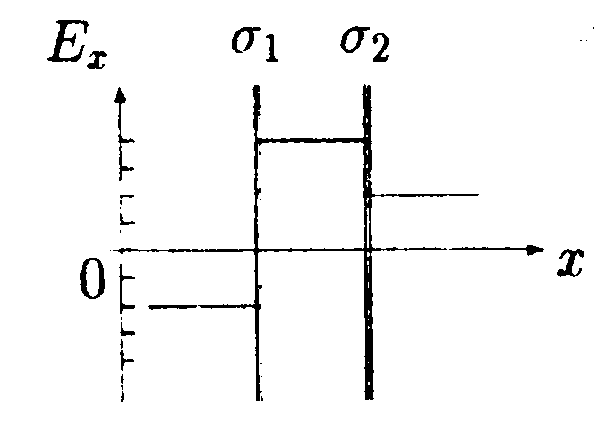
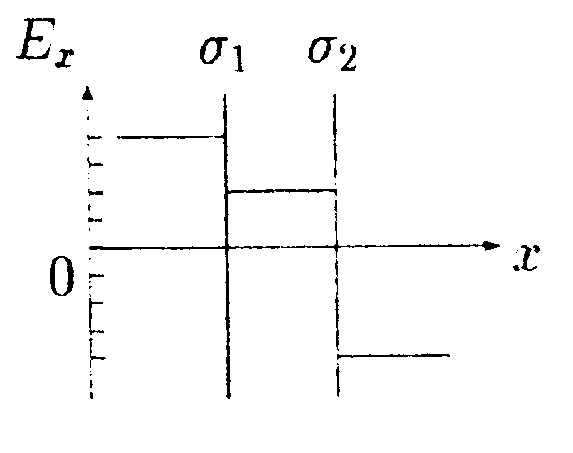
5.13. Вариант 13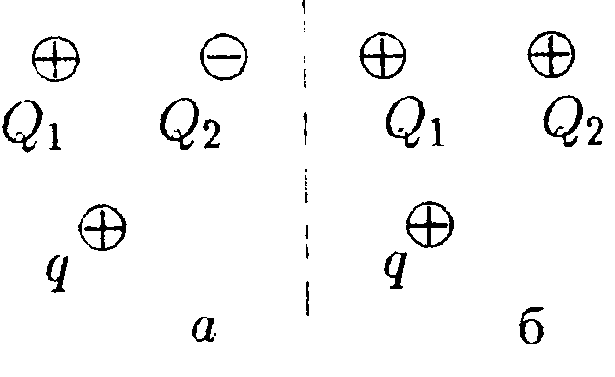

•

5.13.1. В поле, созданном двумя точечными зарядами Q1 и Q2, может свободно переме­шаться пробный заряд q. Укажите напра­вление движения пробного заряда в случаях а и б, изображенных на рисунке.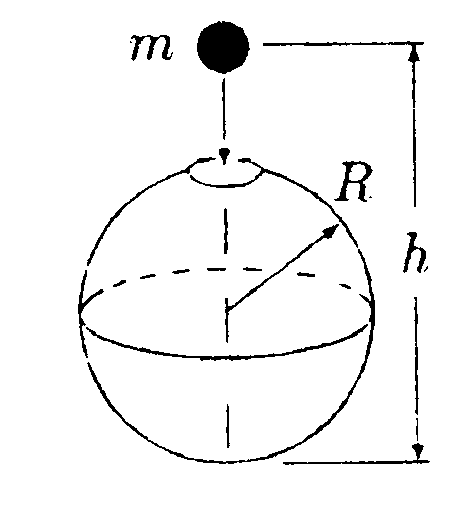

•

5.13.2. В сферический металлический сосуд ра­диусом R, в верхней части которого имеется не­большое отверстие, с высоты hпадают заряжен­ные капельки ртути. Масса каждой капли m, за­ряд Q. Каким будет номер п последней капли, которая еще может попасть в сосуд? Сопроти­влением воздуха и напряженностью поля Земли пренебрегите.
• 5.13.3. Точечный заряд q = 25 нКл находится в поле, созданном прямым бесконечным цилиндром радиусом R = 1,0 см, равномерно заряженным с поверхностной плотностью заряда σ =+0,20 нКл/см². Определите силу, действующую на заряд, если заряд находится на расстоянии r= -10 см от оси цилиндра.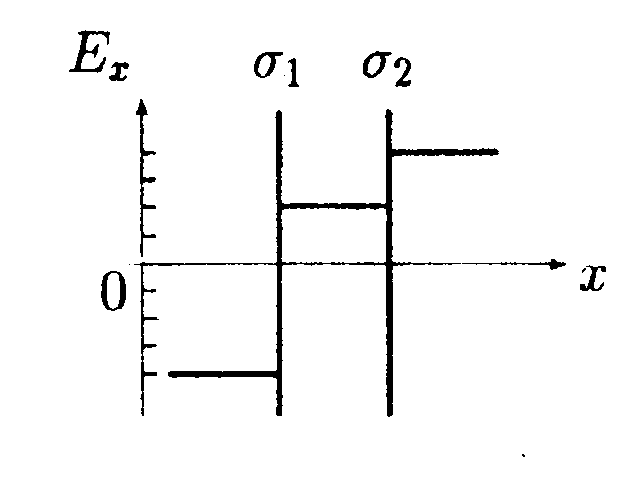



• 5.13.4. На рисунке показано распределение на­пряженности электростатического поля Е_х(х), созданного двумя параллельными заряженными бесконечными пластинами, вдоль направления х. Как различаются поверхностные плотности за­рядов σ1и σ2 на этих пластинах по знаку и по модулю?

• 
  5.13.5. Точечный заряд находится в центре сферической поверхности.
  Изменится ли поток вектора напряженности электростатического поля,
  если сферу заменить кубом того же объема?
  
• 
  5.13.6. На тонком полукольце радиусом R = 20 см равномерно рас­
  пределен заряд Q₁ = 2,0 • 10ˉ⁶Кл. Используя принцип суперпозиции,
  определите силу, действующую на точечный заряд Q₂= 4,0·10ˉ⁸Кл,
  расположенный в центре кривизны полукольца.
  
• 
  5.13.7. Стеклянный шаровой слой равномерно заряжен по объему с объ­емной плотностью заряда +р. Внутренний радиус шарового слоя R1,
  наружный — R₂. Используя теорему Гаусса, найдите зависимость на-пряженности Е и электрического смешения Dот расстояния г, от­
  считываемого от центра шара. Постройте графики зависимости Е(r)
  и D(r). Диэлектрическая проницаемость стекла равна ε .
  

5.14 • Вариант 14

• 
  5
  
  .14.1. Возможно ли существование такого электростатического поля, вектор напряженности
  которого во всех точках вдоль оси х имеет одинаковое направление, а его модуль изменяется по линейному закону?
  
• 
  5
  
  .14.2. Два одинаковых заряженных шарика
  массой т подвешены в одной точке на нитях
  длиной l каждая. В точке подвеса находится третий шарик, заряженный так же, как и первые
  два. Вычислите заряд шариков, если угол между
  нитями в положении равновесия равен α.
  

• 5.14.3. Металлический шар имеет заряд q1 = 0,20 мкКл. Вдоль силовой
линии поля, создаваемого шаром, расположена равномерно заряженная
нить так, что ближний конец ее удален от поверхности шара на расстояние, равное радиусу шара. По нити распределен заряд q2 = 5,0 нКл.
Длина нити равна радиусу шара. Определите силу, действующую на
нить, если радиус шара R= 20 см.

• 5.14.4. На рисунке показано распределение напряженности электростатического поля Е_х(х),
созданного двумя параллельными заряженными
бесконечными пластинами, вдоль направления х.
Как различаются поверхностные плотности за­
рядов σ1и σ2 на этих пластинах по знаку и по
модулю?

• 
  5.14.5. Поверхностная плотность заряда на бесконечной равномерно за­
  ряженной плоскости равна 3,0 • 10ˉ¹⁰Кл/м². Вычислите поток вектора
  напряженности электростатического поля Е через поверхность сферы
  диаметром 1,0 м, рассекаемой этой плоскостью пополам.
  
• 
  5.14.6. Тонкий стержень длиной l = 0,5 м равномерно заряжен с линей­
  ной плотностью заряда т = 1,0·10ˉ⁶Кл/м. Используя принцип суперпозиции, найдите напряженность электростатического поля в точке,
  находящейся на расстоянии а = 0.1 м от стержня и равноудаленной
  от его концов. Как изменится напряженность поля, если: 1) а << l;
  2) а >> l?
  

•



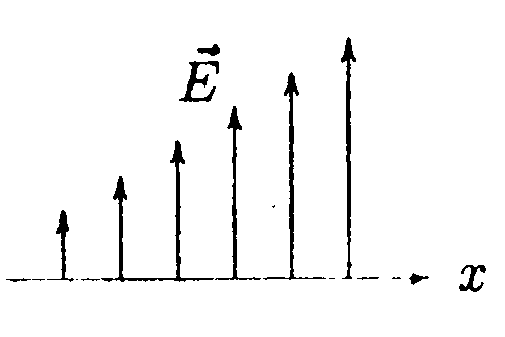
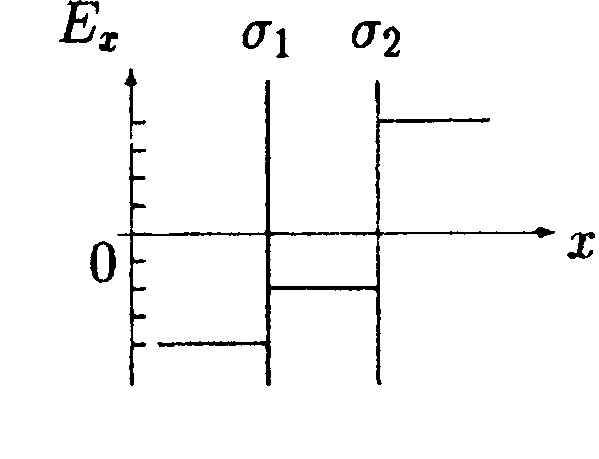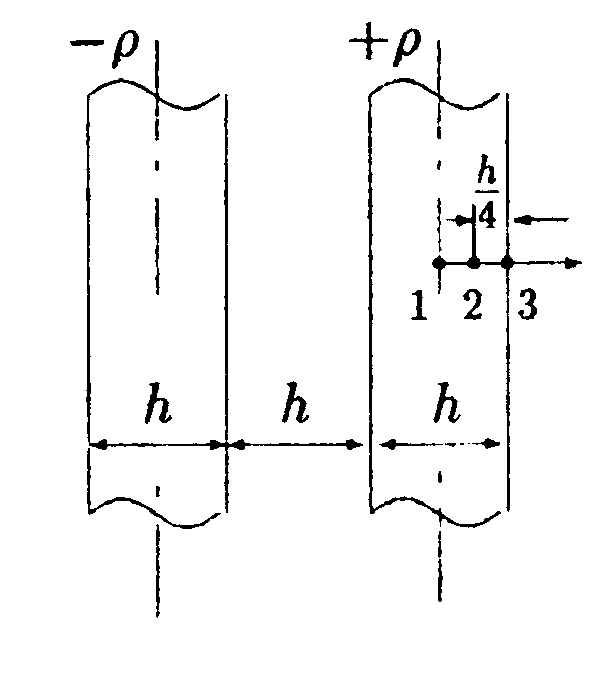5.14.7. Расстояние между разноименно заряженными пластинами и толщина пластин равны h.Объемная плотность заряда пластин равна р. Используя теорему Гаусса и учитывая симметрию поля каждой пластины относительно ее центральной плоскости, найдите напряженность электростатического поля в точках 1, 2, 3.
5.15 . Вариант 15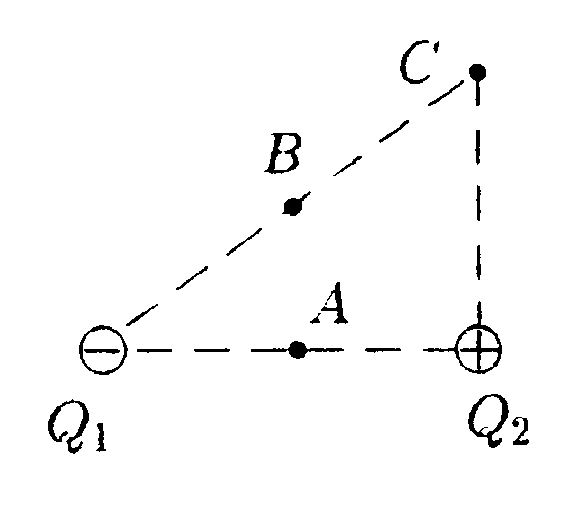

•

5.15.1. Поле создается равными по модулю за­
рядами |Q1| = |Q2|, расположенными в углах
прямоугольного треугольника. Укажите напра­вления векторов напряженности электростати­ческого поля в точках А, В, С (точки А и В
лежат на середине сторон треугольника). Срав­ните модули результирующих векторов напря­женности в указанных точках.

• 5.15.2. Два одинаковых положительных точечных заряда q₁ = q₂ = q
находятся на расстоянии 2l =10 см друг от друга. Найдите на прямой,
являющейся осью симметрии этих зарядов, точку, в которой напряженность электростатического поля будет максимальной.

• 
  5
  
  .15.3. На рисунке показаны поперечные сече­ния тонких бесконечных равномерно заряженных
  стержней, параллельных друг другу. Линейная
  плотность заряда на стержнях одинакова и равна
  |r| = 2,0 ·10ˉ⁹Кл/м. Определите силу взаимодействия между стержнями на единицу длины. Рас­стояние между стержнями а = 2,0 м.
  
• 
  5
  
  .15.4. На рисунке показано распределение напряженности электростатического поля Е_х(х),
  созданного двумя параллельными заряженными
  бесконечными пластинами, вдоль направления х.
  Как различаются поверхностные плотности за­рядов σ1и σ 2 на этих пластинах по знаку и по модулю?
  
• 
  5
  
  .15.5. Полусфера радиусом Rнаходится в од­нородном электростатическом поле, напряженность которого равна Е. Определите поток век­тора напряженности ФEчерез полусферу.
  

• 5.15.6. На оси заряженного проволочного кольца симметрично относи­тельно его центра расположены два точечных заряда q. Если заряды поместить в точках, отстоящих от центра кольца на расстояниях, равных его радиусу, то система оказывается в равновесии. Чему равен заряд кольца? Будет ли равновесие устойчивым? Для расчета напря­женности электростатического поля кольца используйте принцип су­перпозиции.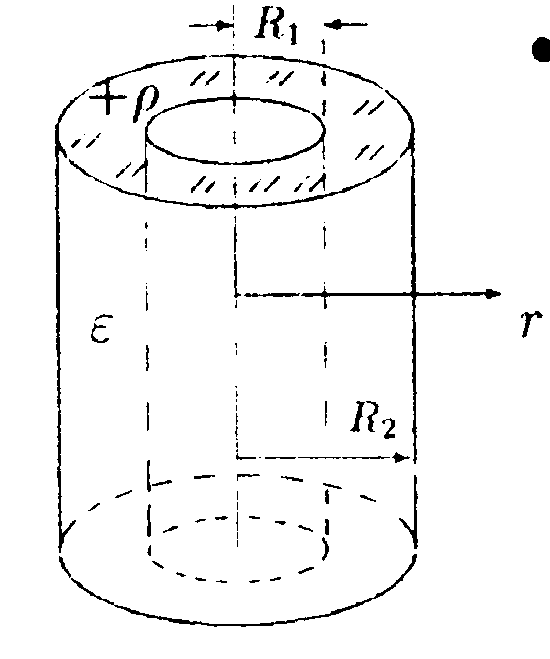




•5.15.7. Полый стеклянный цилиндр равномерно
заряжен с объемной плотностью заряда +р.
Внешний радиус цилиндра равен R2, внутрен­ний — R1. Используя теорему Гаусса, найдите зависимость напряженности Е и электрического смешения Dот расстояния r от оси цилиндра. Постройте графики зависимостей Е(r) и D(r). Диэлектрическая проницаемость стекла равна ε.

5.16 . Вариант 16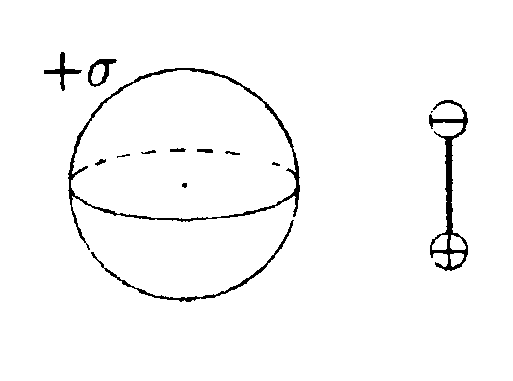

•

5.16.1. Электрический диполь помешен в поле,
созданное сферой равномерно заряженной с по­верхностной плотностью заряда +σ. Что будет
происходить с диполем? Как изменится сила вза­имодействия, если этот же заряд равномерно
распределить по всему объему сферы?

• 
  5.16.2. Три одинаковых заряда величиной q = 1,0·10ˉ⁹Кл каждый распо­ложены в вершинах прямоугольного треугольника, имеющего катеты:
  а = 40 см иb = 30 см. Найдите напряженность электростатического
  поля, создаваемого всеми зарядами в точке пересечения гипотенузы с
  перпендикуляром, опущенным на нее из вершины прямого угла.
  
• 
  5.16.3. Две одинаковые круглые пластины площадью S = 400 см² ка­ждая расположены параллельно друг другу. Заряд одной пластины
  Q_{ = 400 нКл. другой Q₂ =-200 нКл. Определите силу взаимного
  притяжения пластин, если расстояние между ними: а) r1 = 3,0 мм:
  б) r₂ = 9.0 м.
  

•

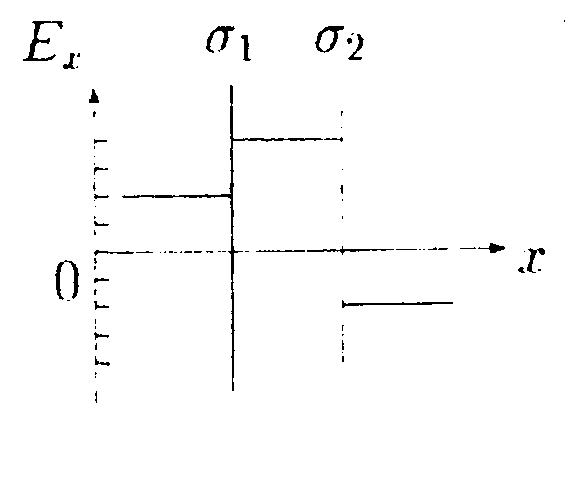5.16.4. На рисунке показано распределение на­пряженности электростатического поля Е_х(х).
созданного двумя параллельными заряженными
бесконечными пластинами, вдоль направления х.
Как различаются поверхностные плотности за­
рядов σ1и σ2 на этих пластинах по знаку и по
модулю?

• 
  5.16.5. Укажите, в каких из представленных случаев поток вектора
  электрического смещения через замкнутую поверхность не равен нулю:
  а) в области, ограниченной замкнутой поверхностью, находится элек­трический диполь; б) поверхность охватывает часть заряженной нити;
  в) поверхность расположена внутри заряженного проводника.
  
• 
  5.16.6. Используя принцип суперпозиции, найдите напряженность элек­тростатического поля в центре круга, на который опирается полусфера
  радиусом R, равномерно заряженная с поверхностной плотностью за­ряда α .
  
• 
  5.16.7. Бесконечно длинный цилиндр радиусом Rравномерно заря­
  жен по объему с объемной плотностью заряда +р. Используя теорему
  Гаусса, найдите зависимость напряженности электростатического поля
  Е от расстояния г от оси цилиндра. Постройте график зависимости
  Е(r). Диэлектрическая проницаемость материала цилиндра равна ε.
  

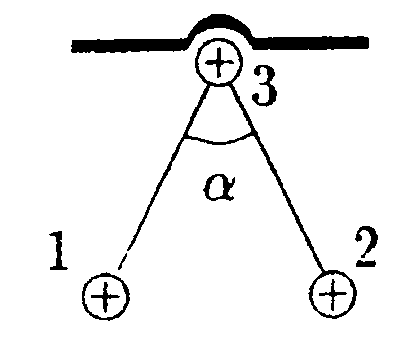
5.17 Вариант 17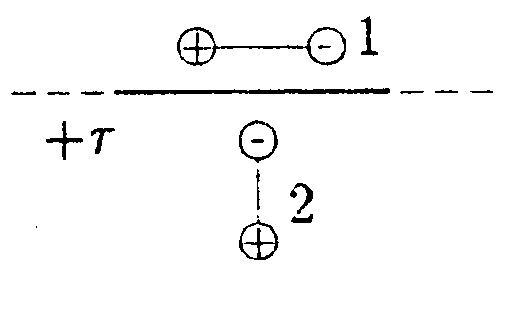

•

5.17.1. Что будет происходить с диполями 1 и
2, помещенными в поле бесконечной нити, рав­номерно заряженной с линейной плотностью за­ряда +r?

• 
  5.17.2. Два заряда q1 = +4,5qи q2=-0,5qнаходятся на расстоянии
  l= 10 см. Третий заряд, модуль которого |qз| = q, может перемещаться
  вдоль прямой, проходящей через заряды q1 и q2. Определите положение
  заряда q₃, при котором он будет находиться в равновесии. При каком
  знаке заряда равновесие будет устойчивым?
  
• 
  5.17.3. С какой силой (на единицу длины) взаимодействуют две беско­нечно длинные параллельные нити, равномерно заряженные с одинаковой линейной плотностью заряда r=+20 мкКл/м находящиеся на
  расстоянии r= 10 см друг от друга?
  

•

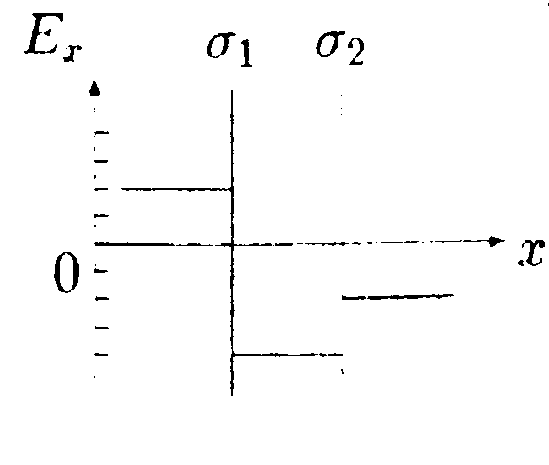5.17.4. На рисунке показано распределение напряженности электростатического поля Еx(x).
созданного двумя параллельными заряженными
бесконечными пластинами, вдоль направления х.
Как различаются поверхностные плотности зарядов σ1и σ2 на этих пластинах по знаку и по
модулю?

• 
  5.17.5. В зазор между разноименно заряженными
  плоскостями ввели пластину из диэлектрика, не
  имеющую свободных зарядов. Пунктиром на рисунке показана воображаемая замкнутая поверхность S, частично проходящая внутри диэлектрика, частично вне сто. Чему равен поток вектора электрического смешения Dчерез эту поверхность?
  
• 
  5
  
  .17.6. Два прямых тонких стержня длиной
  1.0 м каждый заряжены с линейной плотностью
  r = 3,0·10ˉ⁸ Кл/м. Стержни расположены перпендикулярно друг к другу. Используя принцип
  суперпозиции, найдите напряженность электростатического поля в точке А. удаленной от концов стержней, как показано на рисунке, на расстояние r= 0,5 м.
  
• 
  5
  
  .17.7. При пересечении двух шаров радиусами
  R, центры которых находятся на расстоянии l
  друг от друга, образуются два "полумесяца",
  равномерно заряженных с объемными плотностями зарядов -р и +р. Докажите, что электростатическое поле в области пересечения шаров однородно. Найдите напряженность этого поля.
  

5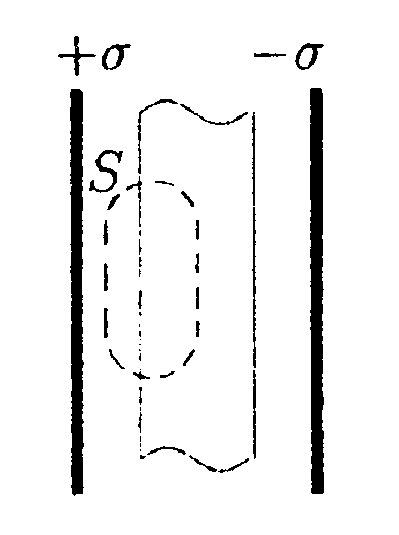

.18, Вариант 18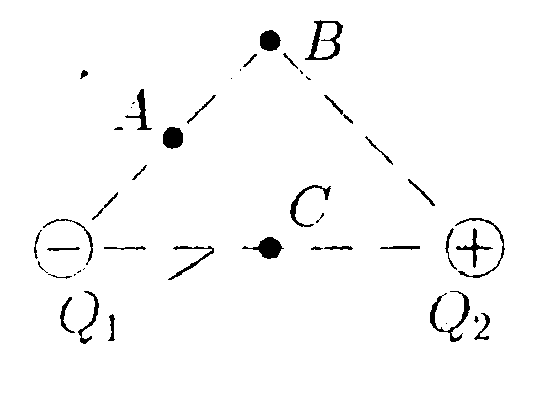



5.18.1. Поле создается равными по модулю за­рядами Q₁и Q₂, расположенными в вершинах равностороннего треугольника. Укажите напра­вление векторов напряженности электростати­ческого поля в точках A, В, С. Точки Aи С расположены на середине сторон треугольника. Сравните модули результирующих векторов на­пряженности в указанных точках.

• 5.18.2. Электростатическое поле создано двумя точечными зарядами q1 = +q, |q2| = 2q, находящимися в точках В и С на прямой AD. Где на прямой ADнаходится точка, в которой напряженность результиру­ющего поля равна нулю? Рассмотрите случаи: a) q2> 0; б) q2< 0.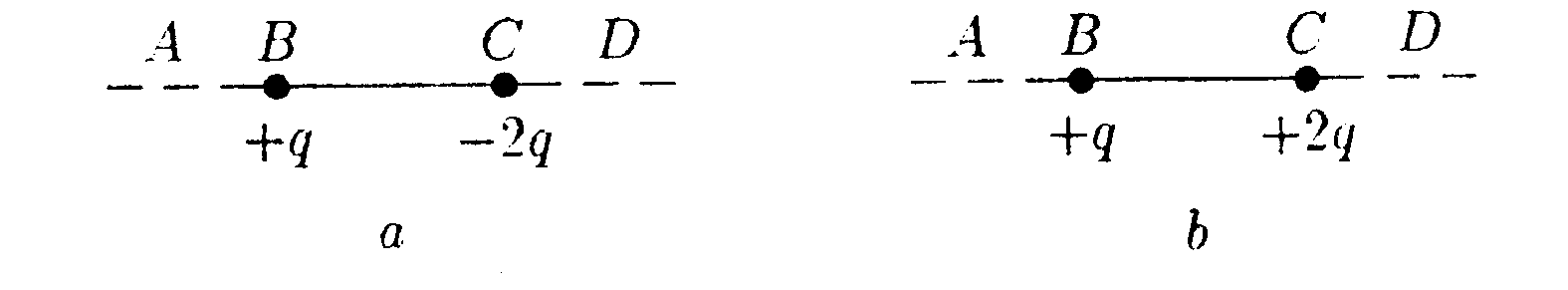

•

5.18.3. Бесконечная равномерно заряженная плоскость имеет поверх­ностную плотность заряда а = +9,0·10ˉ⁶ Кл/м². Над ней находится алюминиевый шарик с зарядом q = 3,7·10⁷Кл. Каким должен быть радиус шарика, чтобы он не падал? Расстояние до плоскости много больше радиуса шарика, плотность алюминия р = 2,6 • 10³кг/м³.

• 
  5
  
  .18.4. На рисунке показано распределение напряженности электростатического поля Е_х(х),
  созданного двумя параллельными заряженными
  бесконечными пластинами, вдоль направления х.
  Как различаются поверхностные плотности зарядов σ1и σ2на этих пластинах по знаку и по модулю?
  
• 
  5
  
  .18.5. Поле в вакууме создается системой оди­наковых по модулю зарядов |q|= 1,0·10ˉ⁸Кл. Найдите потоки векторов напряженности Е и электрического смещения Dчерез произвольную замкнутую поверхность S. окружающую заряды. Как изменятся потоки, если систему зарядов по­местить в среду с диэлектрической проницаемо­стью ε = 2,0?
  

•

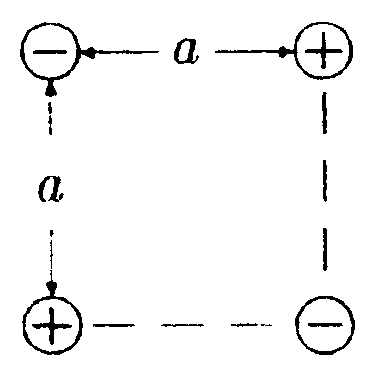
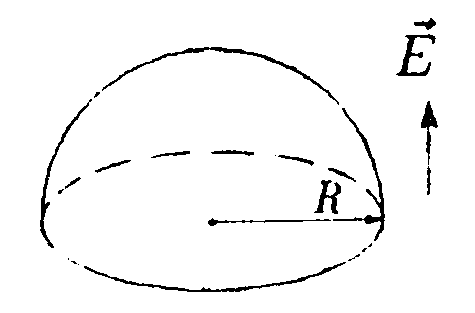
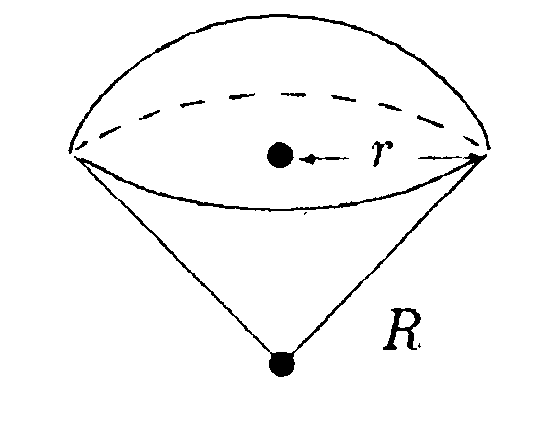5.18.6. Используя принцип суперпозиции, дока­жите, что напряженность электростатического поля равномерно заряженного сферического сег­мента в центре его кривизны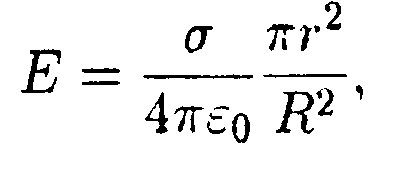





где σ - поверхностная плотность заряда сег­мента, r - радиус круга в основании сегмента, R- радиус сферы, из которой вырезан сегмент.

• 5.18.7. Две длинные тонкие проводящие нити расположены параллельно друг другу на расстоянии d= 16 см. Нити равномерно заряжены разно­именными зарядами с линейной плотностью заряда |r| = 150 мкКл/м. Используя теорему Гаусса, найдите напряженность электростатиче­ского поля в точке, удаленной на расстояние а = 10 см от каждой нити.


6 . Тема: Потенциал. Работа. Энергия электрического поля

6.1 Вариант 1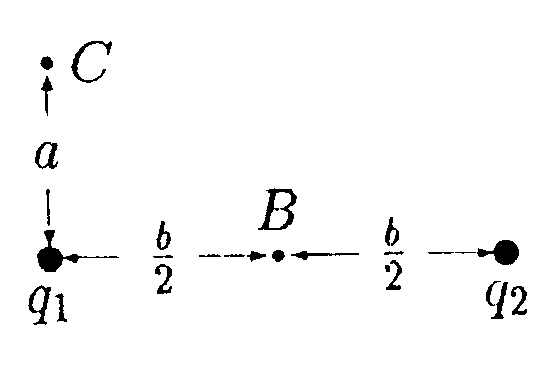

• 6.1.1. Определите работу электрических сил по
переносу пробного заряда q =1.0 • 10ˉ⁹Кл из
точки С в точку В, если а = 3,0 см, b = 4,0 см,
q1= 3,3 • 10ˉ⁹Кл, q2= -3,3 • 10ˉ⁹Кл.

• 6.1.2. Около заряженной бесконечно протяженной плоскости находится
точечный заряд q=0,66 нКл. Заряд перемещается по линии напря­женности поля на расстояние l= 2.0 см. При этом совершается работа
А = 5,0 • 10ˉ⁷Дж. Найдите поверхностную плотность заряда а на плос­кости.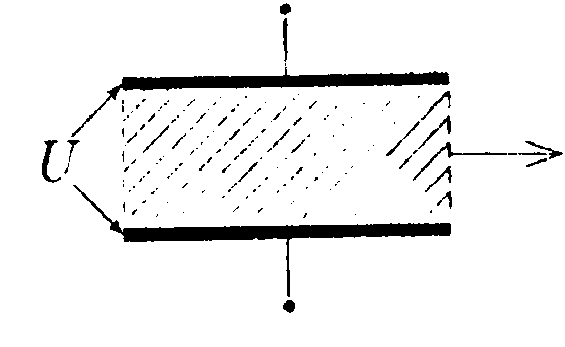

•

6.1.3. Найдите работу, которую нужно затра­тить, чтобы вынуть диэлектрик из плоского кон­денсатора, если напряжение на пластинах под­держивается постоянным и равным U = 500 В.
Площадь пластин S = 50 см², расстояние между
пластинами d = 0,50 см. а диэлектрическая про­ницаемость диэлектрика ε = 2,0.

• 6.1.4. На какое расстояние rмогут сблизиться два электрона, если

они движутся навстречу друг другу с относительной скоростью V = 1.0 · 10⁷ м/с?

• 6.1.5. Потенциал поля, создаваемого некоторой системой зарядов, имеет
вид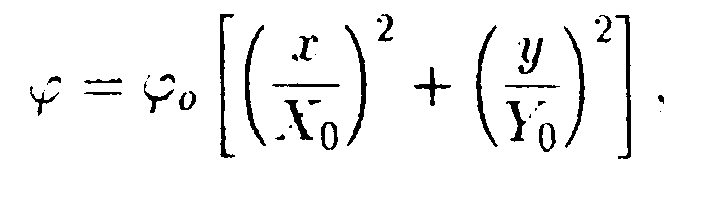




где φ₀= 1000 В, X0= 4,0 м, Y0= 9,0 м. Изобразите примерный вид си­ловых и эквипотенциальных линии и найдите напряженность электро­статического поля Е в точке С с координатами х_с = 2,0 м, у_с = 6,0 м.

• 
  6.1.6. Металлический шар радиусом R1 = 2,0 см имеет заряд q1 =2,0 • 10ˉ⁹ Кл. Шар окружен концентрической металлической оболочкой радиусом R2 = 5,0 см, равномерно заряженной зарядом q₂ = -4,0•10^-9 Кл. Найдите напряженность электрического поля Е и его потенциал φ на расстояниях r1= 1,5 см, r₂ = 3,0 см и r₃ = 7,0 см от центра шара.
  
• 
  6.1.7. Обкладки конденсатора с неизвестной емкостью С1, заряженного
  до напряженияU1= 80 В, соединяют с обкладками конденсатора емко­стью C2 = 60 мкФ, заряженного до напряжения U2= 16 В. Определите емкость С1, если напряжение на конденсаторах после их соединения U = 20 В. Конденсаторы соединяются обкладками, имеющими: а) од­ноименные заряды; б) разноименные заряды.