Сборник заданий. Сборник заданий Республиканской олимпиады по общеобразовательным. Сборник заданий Республиканской олимпиады по общеобразовательным предметам
 Скачать 2.33 Mb. Скачать 2.33 Mb.
|
 Областной учебно-методический центр по выявлению и поддержке одаренных детей и талантливой молодежи «Жетісу дарыны» управления образования Алматинской области Областной учебно-методический центр по выявлению и поддержке одаренных детей и талантливой молодежи «Жетісу дарыны» управления образования Алматинской областиСБОРНИК заданий Республиканской олимпиады по общеобразовательным предметам (естественно-математическое и общественно-гуманитарное направление) 9-11 классы Талдыкорган 2021 г. Собрали и отредактировали: Г.К.Рахимжанова, Т.Н.Оразалиева- методисты областного учебно-методического центра по выявлению и поддержке одаренных детей и талантливой молодежи «Жетісу дарыны» управления образования Алматинской области. В сборнике заданий собраны задания Республиканской олимпиады по общеобразовательным предметам, разработанные Республиканским научно-практическим центром «Дарын». Сборник может служить основой при подготовке учащихся средней школы и специализированных организаций образования к областному этапу республиканской олимпиады. СОДЕРЖАНИЕ Естественно –математическое направление Математика................................................................................4 Физика.......................................................................................10 Химия........................................................................................17 Биология....................................................................................49 География..................................................................................68 Общественно-гуманитарное направление Русский язык и литература .....................................................92 Русский язык и литература (в казахских классах)...............105 Английский язык.....................................................................109 История Казахстана.................................................................134 Основы права...........................................................................140 Самопознание..........................................................................155 ЕСТЕСТВЕННО-МАТЕМАТИЧЕСКОЕ НАПРАВЛЕНИЕ МАТЕМАТИКА Имеются две кучки камней: в первой 2012 монет, во второй – 2021 монета. Арман и Бахытжан играют в такую игру. За один ход игрок из любой кучки берёт 2, 3 или 4 монеты, а затем добавляет 1 монету во вторую кучку. Проигрывает тот игрок, который не может сделать ход. Арман и Бахытжан ходят по очереди. Начинает Арман. Кто выигрывает при правильной игре? Дан прямоугольный треугольник ABC с гипотенузой AB. Прямая, проходящая через точку D, середину гипотенузы AB, пересекает прямые AC и BC соответственно в точках P и Q. Пусть M – середина отрезка PQ. Из точки R, симметричной точке D относительно точки M, проведён перпендикуляр RF на гипотенузу AB. Докажите, что CM является биссектрисой угла FCD. Найти все пары (x,y) натуральных чисел, которые удовлетворяют уравнению 125 · 2х – 3y = 271. Изначально все клетки доски 2021 × 2021 белые. Арман и Бахытжан играют в такую игру. Сначала Арман закрашивает n квадратиков в красный цвет. Затем Бахытжан выбирает 1011 строк и 1011 столбцов и перекрашивает все ячейки в выбранных строках и столбцах в чёрный цвет. Арман выигрывает в том случае, если осталась хотя бы одна красная клетка, в противном случае выигрывает Бахытжан. При каком наименьшем n Арман гарантирует себе победу, независимо от того, как будет действовать Бахытжан. Дан треугольник ABC, в котором 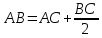 . На стороне BC отметили точки P, Q и R так, что BP = PQ = QR = RC. Прямые AP и AR пересекают серединный перпендикуляр к PQ соответственно в точках X и Y . На отрезке XY , как на диаметре, построена окружность Ω. Докажите, что Ω проходит через точки B и R. . На стороне BC отметили точки P, Q и R так, что BP = PQ = QR = RC. Прямые AP и AR пересекают серединный перпендикуляр к PQ соответственно в точках X и Y . На отрезке XY , как на диаметре, построена окружность Ω. Докажите, что Ω проходит через точки B и R.Покажите, что существует бесконечно много натуральных чисел n таких, что  также является натуральным числом. также является натуральным числом.Пусть a, b, c – положительные целые числа такие, что 20a2 +21b2 = 20a +21b. Найдите наименьшее значение выражения 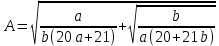 Многочлен P(x) с целыми коэффициентами таков, что P(1) = 17, P(m) = m2 + n2 − mn, P(n) = mn +1, где m, n – целые числа. Найти все возможные такие пары целых чисел (m,n). На плоскости нарисован четырёхугольник ABCD. Докажите, что на этой плоскости найдётся такая точка X, что квадрат расстояния от точки X, до самой удалённой от неё вершины четырёхугольника ABCD, не превосходит  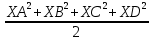 Пусть a, b, c – положительные целые числа такие, что 24a2 + 2b2 + 21c2 = 24a + 2b + 21c. Найдите наименьшее значение выражения 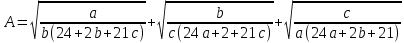 При каких натуральных n число (n − 1)! делится на 2021n2 ? Пусть a, b, c, d – положительные целые числа такие, что 24a2 + 2b2 + 20c2 + 21d2 = 24a + 2b + 20c + 21d Найдите наименьшее значение выражения 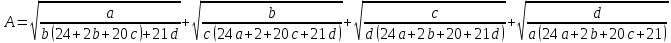 Дан остроугольный треугольник ABC, в котором ∠B < ∠C. Пусть I – центр вписанной окружности, O – центр описанной окружности, H – ортоцентр треугольника ABC. Пусть вписанная в треугольник ABC окружность касается стороны BC в точке D, и AO параллельна HD. Точка E – точка пересечения прямых OD и AH, точка F – середина отрезка CI. Докажите, что точки I, O, E и F лежат на одной окружности. При каких натуральных n число (n − 1)! делится на n3? Пусть a,b,c — положительные действительные числа такие, что 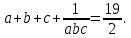 Найдите наибольшее возможное значение a. Найдите наибольшее возможное значение a.На полке стоят в беспорядке 100 томов энциклопедии, занумерованных всеми натуральными числами от 1 до 100. За одну операцию можно взять и любым способом переставить на своих местах любые три тома (т.е. если эти тома стояли в местах a,b,c, то после этой операции эти тома также будут стоять в местах a,b,c, но возможно в другом порядке). При каком наименьшем m можно утверждать, что m такими операциями удастся расставить все тома по порядку, как бы они ни были расставлены первоначально? (Тома стоят по порядку, если 1-й том стоит на 1-м месте, 2-й том на 2-м, ..., 100-й том на 100-м месте.) Продолжения сторон AB и CD выпуклого четырехугольника ABCD пересекаются в точке P, а диагонали AC и BD — в точке Q. Точки M и N — середины диагоналей AC и BD соответственно. Описанные окружности треугольников BCQ и MNQ пересекаются в точке T (T ≠ Q). Докажите, что если ∠APD = 90∘, то прямая PT делит отрезок MN пополам. Треугольник ABC (AC > BC) вписан в окружность ω. Биссектриса CN этого треугольника пересекает ω в точке M (M ≠ C). На отрезке BN отмечена произвольная точка T. Пусть H — ортоцентр треугольника MNT. Описанная окружность треугольника MNH пересекает ω в точке R (R ≠ M). Докажите, что ∠ACT = ∠BCR. Существуют ли натуральные числа a1, a2,...,a100 не обязательно различные), одновременно удовлетворяющие следующим условиям: число a1, a2,...,a100 делится на ai + aj при всех 1 ≤ i < j ≤ 100; для каждого k = 1,2,...,100 найдутся индексы i, j такие, что 1 ≤ i < j ≤ 100 и число a1, a2, ...ak-1, ak+1 ...a100 не делится на ai + aj? Дано натуральное число n. Последовательность (x 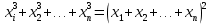 для каждого i = 1,2,...,n. Докажите, что количество различных хороших последовательностей не больше чем 3n-1 + 2n-1. (Последовательности (x для каждого i = 1,2,...,n. Докажите, что количество различных хороших последовательностей не больше чем 3n-1 + 2n-1. (Последовательности (xМожно ли разрезать клетчатый квадрат 100×100 на равное количество прямоугольников 2×4 и 1×8? (Фигурки можно поворачивать и переворачивать.) Дан треугольник ABC, в котором AB + AC > 3BC. Внутри этого треугольника отмечены точки P и Q такие, что ∠ABP = ∠PBQ = ∠QBC и ∠ACQ = ∠QCP = ∠PCB. Докажите, что AP + AQ > 2BC. Последовательности (an) и (bn) заданы условиями a1 = b1 = 1, an+1 = an + 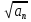 , bn+1 = bn + , bn+1 = bn +  . an ≤ bk < an+1 при всех натуральных n. Докажите, что существует натуральное число n, для которого неравенство an ≤ bk < an+1 выполнено ровно при 2021 значениях k. . an ≤ bk < an+1 при всех натуральных n. Докажите, что существует натуральное число n, для которого неравенство an ≤ bk < an+1 выполнено ровно при 2021 значениях k.На стороне AC треугольника ABC нашлась такая точка D, что BC = DC. Пусть J — центр вписанной окружности треугольника ABD. Докажите, что одна из касательных из точки J ко вписанной окружности треугольника ABC параллельна прямой BD. Найдите все функции f : R+ → R+ такие, что f(x)2 = f (xy) + f (x + f (y))−1 для любых x,y ∈ R+. (Здесь R+ — множество положительных действительных чисел.) Пусть a — натуральное число. Докажите, что для любого решения (x,y) уравнения x(y2 −2x2) + x + y + a = 0 в целых числах выполняется неравенство: |x|≤ a +  . .На полке стоят в беспорядке 100 томов энциклопедии, занумерованных всеми натуральными числами от 1 до 100. За одну операцию можно взять и любым способом переставить на своих местах любые три тома (т.е. если эти тома стояли в местах a,b,c, то после этой операции эти тома также будут стоять в местах a,b,c, но возможно в другом порядке). При каком наименьшем m можно утверждать, что m такими операциями удастся расставить все тома по порядку, как бы они ни были расставлены первоначально? (Тома стоят по порядку, если 1-й том стоит на 1-м месте, 2-й том на 2-м, ..., 100-й том на 100-м месте.) Докажите, что существует бесконечно много пар (a,b) натуральных чисел таких, что a ≠ b и для любого натурального n выполняется равенство  (Здесь [x] — целая часть числа x, то есть наибольшее целое число, не превосходящее x.) Внутри треугольника ABC взята такая точка M, что max(∠MAB,∠MBC,∠MCA) = = ∠MCA. Докажите, что sin∠MAB + sin∠MBC ≤ 1. Остроугольный треугольник ABC вписан в окружность Ω. В этом треугольнике проведены высоты AD, BE и CF. Прямая AD пересекает Ω вторично в точке P, а прямые PFи PEпересекают Ω вторично в точках R и Q соответственно. Пусть O1 и O2 — центры описанных окружностей треугольников BFRи CEQ соответственно. Докажите, что прямая O1O2 делит отрезок EF пополам. Пусть a — натуральное число. Докажите, что для любого решения (x,y) уравнения x(y2 −2x2) + x + y + a = 0 в целых числах выполняется неравенство: ||x| ≤ a +  Дан многочлен P(x) с действительными коэффициентами и натуральное число n. Известно, что для любого натурального m существует целое число l такое, что P(l) = mn. Докажите, что существуют действительные числа a, b и натуральное число k такие, что P(x) = (ax + b)k при всех действительных x. ФИЗИКА  Задача 1. Шар массой m, двигающийся поступательно со скоростью ν по гладкой горизонтальной поверхности, налетает на покоящийся шар массой 3m. Известно, что в момент прямо перед столкновением линия, соединяющая центры шаров, составляет с направлением начальной скорости налетающего шара угол =60°. Найдите модули скоростей ν1 и ν2 шаров после их абсолютно упругого удара, если трением можно полностью пренебречь. Задача 1. Шар массой m, двигающийся поступательно со скоростью ν по гладкой горизонтальной поверхности, налетает на покоящийся шар массой 3m. Известно, что в момент прямо перед столкновением линия, соединяющая центры шаров, составляет с направлением начальной скорости налетающего шара угол =60°. Найдите модули скоростей ν1 и ν2 шаров после их абсолютно упругого удара, если трением можно полностью пренебречь.Задача 2. Орбита некоторого небесного тела солнечной системы является вытянутой настолько, что его максимальное расстояние от Солнца равно радиусу орбиты Урана, а минимальное в точности совпадает с радиусом орбиты Марса. Рассчитайте период T обращения этого тела вокруг Солнца. Период обращения Марса и Урана вокруг Солнца составляют T1=1,88 года и T2= 84 года соответственно. Орбиты планет считайте круговыми.  Задача 3. Три идентичные батареи с Э.Д.С. ℰ соединены друг с другом, как указано на схеме, и нагружены сопротивлением R. Внутреннее сопротивление батарей намного меньше R. Какой ток протекает через сопротивление нагрузки? Задача 3. Три идентичные батареи с Э.Д.С. ℰ соединены друг с другом, как указано на схеме, и нагружены сопротивлением R. Внутреннее сопротивление батарей намного меньше R. Какой ток протекает через сопротивление нагрузки? Какие заряды появятся на проводящих шарах радиусами a (слева) и b (справа), если их соединить проводами с указанными на рисунке точками цепи? Расстояние между шарами значительно больше их радиусов.   Задача 4. Трубка массой M=80 г., длина которой равна L=1м, а поперечное сечение составляет S=0,3 см2 , имеет загнутый под прямым углом конец. Другой конец трубки с помощью резинового патрубка соединен с водопроводным краном. Найдите скорость истечения воды v плотностью p=1000 кг./м3 из трубки, если известен ее угол отклонения от вертикали α=200. Считайте, что резиновый патрубок имеет пренебрежимо малую упругость. Ускорение свободного падения равно ց=9,8 m/c2. Задача 4. Трубка массой M=80 г., длина которой равна L=1м, а поперечное сечение составляет S=0,3 см2 , имеет загнутый под прямым углом конец. Другой конец трубки с помощью резинового патрубка соединен с водопроводным краном. Найдите скорость истечения воды v плотностью p=1000 кг./м3 из трубки, если известен ее угол отклонения от вертикали α=200. Считайте, что резиновый патрубок имеет пренебрежимо малую упругость. Ускорение свободного падения равно ց=9,8 m/c2. Задача 5. На платформе установлен штатив с маятником в виде небольшого шарика на нити. Шарик много легче платформы. Сама же платформа вначале удерживается на наклонной плоскости, а затем ее отпускают и она соскальзывает по ней. Коэффициент трения платформы о плоскость µ, угол наклона плоскости α. На какой максимальный угол β отклонится от вертикали шарик в процессе движения платформы? Задача 5. На платформе установлен штатив с маятником в виде небольшого шарика на нити. Шарик много легче платформы. Сама же платформа вначале удерживается на наклонной плоскости, а затем ее отпускают и она соскальзывает по ней. Коэффициент трения платформы о плоскость µ, угол наклона плоскости α. На какой максимальный угол β отклонится от вертикали шарик в процессе движения платформы? Задача 6. Термос представляет собой сосуд с двойными стенками, пространство между которыми заполнено гелием. Известно, что расстояние между стенками, общая площадь поверхности которых составляет S=5ּ·10-2м-2, значительно меньше длины свободного пробега атомов гелия. В термос наливают воду массой mb=1кг при температуре кипения Т=373К, удельная теплоемкость которой составляет Сс=4200Дж/(кг·К). Гелий в колбе имеет давление ρ0=2Па при средней температуре  , где T0=297K– комнатная температура. Молярная масса гелия µ=4·10-3, универсальная газовая постоянная R=8,31 Дж/(моль·К). Используя приведенные характеристики, оцените время остывания кипяченой воды в термосе на ΔТ=5К . , где T0=297K– комнатная температура. Молярная масса гелия µ=4·10-3, универсальная газовая постоянная R=8,31 Дж/(моль·К). Используя приведенные характеристики, оцените время остывания кипяченой воды в термосе на ΔТ=5К . Задача 7. На столе лежит прямоугольная рамка с током I имеющая форму прямоугольника со сторонами a и b , ориентированными вдоль осей x и yсоответственно. Рамка находится в магнитном поле с составляющими (0, By, Bz). a) Покажите, что величина момента магнитных сил, действующих на рамку в описанном случае, равна M=IByS, где S – площадь рамки. Вокруг какой оси этот момент стремится повернуть рамку?  b) Покажите, что величина момента магнитных сил, действующих на произвольной формы рамку с током в магнитном поле, равна M=IB║S, где B║ – составляющая магнитного поля, лежащая в плоскости рамки, S – площадь рамки. b) Покажите, что величина момента магнитных сил, действующих на произвольной формы рамку с током в магнитном поле, равна M=IB║S, где B║ – составляющая магнитного поля, лежащая в плоскости рамки, S – площадь рамки. c) На какой угол от вертикали отклонится такая рамка с током (см. рис) в вертикальном магнитном поле B=0,1 Тл ? Все звенья рамки изготовлены из одинаковой проволоки. ABCD – квадрат со стороной a=20 см. Внутренние звенья соединяют середины сторон. Масса единицы длины проволоки ρ =40 г/м. Ток в рамке I=0,1 A . Ускорение свободного падения принять равным ց=9,8 м/с2 .  Задача 8. Среди трудов Уильяма Томсона нашли манускрипт с pV-диаграммой для идеального газа. На диаграмме был нарисован циклический процесс в виде треугольника KML, где угол при вершине M был прямым. Точка F изображенная на рисунке лежит на середине стороны KL. В данной точке, теплоемкость многоатомного газа равно нулю. Зная только точки M и F, восстановите данный цикл. Объем в точке K меньше чем в L. (Можно использовать только циркуль и линейку без делений). Задача 8. Среди трудов Уильяма Томсона нашли манускрипт с pV-диаграммой для идеального газа. На диаграмме был нарисован циклический процесс в виде треугольника KML, где угол при вершине M был прямым. Точка F изображенная на рисунке лежит на середине стороны KL. В данной точке, теплоемкость многоатомного газа равно нулю. Зная только точки M и F, восстановите данный цикл. Объем в точке K меньше чем в L. (Можно использовать только циркуль и линейку без делений). Задача 9. Три одинаковых конденсатора емкостью С , резистор сопротивлением R и диод D включены в схему, представленную на рисунке 3.1. Вольтамперная характеристика диода представлена на рисунке 3.2. Первоначально левый (на рисунке) конденсатор заряжен до напряжения U0, при этом заряд верхней пластины – положительный. Два других конденсатора не заряжены, ключ разомкнут. Затем ключ замыкают. Определите: a) напряжения на конденсаторах через большой промежуток времени после замыкания ключа; b) тепло, которое выделиться в схеме к этому моменту времени; c) тепло, выделившееся к этому моменту на диоде; d) тепло, выделившееся к этому моменту на резисторе.  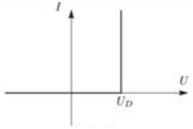 Рисунок 3.1 Рисунок 3.2 Экспериментальные задания І Задание. |
