Селевко. ПСиТ. Селевко. Селевко Г. К. Современные образовательные технологии Учебное пособие. М. Народное образование, 1998. 256 с
 Скачать 4.33 Mb. Скачать 4.33 Mb.
|
|
7.3. Укрупнение дидактических единиц - УДЕ (П.М. Эрдниев) Я выбрал борьбу против очевидностей, т.е. против всемогущества невозможностей. Л. Шестов Эрдниев Пюрвя Мучкаевич - академик РАО, заслуженный деятель науки РСФСР. Обосновал эффективность укрупненного введения новых знаний, позволяющего: - применять обобщения в текущей учебной работе на каждом уроке; - устанавливать больше логических связей в материале; - выделять главное и существенное в большой дозе материала; - понимать значение материала в общей системе ЗУН; - выявить больше межпредметных связей; - более эмоционально подать материал; - сделать более эффективным закрепление материала. Классификационные параметры По уровню применения: общепедагогическая. По основному фактору развития: социогенная. По концепции усвоения: ассоциативно-рефлекторная с элементами поэтапной интериоризации. По ориентации на личностные структуры: информационная с элементами операционной. По характеру содержания: обучающая, светская, технократическая, общеобразовательная. По типу управления: система малых групп. По организационным формам: классно-урочная, академическая, групповая -индивидуальная. По подходу к ребенку: дидактоцентрическая. По преобладающему методу: объяснительно-иллюстративная. По направлению модернизации: дидактическое реконструирование. По категории обучаемых: массовая + продвинутая. Целевые ориентации • Достижение целостности математических знаний как главное условие развития и саморазвития интеллекта учащихся. • Создание информационно более совершенной последовательности разделов и тем школьных предметов, обеспечивающее их единство и целостность. • Сверхзадача: вооружить девятилетнюю школу страны едиными учебниками математики (на базе рационального синтеза учебников алгебры, геометрии и черчения). Концептуальные положения Понятие «укрупнение единицы усвоения» достаточно общее, его можно представить как интеграцию конкретных подходов к обучению: 1) совместно и одновременно изучать взаимосвязанные действия, операции, функции, теоремы и т.п. (в частности, взаимно обратные); 2) обеспечение единства процессов составления и решения задач (уравнений!, неравенств и т.п.); 3) рассматривать во взаимопереходах определенные и неопределенные задания (в частности, деформированные упражнения); 4) обращать структуру упражнения, что создает условия для противопоставления исходного и преобразованного заданий; 5) выявлять сложную природу математического знания, достигать системности знаний; 6) принцип дополнительности в системе упражнений (понимание достигается в результате межкодовых переходов образного и логического в мышлении, сознательного и подсознательного компонентов). При этом используются фундаментальные закономерности мышления (вкупе оптимизирующие познавательный процесс): • закон единства и борьбы противоположностей; • перемежающееся противопоставление контрастных раздражителей (И.П.Павлов); • принцип обратных связей, системности и цикличности процессов (П.К.Анохин), обратимости операций (Ж.Пиаже); • переход к сверхсимволам, т.е. оперирование более длинными последователь ностями символов (кибернетический аспект). Укрупненная дидактическая единица - УДЕ - это локальная система понятий, объединенных на основе их смысловых логических связей и образующих целостно усваиваемую единицу информации. В отличие от гештальтистов П.М.Эрдниев рассматривает целостные образы, формирующиеся в результате обучения, как постаналитические. Им предшествует стадия анализа, разложения первоначально целостных образов, выделения в воспринимаемом объекте его элементов и их взаимоотношений. Обучение строится по следующей схеме: 1) Стадия усвоения недифференцированного целого в его первом приближении. 2) Выделение в целом элементов и их .взаимоотношений. 3) Формирование на базе усвоенных элементов и их взаимоотношений более совершенного и точного целостного образа. Особенности содержания В XX в. в школьном расписании встречались пять составляющих (предметов) единой науки математики: арифметика, геометрия, алгебра, тригонометрия, черчение, причем по некоторым предметам печаталось две книги (учебник и задачник). П.М.Эрдниев объединил в одном учебнике «Математика» все эти предметы, а также теорию и упражнения. В едином учебнике осуществляется синтез планиметрии и стереометрии, при этом классические разделы геометрии получают новую, координатную характеристику. В едином учебнике широко используются умозаключения по аналогии - важнейшему элементу творческого мышления. Упражнения приводятся по каждому логически завершенному параграфу (уроку, занятию). Учащимся предлагается: а) изучать одновременно взаимно обратные действия и операции: сложение и вычитание, умножение и деление, возведение в степень и извлечение корня, заключение в скобки и раскрытие скобок, логарифмирование и потенцирование и т.п.; б) сравнивать противоположные понятия, рассматривая их одновременно: прямая и обратная теоремы; прямая и противоположная теоремы; прямая и обратная функции; периодические и непериодические функции; возрастающие и убывающие функции; неопределенные и «определенные» уравнения: непротиворечивые и противоречивые уравнения, неравенства; прямые и обратные задачи вообще; в) сопоставлять родственные и аналогичные понятия: уравнения и неравенства, арифметические и геометрические прогрессии, одноименные законы и свойства действий первой и второй ступени; определения и свойства синуса и косинуса, свойства прямой и обратной пропорциональности и т.д.; г) сопоставлять этапы работы над упражнением, способы решения, на пример: графическое и аналитическое решение системы уравнений: аналитический и синтетический способы доказательства теорем (решения задач); геометрическое и аналитическое (через координаты) определение вектора; доказательство «рассуждением» и с помощью граф-схемы и т.п. Таким образом, главной особенностью содержания технологии П.М.Эрдниева является перестройка традиционной дидактической структуры материала внутри Учебных предметов, а в ряде случаев и внутри блока родственных учебных предметов. Особенности методики В качестве основного элемента методической структуры взято понятие «математическое упражнение» в самом широком значении этого слова, как соединяющее деятельность ученика и учителя, как элементарную целостность двуединого процесса «учения - обучения». Ключевой элемент технологии УДЕ - это упражнение-триада, элементы которой рассматриваются на одном занятии: а) исходная задача; б) ее обращение; в) обобщение. В работе над математическим упражнением (задачей) отчетливо выделяются четыре последовательных и взаимосвязанных этапа: а) составление математического упражнения; б) выполнение упражнения; в) проверка ответа (контроль); г) переход к родственному, но более сложному упражнению. Традиционное же обучение ограничивается большей частью вторым из указанных этапов. Опыт обучения на основе укрупнения единиц усвоения показал, что основной формой упражнения должно стать многокомпонентное задание, образующееся из нескольких логически разнородных, но психологически объединенных в некоторую целостность частей, например: а) решение обычной «готовой» задачи; б) составление обратной задачи и ее решение; в) составление аналогичной задачи по данной формуле (тождеству) или уравнению и решение ее; г) составление задачи по некоторым элементам, общим с исходной задачей; д) решение или составление задачи, обобщенной по тем или иным параметрам по отношению к исходной задаче. Разумеется, вначале в укрупненное упражнение могут войти лишь некоторые из указанных вариаций. Лейтмотивом урока, построенного по системе УДЕ, служит правило: не повторение, отложенное на следующие уроки, а преобразование выполненного задания, осуществляемое немедленно на этом уроке, через несколько секунд или минут после исходного, чтобы познавать объект в его развитии, противопоставить исходную форму знания видоизмененной. Методы обучения реализуются путем выполнения упражнений и объективируются в знаниях. При этом не одно только количественное разнообразие методов и упражнений важно само по себе. Лишь набор определенных упражнений, сконструированных на основе принципа укрупнения, в четкой их последовательности обеспечивает прочность и сознательность усвоения знаний. В технологии УДЕ используются одновременно все коды, несущие математическую информацию: слово, рисунок (чертеж), символ, число, модель, предмет, физический опыт. Литература 1. Селевко Г.К. Дидактические структуры учебного курса // Вопросы дидактики в техническом вузе. - Омск, 1985. 2. Эрдниев П.М. Обучение математике в начальных классах (из опыта работы). - М.: Просвещение, 1977. 3. Эрдниев П.М. Обучение математике в начальных классах (опыт обучения методом укрупнения дидактических единиц). - М.: Педагогика, 1979. 4. Эрдниев П.М. Обучение математике по УДЕ. Серия статей /У Начальная школа. -1993. -1996. 5. Эрдниев П.М. Укрупнение дидактических единиц как технология обучения. -М., 1992. 6. Эрдниев П.М. Укрупненные дидактические единицы на уроках математики в 1-2 классах. -М.: Просвещение, 1992. 7. Эрдниев П.М. Экспериментальное учебное пособие для 1, 2 класса. - М.: Педагогика, 1977. 8. Эрдниев П.М., Эрдниев Б.П. Теория и методика обучения математике в на чальной школе. -М.: Педагогика, 1988. 9. Эрдниев П.М., Эрдниев Б.П. Укрупнение дидактических единиц в обучении математике. -М., 1986. 7.4. Реализация теории поэтапного формирования умственных действий (М.Б. Волович) Человечество за многие тысячелетия своего существования все еще не научилось учиться. И.Ефремов Волович Марк Бенцианович — профессор московского педагогического университета, доктор педагогических наук. Классификационные параметры По уровню применения: частнопредметная. По основному фактору развития: социогенная. По концепции усвоения: интериоризаторская. По ориентации на личностные структуры: 1) ЗУН + 2) СУД. По характеру содержания: обучающая, светская, общеобразовательная. По типу управления познавательной деятельностью: программное управление. По организационным формам: все формы. По подходу к ребенку: дидактоцентрическая. По преобладающему методу: программированное обучение. По направлению модернизации: на основе методического усовершенствования и дидактического реконструирования материала. По категории обучаемых: все категории. Целевые ориентации • Эффективное усвоение программных ЗУН. Концептуальные положения И.П.Павлов: ориентировочный инстинкт всегда предшествует появлению рефлекса (знания). Л.С.Выготский: мышление - результат интериоризации практических действий и свойственной им логики. П.Я.Гальперин: понятие ориентировки переносится во внутренние психические процессы, мышление рассматривается как "свернутый в языке" процесс внешней предметной деятельности (см. п. 2.3.). Интериоризация (присвоение) деятельности в онтогенезе происходит в четыре этапа: 1) материальное действие с реальными предметами; 2) действие в громкой речи с образами (без предметов); 3) действие «во внешней речи про себя» (четко осознаваемое); 4) действие «во внутренней речи без слов» (неосознаваемое). Обучение основано на деятельности с использованием ориентировочной основы действий (ООД). Возможны 3 типа соотношения ООД и ученья (системы исполнения заданий - СИ): 1) При недостающей информации (ООД < СИ) получаются методы проб и ошибок, догматические. 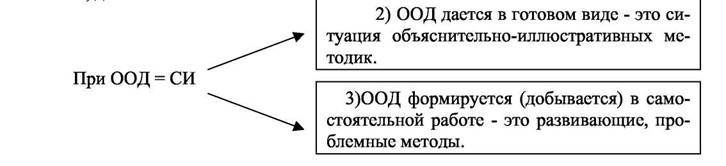 Успешность усвоения обеспечивается правильной организацией ориентировочной основы действий. Особенности содержания и методики Вычленив некоторую порцию материала, математическое содержание которого дети должны усвоить, учитель обдумывает, какая именно организация работы учеников соответствует этому материалу. Основная цель этапа первоначального знакомства - подготовить школьников к самостоятельному выполнению нужной работы, и сразу ее организовать. С точки зрения традиционной педагогики ситуация весьма странная: дети еще ничего не знают, а уже должны начинать работать с новыми знаниями. С точки зрения теории Гальперина ситуация ординарная: надо предоставить в распоряжение детей такие краткие схематические записи - конспекты материала и способов работы с ним, которые позволяют, ничего предварительно не заучивая, непосредственно после разъяснений учителя, приступить к самостоятельной работе с новыми заданиями. При традиционном обучении учитель, закончив объяснение, обычно просит задавать вопросы. Но их, как правило, не бывает: ученику трудно разобраться, все ли ему понятно. Рассматриваемая схема организации обучения предусматривает, что каждый ученик выполняет своеобразные тесты - работу с конспектами. В результате он имеет возможность убедиться, что материал ему понятен, либо у него возникают вопросы, на которые учитель отвечает непосредственно в ходе объяснения. Школьнику может показаться, что тест выполнен правильно, в действительности же он допустил ошибку. Чтобы этого не произошло, предусмотрена проверка правильности выполнения тестов. Каждый ученик получает шанс избавиться от недочетов в понимании объяснения. Носителями тестов являются тетради с печатной основой. Гальперин назвал первый этап усвоения этапом ориентировки в материале и способах работы с ним. Конспекты подлежащего усвоению материала он называет ориентирами, а конспекты, которые выдаются ученикам в ходе объяснения, ориентировочными картами. «В проблеме интеллектуальных возможностей ребенка существенное, если не решающее, значение получает четкость и уверенность ориентировки ребенка в задаче и материале действия. Когда ориентиры четко и устойчиво представлены на ориентировочной карте, ребенок уверенно ищет их (и только их!) и его не сбивают даже самые яркие, можно сказать, навязчивые свойства и отношения вещей. Поскольку они не отвечают признакам, указанным на ориентировочной карте, ребенок обходит их и обращается к тем признакам, которые не так заметны, но отвечают заданию. Более того, прочие свойства вещей, даже самые броские, дети начинают считать несущественными не только в данных заданиях, но и «вообще несущественными» (П.Я.Гальперин). В ТО учитель имеет возможность судить о правильности работы каждого из учеников в классе главным образом по конечному результату (после того, как работы учеников собраны и проверены). При данной технологии требуется, чтобы учитель проконтролировал каждый шаг работы каждого ученика. Контроль на всех этапах усвоения - один из важнейших компонентов технологии. Он направлен на то, чтобы помочь ученику избежать возможных ошибок. В учебном процессе используется четырехурочнын цикл. 1) Урок объяснения. Здесь важно создать у учеников определенный уровень мотивации и обеспечить ориентировочную основу действий с новым материалом. Для этого применяются различные методы актуализации базовых опорных знании: фронтальная беседа, сигнальные карточки, математические диктанты (с ТСО) ч. на конец, работа в тетради с печатной основой. Ориентировочная основа действий (ООД) дается в готовом виде и обеспечивает деятельность исполнения. 2) Урок решения задач. Предполагает дифференцированные и индивидуа лизированные варианты: реши с помощью, реши вместе с товарищем, реши само стоятельно. ООД = СИ варьируется от полной до недостаточно полной, подталкивая каждого ученика к самостоятельному решению. 3) Урок общения в форме взаимопроверки, групповой работы, работы в па рах. Каждый ученик отчитывается по всем основным теоретическим вопросам. При этом он использует различные варианты ориентировочной основы действий. 4) Самостоятельная работа организуется с помощью дидактических ма териалов и экспрессовых фронтальных способов контроля и самоконтроля. ООД формируется в самостоятельной работе, совершается постепенный переход от кон троля к самоконтролю. Литература 1. Воловик М.Б. Все это просто (о теории поэтапного формирования умственных действий) Народное образование. -1989. - № 10. 2. Волонич М.Б. Легкий предмет - математика (о теории поэтапного формирования умственных действий Гальперина)/ / Народное образование -1989 -№9. 3. Волович М.Б. Методические рекомендации учителю. - М.: Lmka-press, 1995 4. Волович М.Б. Наука обучать. - М.: Lmka-press. 1995. 5. Волович М.Б Система ориентиров - условие успешности обучения // Совет ская педагогика. -1988. -.№ 4. 6. Волович М.Б. Ключ к пониманию алгебры. — М : Аквариум, 1996. 7. Волович М.Б. Ключ к пониманию геометрии. — М., 1996. 8 .Гальперин П.Я. Методы обучения и умственное развитие ребенка. - М.: 1985. 9. Талызина Н.Ф. Формирование познавательной деятельности младших школьников. - М„ 1988. 10 Фридман Л.М.. Волков К.Н. Психологическая наука - учителю М.: Просвещение, 1995 VIII. Частнопредметные педагогические технологии Дидактические задачи конкретных учебных предметов решаются с помощью адекватных частно-предметных технологий обучения, целостность которых обеспечивается системностью научного содержания учебного предмета, а также выполнением в учебно-воспитательном процессе критериев технологичности (см. п. 2.2.). Частнопредметные технологии могут быть как обособленными, самостоятельными, так и встроенными в общешкольную технологию, иметь общую с ней концептуальную часть. 8.1. Технология раннего и интенсивного обучения грамоте (Н.А.Зайцев) Где это только возможно, обучение должно стать переживанием. А.Эйнштейн Зайцев Николай Александрович - педагог-новатор, академик Академии творческой педагогики, автор образовательных технологий, основанных на принципиально новых подходах к обучению грамоте и обеспечивающих высокую результативность. Комплекс оригинальных методических приемов, разработанных за 30 лет целенаправленной творческой деятельности Н.А.Зайцева, базируется на исследованиях классиков отечественной науки о человеке - И.М.Сеченова, И.П.Павлова, А.А.Ухтомского, В.М.Бехтерева и др. Сущность технологии Н.А.Зайцева в том, что он выстраивает учебный процесс на основах природосообразного развития ребенка, через отношение и деятельность, всесторонне активизируя познавательную мощь детского мозга. Н.А.Зайцев утверждает, что абстрактно-логическая неразвитость мозга ребенка компенсируется невиданной мощью восприятия импульсов, идущих от тактильности, зрения, слуха, обоняния, интуиции. Само по себе абстрактно-логическое, речевое отражение мира представляет только определенную часть возможностей интеллекта. И попытка опережающего использования именно этих возможностей, по мнению Н.А.Зайцева, приводит не к опережению в развитии целостной личности, а к замедлению его. Классификационные параметры технологии По уровню применения: частнопредметная. По основному фактору развития: социогенная. По концепции усвоения: ассоциативно-рефлекторная. По ориентации на личностные структуры: ЗУН - СУД. По характеру содержания: обучающая, светская, общеобразовательная, монотехнология. По типу управления: система малых групп - дифференциация + «репетитор». По организационным формам: классно-урочная + дифференцированная т индивидуальная. По подходу к ребенку: педагогика сотрудничества. По преобладающему методу: объяснительно-иллюстративная - игровая По направлению модернизации: альтернативная + природосообразная. По категории обучаемых: все категории. Целевые ориентации • Научить ребенка читать и считать в пределах ста к пяти годам. Концептуальные положения • Становление речи и обучение чтению должны идти параллельно, помогая одно другому. • Складовой принцип обучения чтению, отказ от фонемного принципа. • Соединение обучения с пением (запоминание складов в форме легких складо-вых песенок-напевок). • Путь к чтению лежит через письмо (от письма кубиками к чтению). • Использование всех видов памяти: звуковой, цветовой, объемной, моторной, кинестетической. • Восприятие всеми органами чувств, максимальная наглядность. • Названия букв не учатся, не употребляются никакие термины. Особенности содержания Игра-пособие «Кубики Зайцева» содержит 52 картонки, легко собирающиеся в кубики по навальцованным линиям, три листа таблиц и методическое руководство. Кубики различаются: - по 12 цветовым признакам (цвет, сочетание цветов, одно-двубуквенные склады с буквами трех цветов); - по объему; - по звучанию наполнителя («звучащие кубики Зайцева»); - по вибрации наполнителя; - по весу; - по сочетаниям признаков. По Зайцеву, склад - это «осознаваемое мускульное усилие речевого аппарата», каждая буква сама по себе, каждая согласная с последующей гласной или каждая согласная со знаками Ь и Ъ. Склады располагаются в таблицы, где они сопоставляются и соотносятся по звонкости, глухости, твердости и мягкости. Игра-пособие «Стосчет» («Миллиардер»). В пособие входят два набора картонных полос длиной 65 см по 10 шт. в каждом, с рядами чисел: от 0 до 9, от 10 до 19 ... от 90 до 99, шириной от 6 до 23 см (ширина полосы возрастает с увеличением значения числового ряда). Наборы отличаются тем, что в одном десяток представлен пирамидкой из кружочков, набранных как 4+3+2+1, в другом - двумя рядами квадратиков 5+5. Кроме того, есть две таблицы — белая и красная. Белая знакомит с употреблением знаков «+», «-», «=» на элементарных арифметических примерах, красная позволяет ребенку легко понять существо таких действий, как умножение и деление. Основная задача «Стосчета» кроме знакомства с цифрами, числами и четырьмя математическими действиями - представить любое число в пределах сотни в четырех его образах: звуковом, графическом (цифровом), количественном и компоновочном (возможности разложения одного числа на другие или, наоборот, составление). Особенности «Стосчета»: максимальная наглядность, логичность построения, позволяющая даже самым маленьким детям осваивать простейшие алгоритмы и производить математические действия с однои двузначными числами. Благодаря крупному размеру цифр не портится зрение, игра разработана и применяется так, что заставляет ребенка все время двигаться, стимулирует творческую активность. Особенности методики Весь «складовой запас» ювелирно разложен по полочкам - и на кубиках, и на столь же важных настенных таблицах. Каждому кубику соответствует столбик или строчка на таблицах. После кубиков ребята бегут к таблицам и водят по ним указкой, отыскивая нужные сочетания. В поисках одного они успевают перебрать и запомнить десятки. Блестящая систематизация позволяет очень быстро улавливать принципы подобия, алгоритмы поиска. А между делом ребята перебегают и к таблицам «Стосчета» и очень скоро научаются складывать и вычитать двузначные числа, осваивая объем арифметических навыков едва ли не до уровня третьего класса. Чем больше ребят, тем насыщенней общение и больше учителей у каждого. Последовательность тематики: 1. Твое имя. 2. Твои близкие. 3. Слово по выбору. 4. Что любим кушать. 5. Обед. 6. Магазин. 7. Зоопарк. 8. Поезд. 9. Дальнейшее расширение и усложнение содержания слов. 10. Предложения. Технологическая цепочка исполнения: 1. Показ учителя. 2. Ребенок действует с помощью руки учителя. 3. Ребенок работает сам. 4. Игры в слова, загадки, картинки. 5. Групповая работа, командная игра. Рекомендации: не говорить детям «Я буду учить вас читать» - это они сами учатся; не переусердствовать с помощью: ребенок должен незаметно перейти к самостоятельности. Имеются логопедические варианты методики. Литература 1.Зайцев Н. Сенсация? Трудно поверить? // Педагогический вестник. - 1994. -№1. 2. Зайцев Н.А. В помощь ученикам и родителям // Педагогический вестник. - 1995. - № 8. 3. Зайцев Н.А. Конспект методик по раннему обучению грамоте. 4. Зайиен Н.А., Струве Г.А. Читай и пой. - Челябинск, 1994. 5. Пижурина Н. Кубики Зайцева / /' Учительская газета. -1989. -13 июля. 6. Шарапова Е Читаем по Зайцеву / / Частная школа. -1995. - .N?3. 7. Шарыпова Е.У. У Зайцева и малыш грамотный / / Педагогический вестник. -1994, |
