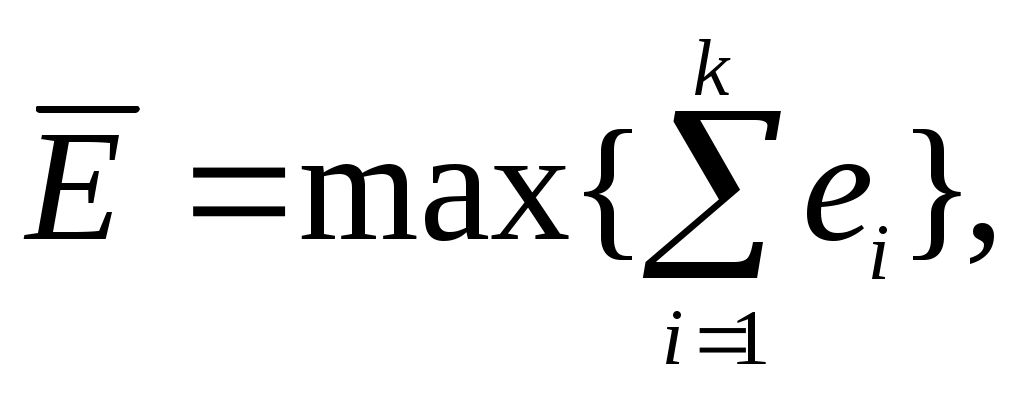Таблица П29. Оптимальный выпуск продукции по критерию 3
Товары
|
Товар 1
|
Товар 2
|
Товар 3
|
Товар 4
|
Товар 5
|
Товар 6
|
Товар 7
|
Товар 8
|
Доход
|
Количество (шт.)
|
0,00
|
0,00
|
0
|
0,00
|
15,12
|
0
|
0,00
|
29,54545
|
Цена (руб.)
|
25
|
23
|
10
|
22
|
18
|
19
|
24
|
20
|
863,0435
|
Таблица П30. Расход ресурсов на выпуск продукции по критерию 3
Ресурсы
|
Товар 1
|
Товар 2
|
Товар 3
|
Товар 4
|
Товар 5
|
Товар 6
|
Товар 7
|
Товар 8
|
Расход ресурса
|
Знак нера-венства
|
Наличие
|
Ресурс 1 (ед. измерения)
|
2
|
4
|
3
|
5
|
3
|
1
|
4
|
3
|
133,9921
|
<=
|
150
|
Ресурс 2 (ед. измерения)
|
0,5
|
0,7
|
0
|
0,8
|
0,3
|
0
|
0
|
0,6
|
22,26
|
<=
|
65
|
Ресурс 3 (ед. измерения)
|
12
|
24
|
30
|
0
|
0
|
10
|
15
|
22
|
650,00
|
<=
|
650
|
Ресурс 4 (ед. измерения)
|
5
|
7
|
9
|
1
|
3
|
4
|
5
|
2
|
104,4466
|
<=
|
200
|
Ресурс 5 (ед. измерения)
|
0
|
0
|
0
|
5
|
8
|
5
|
0
|
0
|
120,95
|
<=
|
320
|
Ресурс 6 (ед. измерения)
|
20
|
18
|
22
|
18
|
23
|
21
|
20
|
17
|
850
|
<=
|
850
|
Ресурс 7 (ед. измерения)
|
9
|
6
|
8
|
4
|
7
|
8
|
9
|
5
|
253,56
|
<=
|
600
|
Ресурс 8 (ед. измерения))
|
0
|
0,6
|
0,9
|
0,5
|
0,8
|
0,4
|
0,2
|
0,7
|
32,78
|
<=
|
490
|
Ресурс 9 (ед. измерения)
|
8
|
9
|
7
|
8
|
7
|
8
|
9
|
9
|
371,74
|
<=
|
700
|
Ресурс 10 (ед. измерения)
|
12
|
15
|
11
|
14
|
13
|
15
|
16
|
11
|
521,54
|
<=
|
750
|
Ресурс 11 (ед. измерения)
|
0,22
|
0,35
|
0,45
|
0,12
|
0,05
|
0,19
|
0,25
|
0,36
|
11,39
|
<=
|
220
|
Ресурс 12 (ед. измерения)
|
54
|
23
|
48
|
39
|
27
|
31
|
52
|
48
|
1826,383
|
<=
|
2100
|
Ресурс 13 (ед. измерения)
|
13
|
18
|
19
|
15
|
12
|
14
|
17
|
16
|
654,15
|
<=
|
1000
|
Ресурс 14 (ед. измерения)
|
2
|
4
|
2
|
1
|
5
|
7
|
1
|
3
|
164,23
|
<=
|
450
|
Ресурс 15 (ед. измерения)
|
27
|
25
|
20
|
24
|
18
|
24
|
25
|
22
|
922,1344
|
<=
|
1100
|
Очевидно, что оптимальное решение по одному критерию не совпадает с оптимальным решением по другим, т.е. критерии противоречивы. Задались вектором важности критериев 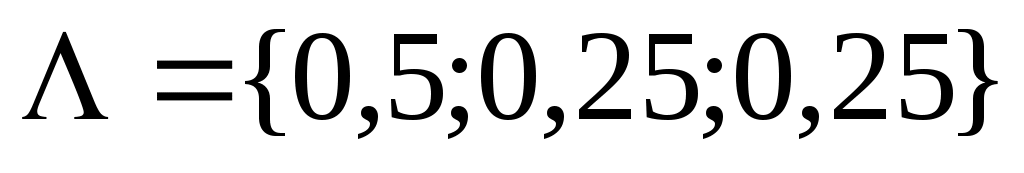 и решили задачу методом скаляризации векторного критерия воспользовавшись формулой: и решили задачу методом скаляризации векторного критерия воспользовавшись формулой:
 . .
Оптимальное решение при выбранной схеме компромисса и заданных значениях вектора важности имеет вид {21,18; 0; 0; 19,61; 3,19; 0; 0; 0}, а
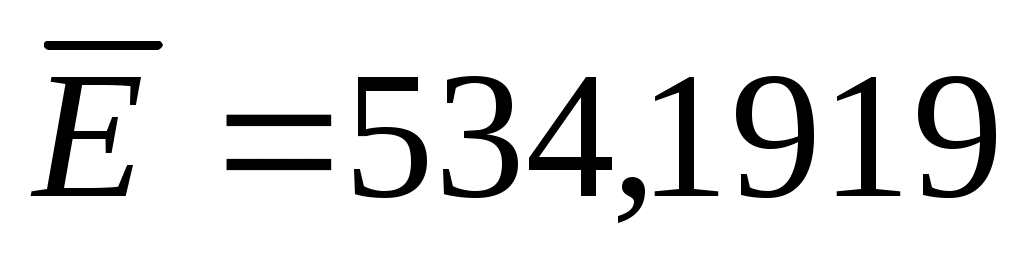 . .
Значения локальных критериев равны соответственно 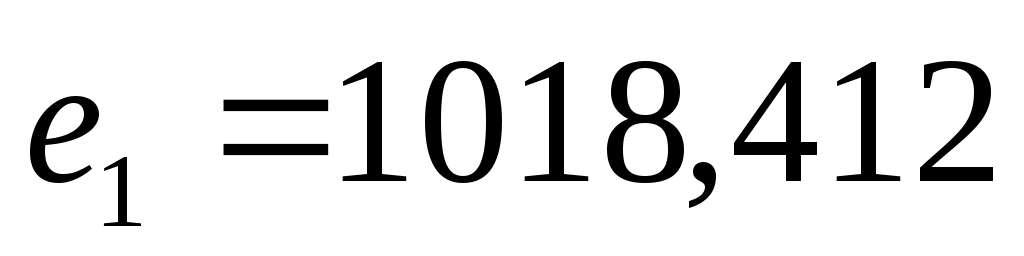 , , 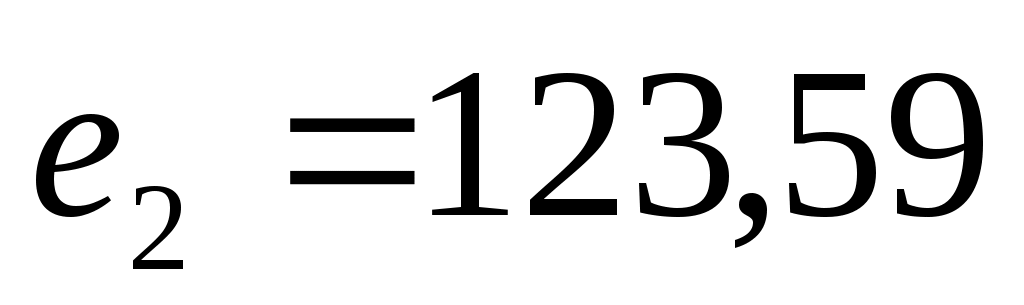 , , 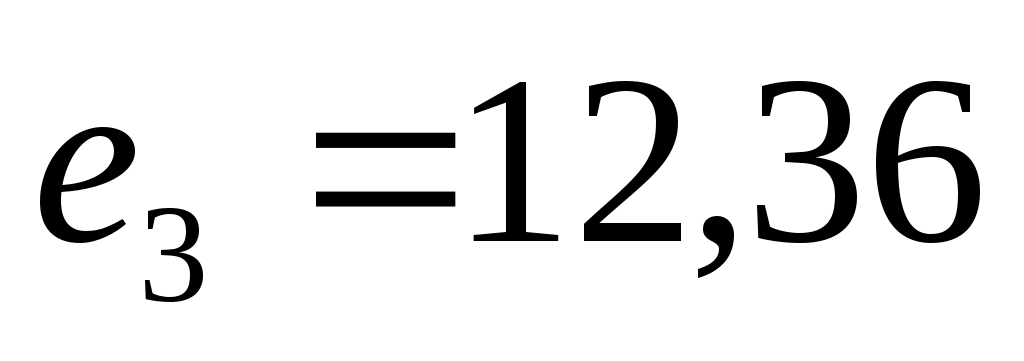 . .
При другом векторе важности 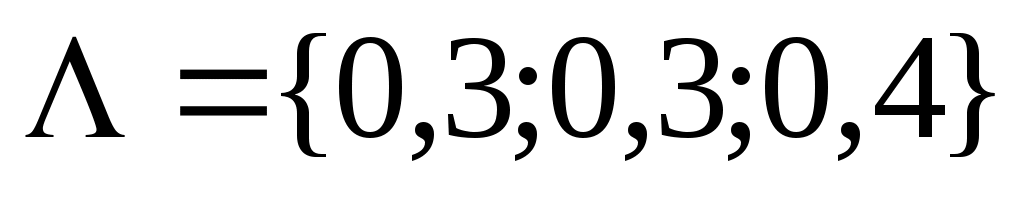 : :
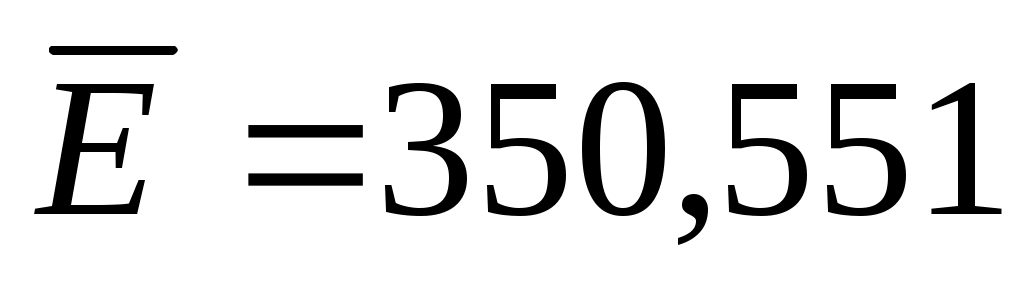 . .
При этом 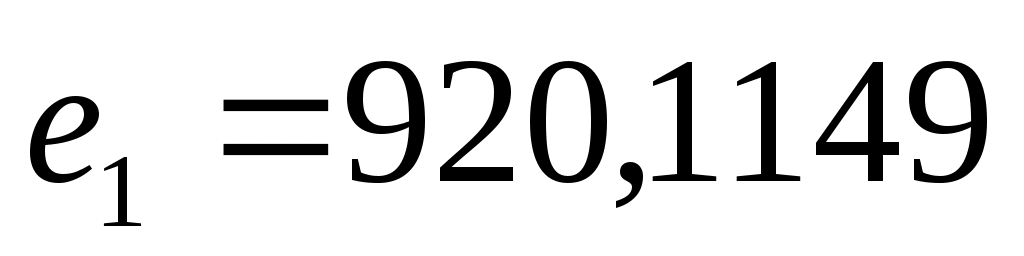 ; ; 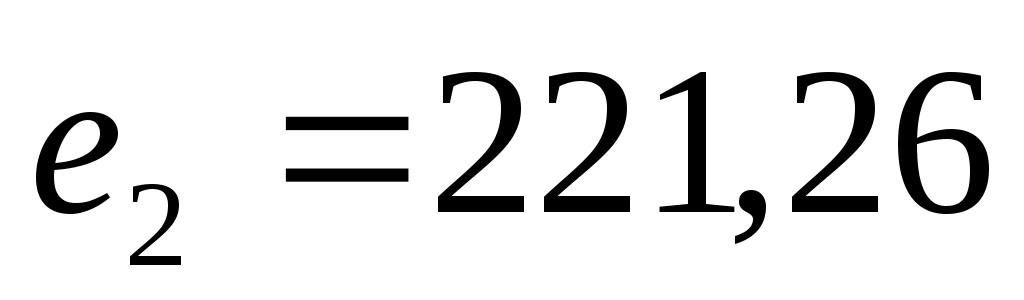 ; ; 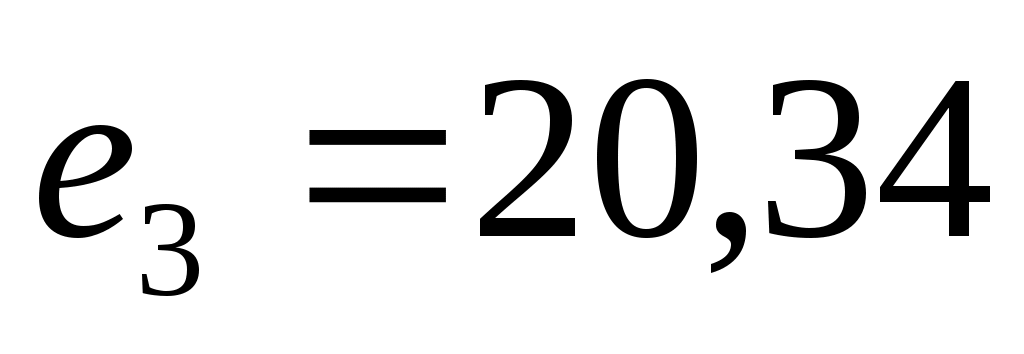 , а оптимальное решение имеет вид {0; 0; 0; 26,44; 0; 17,82; 0; 0}. , а оптимальное решение имеет вид {0; 0; 0; 26,44; 0; 17,82; 0; 0}.
Воспользовались методом квазиравенства, при реализации которого добиваются обеспечения разности между величинами локальных критериев, не превышающих некоторой заданной величины 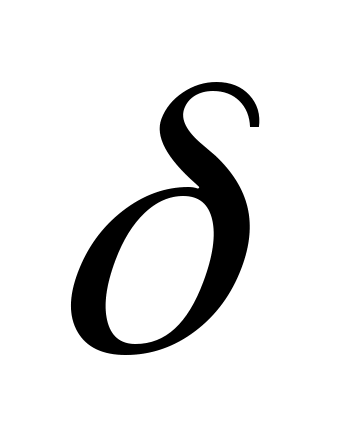 . Предположили, что все локальные критерии имеют одинаковые единицы измерения. Тогда . Предположили, что все локальные критерии имеют одинаковые единицы измерения. Тогда
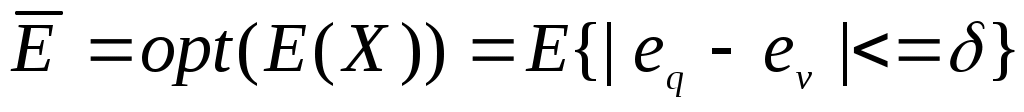 , , 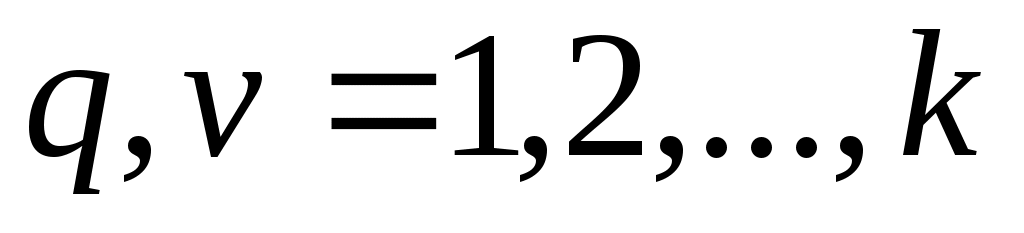 . .
Пусть 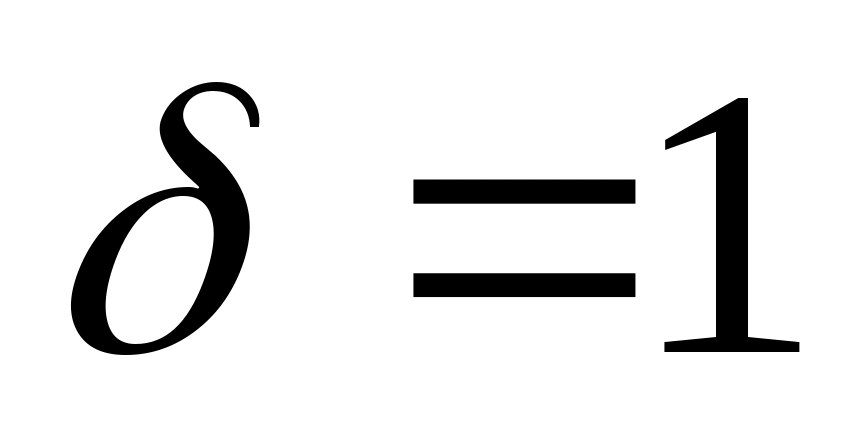 . Установили в качестве целевой ячейку, содержащую расчет дохода, а выражения . Установили в качестве целевой ячейку, содержащую расчет дохода, а выражения 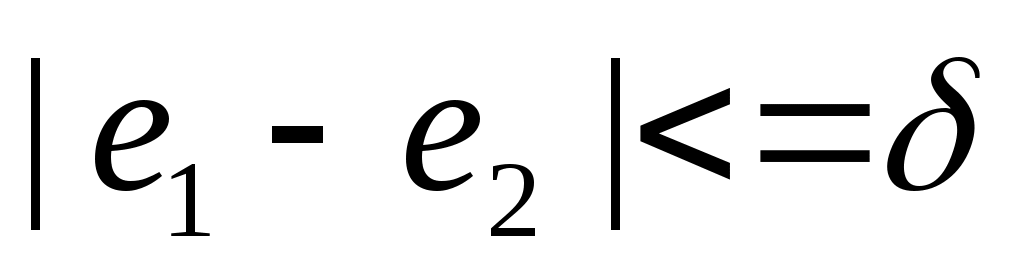 , , 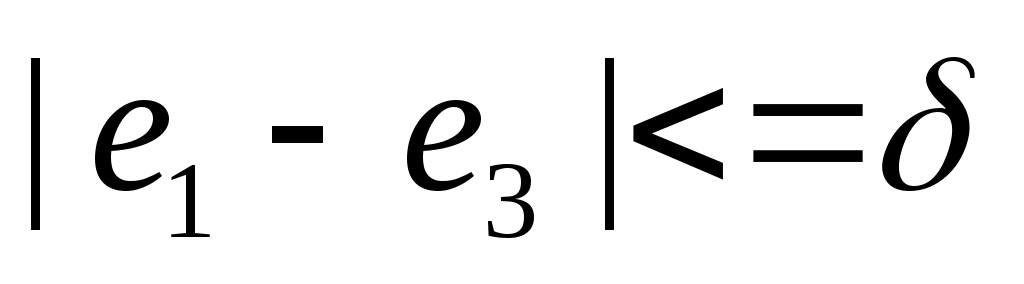 , , 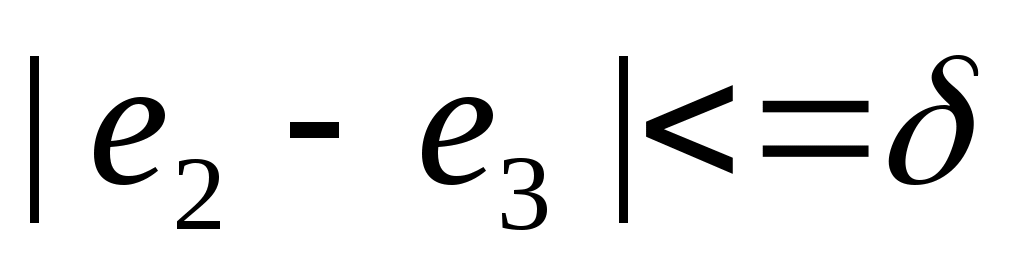 записали как дополнительные ограничения. Решая задачу оптимизации, получили таблицы П31 и П32: записали как дополнительные ограничения. Решая задачу оптимизации, получили таблицы П31 и П32:
Таблица П31. Оптимальный выпуск продукции по принципу квазиравенства
Товары
|
Товар 1
|
Товар 2
|
Товар 3
|
Товар 4
|
Товар 5
|
Товар 6
|
Товар 7
|
Товар 8
|
Доход 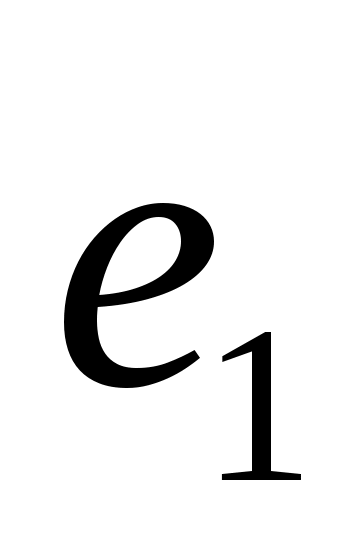
|
Критерий 2 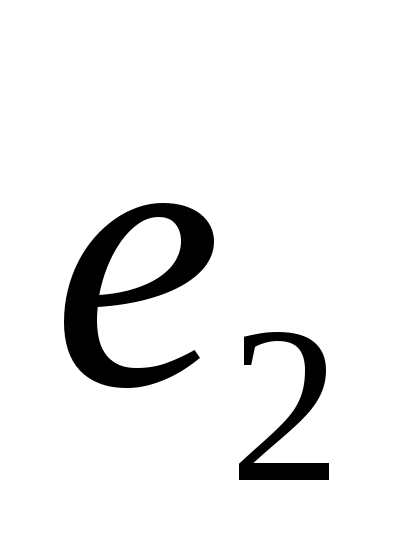
|
Критерий 3 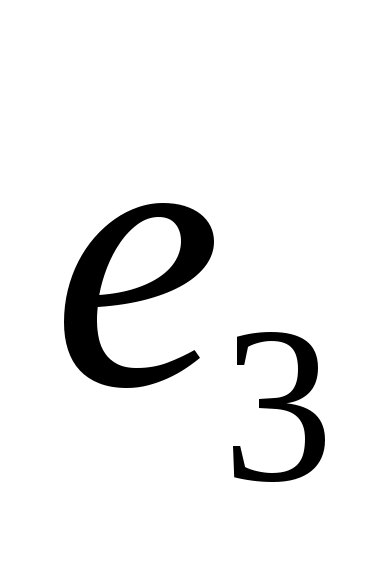
|
Количество (шт.)
|
0
|
0
|
0,088889
|
0
|
0,011111
|
0
|
0
|
0
|
Цена (руб.)
|
25
|
23
|
10
|
22
|
18
|
19
|
24
|
20
|
1,088888846
|
0,088889
|
0,088889
|
Таблица П32. Расход ресурсов на выпуск продукции по принципу квазиравенства
Ресурсы
|
Товар 1
|
Товар 2
|
Товар 3
|
Товар 4
|
Товар 5
|
Товар 6
|
Товар 7
|
Товар 8
|
Расход ресурса
|
Знак нера-венства
|
Наличие
|
Ресурс 1 (ед. измерения)
|
2
|
4
|
3
|
5
|
3
|
1
|
4
|
3
|
0,3
|
<=
|
150
|
Ресурс 2 (ед. измерения)
|
0,5
|
0,7
|
0
|
0,8
|
0,3
|
0
|
0
|
0,6
|
0,003333332
|
<=
|
65
|
Ресурс 3 (ед. измерения)
|
12
|
24
|
30
|
0
|
0
|
10
|
15
|
22
|
2,666666826
|
<=
|
650
|
Ресурс 4 (ед. измерения)
|
5
|
7
|
9
|
1
|
3
|
4
|
5
|
2
|
0,833333365
|
<=
|
200
|
Ресурс 5 (ед. измерения)
|
0
|
0
|
0
|
5
|
8
|
5
|
0
|
0
|
0,088888846
|
<=
|
320
|
Ресурс 6 (ед. измерения)
|
20
|
18
|
22
|
18
|
23
|
21
|
20
|
17
|
2,211111106
|
<=
|
850
|
Ресурс 7 (ед. измерения)
|
9
|
6
|
8
|
4
|
7
|
8
|
9
|
5
|
0,788888894
|
<=
|
600
|
Ресурс 8 (ед. измерения))
|
0
|
0,6
|
0,9
|
0,5
|
0,8
|
0,4
|
0,2
|
0,7
|
0,088888889
|
<=
|
490
|
Ресурс 9 (ед. измерения)
|
8
|
9
|
7
|
8
|
7
|
8
|
9
|
9
|
0,7
|
<=
|
700
|
Ресурс 10 (ед. измерения)
|
12
|
15
|
11
|
14
|
13
|
15
|
16
|
11
|
1,122222212
|
<=
|
750
|
Ресурс 11 (ед. измерения)
|
0,22
|
0,35
|
0,45
|
0,12
|
0,05
|
0,19
|
0,25
|
0,36
|
0,040555558
|
<=
|
220
|
Ресурс 12 (ед. измерения)
|
54
|
23
|
48
|
39
|
27
|
31
|
52
|
48
|
4,566666778
|
<=
|
2100
|
Ресурс 13 (ед. измерения)
|
13
|
18
|
19
|
15
|
12
|
14
|
17
|
16
|
1,822222259
|
<=
|
1000
|
Ресурс 14 (ед. измерения)
|
2
|
4
|
2
|
1
|
5
|
7
|
1
|
3
|
0,233333317
|
<=
|
450
|
Ресурс 15 (ед. измерения)
|
27
|
25
|
20
|
24
|
18
|
24
|
25
|
22
|
1,977777788
|
<=
|
1100
|
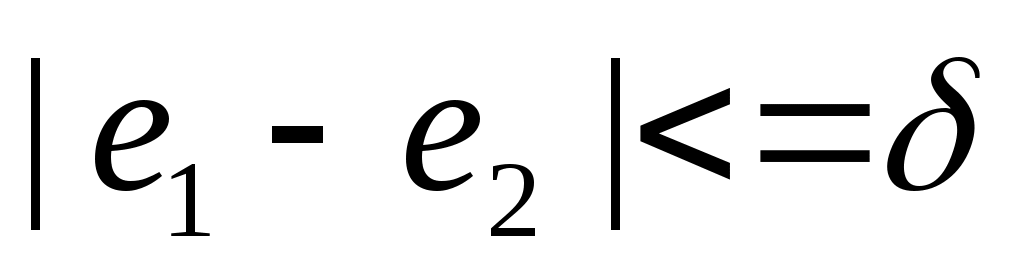
|
|
|
|
|
|
|
|
|
1
|
|
1
|
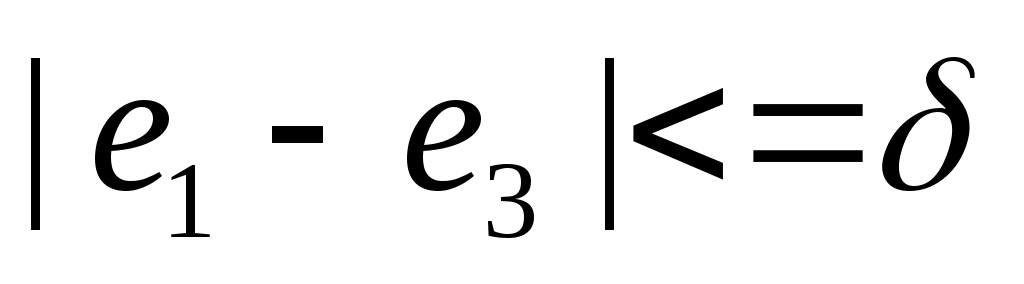
|
|
|
|
|
|
|
|
|
0,999999957
|
|
0,999999957
|
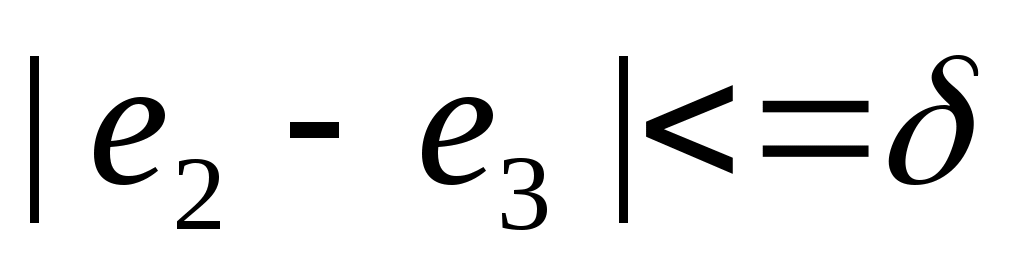
|
|
|
|
|
|
|
|
|
4,29969E-08
|
|
4,29969E-08
|
Решение задачи оптимизации по принципу максимина совпадает с решением при максимизации локального критерия 3 (таблица П29), поскольку он во всех трех случаях имеет минимальное значение.
Принцип абсолютной уступки соответствует критерию:
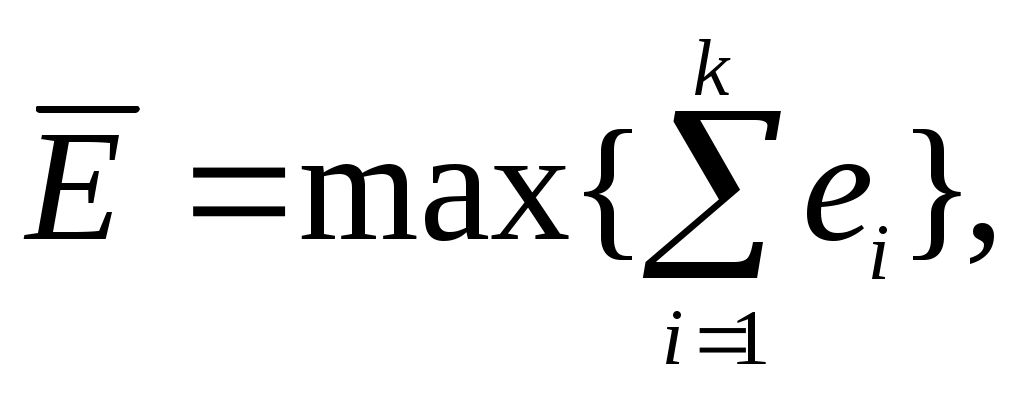
В нашем случае составляет 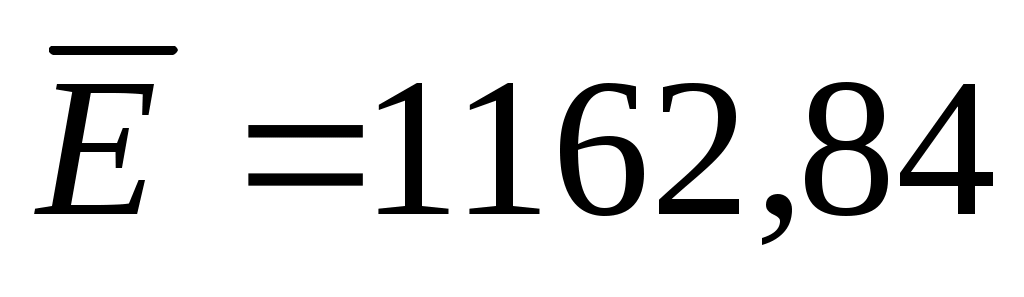 , при этом , при этом 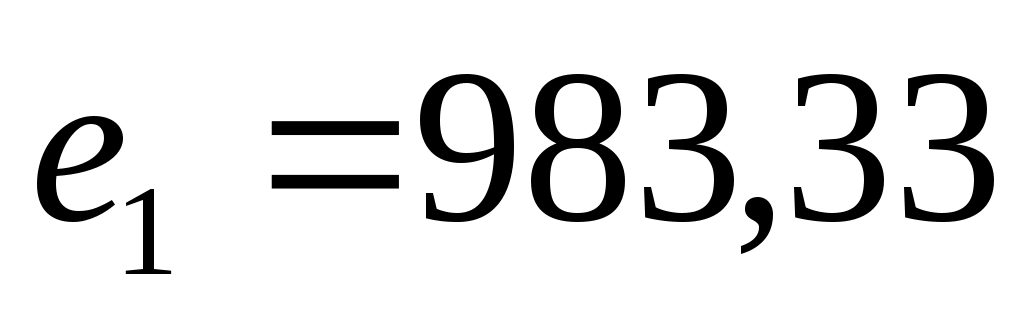 , , 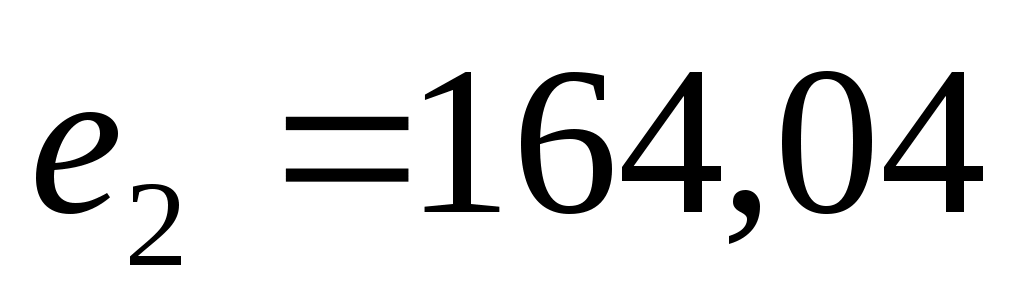 , , 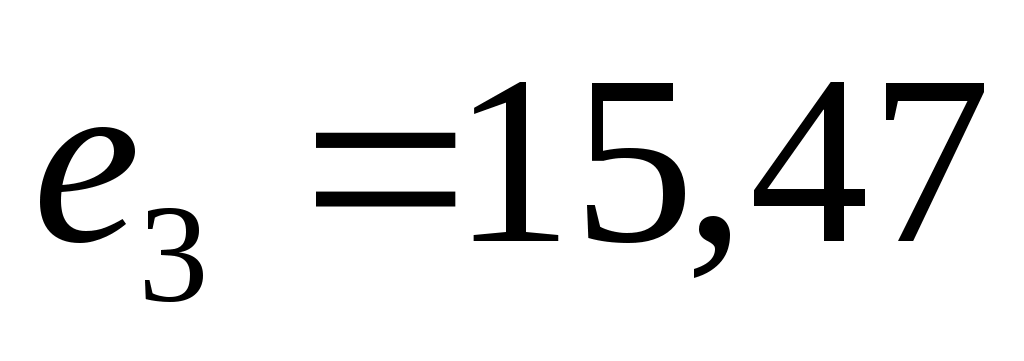 . Вектор решения равен {11,58; 0; 0; 23,51; 0; 9,30; 0; 0}. . Вектор решения равен {11,58; 0; 0; 23,51; 0; 9,30; 0; 0}.
Компромисс по принципу последовательной уступки. Предположили, что критерии ранжированы по важности в соответствии с их номерами. Нашли оптимальное решение по критерию 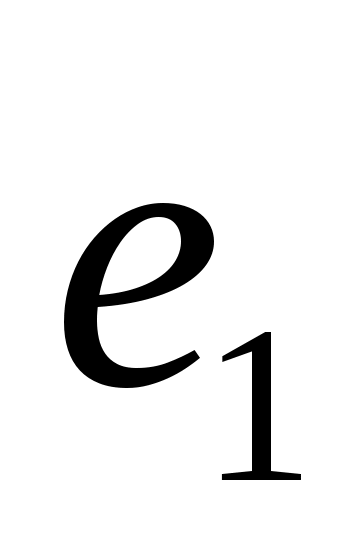 . Назначили уступку . Назначили уступку 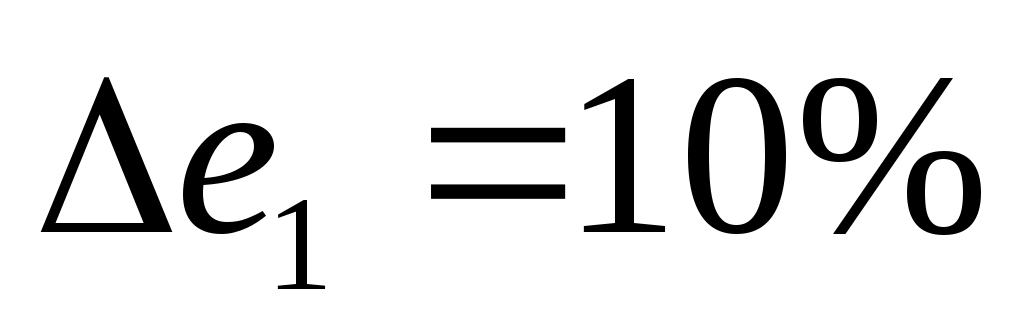 , которая вносится в качестве ограничения и позволяет максимизировать значение локального критерия , которая вносится в качестве ограничения и позволяет максимизировать значение локального критерия 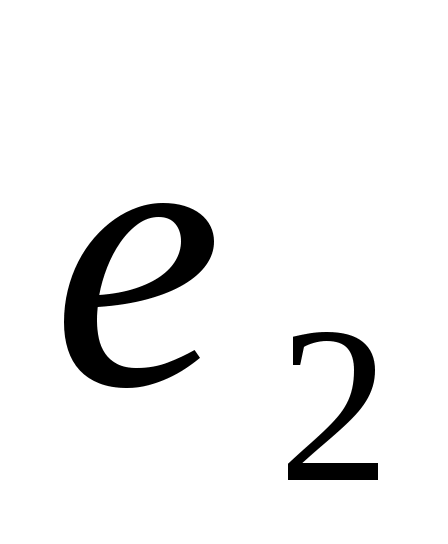 . Тогда . Тогда 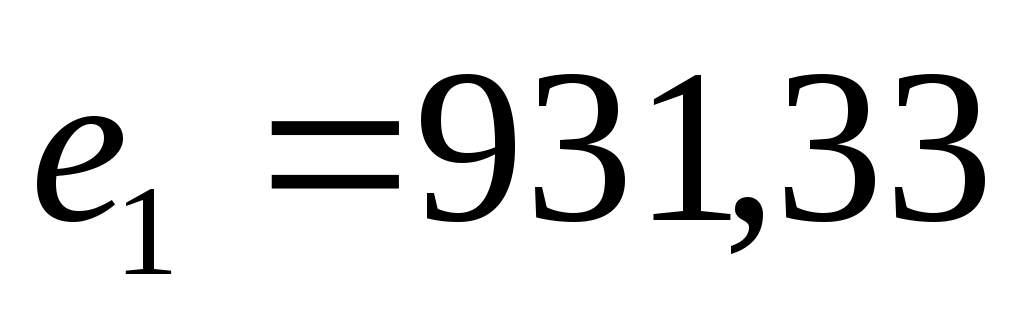 , а , а 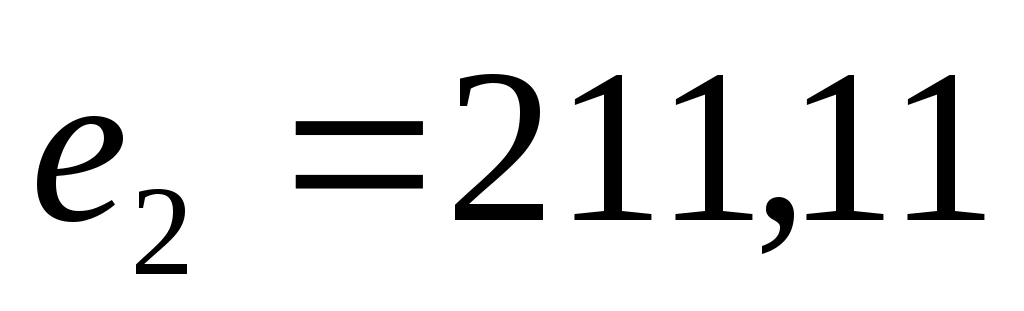 . Ввели уступку по второму критерию . Ввели уступку по второму критерию 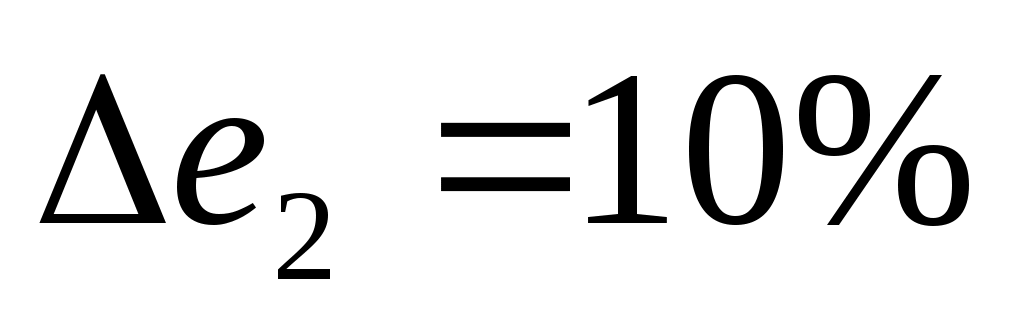 и максимизировали значение показателя и максимизировали значение показателя 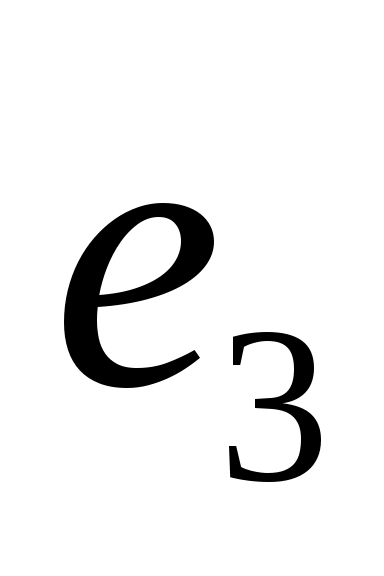 . Тогда . Тогда 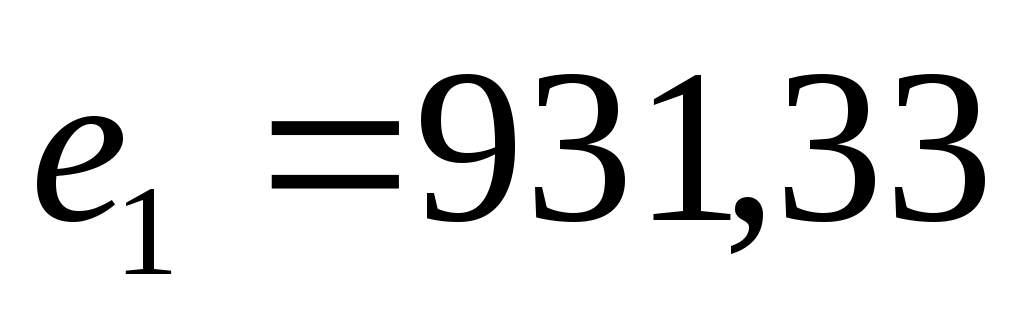 ; ; 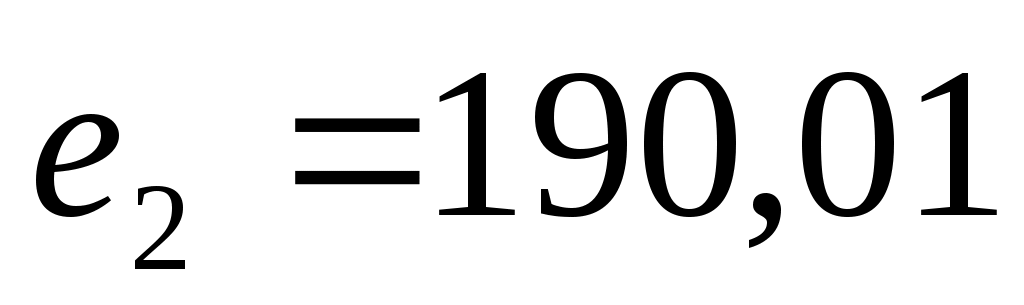 , а , а 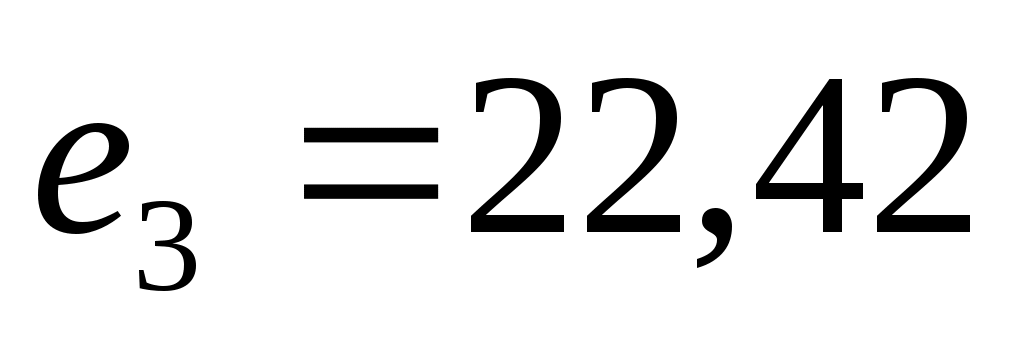 . Вектор решения имеет вид {0; 0; 0; 22,69; 0,01; 15,29; 0; 7,07}. . Вектор решения имеет вид {0; 0; 0; 22,69; 0,01; 15,29; 0; 7,07}.
Выводы:
Результаты решения многокритериальной задачи, полученные с помощью различных методов выбора компромисса, сведены в таблицу П33.
Таблица П33. Результаты решения многокритериальной задачи на основе различных принципов выбора компромисса
Метод
|
|
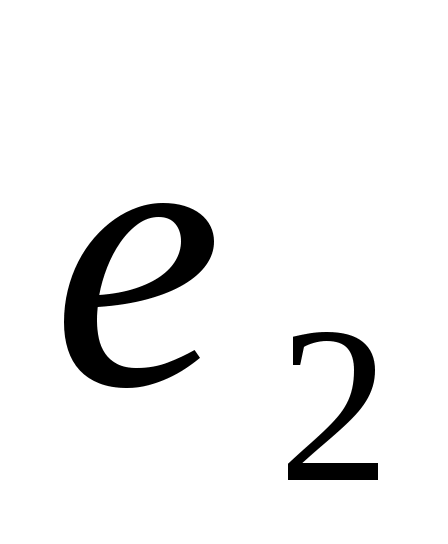
|
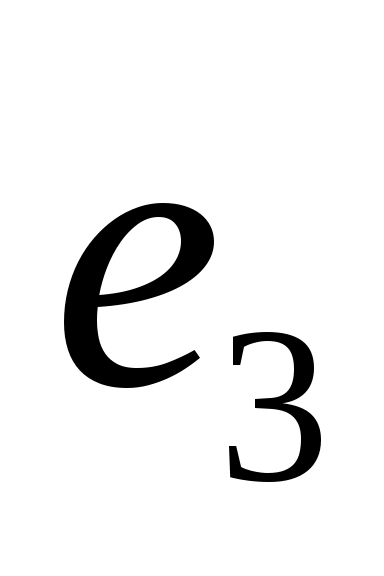
|
Решение
|
Скаляризации векторного критерия 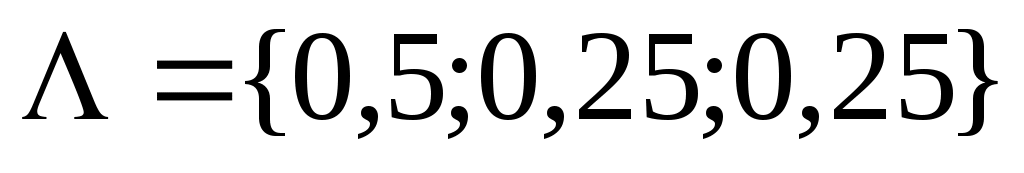
|
1018,41
|
123,59
|
12,36
|
{21,18; 0; 0; 19,61; 3,19; 0; 0; 0}
|
Скаляризации векторного критерия 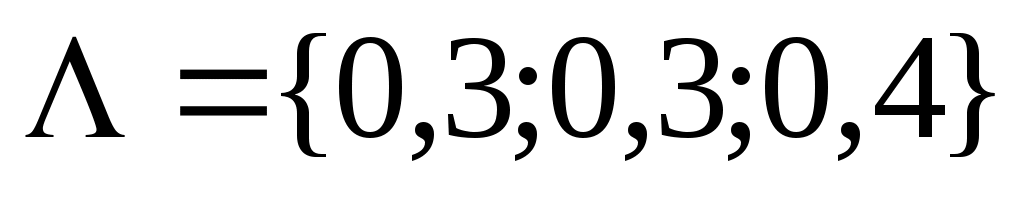
|
920,11
|
221,26
|
20,34
|
{0; 0; 0; 26,44; 0; 17,82; 0; 0}
|
Максимин
|
863,04
|
120,95
|
32,78
|
{0,00; 0,00; 0; 0,00; 15,12; 0; 0,00; 29,55}
|
Квазиравенство
|
1,09
|
0,09
|
0,09
|
{0; 0; 0,088889; 0; 0,011111; 0; 0; 0}
|
Принцип абсолютной уступки
|
983,33
|
164,04
|
15,47
|
{11,58; 0; 0; 23,51; 0; 9,30; 0; 0}
|
Принцип последовательной уступки
|
931,33
|
190,01
|
22,42
|
{0; 0; 0; 22,69; 0,01; 15,29; 0; 7,07}
| |
 Скачать 3.85 Mb.
Скачать 3.85 Mb.