Вороненко Соц медицина учебник. Социальная медицина как наука о здоровье общества и охране здоровья
 Скачать 5.8 Mb. Скачать 5.8 Mb.
|
|
Часть явления*100 Э  кстенсивный показатель = кстенсивный показатель = Целое явление Коэффициент определяется в процентах. Региональные экстенсивные показатели сравнивать нельзя. Это обусловлено тем, колебания остальных в определенном направлении (увеличении или уменьшении) может быть связано как сменою отображенной нами части явления, так и обратной сменою одной или нескольких других его частей. Так, уменьшение удельного веса может быть обусловлено увеличением другой части совокупности, притом, что целое остается неизменным (100%). Сравнение одних только экстенсивных показателей не позволяет определить, чем обусловлены данные изменения. Такая взаимосвязь является особенностью экстенсивных показателей. Например, удельный вес определенного заболевания в ее структуре может увеличиться: а) при приросте интенсивного коэффициента, если количество других заболеваний в этот период уменьшается; б) при снижении уровня данного заболевания, если уменьшение количества других заболеваний проходило быстрее. С помощью экстенсивных показателей нельзя делать вывод о расширении явления, однозначно правильным методом определения размеров частоты, уровня, расширения явления (заболеваемости, смертности и др.) в разных регионах является сравнение интенсивных показателей. Экстенсивные показатели имеют значения лишь для данного времени и места. Они довольно широко используются в практической деятельности с целью уяснения разделения конкретной совокупности на составные части. Показатель наличия отображает изменения, которые происходят с тем или иным явлением во времени, показывает их расхождения на отдельных территориях или в разных группах населения. Он показывает в сколько раз или на сколько процентов изменилось явление в динамике, или отличается по регионам не представляя при этом размеров остального. Для расчета показателя наличия одна из сравниваемых величин принимается за 1, 100 или 1000,а другие определяются в отношении к ней. Так, например, уровень смертности в районе А в прошлом году составлял 14,7 %о, а в текущем - 15,2 %о. Если показатель смертности за прошлый год принять за 100%, в текущем за Х, то результат будет равняться: 15,2 * 100  Х = =103,4 % Х = =103,4 % 14,7 Знаменатель отношения, то есть та величина, с которой другая подставлялась, называется основою или базой сравнения. В нашем примере основа - 14,7. Чтоб получить вывод, необходимо от определенной величины (Х) 103,4 % отнять предыдущий уровень, который брали за 100 %. 103,4 % - 100 % = 3,4 %. Вывод: уровень смертности в районе А увеличился на 3,4 %. При больших расхождениях (разностях) двух сравниваемых величин показатель наличия лучше показывать в кратности. Во сколько раз одна величина больше другой. Показатели наличия можно определить, используя абсолютные числа, показатели интенсивности, взаимоотношения или средней величины. Они используются для того, чтоб показать напрямик, тенденцию смены явления (увеличения или уменьшения), однако не раскрывают ни абсолютные размеры явления, ни его уровней. Показатели относительной интенсивности используются при изучении структурных особенностей различных статистических совокупностей, что имеют отношения к одной среде. Они являются численным взаимоотношением двух структур, Коэффициенты относительной интенсивности должны быть использованы только в тех случаях, когда отсутствует возможность определить прямые интенсивные коэффициенты. Эти показатели позволяют определить степень взаимоотношений (увеличения или уменьшения) аналогичных признаков. Например, удельный вес заболеваемости системы кровообращения в структуре первичных заболеваний устанавливается 15,2 %, в структуре инвалидности - 32,4 %, в структуре смертности - 59,2 %, Коэффициенты относительной интенсивности показывают, что заболевания системы кровообращения в 4 раза значительней, как причина смертности и в 2 раза, как причина инвалидности при установлении рангового места среди причин заболеваемости. Таким образом, коэффициенты относительной интенсивности являются фактически коэффициентами диспропорции удельного веса (значения) одноименных элементов в структуре разных процессов. Они не являются критерием частоты, а только мерой его сравнения. При анализе относительных величин иногда допускаются ошибки, к основным можно отнести:
3.4. Графическое изображение статистических данных Табличное объединение статистического материала часто требует наглядного изображения в виде графиков. График, в отличие от таблиц, более наглядно показывает общую картину распределения или тенденции развития явления. При его использование прослеживаются более выразительно взаимозависимости между показателями. Графики используются с целью облегчения восприятия материала, его статистического анализа, сравнения полученных данных. Они помогают лучше понять численные взаимоотношения признаков, закономерности и взаимосвязи отдельных явлений, сделать выводы наглядными. Графические изображения способствуют также популяризации и распространению статистических данных. Только правильно построенный график поможет проиллюстрировать выявленную закономерность или тенденцию. Графиком называется наглядное изображение статистических величин с помощью геометрических линий и фигур (диаграмм) или географических картосхем (картограмм). Каждый график, чтоб отвечать основным условиям использования, должны иметь следующие элементы: графический образ, поле, пространственные и масштабные ориентиры, масштабную шкалу, экспликацию. Графический образ - это геометрические знаки, линии, фигуры, с помощью которых изображаются статистические данные. Он должен отвечать цели и быть наиболее выразительным. Поле графика - это место размещения графических образов. Пространственные ориентиры - это система координатных сеток. Часто используют систему прямоугольных координат, кроме того, есть криволинейные шкалы. Они целесообразны в секторных диаграммах. Масштабом графика называется определенная мера перевода количественной величины в графическую. Масштабные ориентиры определяются системой масштабных шкал, которые бывают равномерными и неравномерными. При равномерных масштабных шкалах отрезки пропорциональны числам. Если, например, число удваивается, то отрезок между числами тоже должен быть в два раза больше. Экспликация - это название с коротким рассказом содержания, времени и места данных. На диаграмме также должны быть подписи вдоль масштабных шкал, пояснения и определенные элементы графика. По форме изображения диаграммы в свою очередь подразделяются на линейные, плоскостные, столбцовые, секторные, круговые, квадратные, фигурные, точечные, фоновые) и объемные. Линейные диаграммы используют для наглядного изображения процессов, которые показывают развитие явления во времени, его динамике, представленной в виде непрерывной линии при непрерывном процессе. Явление на такой диаграмме подается в виде линии, которая может быть прямою, ломаною, кривою (температурный лист больного, месячный вес ребенка, заболевания в зависимости от возраста и др.). При построении линейной диаграммы осью абсцисс является горизонтальная линия (ось Х), на ней откладывают отрезки для выбранных групп (например, по количеству годов, за которыми сравнивают данные). Они должны быть равны и непрерывны. Если статистические данные охватывают разные периоды времени, интервалы между периодами (длина отрезка) на оси абсцисс должны быть пропорциональны величинам длительности периодов. На вертикальной линии (ось У), ординаты, наносят риски, каждая из которых отвечает определенному количественному значению явления. Подсчет по масштабной линии проводится от базисной линии. После того, как на осях абсцисс и ординат нанесена шкала с установленным масштабом, соответственно приведенным данным, отмечают точки (координаты) на поле диаграммы, которые создаются пересечением двух прямых, проведенных перпендикулярно к соответствующим точкам на осях координат. Точки соединяются линиями. Пример линейной диаграммы приведен на рис.1. Нередко на одной линии диаграммы приводится несколько кривых, которые дают сравнительную характеристику динамики разных показателей или одного и того же показателя в разных регионах (например, смертность и рождаемость). Для того чтобы две линии отличались одна от другой, их нужно рисовать разным цветом или разными штрихами. Отдельный вид линейной диаграммы - радиальная диаграмма. Она создается в системе полярных координат и используется для изображения динамических данных, которые имеют циклическую закономерность. Например, частота вызовов скорой помощи к детям при заболеваниях пневмонией по месяцам года. Для создания такой диаграммы необходимо иметь соответствующее распределение вызовов. Радиусом любой величины описывают круг. Шестью диаметрами делят его на равные отрезки. Далее отмечают:
 Ежедневное число вызовов в каждом месяце * 100 Ежедневное число вызовов в каждом месяце * 100Ежедневное число вызовов в году На полученных таким образом двенадцати радиусах (по количеству месяцев), или их продолжениях, откладываем значение рассчитанного показателя пропорционально принятому масштабу. За масштаб выбирается величина радиуса, который отвечает ежедневному числу вызовов за год. Рассчитанные значения откладываются на принятой длине радиуса, и отмеченные точки соединяются линиями. Полученный многоугольник отображает колебание вызовов скорой помощи в каждом месяце в году. 1 2 12  100,0     3 11   138,0 134,0  100 4 9 5 6 8 7 Рис.2 . Месячные колебания вызовов скорой помощи к детям при заболеваниях пневмонией Среди плоскостных диаграмм расширенными являются столбцовые, внутренние столбцовые и секторные. Столбцовые диаграммы отображают абсолютные числа, интенсивные показатели (уровень заболеваемости, смертности, летальности), показатели взаимоотношения для одного или нескольких периодов, территорий, отдельных групп населения. При построении столбцевых диаграмм необходимо нарисовать систему прямоугольных координат, отметить размеры каждого столбца и интервала между ними. Основание столбцов, которые должны быть одинаковыми размерами, откладывается на оси абсцисс, а верхняя его часть будет отвечать величине показателя, нанесенный в соответствующем масштабе относительно оси ординат. Каждый отдельный столбец отвечает отдельному явлению или одному явлению за разные периоды времени. Расстояние между столбцами должно быть одинаковым, однако иногда они размещаются один около другого. Пример столбцовой диаграммы приведен на рисунке 3. 2  5 дни 5 дни19,6 18,9 16,3 15,9 13,8 12,4 2   0 0  1  5 5 1  0 05        0 0онкологические кардиологическое хирургическое повторное лечение терапевтическое инфекционное Рис. 3. Средняя продолжительность лечения взрослого населения в больницах различного профиля, Украина, 1997 год (койко-дни). Столбцовые диаграммы используются не только для сравнения явлений в динамике, а и для демонстрации состава определенного явления (внутренние столбцовые диаграммы). Внутренние столбцовые диаграммы используются для характеристики структуры определенного явления (смертности, заболеваний и др.), его составных частей. Составные части явления подаются в виде процентов от общего числа. При этом высота столбца берется за 100 % и делится на часть пропорционально удельному весу отдельных частей в процентах. Их располагают в порядке снижения (возрастания) процентов. Структуру исследуемого явления (заболеваемости, смертности и др.) можно показать также в виде секторной диаграммы (рис.4). 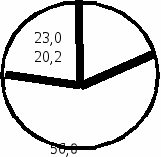 20,2 % - дети и подростки 56,8 % - население трудоспособного возраста 23,0 % - Население старше трудоспособного возраста Рис.4 Структура населения Украины по возрасту, 1998 год (%). Для построения секторной диаграмм радиусом произвольной величины описывают круг. На нем откладываются в градусах часть окружности, пропорционально процентному распределению изображения данных, которые определяются по формуле: Х = 360: 100 * а = 3,6 * а, Где Х - число градусов, а - число процентов. Размеченные отрезки круга соединяются линиями из центра, создавая сектора, которые наглядно демонстрируют структуру явления. Для большей наглядности используются объемные диаграммы, представляющие в виде геометрических фигур, рисунков, символов. Например, фигуры людей, рисунки кроватей - для изображения числа больных, кроватей и др. Картограммы и картодиаграммы дают представление о территориальном расширении определенного явления в абсолютных или относительных величинах, которые отмечаются на географических картах. Картограммы являются способом наглядного изображения практических показателей, которые характеризуют отдельные географические единицы (районы, области, государства) по тем или другим признака. Для этого на географическую карту наносят штрихованием или цветом разных оттенков различную интенсивности или распространение явления. Если взять для каждой группы районов определенный способ штрихования, то будет хорошо видно, как расположены на территории области разные районы с распространением заболеваний или других явлений (рис.5). Недочетом таких диаграмм является то, что они дают только общее представление об изменении статистических показателей в районах, а не показывают их абсолютные значения. Картодиаграмма отличается от картограмм тем, что на географическую карту определенной территории наносят в небольшом масштабе линейные, столбцовые диаграммы, которые отображают абсолютные или относительные числа. Это позволяет определить колебание показателей в регионах. При этом определенным цветовым фоном самой территории могут быть изображены другие показатели.
Любое статистическое исследование независимо от его объему, кроме оценки относительного уровня исследуемого явления или его структуры, завершается расчетом и оценкой обобщающих статистических критериев. Наиболее распространенной формой статистических показателей являются средние величины, которые дают обобщенную количественную характеристику определенного признака в статистической совокупности в определенных условиях места и времени. Они отображают типичные черты вариационных признаков исследуемых явлений. Основываясь на том, что количественная характеристика признака связана с ее качественной стороной, среднюю величину следует рассматривать в мировых условиях качественного анализа. Кроме обобщающей оценки определенного признака определение средних для совокупности непостоянных количественных величин возникает также тогда, когда сравнивают две их качественно отличных друг от друга группы. В практике охраны здоровья средние величины используются достаточно широко:
С помощью средних можно сравнивать между собой совокупности, которые имеют разные вариабельность признаков. Средние характеристик широко используются для сравнения во времени, что позволяет характеризовать наиважнейшие закономерности развития явления, Так, например, закономерность увеличения роста детей определенного возраста находит свое отражение в обобщающих показателях физического развития. Закономерности динамики (увеличения или уменьшения) частоты пульса, дыхания, клинических параметров при определенных заболеваниях находят свое проявление в статистических показателях, которые отображают физиологические параметры организма и др. При этом в отдельных индивидуальных случаях данная тенденция не всегда будет определяться. Например, при лабораторных исследованиях диагностируется общее увеличение числа лейкоцитов, которое выявляют у определенных лиц под влиянием тех или иных причин (радиационное загрязнение территории). В разные годы уровень данного параметра может не увеличиваться, проявляться не одинаково в регионах вследствие разных конкретных условий. В связи с этим очень важно, чтоб средние показатели были обоснованы на массовом обобщении фактов. Это позволяет выявить общую тенденцию и показать типичный для данного периода времени и региона уровень явления. В такой ситуации средние величины не учитывают случайные отклонения индивидуальных величин от общей тенденции, которые присущи генеральной совокупности. В этом проявляется действия закона больших чисел. Чаше при изучении медико-биологических данных используется:
Кроме того, практическое использование находят обобщающие описательные (непараметрические) характеристики вариативных признаков - мода и медиана. Средние величины должны определятся на основе массового обобщения фактов, и применяться для качественно однородных совокупностей - это основное условие их практического и научного использования. Средние величины нельзя определить, если совокупность исследуемых признаков, процессов, явлений складывается из неоднородных элементов. Обоснованность научно-практического значения средних величин имеет место только при условии правильного группирования. Основными способами при расчете средней величины является качественно однородная совокупность и достаточное число наблюдений. Качественно однородная совокупность означает, что все ее единицы принадлежат к одному виду явлений. Например, число дней нетрудоспособности больных по определенной нозологической форме, масса детей - мальчиков 7 лет; пульс детей одного года при определенных заболеваниях и др. Смешивание совокупностей, которые определяются разными качественными признаками, приводит для расчета нетипичных средних величин. Таким образом, средние величины в статистике только тогда могут быть основой научного анализа, когда отображают качественно однородную совокупность. Качественная однородность явлений, их типичность, базируется на основе теоретического анализа их сущности. Обязательным условием, которому должен отвечать настоящий статистический материал для расчета средних величин, является также достаточное число наблюдений. Данный критерий можно определить с помощью формул, которые представлены в разделе "Организация и проведение статистического исследования". Отдельные элементы (значения) совокупности однородных по качественному составу предметов, явлений, параметров являются вариантами, а всю совокупность можно представить в виде вариационного ряда, который является основой для определения средних величин. Вариационный ряд - это ряд вариантов и отвечающих им частот. Вариационные ряды дают возможность установить характер распределения единиц совокупности по тем или иным количественным признаком и ее вариацию - разносторонность индивидуальных значений признаков конкретных единиц совокупности. Отдельные значения вариантов определенного признака обозначаются буквой Х. Число, которое показывает, как часто встречается тот или иной вариант в составе данного ряда, называется частотой (f), Сумма частот (∑ f) равна общему числу наблюдений (n). Вариационный ряд может быть простым, где каждый вариант представлен отдельно, поэтому частота каждого из них равна единице, Например, распределение больных по частоте пульса: 68, 69, 75,70, 65, 688, 70, 75, 74, 72, 72, 68. Данный ряд является не ранговым, потому, что варианты не систематизированы. Систематизируя варианты в порядке увеличения или уменьшения их числовых значений, данный ряд можно переделать в ранговый: 65, 68, 68, 68, 69, 70, 70, 72, 72, 74, 75, 75. Если варианты сгруппировать по их абсолютной величине, то можно получить сгруппированный вариационный ряд, где каждый вариант представлен со своей частотой. Для нашего примера: X  65 68 69 70 72 74 75 65 68 69 70 72 74 75 |
