Лекции по ОПМ. Тема 1 Структурная реформа железноднорожного транспорта
 Скачать 1.15 Mb.
|
|
Тема 3. СЕТЕВЫЕ МЕТОДЫ ПЛАНИРОВАНИЯ И УПРАВЛЕНИЯ (СПУ) 3.1 Основные понятия и элементы сетевого графика Основным плановым документом в системе СПУ является сетевой график, представляющий собой информационно-динамическую модель, в которой изображаются взаимосвязи и результаты всех работ, необходимых для достижения конечной цели разработки. В сетевом графике детально или укрупненно показывается, что, в какой последовательности, за какое время надо выполнить, чтобы обеспечить окончание всех работ не позже заданного (директивного) срока. В основе построения сетевого графика лежат следующие основные понятия: работа, зависимость, событие, путь. Работой называют любой трудовой процесс (или их совокупность), связанный с затратами времени и ресурсов. В понятие работа входит также и ожидание, т.е. пассивный процесс, не требующий затрат труда и материальных ресурсов, но отнимающий время. К таким процессам относятся естественная сушка после окраски оборудования, процесс зарядки аккумуляторов, затвердевание бетона и т.п. Зависимость (фиктивная работа) представляет собой технологическую или организационную связь между работами и, естественно, не требует ни времени, ни ресурсов. Событие - результат выполнения одной или нескольких работ, предоставляющий возможность начать последующие работы. Путь - это любая последовательность работ, в которой конечное событие каждой работы совпадает с начальным событием следующей за ней работы. 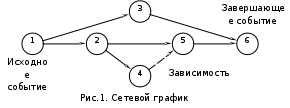 На сетевом графике события изображаются кружками с порядковым номером, действительные работы – сплошными, фиктивные работы - пунктирными стрелками. На рис. 1 даны элементы сетевого графика. Все работы, входящие в сетевой график, имеют временные оценки, измеряются в часах, днях, месяцах и т.п.; продолжительность работ пишут под стрелками. Путь от исходного до завершающего события называют полным. В любом сетевом графике возможно большое количество таких путей. График на рис. 1 содержит четыре полных пути: 1-3-6; 1-2-3-6; 1-2-5-6; 1-2-4-5-6. Полный путь максимальной продолжительности называют критическим. Продолжительность (длина) критического пути определяет длительность всей разработки. В сетевом графике может быть один или несколько критических путей. Степень сложности сетевого графика характеризуют с помощью коэффициента сложности. Коэффициент сложности представляет собой отношение суммы числа работ и зависимостей к числу событий. При значении коэффициента менее 1,2 график считают простым, от 1,2 до 1,5 - средней сложности и более 1,5 - сложным. 3.2 Правила построения сетевых графиков При построении сетевых графиков должны быть учтены следующие правила: Каждая работа должна быть заключена между двумя событиями. При этом нельзя допускать различных работ, имеющих одинаковые коды, т.е. работ с общим начальным и конечным событиями (рис.2,а). В подобных случаях в сеть необходимо ввести промежуточное событие и фиктивную работу так, как это показано на рис.2,б. 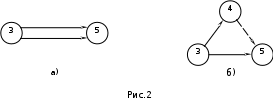 В сети не должно быть «тупиковых» событий, например, событие 3 на рисунке 3, т.е. событий, от которых не начинается ни одна работа. Исключение составляет завершающее событие всего комплекса работ. Наличие в сети таких тупиков показывает, что или допущена явная ошибка при построении сети, или данное событие, а, следовательно, и предшествующие ему работы никому не нужны и никак не влияют на выполнение конечной цели - свершение завершающего события сети. 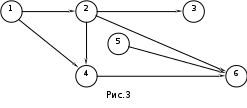 В сети не должно быть также так называемых "хвостовых" событий (событие 5 на рис.3), т.е. событий, которым не предшествует ни одна работа, за исключением, конечно, исходного события сети. Выявленные "хвостовые" события говорят нам или о том, что совершена случайная ошибка при построении сетевой модели, или о том, что работы, которые должны быть выполнены для свершения данного события, не имеют исполнителей. Необходимо проверить сеть на наличие в ней "замкнутых контуров" (циклов), т.е. путей, "которые соединяют начальное событие с ним же самим (путь 4-6-5-4 на рис.4). Это легко выявить по направлению стрелок, показывающих последовательность выполнения работ. В этом случае направление стрелок приводит нас опять к событию, от которого была начата проверка. 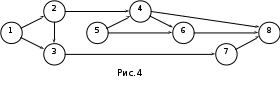 Сеть должна иметь наглядный, простой вид, легко обозримый, и давать возможность быстро по ней ориентироваться. Предварительно составленную сеть целесообразно перестроить так, чтобы обеспечить минимальное количество пересечений одних работ другими, так как всякие пересечения очень затрудняют чтение сетевого графика. На рисунке 5 показан пример такой перестройки сети: на рис.5,а – нерекомендуемый способ начертания сети, а на рис.5,б и 5,в – рекомендуемый. 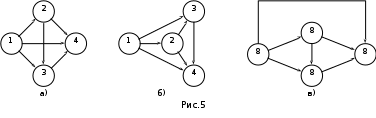 Задача 3 Необходимо провести следующий комплекс работ (см. рис.6): механическую обработку деталей Х (работа 1-2) и Y (работа 2-3) на токарном станке, термообработку деталей Х (работа 3-4), зачистку заусенцев на деталях Y (работа 3-5). Какова ошибка в изображении этой зависимости? 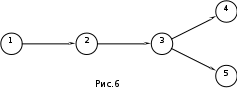 Задача 4 Определите ошибки, допущенные при построении сетевых графиков на рис.7,8,9. 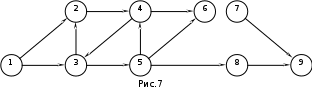 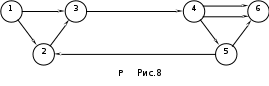 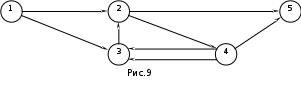 Задача 5 Преобразуйте сети, приведенные на рис.10,11,12, максимально сократив число пересечений работ. 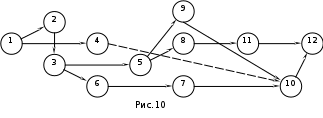 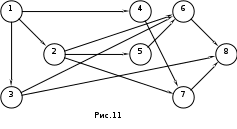 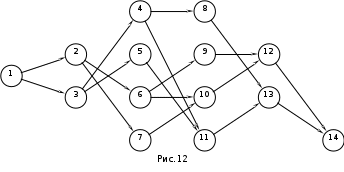 Задача 6 Вычислите коэффициенты сложности графиков, показанных на рис.8,11,12. Назовите, к каким категориям сетевых графиков они относятся: простым, средней сложности или сложным. 3.3 Параметры сетевых графиков и методы их расчета Чтобы получить показатели, необходимые для планирования и управления, рассчитывают следующие параметры сетевого графика: продолжительность критического пути Ткри работ, лежащих на нем; р  аннее начало  и раннее окончание  каждой работы;позднее начало  и позднее окончание  каждой работы;резервы времени по работам: полный  и свободный  .Величина промежутка времени между моментами начала и окончания работы называется ее продолжительностью (tij). Обычно очередность расчетов принимают в таком порядке: определяют ранние сроки начала и окончания всех работ, начиная от исходного события и кончая завершающим; на основе вычисленных ранних сроков устанавливают критический путь и его продолжительность, затем определяют поздние сроки начала и окончания, после чего вычисляют полные и свободные резервы времени работ. Кроме временных параметров работ могут быть вычислены параметры событий, ранние и поздние сроки наступления событий и резерв времени (Ri), Ранний срок наступления события  - минимальный из возможных моментов наступления данного события при заданных продолжительностях работ и начальном моменте. Эта величина определяется суммарной продолжительностью всех работ, лежащих на самом длинном пути от начального события до данного.Поздний срок наступления события  - максимальный из допустимых моментов наступления данного события, при котором еще возможно выполнение всех следующих работ с соблюдением директивного срока наступления завершающего события Тдир. Директивный срок Тдирможет совпадать или превышать продолжительность критического пути, т.е. Тдир ≥ Ткр. Поздний срок наступления события определяется как разница между директивным сроком наступления завершающего события Тдири наибольшей продолжительностью пути от завершающего события графика до рассматриваемого. Превышение вызовет аналогичную задержку наступления завершающего события.Ранний срок начала (окончания ) работы - это минимальный из возможных моментов начала (окончания) данной работы при заданных продолжительностях работ и заданном начальном моменте: ; .Наибольшая величина из ранних окончаний завершающих работ графика - это длина максимального пути от исходного до завершающего события графика, т.е. критического пути.  .Поздний срок начала (окончания ) работы - это максимальный из допустимых моментов начала (окончания) данной работы, при которых еще возможно выполнение всех следующих работ с соблюдением директивного срока наступления завершающего события. Очевидно: ; .Поздние сроки начала и окончания работ определяются обратным ходом от завершающего события к исходному, т.е. справа налево. Позднее окончание завершающих работ всегда равно длине критического пути (или Тдир, если Тдир > Ткр). Резерв времени события Ri - это максимальный промежуток времени, на который может быть отсрочено совершение этого события без нарушения сроков завершения разработки в целом.  .Резервами времени располагают не только события, но и работы. Различают полный и свободный (частный) резервы времени работы. Полный резерв времени работы - максимальное время, на которое можно отсрочить начало или увеличить продолжительность работы, не изменяя директивного срока наступления завершающего события. .В случае, когда Тдир = Ткр, работы, лежащие на критическом пути, полного резерва времени не имеют, их ранние параметры совпадают с поздними. У отдельных работ помимо полного резерва времени имеется свободный резерв времени  . Свободный (частный) резерв времени работы - это максимальное время, на которое можно отсрочить начало или увеличить продолжительность работы, при условии, что все события сети наступают в свои ранние сроки,  .Свободный резерв времени критических операций равен нулю, так как в отношении этих операций не может быть допущена никакая отсрочка в начале их выполнения. Задача 7 Вычертить сетевой график на строительство и монтаж участка ЛЭП-110 кВ по заданному перечню и кодам работ (табл.1).Определить коэффициент сложности построенной сетевой модели. Таблица 1
Задача 8 Рассчитать временные параметры сетевого графика установки опор и конструкций контактной сети на перегоне двухпутного участка. Сетевой график приведен на рис.13 показатели отдельных работ приведены в табл.2. 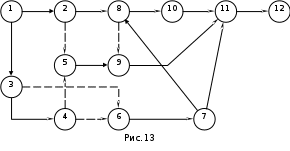 Результаты расчета, представить в форме, показанной в табл.3. Таблица 2
Таблица 3
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
