конспект теормех. теоретическая механика
 Скачать 3.7 Mb.
|
РАВНВЕСИЕ ТЕЛ ПРИНАЛИЧИИ СИЛ ТРЕНИЯТрение скольженияОпыт показывает, что при стремлении двигать одно тело по поверхности другого в плоскости соприкосновения тел возникает сила сопротивления их относительному скольжению. Эту силу, называют силой трения скольжения. Р  Рис.1.17 азложим силу реакции  шероховатой поверхности на составляющие: одну из которых  направим по общей нормали к поверхности соприкосновения, а другую  направим в касательной плоскости к этим поверхностям (сила трения).Силой трения скольжения (или просто силой трения) называется составляющая силы реакции связи, которая лежит в касательной плоскости к поверхностям соприкасающихся тел (рис.). Силой нормальной реакцией связи называется составляющая силы реакции связи, которая направлена по общей нормали к поверхностям соприкасающихся тел.  Сухим трением называется трение, когда между поверхностями соприкасающихся тел нет смазывающего вещества. Законы Кулона Сила трения скольжения находится в общей касательной плоскости соприкасающихся поверхностей тел и направлена в сторону, противоположную направлению возможного скольжения тела под действием активных сил. Сила трения зависит от активных сил, и её модуль заключён между нулём и максимальным значением, которое достигается в момент выхода тела из положения равновесия, то есть:   - называется предельной силой трения.Предельная сила трения скольжения при прочих равных условиях не зависит от площади соприкосновения трущихся поверхностей. Из этого закона следует, что для того чтобы сдвинуть, например кирпич, надо приложить одну и туже, силу, независимо, от того, какой гранью он положен на поверхность, широкой или узкой. Предельная сила трения скольжения пропорциональна нормальной реакции (нормальному давлению):  ,где безразмерный коэффициент  н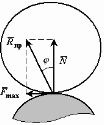азывают коэффициентом трения скольжения; он не зависит от нормальной реакции.К  Рис. 1.18 оэффициент трения скольжения зависит от материала и физического состояния трущихся поверхностей, то есть от величины и характера шероховатости, влажности, температуры и других условий. Коэффициент трения устанавливается экспериментально. Считается, что коэффициент трения не зависит от скорости движения. Угол трения. Условия равновесия Многие задачи на равновесие тела на шероховатой поверхности, т.е. при наличии трения, удобно решать геометрически. Для этого введем понятие угла и конуса трения. Реакция реальной (шероховатой) связи  слагается из двух составляющих: нормальной реакции  и перпендикулярной ей силы трения  . Следовательно, реакция связи отклоняется от нормали к поверхности на некоторый угол. При изменении силы трения от нуля до максимальной, сила реакции меняется от нуля до  , а ее угол с нормалью растет от нуля до некоторого предельного значения .Углом трения называется наибольший угол  м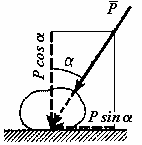ежду предельной силой реакции шероховатой связи и нормальной реакцией . ;  ;.У  Рис.1.19 гол трения  зависит от коэффициента трения.Конусом трения называют конус, описанный предельной силой реакции шероховатой связи  вокруг направления нормальной реакции.Если к телу, лежащему на шероховатой поверхности, приложить силу Р, образующую угол  с нормалью, то тело сдвинется только тогда, когда сдвигающее усилие  будет больше предельной силы трения  (если пренебречь весом тела, то  но неравенство  Выполняется только при  , т.е. при  ,Следовательно, ни какой силой, образующей с нормалью угол , меньший угла трения тело вдоль данной поверхности сдвинуть нельзя.Для равновесия твёрдого тела на шероховатой поверхности необходимо и достаточно, чтобы линия действия равнодействующей активных сил, действующих на твёрдое тело, проходила внутри конуса трения или по его образующей через его вершину. Тело нельзя вывести из равновесия любой по модулю активной силой, если её линия действия проходит внутри конуса трения. Пример. Рассмотрим тело имеющее вертикальную плоскость симметрии. Сечение тела этой плоскости имеет форму прямоугольника. Ширина тела равна 2a. К телу в точке С, лежащей на оси симметрии, приложена вертикальная сила  и 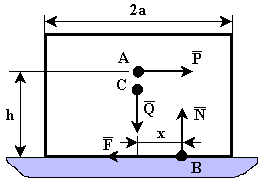в точке А, лежащей на расстоянии h от основания, горизонтальная сила  . Реакция плоскости основания (реакция связи) приводится к нормальной реакции и силе трения . Линия действия силы неизвестна. Расстояние от точки С до линии действия силы обозначим x. ( ). Составим три уравнения Р  ис.1.20 равновесия:    Согласно закону Кулона  ,  . Так как  , то  Возможны варианты. Если  , то равновесие будет иметь место до тех пор, пока сила трения не достигнет своей предельной величины, условие (1) превратится в равенство. Дальнейшее увеличение силы приведет к скольжению тела по поверхности.Если  , то равновесие будет иметь место до тех пор, пока сила трения не достигнет величины  , условие (2) превратится в равенство. Величина x будет равна h. Дальнейшее увеличение силы приведет к тому, что тело станет опрокидываться вокруг точки B (скольжения не будет).Трение качения Трением качения называется сопротивление, возникающее при качении одного тела по поверхности другого. Установлены следующие приближенные законы для наибольшего момента пары сил, препятствующих качению. 1.Наибольший момент пары сил, препятствующих качению, в довольно широких пределах не зависит от радиуса катка. 2. Предельное значение момента  пропорционально нормальной реакции  . .Коэффициент пропорциональности k называют коэффициентом трения качения при покое. Размерность k - это размерность длины. 3.Коэффициент трения качения k зависит от материала катка, плоскости и физического состояния их поверхностей. Коэффициент трения качения при качении в первом приближении можно считать не зависящим от угловой скорости качения катка и его скорости скольжения по плоскости. Рассмотрим движение ведомого колеса. Для вагонного колеса по рельсу  мм.Качение колеса начнется, когда выполнится условие  или  .Скольжение колеса начнется, когда выполнится условие  .Обычно отношение  и качение начинается раньше скольжения.Если  , то колесо будет скользить по поверхности, без качения.ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ. Сложение двух параллельных сил Равнодействующая двух параллельных сил имеет тоже направление; её модуль равен сумме величин составляющих сил; точка приложения равнодействующей лежит внутри отрезка АВ и удовлетворяет правилу обратной пропорциональности плеч. Равнодействующая двух антипараллельных сил имеет направление большей силы; её модуль равен модулю разности величин составляющих сил; точка приложения равнодействующей лежит вне отрезка АВ со стороны большей силы и удовлетворяет правилу обратной пропорциональности плеч. Пусть к твердому телу приложена система параллельных сил, можем тогда отыскивать их равнодействующую 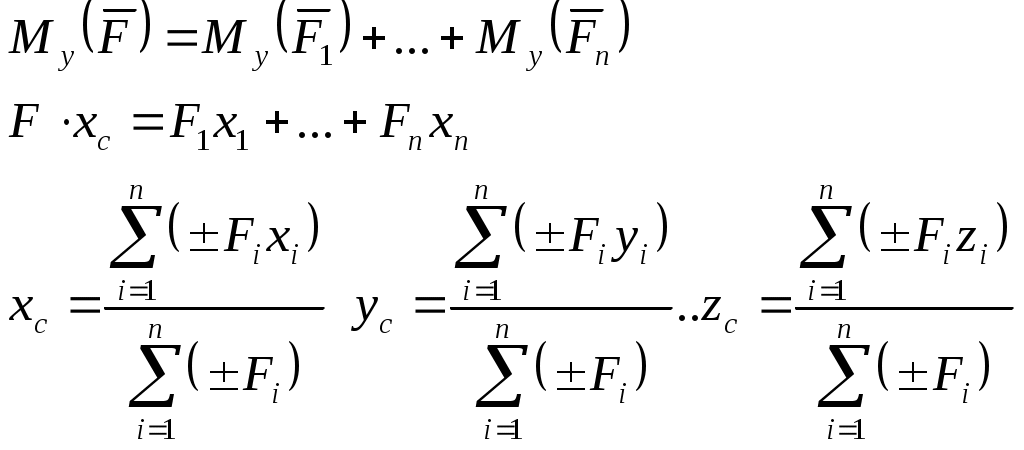 , пользуясь правилом сложения двух сил. Суммируя последовательно силы придем к равнодействующей , приложенной к точке  . Такая точка называется центром параллельных сил. Координаты центра параллельных сил вычисляются путем составления равенства моментов относительно координатных осей (например, y) ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА. В 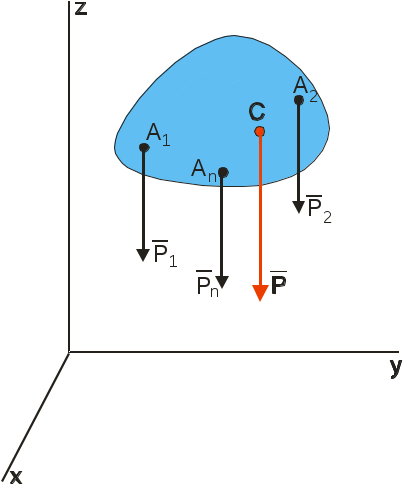 Рис. 1.21 ес тела  находящегося вблизи земли – это равнодействующая всех сил тяжести  действующих на малые частицы тела  :Если размеры тела малы по сравнению с землей, то все силы тяжести 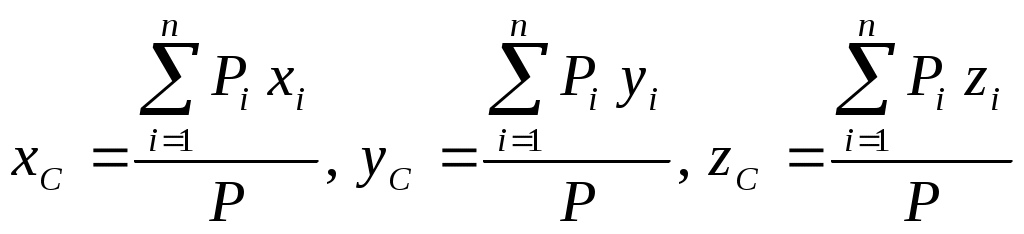частиц тела можно считать параллельными и для определения положения точки , к которой приложен вес тела (это центр тяжести тела), можно воспользоваться предыдущими формулами для координат центра параллельных сил. В них все силы берем со знаком плюс и знаменатель  . Эти формулы примут вид: (1).Для тела произвольной формы суммирование следует заменять интегрированием по всему телу. Рассмотрим частные случаи применения этих формул. Центр тяжести объема: Это центр тяжести однородного тела заполняющего данный объем V. Пусть плотность такого тела  , тогда в (1) веса  , где  - объем  -той частицы. . (2)Центр тяжести площади: Это центр тяжести однородной тонкой пластины, имеющей очертание данной плоской фигуры с площадью S, h – толщина однородной тонкой пластины. Из (2):  ,    .3) Центром тяжести линии называется центр тяжести однородной тонкой проволоки, ось которой совпадает с данной линией. Центр тяжести линии длинны L вычисляется по формулам: 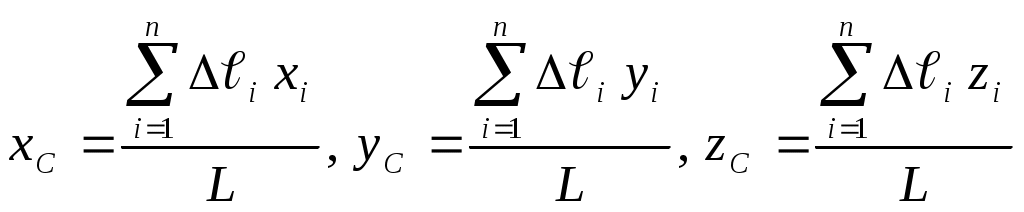 .Некоторые приемы определения центра тяжести Если тело имеет плоскость или ось симметрии, то центр тяжести лежит на этой плоскости или оси. Формулы (1) – (3) можно использовать разбивая тело на конечное число частей простой формы. Координаты центров которых известны. Метод отрицательных объемов и площадей. Этот метод используется для тел с выемками. При этом тело рассматривают состоящим из двух частей: Одна – это сплошное тело, вторая – выемка, которой приписывают отрицательный объем или площадь. |