конспект теормех. теоретическая механика

• Название: теоретическая механика
• Анкор: конспект теормех
• Дата: 03.04.2022
• Размер: 3.7 Mb.
• Имя файла: Konspekt-1_Teor_Mekh.doc
• Тип: Протокол; #437783
• страница: 6 из 7

ЧАСТНЫЕ СЛУЧАИ ДВИЖЕНИЯ ТОЧКИ

1. 
   Равномерное движение. Это движение, при котором скорость точки постоянна по величине, V=const.
   

Траектория точки при этом может быть криволинейной. Касательное ускорение , т.е. при равномерном движении полное ускорение состоит только из нормального .

2. 
   Прямолинейное движение (не обязательно равномерное).
   

Для прямолинейной траектории радиус кривизны , тогда , т.е. в этом случае полное ускорение, наоборот, состоит из касательного

3. 
   Равномерное движение – движение с постоянным по величине и знаку касательным ускорением, . Обычно этот случай разделяют на два: равноускоренное движение, когда , и равнозамедленное . В обоих случаях справедливы равенства:
   

, ,V₀ – начальная скорость;

-, т.е. при равнопеременном движении скорость изменяется по линейному закону, а криволинейная координата по квадратичному во времени.
ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА

Существует пять видов движения твердого тела:

1. 
   поступательное движение;
   
2. 
   вращение вокруг неподвижной оси;
   
3. 
   плоское движение;
   
4. 
   вращение вокруг неподвижной точки;
   
5. 
   свободное движение.
   

Первые два называются простейшими движениями твердого тела.
ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА И ЕГО СВОЙСТВА.

Поступательное движение – движение, при котором любая прямая, проведенная в нем, остается параллельна самой себе.

Примеры: движение кузова автомобиля на прямолинейной дороге (в этом случае траектории всех точек кузова – это параллельные прямые); круговое поступательное движение:

П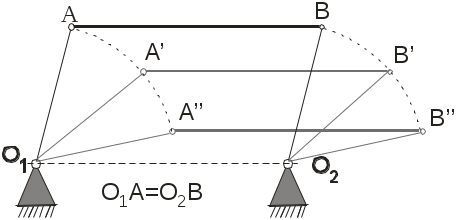


Рис.1.28
римером поступательного движения может служить движение спарника (рис.) – стержня шарнирно закрепленного на двух кривошипах.

Если длины кривошипов равны О₁А=О₂В, то спарник АВ совершает поступательное круговое движение, т.е. все его точки движутся по окружностям одинаковых радиусов, но со сдвинутыми центрами.

Вообще траекториями точек тела при поступательном движении могут быть любые кривые.

Теорема: при поступательном движении тела траектории всех его точек равны, т.е. при наложении совпадают, а скорости и ускорения векторно равны: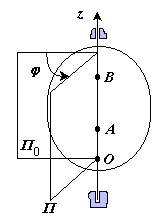




Рис.1.29
, .

Из теоремы видно, что все точки тела при поступательном движении движутся одинаково. Таким образом, при поступательном движении можно говорить о скорости, ускорении и траектории такого движения, приписывая их к любой точки тела.
ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ. УГЛОВАЯ СКОРОСТЬ И УГЛОВОЕ УСКОРЕНИЕ.
При таком вращении точки тела, лежащие на оси, остаются неподвижными, а любая точка М, отстающая от оси на расстоянии ОМ=h, будет совершать движение по окружности радиуса h с центром на оси. Плоскости таких окружностей перпендикулярны оси.

Для того, чтобы задать вращательное движение достаточно для любой точки М тела, не лежащей на оси задать угол , где М₀ – положение этой точки в начальный момент времени t₀=0. Угол φ в радианах называется угловой координатой тела, а уравнение (1) называется уравнением или законом вращения. Положительное направление отсчета φ принимают против часовой стрелки, если смотреть с положительного направления оси z. Основными кинематическими характеристиками вращательного движения являются его угловая скорость и угловое ускорение тела.

Угловая скорость определяет изменение угла φ во времени. Угловая скорость определяется формулой:

или .

Таким образом, мгновенная угловая скорость – есть производная угловой координаты по времени ([]=рад/с=с^-1).

В технике часто для измерения угловых скоростей многооборотных вращений (турбин, валов и т.д.) применяют внесистемную единицу измерения угловых скоростей [n]=об/мин



Угловое ускорение характеризует изменение угловой скорости во времени:

или ,

Таким образом, угловое ускорение в данный момент есть производная от угловой скорости по времени. Учитывая определение , получим . Таким образом, угловое ускорение - вторая производная от угловой координаты по времени ([ε]=рад/с²=с^-2). Вращение будет ускоренным (т.е. величина  возрастает), если  и ε одинаковых знаков, и замедленным, если они разных знаков.

В кинематике часто используют векторные представления угловой скорости и углового ускорения, т.е. считают, что , г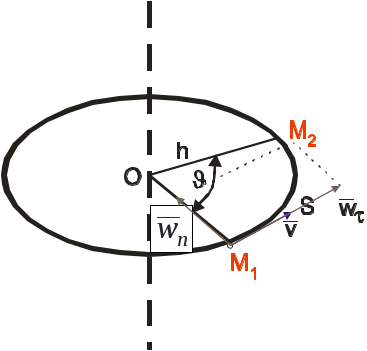де - орт оси z. Причем вектор отсчитывают от любой точки на оси. Угловое ускорение считают также вектором или . Вектор направлен в сторону , если вращение ускоренное, и в противоположную сторону, если замедленное.

У


Рис.1.30
гловые скорость и ускорение характеристики вращательного движения твердого тела как целого. В тоже время каждая его точка в отдельности обладает линейными скоростью и ускорением. Поскольку траектория точки М во вращательном движении известно - это дуга окружности радиуса ОМ=h, для то определения скорости и ускорений удобно использовать естественная способ задания движения, принимая в качестве криволинейной координаты длину дуги окружности ММ .

Тогда: =





Таким образом, величина скорости во вращательном движении есть произведение расстояния h на угловую скорость тела.

Вектор точки М направлен по касательной к окружности радиуса ОМ, т.е. ортогонально этому радиусу.

Касательное ускорение по величине будет: , .

Касательное ускорение равно произведению расстояния h на угловое ускорение тела.

В первом случае вектор направлен в сторону скорости, во втором – в противоположную. Для определения величины нормального ускорения так же применим общую формулу нормального ускорения из кинематики точки:

,

Таким образом, нормальное ускорение по величине не есть произведение расстояния h на квадрат угловой скорости. Полное ускорение:


Таким образом, что, зная и , можно полностью определить векторы

Замечание: поскольку и также пропорциональны h, то получаем аналогичное правило для определения эпюры ускорений.

Все векторы ускорений точек на радиусе OM параллельны , т.е. ускорению точек на ободе диска.
Частные случаи вращательного движения.

1) Равномерное вращение – вращение с постоянной угловой скоростью.

.

При равномерном вращении угол поворота линейно возрастает во времени.

2)Равнопеременное вращение – вращение с постоянным угловым ускорением. Так же как и в случае равнопеременного движения точки здесь выделяют равноускоренное вращение (E>0) и равнозамедленное (E<0)
здесь: - начальная угловая скорость.



Пример:

Дано:

,

Найти:

(полное число оборотов)

Решение:



Случай равноускоренного вращения.

,


ФОРМУЛЫ РИВАЛЬСА (ВЕКТОРНЫЕ ФОРМУЛЫ СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ВРАЩАЮЩЕГОСЯ ТЕЛА).

Будем определять вектор точки вращающегося тела, угловая скорость которого. Вектор точки, отсчитываемый от начала . Покажем, что для скорости точки справедливо векторное равенство:

(1)

По определению векторного приведения величина его здесь будет 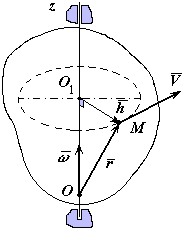. Здесь, как следует из , . По направлению векторное произведение должно быть направлено перпендикулярно плоскости в ту сторону, откуда поворот вектора к вектору на наименьший угол виден против часовой стрелки. Все то же самое можно сказать и о направлении вектора . Для полного ускорения точки продифференцируем (1) по времени используя правило дифференцирования векторных произведений:




Рис.1.31
,

В результате приходим к равенству: (формула Ривальса).

Можно доказать, что первое векторное произведение здесь представляет касательное ускорение точки, а второе нормальное ускорение.
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
Сложное или составное движение – это движение точки по отношению к двум системам отсчета, одна из них, связанная с неподвижным толом “B” называется абсолютной, а другая – подвижная система “A” движется относительно неподвижной “B”.

Точка М перемещается внутри или по поверхности тела А, которое еще называется переносной средой (поскольку оно не всегда обязательно твердое). В свою очередь тело А перемещается относительно условно неподвижного тела В.

Пример: движение куска руды относительно конвейера, который перемещается вдоль выработки.

Движение точки М относительно подвижного тела А называется относительным, траектория, скорость такого движения также будут относительными траектории, скорости и ускорения. Относительное движение увидит наблюдатель находящийся вместе с телом А.

Движение точки М вместе с телом А относительно неподвижного тела В, называется переносным движением. Точнее, переносное это движение той точки переносной среды А, относительно неподвижного тела В с которым в данный момент совпадает точка М. Траектория, скорость и ускорение этого движения также соответственно будут переносными траектории скоростью и ускорения.

Движение точки М по отношению к неподвижному телу В или к неподвижной системе отсчета называется абсолютным движением. Именно абсолютное движение видит наблюдатель связанный неподвижным телом В. Траектория, скорость и ускорение - абсолютные траектория, скорость и ускорение.

Пример: движение ползуна вдоль вращающегося кривошипа.



Рис.1.32

Движение ползуна вдоль кривошипа относительное. Фрагментами относительных траекторий будут фрагменты кривых вдоль кривошипа до соответствующих положений ползуна. Переносным движением будет вращательное движение точки К кривошипа, через которые в данный момент проходит ползун. Поэтому фрагментами переносных траекторий будут фрагменты окружностей соответствующего радиуса.

Составным или абсолютным движением будет движение ползуна относительно неподвижного основания, его траекторию получим, соединяя различные положения ползуна Р. В данном случае абсолютная траектория это некоторая разворачивающаяся спираль.