конспект теормех. теоретическая механика
 Скачать 3.7 Mb.
|
|
II. КИНЕМАТИКА ОСНОВНЫЕ ПОНЯТИЯ КИНЕМАТИКИ. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ Изучает движение материальных тел, не интересуясь причинами, вызывающими движение (силами). В кинематике изучается движение лишь с геометрической точки зрения. Кинематику разделяют на кинематику материальной точки и твердого тела. Траектория точки – это пространственная (в общем случае) кривая, которую точка описывает при своем движении. Задавать движение точки - значит указать закон или правило, по которому можно определить положение точки в пространстве в любой момент времени. В кинематике рассматривают три способа задания движения: векторный; координатный; естественный. Время t(с) будет для всех этих способов независимым скалярным аргументом. Векторный способ При этом способе выбирается произвольно неподвижный центр О, и для движущегося по траектории точки М отсчитывается ее радиус-вектор r от этого центра. При движении точки такой радиус вектор изменяет свою величину и направление. Таким образом, он будет векторной функцией скалярного аргумента t. А уравнение  (1) – это записанное в общем виде уравнение векторного способа.Замечание: в дальнейшем считаем доказанным, с векторными функциями можно оперировать по тем же правилам, что и с обычными скалярными. В частности далее будем дифференцировать их по тем же правилам вычисления производных для скалярных функций. Координатный способ При этом способе выбираются какие-либо неподвижные прямоугольные оси, и движение точки в этих осях задается ее прямоугольными координатами как функциями времени. Уравнениями координатного способа тогда будут следующие: x = x(t), y = y(t), z = z(t). Замечание: в дальнейшем полагаем, что функции (2) достаточно гладкие, т.е. они имеют производные до второго порядка включительно. Введем орты прямоугольных осей. При векторном способе будем отсчитывать радиус – вектор точки М от начала координат.  .Последняя формула дает связь между векторным и координатным способами. Отметим, что если движение точки происходит на плоскости, то приняв ее за плоскость Оxy, получим в равенстве (3) лишь два первых слагаемых. Естественный способ П 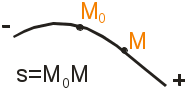 Рис.1.22 ри естественном способе траектория точки должна быть заранее известна. Пусть АВ – часть траектории точки М, выберем на АВ как на обычной координатной оси начало отсчета О, а также положительное и отрицательное направления отсчета. Тогда положение точки М можно задать длинной дуги траектории ОМ с соответственным знаком. Такая величина в кинематике называется криволинейной координатой s, s=ОМ. Уравнением естественного способа лишь одно скалярное уравнение s=s(t). Замечание: если точка движется из начала отсчета все время в положительном направлении, то координата s совпадает с пройденным путем S. Однако в общем случае, когда движение точки может изменять направление, это не так. Связь между естественным и координатными способами. Пусть задан координатный способ, т.е. известны функции (2), тем самым траектория точки задана в осях Oxyz. Поскольку (2) – это параметрическое задание кривой, где t - параметр. Для записи координаты S в естественном способе используем формулу дифференциала дуги пространственной кривой  ds – элементарная длина дуги dx, dy, dz – дифференциалы координат, соответствующие малой длине дуги траектории ds. Введем обозначения:    Замечание: в механике, физике, математике производные по времени обозначают точками. Тогда  Проинтегрируем последнее равенство по времени, тем самым получим S(t):  – связь между координатным и естественным способами.ВЕКТОРЫ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ПРИ КООРДИНАТНОМ СПОСОБЕ. Основными кинематическими характеристиками движения точки является скорость и ускорение, это векторные величины. Вектор скорости. С 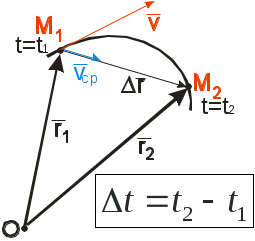 Рис.1.22 редней скоростью точки за время Δt называется отношение  .Переходя в к пределу при  , получим мгновенную скорость, т.е. скорость в момент t.  , скорость точки в данный момент есть производная радиус-вектора по времени  . Поскольку предельное направление хорды М1М2, когда дуга М1М2 стягивается к точке, есть направление касательной в этой точке. Вектор мгновенной скорости  по касательной к траектории (рис.).Ускорение точки. У 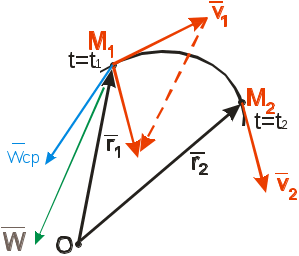 Рис.1.23 скорение характеризует изменение вектора скорости во времени (рис.1.23).Можно доказать, что если дуга траектории М1М2 достаточно мала, то вектор будет направлен в сторону вогнутости траектории.Средним ускорением за время Δt будет отношение  Среднее ускорение направлено в сторону  . Вектор  тем точнее характеризует изменение скорости, чем меньше Δt. Перейдя к пределу при , получим мгновенное ускорение точки, т.е. ускорение в момент t. Вектор мгновенного ускорения, т.е. ускорения в данный момент, равен производной от вектора скорости точки, учитывая, что скорость в свою очередь равна , то  . Вектор  по сказанному раннее также направлен в сторону вогнутости траектории. Если траектория – плоская кривая, то , как и все остальные векторы здесь, лежит в плоскости траектории (рис.1.23). Скорость и ускорение точки при координатном способе задания движения. Запишем связь между векторным и координатным способами.  (1)Поскольку в орты  ,  ,  - постоянные векторные множители, то для определения скорости точки будем дифференцировать по времени, применяя обычные правили дифференцирования, т.е. вынося в каждом из слагаемых орты за знак производной. (2)Если записать вектор  также через его проекции на оси  , то сравнивая это равенство с (2), находим  ,  ,  , т.е. проекциями скорости при координатном способе будут производные от соответствующих прямоугольных координат точки.Величина скорости будет  , направление можно определить направляющими косинусами, т.е. косинусами углов между вектором скорости и осями координат: , , .При вычислении вектора ускорения следует дифференцировать равенство (2) для скорости, тогда, применяя те же правила дифференцирования, получим 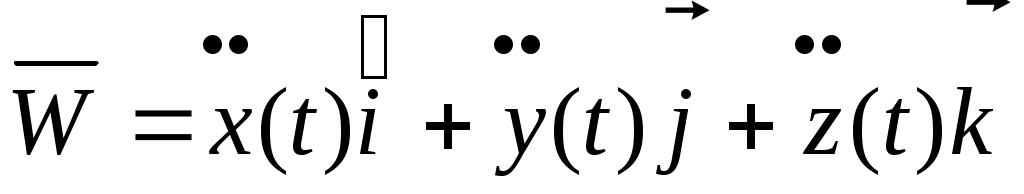 т.е. сразу получаем проекции ускорения  ,  ,  , они равны вторым производным от соответствующих координат.Величина ускорения  .СКОРОСТЬ ТОЧКИ ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ П  Рис.1.24 усть при естественном способе точка М1 в момент t имела криволинейную координату s, а в последующий момент t1 в положении М2 эта координата стала s1, значит за время Δt=t1-t>0 криволинейная координата изменяется на Δs=s2-s1. Для простоты считаем, что Δs>0, т.е. точка движется в положительном направлении. Запишем вектор скорости точки М через предел  или  , (1)т.е. скорость по величине есть производная от криволинейной координаты по времени (рис.). Для записи вектора скорости при естественном способе вводят орт  касательной к траектории, направленный в сторону скорости, тогда  записывается просто:  , где величина V определяется формулой (1).КРИВИЗНА И РАДИУС КРИВИЗНЫ ПЛОСКОЙ КРИВОЙ. ФОРМУЛА ФРЕНЕ. (ПРОИЗВОДНАЯ ОРТА КАСАТЕЛЬНОЙ ПО КРИВОЛИНЕЙНОЙ КООРДИНАТЕ). Кривизна и радиус кривизны плоской кривой. П  Рис.1.25 ри вычислении ускорения для естественного способа будем рассматривать частный случай плоской траектории точки. Все выводы и формулы для этого случая справедливы и в общем случае пространственного движения. Покажем орты касательных к траектории для двух соседних положений точки на ней М0 и М1. Перенесем орт  параллельно в точку М. Угол между ортами ε называется углом смежности. Средней кривизной плоской кривой называют отношение угла смежности к соответствующей длине дуги, т.е.  .В пределе здесь, когда длина дуги  , т.е.  , получим точное значение кривизны, т.е. кривизну кривой в точке М: Величина, обратная К, называется радиусом кривизны  плоской кривой, т.е.  (2); [K]=1/м ,  м.Вычислим радиус кривизны для двух простых случаев: а  Рис.1.26 ) траектория – окружность (рис.) Для окружности угол смежности ε равен соответствующему центральному углу φ, это углы со взаимно перпендикулярными сторонами, поэтому   ,  , т.е. для окружности радиус кривизны совпадает с ее радиусом R.б) траектория – прямолинейная: ε=0, К=0,  Таким образом, для прямолинейного участка траектории радиус кривизны бесконечен. Производная орта касательной по криволинейной координате. При движении точки по траектории орт касательной будет функцией криволинейной координаты s, поэтому имеет смысл производная этого орта по криволинейной координате, которая дается формулой: (формула Френе).Направлена эта производная по внутренней нормали  к траектории в точке ( - радиус кривизны траектории в точке).РАЗЛОЖЕНИЕ УСКОРЕНИЯ ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ НА КАСАТЕЛЬНОЕ И НОРМАЛЬНОЕ. Разложим 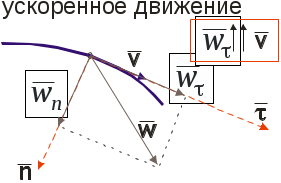 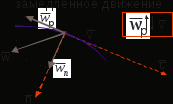графически на две ортогональные составляющие: касательное и нормальное ускорения =  + . Для определения величин Wτ и Wn следует дифференцировать по времени вектор скорости при естественном способе.   Рис.1.27 . Здесь оба множителя зависят от t, поэтому используем формулу дифференцирования произведения  . Здесь во втором слагаемом производную  преобразуем с помощью формулы Френе: .Тогда  . Тем самым нашли векторы касательного и нормального ускорения в  ,  . Касательное ускорение есть производная от величины скорости, а нормальное равно квадрату скорости деленному на радиус кривизны. Из рис. видно, что вектор может иметь либо направление , т.е. скорости, когда  (движение ускоренное), либо противоположное направление, когда  (движение замедленное). |