конспект теормех. теоретическая механика

• Название: теоретическая механика
• Анкор: конспект теормех
• Дата: 03.04.2022
• Размер: 3.7 Mb.
• Имя файла: Konspekt-1_Teor_Mekh.doc
• Тип: Протокол; #437783
• страница: 3 из 7

Теоретическая механика делится на три части:

— Статика,

— Кинематика,

• 
  Динамика.
  

Курс теоретической механики лежит в основе ряда инженерных дисциплин: курсов сопротивления материалов, теории машин и механизмов, строительной механики, теории колебаний, гидравлики.

I. СТАТИКА

Статика изучает равновесие абсолютно твердых тел под действием приложенных к ним сил.

Тело называют абсолютно твердым (недеформированным), если расстояния между любыми двумя его точками неизменны.

Сила – векторная величина, которая характеризуется модулем, направлением и точкой приложения F, размерность: [F] = Н (кН).

В курсе теоретической механики мы не будем интересоваться физической природой действующих сил.

Две системы сил, оказывающие на твердое тело одинаковое воздействие, называются статически эквивалентными.

Одна сила, статически эквивалентная данной системе сил, называется ее равнодействующей. Не всякая система сил сводится к равнодействующей (например, пара сил).

Система сил называется уравновешенной, или статически эквивалентной нулю, если твердое тело под действием такой системы находится в равновесии. Равнодействующая уравновешенной системы сил принимается в статике равной нулю.
АКСИОМЫ СТАТИКИ:

1) Аксиома об уравновешенных силах. Две силы, приложенные к твердому телу, образуют уравновешенную систему тогда и только тогда, когда они равны по величине и действуют по одной прямой в противоположные стороны:

F₂ = -F₁, F₂ = F₁.

2) К твердому телу можно добавлять или от него отбрасывать любую уравновешенную систему сил. Действие остальных сил при этом не изменится.

С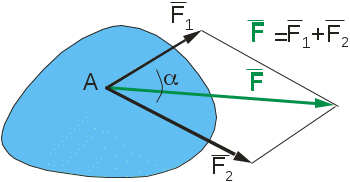


Рис. 1.1
ледствие: Силу в твердом теле можно переносить вдоль линии действия.

Пусть к телу в точке А приложена сила F. Взяв на линии ее действия в теле любую точку В, приложим к ней по первой и второй аксиомам две уравновешенные силы F', F". Взяв F' = F= ­F". Тогда F и F" образуют по первой аксиоме так же уравновешенную систему и по второй их можно отбросить

3) Правило параллелограмма. Две силы, приложенные в одной точке тела, имеют равнодействующую, равную по величине и направлению диагонали параллелограмма, построенного на силах как на сторонах (рис.1.1).

В
ектор F называют геометрической или векторной суммой, а F₁ и F₂ ее составляющими. Модуль равнодействующей:

Замечание: Правило параллелограмма позволяет так же разложить данную силу по двум заданным направлениям.

4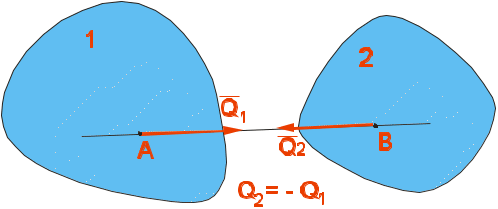


Рис.1.2
) Аксиома взаимодействия. Два твердых тела взаимодействуют друг с другом с силами равными по величине и направленными по одной прямой в противоположные стороны (рис.1.2).

Замечание: Силы, в четвертой аксиоме, формально удовлетворяют условиям первой аксиомы, однако не являются здесь уравновешенными, так как приложены к разным телам.
ПРОЕЦИРОВАНИЕ СИЛ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ. КООРДИНАТНОЕ ПРЕДСТАВЛЕНИЕ СИЛЫ

1


Рис.1.3
. Проекция силы на плоскости:

Пусть сила и ось лежат в одной плоскости. Проекцией плоскости на ось тогда будет отрезок оси между основанием и перпендикулярами, опущенными из концов вектора на эту ось, пр_ОхF = ab = F_х. Проекция величина алгебраическая, то есть это длина отрезка ab со знаком. Она положительна, если угол - острый и отрицательна, если – тупой: F_x = Fcos (рис.3).

2. Проецирование в плоских осях (плоской системе осей):

F_x = Fcos, F_y = Fsin

3. Проецирование в пространстве:

В пространственном случае применяют метод двойного проецирования, то есть проецируют вектор силы сначала на какую-либо координатную плоскость, а полученную проекцию затем на оси координат.

Если известны три проекции на оси, любой вектор F можно записать через орты прямоугольных осей:



(координатное представление вектора силы)

Величина вектора F определяется с помощью теоремы Пифагора.

.

Направление F определяют по направляющим косинусам, то есть косинусами углов между этим вектором и осями:

, ² + ² + ² = 1.
Сходящаяся система сил

Определение Система сил называется сходящейся, если их линии действия пересекаются в одной точке.

Рассмотрим тв. тело под действием сходящейся системы сил. Пусть заданы три силы , и .

,



Точно также последовательно применяя правило параллелограмма, можно найти равнодействующую любой системы n сходящихся сил

.

Вектор называется их геометрической суммой. Он приложен в точке пересечения линий действия сил. Можно показать, что его величина и направление и не зависят от порядка суммирования. Равнодействующую сходящихся сил удобно определять по способу прямоугольника. Равнодействующая по величине и направлению совпадает с замыкающей стороной векторного многоугольника. Если сходящиеся силы не лежат в одной плоскости, этот многоугольник будет пространственным.

Для равновесия тв. тела под действием сходящейся системы сил необходимо и достаточно, чтобы равнодействующая этой системы обращалась в нуль



МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА НА ПЛОСКОСТИ
Сила может не только может толкать тело прямолинейно, но и поворачивать его вокруг той или иной точки. Вращающий эффект силы при этом выражается ее моментом.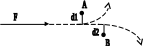



Рис.1.4
Моментом силы, относительно точки (центра) на плоскости называется скалярная величина, равная произведению модуля силы на кратчайшее расстояние от точки до линии действия силы.

М_А(F ) – Момент силы F относительно точки А

М_А(F ) = + F d₁

M _B(F ) = -F d₂

Правило знаков:

d₁ d₂ – плечи силы F относительно точек А и В

Момент силы измеряется (СИ): Н·м.

МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА В ПРОСТРАНСТВЕ
В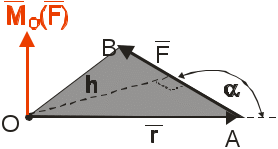


Рис.1.5
пространстве указанное правило знаков теряет смысл, так как на плоскости можно смотреть с разных сторон, поэтому в пространстве момент силы относительно точки принято изображать вектором (рис.)

.

Модуль этого вектора:

М_А (F)=F·d.

Вектор – направлен перпендикулярно плоскости, содержащей радиус-вектор точки А и силу в ту сторону, откуда вращение плоскости видится против хода часовой стрелки.

Из рисунка видно, что площадь треугольника ОАВ равна: S_ОАВ = 0.5АВ · d = =0.5 F · d

Из определения момента: |М_О(F )| = 2S_ОАВ
УРАВНЕНИЕ РАВНОВЕСИЯ ПРОИЗВОЛЬНОЙ ПЛОСКОЙ СИСТЕМЫ СИЛ.

Чтобы тело находилось в покое, необходимо, чтобы отсутствовало поступательное движение вдоль осей и отсутствовало вращение вокруг любой произвольно выбранной точки.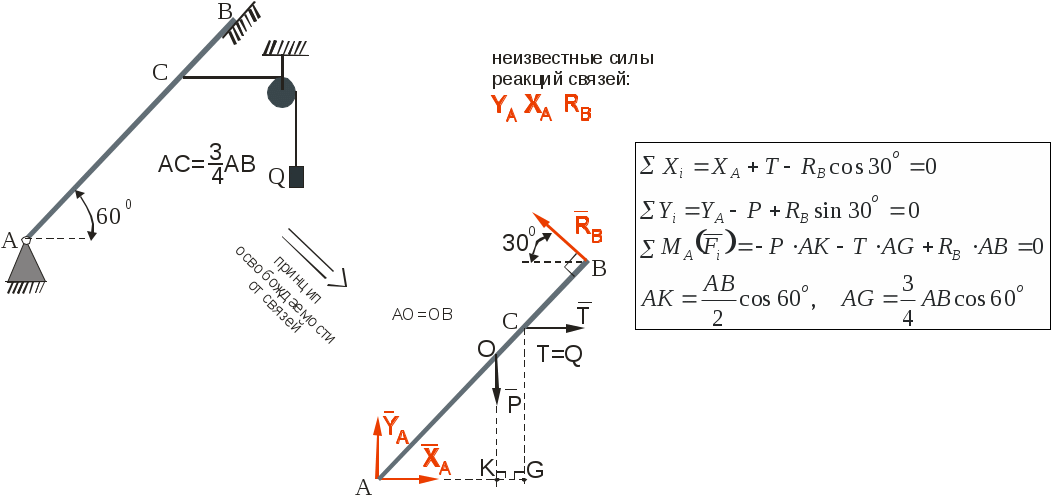

запрещают движение вдоль осей.




Рис.1.7 К составлению уравнений равновесия

запрещает повороты вокруг точки О.
МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ.
Моментом силы относительно оси называется момент её проекции на плоскость относительно точки пересечения оси и плоскости (рис.):



Теорема о связи между моментом силы относительно центра и моментом силы относительно оси: момент силы относительно оси равен проекции на эту ось момента тойже силы относительно любого центра, лежащего на оси.

П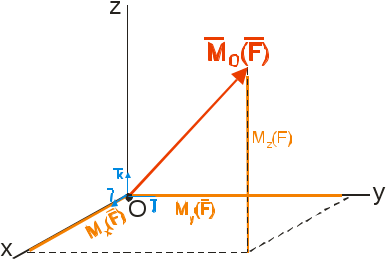


Рис. 1.8
ользуясь этой теоремой можно разложить вектор момента силы относительно начала прямоугольной системы координат по ортам осей (рис.):

.

Коэффициентами в разложении будут являться моменты той же силы относительно осей




Рис.1.9



Теорема (о моменте равнодействующей). Момент равнодействующей относительно оси равен алгебраической сумме моментов составляющих сил относительно той же оси (теорема вариньона).


СВЯЗИ И ИХ РЕАКЦИИ

При решении большинства задач механики приходится иметь дело с телами несвободными, т.е. такими которые соприкасаются или связаны с другими телами и поэтому становятся невозможными те или иные перемещения данного тела.

Связями - называются тела ограничивающие свободу перемещения данного поля. Так для тела лежащего на столе связью является стол, для вала установленного в подшипниках связью является подшипники. Для лестницы приставленной к стене связями является стена и пол. Если на какое либо тело действует сила, то тело будет давить на связь, но в свою очередь связь будет действовать на данное тело. Сила, с которой связь действует на тело и препятствует перемещению называется силой реакции этой связи. По закону равенства действия и противодействия, сила реакции связей по модулю равна силе давления на связь и направлена в противоположную сторону действующей силы.

З


Рис.
адача на равновесие несвободных тел решается в статике на основании следующего очевидного обстоятельства: Всякое несвободное тело можно рассматривать, как свободное, если мысленно освободить его от связей и их действия на тело заменить силами реакции этих связей (принцип освобождаемости, рис.).

Рассмотрим основные типы опор.

1


Рис.1.11

. Гладкая опорная поверхность.

Г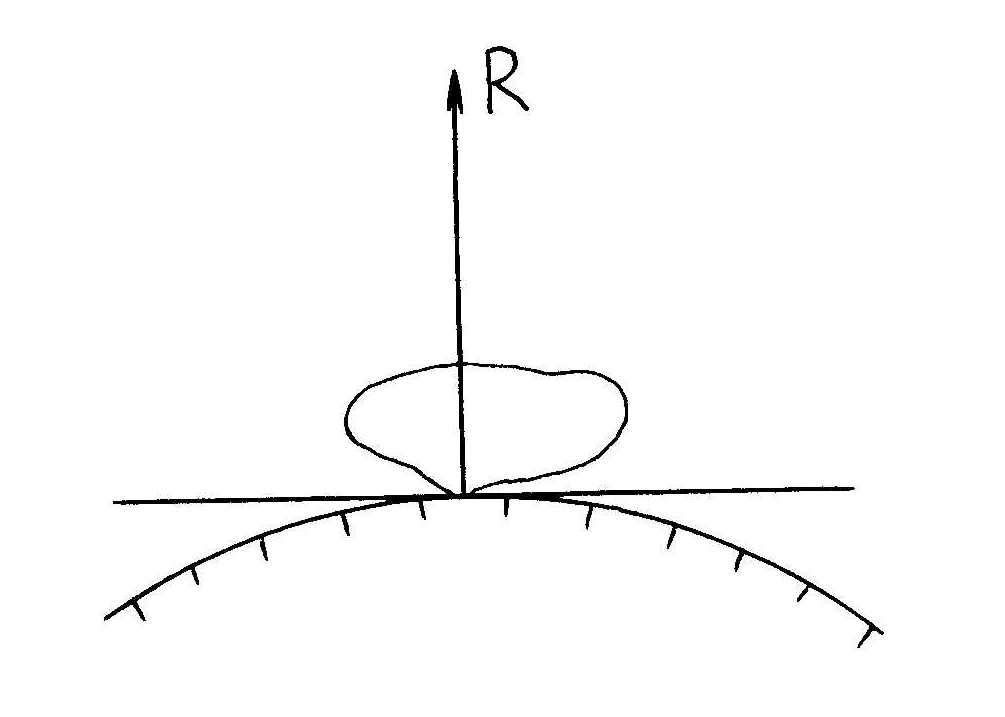


Рис. 1.10

ладкой называется поверхность трением, о которую можно пренебречь. Гладкая опорная поверхность не препятствует скольжению тела и при этом реакция R такой поверхности направлена всегда по нормали.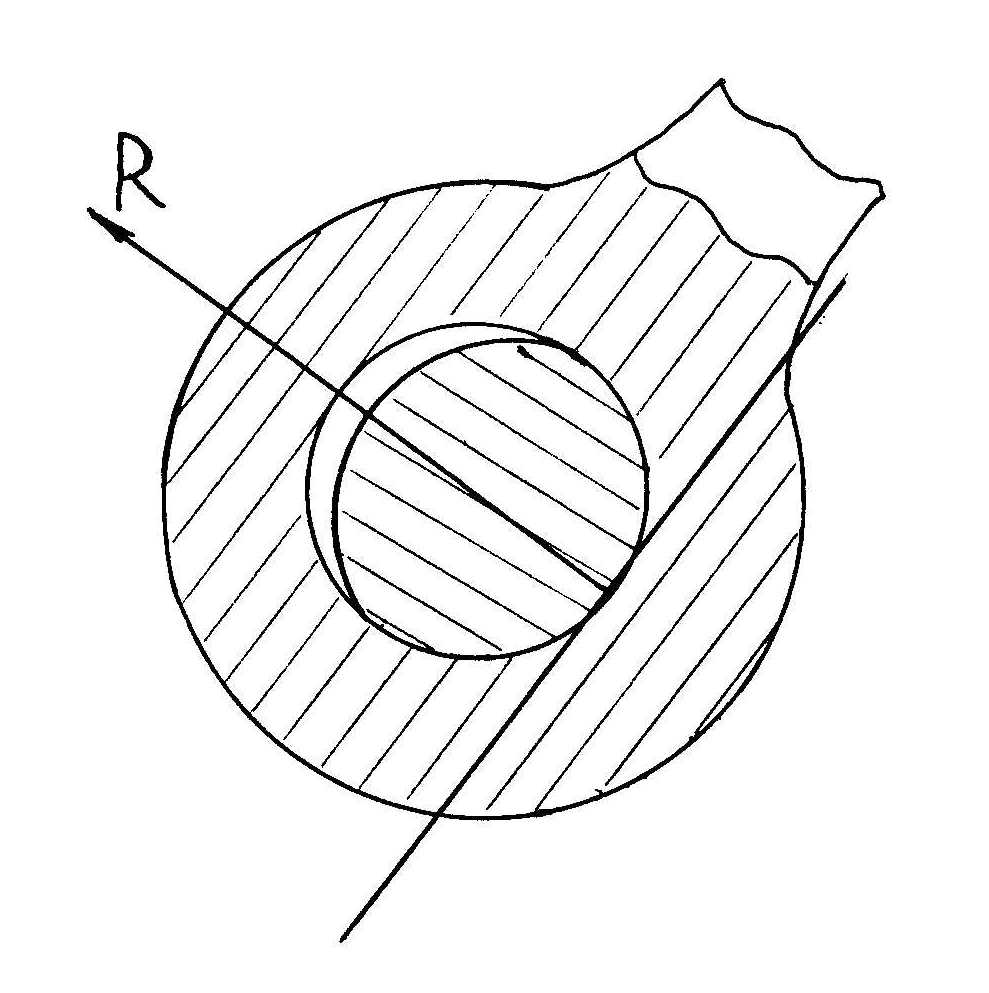




Рис.1.12



2. Цилиндрический шарнир.

Цилиндрический шарнир - это устройство, состоящее из втулки, внутри которой установлена ось. Ось всегда изготавливается диаметром немного меньше, чем диаметр втулки и поэтому эти детали во время работы контактируют по небольшой площадке. Реакция цилиндрического шарнира лежит в плоскости перпендикулярной к его оси. В шарнирных конструкциях часто бывает что сразу направление реакции связи не определить, поэтому вначале определяют составляющие этой реакции, действующие по вертикальным и горизонтальным осям, а за тем определяют равнодействующие связи, усиливая реакцию.
3. Опора на катках.

В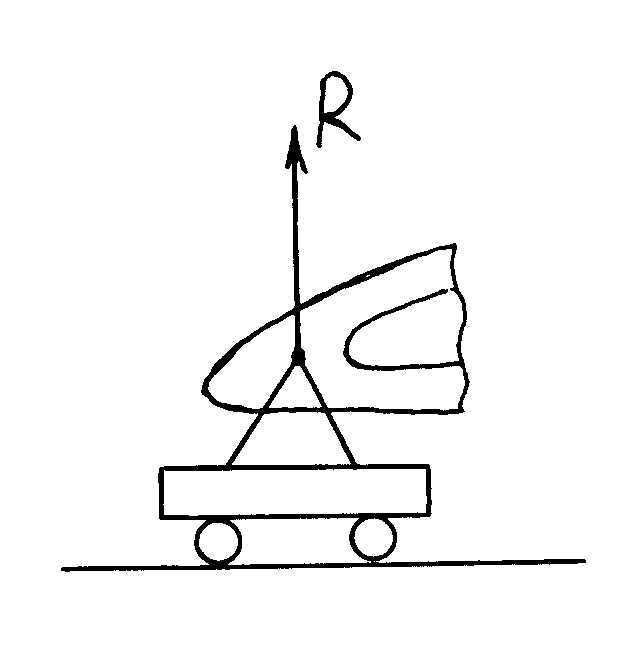


Рис. 1.13
действительности идеально гладких поверхностей и идеально гладких связей не существует, но на практике во многих случаях силой трения можно пренебречь и считать связь идеальной. Примером такой связи является опора на катках. Подвижность катка очень велика, а сила трения очень мала, поэтому в конструкциях такого рода рассматривают реакцию R действующую в вертикальном направлении.
4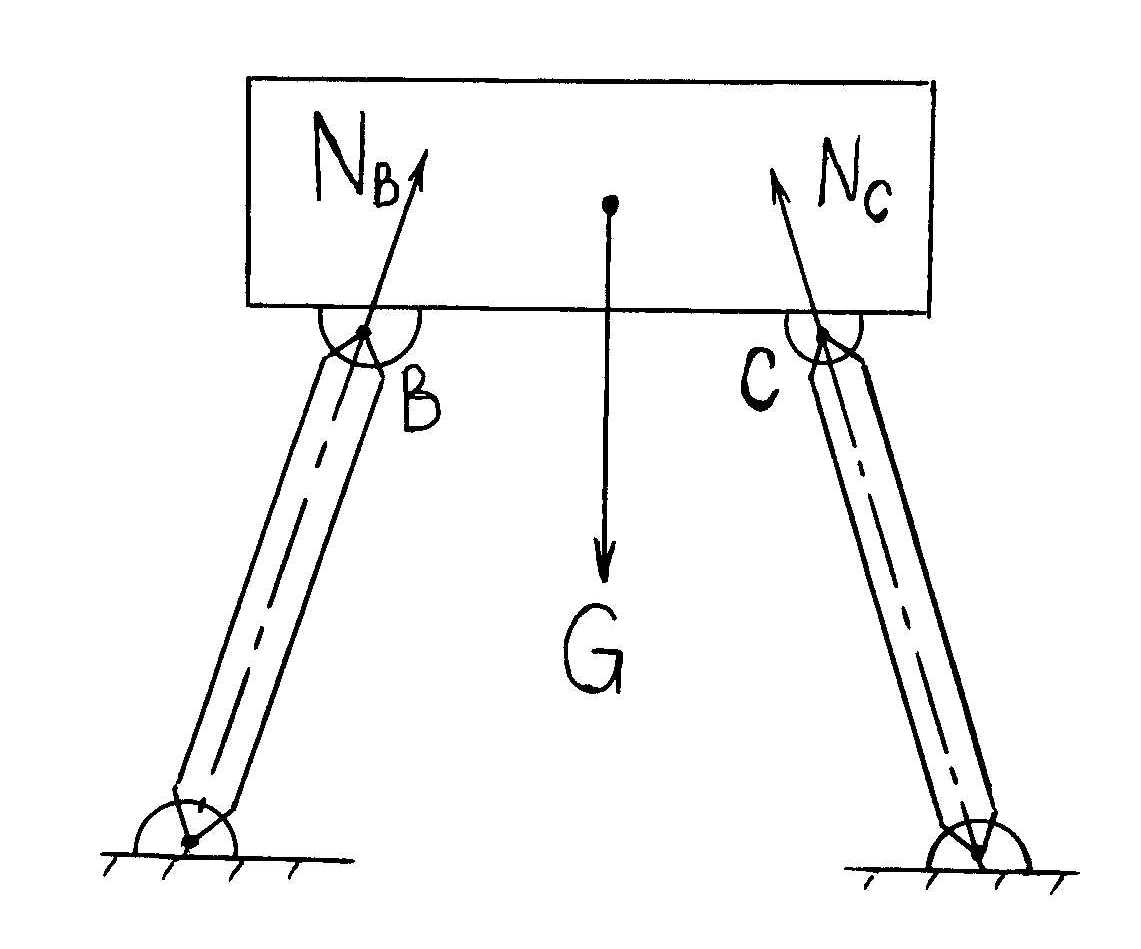


Рис.1.15
. Гибкая связь.




Рис.1.14



Реакция нитей и направлены в противоположную сторону от растягивающих усилий примерами гибких связей являющихся соединением при помощи каната, троса, цепи и арматуры малых диаметров.

5. Шарнирно-стержневые соединения.
Все рассуждения, приведенные для гибкой нити справедливы, если нити заменить жесткими стержнями (не имеющими веса) которые соединены шарнирно, реакции шарнирно закрепленных стержней направлены в противоположную сторону от сил, связывающих нагрузку.
МЕХАНИЧЕСКАЯ ПАРА СИЛ
Парой называется совокупность двух равных по модулю, параллельных, и противоположено направленных сил.

Пара сил характеризует чистое вращение тела, поступательно двигать тело она не может. Пару сил нельзя уравновесить одной силой, у пары нет равнодействующей.

Вращающий эффект механической пары характеризуется ее моментом. Момент пары на плоскости – скалярная величина, определяемая по формуле:



d– плечо пары сил.



Действие пары на тело определяется следующими факторами:

• 
  численным значением момента пары;
  
• 
  направлением вращения пары.
  

Свойства пар сил.

1. 
   Пару сил можно переносить в любое место в плоскости ее действия
   
2. 
   У пары сил можно менять силы или плечо, сохраняя постоянным их произведение, т. е. момент пары.
   
3. 
   Пару можно переносить в параллельную плоскость.
   

Эквивалентные пары

Теорема. Две пары, лежащие в одной плоскости и имеющие численно равные моменты и одинаковое направление вращения – эквивалентны.

Следствие 1. Данную пару, не изменяя ее действия на тело, можно как угодно переносить в ее плоскости, следовательно, действие пары на тело не зависит от положения пары в ее плоскости.

Следствие 2. Не изменяя действие данной пары на тело можно изменять модуль сил и плечо этой пары, но при условии, чтобы ее момент и ее направление вращения остались неизменными.

Следствие 3. Две данные пары всегда можно привести к одному плечу.

Теорема. Данную пару, не изменяя ее действие на тело можно переносить на любую плоскость параллельную плоскости этой пары.

Теорема о сложении пар. Две пары, действующие на тело и расположенные в пересекающихся плоскостях можно заменить одной эквивалентной парой, момент которой равен геометрической сумме моментов слагаемых пар.

Эта теорема справедлива для любого количества пар действующих на тело. Если на тело действует пар с моментами , ,…, , то данная система пар будет эквивалентна одной паре с моментом .
МЕТОД ПУАНСО ПРИВЕДЕНИЯ СИЛ К ПРОСТЕЙШЕМУ ВИДУ, ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ. ЧАСТНЫЕ СЛУЧАИ ПРИВЕДЕНИЯ СИЛ. УРАВНЕНИЯ РАВНОВЕСИЯ ТВЕРДОГО ТЕЛА В ПРОСТРАНСТВЕ.
1. Лемма Пуансо о параллельном переносе силы в твердом теле.

Силу в твердом теле можно переносить параллельно в любую точку, добавляя присоединенную пару сил, причем вектор момента ее равен моменту исходной силы относительно точки переноса: .

2. Метод приведения сил к простейшему виду
Пусть к твердому телу приложена произвольная система сил Выберем в теле произвольный центр приведения (.) О и пользуясь леммой Пуансо перенесем эти силы в центр О, получим систему n – сходящихся сил, векторно равных исходным силам и параллельно присоединенных пар сил.

Сходящихся силы можно заменить одной эквивалентной силой 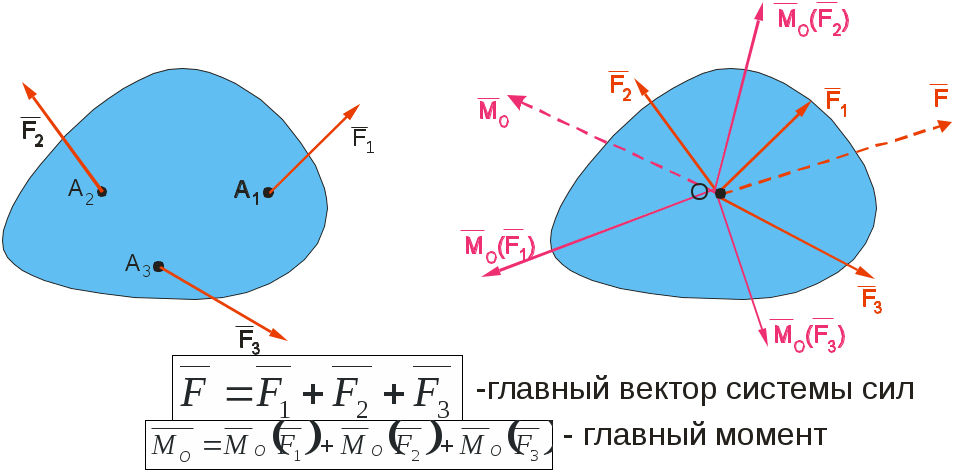- их векторной суммой – главным вектором:




Рис.1.16


Моменты присоединенных пар, пользуясь теорией о сложении сил в пространстве, также суммируем в один главный момент :



Теорема (основная теорема статики). Любую систему n сил в пространстве можно, выбрав произвольный центр приведения, заменить одной силой, их главным вектором , и одной главной парой с моментом .

Главный вектор - есть сумма исходных сил и приложен в центре приведения. Главный момент - есть сумма моментов исходных сил относительно этого центра.

Замечание: Главный вектор не зависит от выбора центра приведения, а главный момент в общем случае зависит.
УРАВНЕНИЕ РАВНОВЕСИЯ ТВЕРДОГО ТЕЛА В ПРОСТРАНСТВЕННОМ СЛУЧАЕ. ЧАСТНЫЙ СЛУЧАЙ РАВНОВЕСИЯ ПЛОСКОЙ СИСТЕМЫ СИЛ.

Запишем условия равновесия тела в векторной форме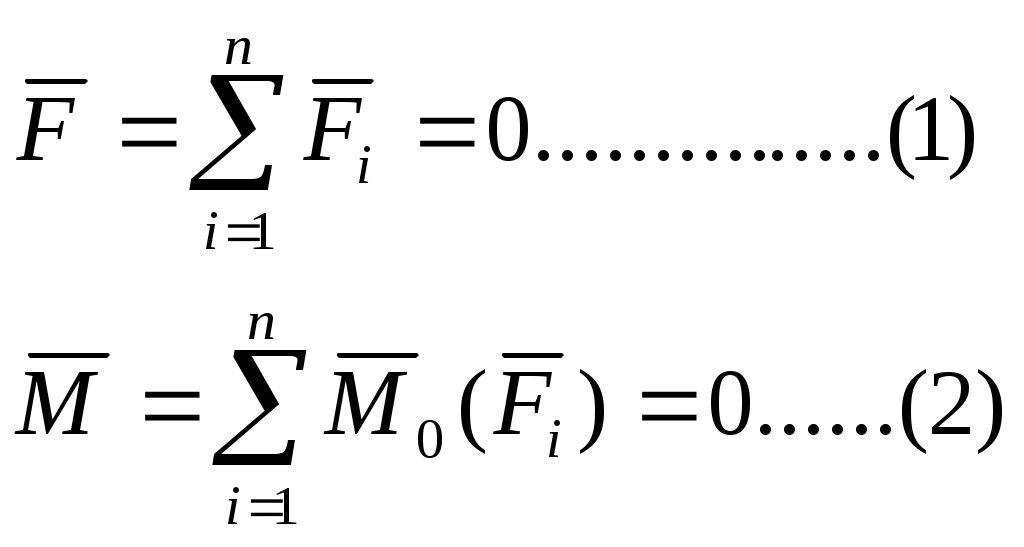



Спроектировав сначала равенство (1) на прямоугольные оси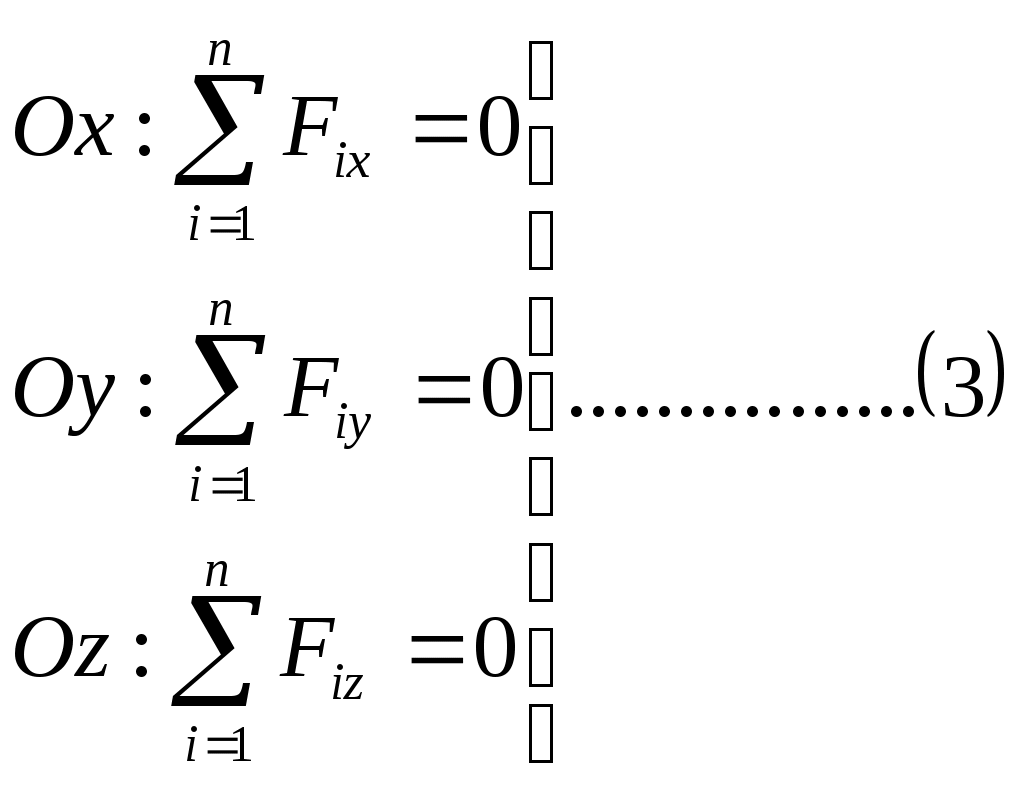

Уравнения в проекциях.

Проецируем равенство (2)

Уравнения моментов.

Таким образом для равновесия тела в пространственном случае, необходимо и достаточно выполнение 6 – ти уравнений равновесия, а именно суммы проекций сил на произвольные оси в пространстве и суммы их моментов относительно тех же осей равны нулю.

Замечание:

1. 
   В уравнения (3) и (4) входят все силы, как известные активные, так и заранее неизвестные реакции опор.
   
2. 
   Задача о равновесии твердого тела в пространстве будет, следовательно, статически определимой, если число неизвестных реакций не превышает шести.