конспект теормех. теоретическая механика

• Название: теоретическая механика
• Анкор: конспект теормех
• Дата: 03.04.2022
• Размер: 3.7 Mb.
• Имя файла: Konspekt-1_Teor_Mekh.doc
• Тип: Протокол; #437783
• страница: 7 из 7

ТЕОРЕМЫ СЛОЖЕНИЯ СКОРОСТЕЙ И УСКОРЕНИЙ В СОСТАВНОМ ДВИЖЕНИИ.

При составном движении точки её абсолютная скорость складывается из векторов относительной и переносной скоростей.



Теорема сложения ускорений.

Здесь вводят вектор угловой скорости переносного вращения. Тогда теорема сложения ускорений записывается так:

Теорема (теорема Кориолиса). Абсолютное ускорение точки является векторной суммой трех ускорений - переносного, относительного и ускорения Кориолиса.

.

Здесь появляется дополнительное ускорение - ускорение Кориолиса, для которого справедливо векторное равенство:

.

Ускорение Кориолиса равно нулю в трех случаях:

1. 
   переносное движение является поступательным и ;
   
2. 
   скорость относительного движения обращается в ноль;
   
3. 
   угол между векторами угловой скорости переносного движения и относительной скорости равен нулю или 180^о.
   

ПЛОСКО ПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА И ЕГО СВОЙСТВА
Д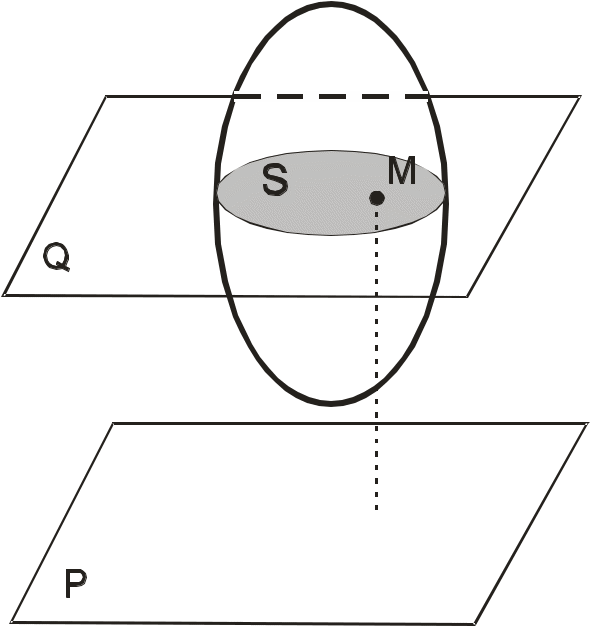


Рис.1.33
вижение твердого тела называют плоскопараллельным (плоским) если любая точка тела во время движения остаётся на одном и том же расстоянии до некоторой неподвижной плоскости “P”.

В соответствии с этим определяем расстояние как от произвольной точки М тела до плоскости Р, так и от любой точки сечения S тела параллельного Р и проходящего через точку М, останется при движении одинаковым.

Последнее означает, что такое сечение S будет скользить в своей плоскости Q параллельно P.

Такое движение совершают многие части механизмов и машин. Например: движение кривошипно -шатунного механизма; качение кругового диска или цилиндра по ровному прямолинейному пути. Это частные случаи плоского движения. Вращение вокруг неподвижной оси рассмотренное ранее, так же частный случай таких движений. Таким образом, чтобы задать плоское движение, достаточно задать движение любого сечения S твердого тела в его плоскости.

Р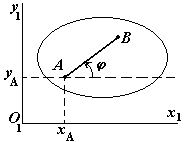


Рис.1.34
ассмотрим движение произвольной фигуры S в её плоскости O₁x₁y₁. Такое движение можно задавать, выбрав в этом сечении любой точку А - полюс и проведя отрезок в произвольную точку В. Последнее же легко задать, задавая движение конца А отрезка его прямоугольными координатами и угол , который отрезок составляет с осью О₁x₁. Следовательно, уравнениями плоскопараллельного движения будут следующие три:

(1)

Таким образом, данные уравнения (1) описывают поступательное движение фигуры S, вместе с плюсом (первые два уравнения) и вращение ее вокруг полюса (третье уравнение). Очевидно, что первые два зависят от выбора полюса, однако угол поворота тела , т.е. вращательная часть плоского движения от выбора полюса не зависит. Последняя есть теорема Эйлера о независимости вращательного движения вокруг полюса.
Скорости точек при плоском движении

Будем определять скорость любой точки В фигуры S движущейся в плоскости O₁x₁y₁, выберем на S произвольный полюс A и свяжем с ним оси 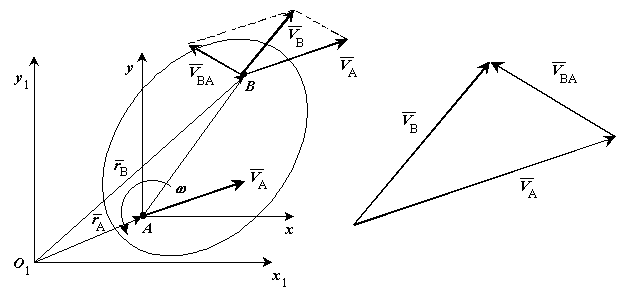параллельные O₁x₁y₁.




Рис.1.35
Движение фигуры S по отношению к осям будет представляться, как вращение вокруг неподвижного центра А (полюса) (рис.). Построим радиус векторы точки В относительно А; - вектор точки В относительно полюса и - вектор полюса относительно неподвижных осей.

(1)

Чтобы определить скорость точки В следует дифференцировать (1) по времени.

(3)

з
б
десь - скорость точки В в неподвижных осях.


а


- скорость полюса в тех же осях.

- вращательная скорость точки М, вокруг полюса А.

(3а)

т.е. любой точке фигуры S складывается из скорости полюса и скорости этой точки во вращательном движении вокруг полюса.

Для определения последней следует знать угловую скорость фигуры S. Заметим, что согласно теореме Эйлера угловая скорость также не зависит от выбора полюса:

Тогда в соответствии с кинематикой вращательного движения имеем, что

. (4)

Скорость перпендикулярна отрезку АВ.

Равенству (3) соответствует треугольник скоростей (рис.1.35 б):

Спроектируем равенство (3) на направление отрезка АМ.

(5)

Получим тем самым следствие из теоремы о равенстве проекций скоростей концов отрезка на его направление.
МГНОВЕННЫЙ ЦЕНТР СКОРОСТЕЙ ПЛОСКОЙ ФИГУРЫ (МЦС).

ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПРИ ПЛОСКОМ ДВИЖЕНИИ МЕТОДОМ МЦС
Мгновенный центр скоростей (точка P) – это такая точка на плоской фигуре S или его мысленном продолжении, скорость которой в данный момент времени равна нулю:

.

Т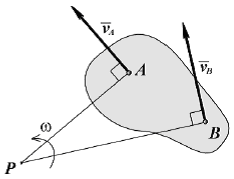


Рис. 1.36
аким образом, можно считать, что фигура S вращается в данный момент вокруг МЦС, однако в отличие от обычного вращательного движения здесь МЦС при движении изменяет свое положение.

Рассмотрим графические случаи определения МЦС.

1) Известны не параллельные друг другу скорости и 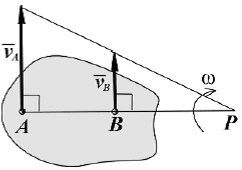двух точек плоской фигуры (рис1.36).

М


Рис. 1.37
ЦС (точка P) находится в точке пересечения перпендикуляров, проведенных через точки A и B к скоростям этих точек. Угловая скорость плоской фигуры равна . О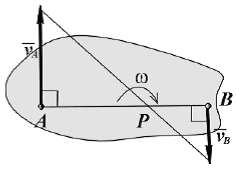тметим, что для нахождения только положения МЦС достаточно знать лишь направления скоростей двух точек.

2


Рис.1.38
) Известны параллельные друг другу скорости и точек A и B плоской фигуры, перпендикулярные отрезку AB, направленные в одну сторону и не равные по модулю ( )(рис1.37).

МЦС (точка P) находится в точке пересечения продолжения отрезка AB и прямой, проведенной через концы векторов и 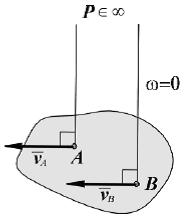. При заданной длине отрезка AB расстояния от МЦС до точек A и B определяются из пропорции .Угловая скорость фигуры .

3


Рис. 1.39
) Скорости двух точек параллельны и равны (рис. 1.39).

Здесь МЦС уходит в бесконечность, поэтому в соответствии с (7) . Это случай мгновенного поступательного движения, для него скорость любой точки М:



4) Известны параллельные друг другу скорости и точек A и B плоской фигуры, перпендикулярные отрезку AB, направленные в разные стороны.

МЦС (точка P) находится в точке пересечения отрезка AB и прямой, проведенной через концы векторов и . При заданной длине отрезка AB расстояния от МЦС до точек A и B определяются из пропорции: . Угловая скорость фигуры .

5) Известно, что скорости и 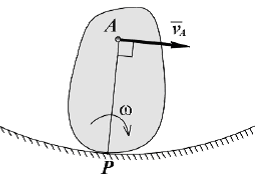двух точек плоской фигуры параллельны друг другу и не перпендикулярны отрезку AB.

М


Рис.1.40
ЦС в данный момент времени не существует или, другими словами, находится в бесконечности. Угловая скорость плоской фигуры в данный момент равна нулю. Движение фигуры называется мгновенно-поступательным.

6) Плоская фигура катится без скольжения по неподвижной кривой.

МЦС (точка P) находится в точке соприкосновения фигуры с кривой, так как скорости точек фигуры и неподвижной кривой, находящиеся в соприкосновении, равны между собой и, следовательно, равны нулю. Если известна скорость какой-либо точки A фигуры, то угловая скорость .

Библиографический список
1. Бутенин Н.В. Курс теоретической механики /Бутенин Н.В., Лунц Я.Л., Меркин Д.Р., М., «Наука», 1985, т.I Статика и кинематика, т.II Динамика.

2. Тарг С. М. Краткий курс теоретической механики. М., Высш. шк., 2003.

3. Мещерский И.В. Сборник задач по теоретической механике. М., Наука, 1986.

4. Нагаев Р.Ф. и др. Теоретическая механика. Методические указания и расчетно - графические задания. РТП ЛГИ, 1981.

5. Бать М.И. Теоретическая механика в примерах и задачах/ Бать М.И. , Джанелидзе Г.Ю., Кельзон А.С. М., «Наука», 1971, т.I Статика и кинематика, т.II Динамика.

6. Сборник задач по теоретической механике/ СПб Горный институт им. Г.В. Плеханова (ТУ). Л.К. Горшков, Р.Ф. Нагаев, Ветюков М.М., В.Н. Монахов, 2004.