теория экономического роста. Теория экономического роста

• Название: Теория экономического роста
• Дата: 12.10.2021
• Размер: 472.76 Kb.
• Имя файла: теория экономического роста.docx
• Тип: Документы; #246130
• страница: 2 из 8

Модель Солоу[править | править код]

Основная статья: модель Солоу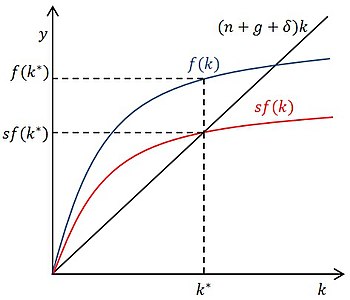



Модель Солоу, фазовая плоскость, равновесие

Модель, объединяющая неоклассическую форму производственной функции с постоянным эффектом от масштаба, убывающей отдачи факторов и положительной эластичностью замены факторов и постоянной нормой сбережения была сформулирована в 1956 году одновременно и независимо друг от друга будущим лауреатом Нобелевской премии по экономике Робертом Солоу^[26] и Тревором Своном (англ.)русск.^[44]. Она приобрела современный вид в 1957 году, когда была дополнена предпосылкой об учёте технологического роста в производственной функции^[45][46].

В модели для производственной функции были приняты неоклассические предпосылки: нейтральность технологического прогресса по Харроду, постоянная отдача от масштаба, убывающая предельная производительность факторов, соответствие условиям Инады и необходимость каждого фактора для производства^{[26][47][48][49]}. Наиболее часто в качестве конкретного примера производственной функции, удовлетворяющей предпосылкам модели, используется производственная функция Кобба — Дугласа^[26][47][50]:

{\displaystyle Y(K,LE)=K^{\alpha }(LE)^{1-\alpha },\ 0<\alpha <1} ,

где {\displaystyle L}  — труд, {\displaystyle K}  — капитал, {\displaystyle E}  — параметр технологического прогресса, {\displaystyle \alpha }  — эластичность выпуска по капиталу, {\displaystyle (1-\alpha )}  — эластичность выпуска по труду.

Поведение потребителей, как и в модели Харрода — Домара, в явном виде в модели не рассматривается. Функция полезности потребителей отсутствует. Вместо этого в модели введена экзогенно задаваемая норма сбережений {\displaystyle s} ^[26][51].

Для поиска решения модели используются удельные показатели на 1 единицу эффективного труда^[52]. В отличие от модели Харрода — Домара, стационарное состояние в модели устойчиво, и описывается следующим условием^[53][54]:

{\displaystyle sf(k^{*})=(n+g+\delta )k^{*}} ,

где {\displaystyle k={\frac {K}{LE}}}  — запас капитала на единицу эффективного труда (капиталовооружённость), {\displaystyle y={\frac {Y}{LE}}=Y{\biggl (}{\frac {K}{LE}},1{\biggr )}=f(k)}  — выпуск на единицу эффективного труда, {\displaystyle k^{*}}  — капиталовооружённость, соответствующая стационарному состоянию, {\displaystyle n}  — темп роста трудовых ресурсов (населения), {\displaystyle g}  — темп технологического прогресса, {\displaystyle \delta }  — норма выбытия капитала.

Модель также позволяет найти такое значение нормы сбережений {\displaystyle s} , при котором потребление на единицу эффективного труда {\displaystyle c={\frac {C}{LE}}}  максимально. Такая норма сбережений {\displaystyle s^{*}}  называется «Золотым правилом» и равна эластичности выпуска по капиталу (то есть, {\displaystyle s^{*}=\alpha }  в случае функции Кобба — Дугласа)^[55].

Модель Солоу дала необходимую математическую базу (построение фазовой плоскости) для анализа темпов изменения капитала и экономического эффекта экономического прогресса^[56], на которой в дальнейшем исследователи создали множество более сложных моделей^[57], потому её считают отправной точкой для всех современных исследований экономического роста^[58][59]. Модель оказала влияние на всю макроэкономическую теорию^[57].

Но вместе с тем, модель Солоу не могла дать объяснение многим проблемам, связанным с экономическим ростом. С теоретической точки зрения, она не показывает, каким образом решения домохозяйств влияют на норму сбережения и, вместе с решениями фирм, на темпы экономического роста. Параметры нормы сбережений и темпов научно-технического прогресса в модели просто задаются экзогенно, решения экономических агентов на них никак не влияют, что не устраивало исследователей^[56][60]. Более того, даже сильная сторона модели — процесс накопления капитала — по сути представляет собой «чёрный ящик», механизм влияния на который экономических агентов в модели не раскрыт^[56].

После появления модели исследователи пытались с её помощью сравнивать ставки процента в разных странах, и это сравнение сразу показало несоответствие модели реальным данным: по модели получалось, что ставка процента в Японии в начале 1950-х годов должна была быть равна примерно 400 %, очень далеко от реальных значений^[60]. Столь сильное отклонение реальных значений ставки процента от теоретических стало причиной развития более сложных моделей, предположения которых относительно процентной ставки были бы более реалистичными. Одни исследователи пошли путём расширения понятия капитал за счёт включения в него человеческого капитала. При таком подходе значение {\displaystyle \alpha }  повышалось с примерно ⅓ до примерно ⅔ (если считать сумму человеческого и физического), и в результате разница в процентной ставке у развитой и догоняющей страны становится намного меньше, чем предсказанная по модели Солоу. Результатом такого подхода стала модель Менкью — Ромера — Вейла. Другие исследователи стали разрабатывать модели, в которых сначала норма сбережений, а потом и темпы экономического роста, не задавались бы экзогенно, а являлись бы следствием решений экономических агентов. Первым шагом в этом направлении стала модель Рамсея — Касса — Купманса, затем дополненная АК-моделями^[61].

Модель Рамсея — Касса — Купманса[править | править код]

Основная статья: модель Рамсея — Касса — Купманса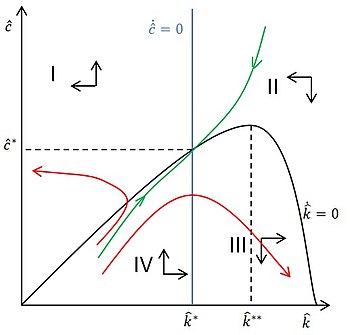



Модель Рамсея — Касса — Купманса, фазовая плоскость

Для объяснения нормы сбережений {\displaystyle s}  как следствия решений экономических агентов, исследователи обратились к работе Фрэнка Рамсея 1928 года, в которой была выведена межвременная функция полезности потребителя и найдено условие оптимального выбора потребителя^[62]. В 1963 году лауреат Нобелевской премии по экономике Тьяллинг Купманс разработал модель, интегрирующую модель Солоу и межвременной выбор потребителя Фрэнка Рамсея^[63], а затем Дэвид Касс (англ.)русск. дополнил её условием трансверсальности^[64], в 1965 году Кумпанс представил окончательную версию модели^[65], названной моделью Рамсея — Касса — Купманса (также известную как модель Рамсея^[66][67][68], неоклассическая модель экономического роста^[66])^{[66][67][69][70]}.

Эта модель сохранила все предпосылки модели Солоу относительно производственной функции. Вместо же экзогенной нормы сбережения, в модель введена межвременная функция полезности потребителя. Предполагается, что между разными поколениями существуют альтруистические связи, и потому его потребительские решения аналогичным решениям бесконечно живущего индивида (или домохозяйства). Эта функция имеет вид^[71][63]:

{\displaystyle U=\int _{0}^{\infty }u(c_{t})e^{-(\rho -n)t}dt} ,

где {\displaystyle c_{t}={\frac {C_{t}}{L_{t}}}}  — потребление на душу населения в момент времени {\displaystyle t} ; {\displaystyle \rho }  — коэффициент межвременного предпочтения потребителя,{\displaystyle \rho >0,\rho =const} .

Бюджетное ограничение индивида в модели имеет вид^[63][72]:

{\displaystyle {\dot {a}}=w_{t}+r_{t}a_{t}-c-na_{t}} ,

где {\displaystyle {\dot {a}}}  — производная активов по времени, {\displaystyle w_{t}}  — заработная плата, {\displaystyle a_{t}}  — активы индивида (могут быть как положительными, так и отрицательными (долг)), {\displaystyle n}  — темп роста трудовых ресурсов (населения), {\displaystyle r_{t}}  — процентная ставка, которая по доходам с активов и по долгу в модели принята одинаковой.

Условие трансверсальности, введённое в модель Дэвидом Кассом, интерпретируется как условие отсутствия схемы Понци (финансовой пирамиды): нельзя бесконечно выплачивать старые долги за счёт новых^[64][73][74]:

{\displaystyle \lim _{t\to \infty }a_{t}e^{-\int \limits _{0}^{t}(r(\nu )-n)d\nu }\geq 0} .

Задача потребителя заключается в максимизации полезности {\displaystyle U}  при бюджетном ограничении и при ограничении на отсутствие схемы Понци. Поскольку бюджетное ограничение представлено как производная по времени, то задача потребителя представлена в виде задачи динамической оптимизации. Её решение можно найти путём построения функция Гамильтона и нахождения её максимума с помощью принципа максимума Понтрягина^[75][76]. Это решение имеет вид:

{\displaystyle {\frac {\dot {c}}{c}}={\frac {1}{\theta }}(r_{t}-\rho )} ,

где {\displaystyle {\dot {c}}}  — производная потребления на душу населения по времени, {\displaystyle {\theta }=-{\frac {u''(c)}{u'(c)}}c}  — эластичность предельной полезности по потреблению, взятая с противоположным знаком.

Оно называется правилом Кейнса — Рамсея, впервые было получено Фрэнком Рамсеем, а содержательную интерпретацию ему дал Джон Кейнс^[62][77].

Наиболее важный вклад модели Рамсея — Касса — Купманса состоит в том, что она раскрыла механизм формирования нормы сбережений через решения потребителей, что стало большим шагом вперёд по сравнению с моделью Солоу, и во многом по этой причине она стала отправной точкой для последующий исследований, которые использовали её концептуальный и математический аппарат, в частности, правило Кейснса — Рамсея, для построения своих моделей^[78]. Неоклассическая модель экономического роста, как и модель Солоу, рассматривается во всех современных учебниках макроэкономики и теории экономического роста^[79]. Однако модель Рамсея — Касса — Купманса по-прежнему не объясняла механизма научно-технического прогресса, в ней он является экзогенной величиной^[79].

Ещё одним недостатком модели некоторые исследователи считали бесконечно живущего индивида (или домохозяйство) в качестве вечного потребителя^[80]. По мере взросления характер потребительского поведения меняется. Если в молодом возрасте индивид работает и делает сбережения, то в старости он эти сбережения тратит^[81]. Этот факт был отражён в модели пересекающихся поколений, которая рассматривает другой крайний случай и полностью отрицает альтруистические связи между поколениями^[82][80].

Модель пересекающихся поколений[править | править код]

Основная статья: модель пересекающихся поколений



Модель пересекающихся поколений, фазовая плоскость, производственная функция Кобба — Дугласа, логарифмическая функция полезности: достижение равновесия

На то, что поведение потребителя меняется с течением времени, обратил внимание будущий лауреат Нобелевской премии по экономике Пол Самуэльсон. В 1958 году он представил простую модель экономики на основе идей Ойген фон Бём-Баверка о причинах существования процентного дохода на капитал, где были выделены три периода жизни индивидуума и соответствующее им потребление (в первых двух он работает, в третьем — выходит на пенсию)^[83]. В 1965 году Питер Даймонд, также будущий лауреат Нобелевской премии по экономике, развил идеи Самуэльсона с учётом выводов модели Солоу и модели Рамсея — Касса — Купманса и представил модель пересекающихся поколений^{[84][80][81][85]}.

Основное отличие от модели Рамсея — Касса — Купманса заключается в том, что жизнь потребителя конечна, и живёт он 2 периода (молодость и старость). Молодой индивид предлагает одну единицу труда (предложение труда неэластично) и получает натуральную заработную плату (неким количеством единственного товара, деньги отсутствуют). Каждый индивид выбирает и разделяет полученное между потреблением в молодости или сбережением и потреблением в старости, максимизируя межвременную полезность своих трат {\displaystyle U} , которая описывается следующей функцией^[84][86]:

{\displaystyle U_{t}={\frac {c_{1t}^{1-\theta }-1}{1-\theta }}+{\frac {1}{1+\rho }}\times {\frac {c_{2t+1}^{1-\theta }-1}{1-\theta }}} .

где {\displaystyle c_{1t}}  — потребление в молодости, {\displaystyle c_{2t+1}}  — потребление в старости.

Межвременное бюджетное ограничение потребителя имеет вид^[84][87]:

{\displaystyle c_{1t}+{\frac {c_{2t+1}}{1+r_{t+1}}}=w_{t}E_{t}} .

Для решения задачи максимизации межвременной полезности {\displaystyle U}  составляется функция Лагранжа и находится её максимум^[87].

В модели пересекающихся поколений, в отличие от модели Рамсея — Касса — Купманса становится возможным динамически неэффективное равновесие с избыточным накоплением капитала, что делает её более реалистичной^[88]. Однако избыточное накопление капитала не является типичной проблемой развивающихся стран, напротив, характеризующихся недостаточным накоплением капитала, потому с точки зрения объяснения проблем развивающихся стран, модель пересекающихся поколений осталась на том же уровне, что и модель Рамсея — Касса — Купманса^[89].

Модель Мэнкью — Ромера — Вейла[править | править код]

Основная статья: модель Мэнкью — Ромера — Вейла



Модель Мэнкью — Ромера — Вейла, фазовая плоскость

Альтернативным путём решения проблемы нереалистичной оценки моделью Солоу процентных ставок в развивающихся странах стало расширение понятия капитал за счёт включения в него человеческого капитала^[90][91]. Результатом такого подхода стала разработанная в 1990 году Грегори Мэнкью, Дэвидом Ромером и Дэвидом Вейлом (фр.)русск. модель Мэнкью — Ромера — Вейла^[92][93](также известная как модель Солоу с человеческим капиталом^[94][95]). В ней использовалась производственная функция Кобба — Дугласа вида^[96][97]:

{\displaystyle Y(K,H,LE)=K^{\alpha }H^{\beta }(LE)^{1-\alpha -\beta },y=k^{\alpha }h^{\beta },0<\alpha ,0<\beta ,\alpha +\beta <1} ,

где {\displaystyle H}  — объём человеческого капитала, {\displaystyle h={\frac {H}{LE}}}  — объём человеческого капитала на единицу эффективного труда, {\displaystyle \beta }  — эластичность выпуска по человеческому капиталу на единицу эффективного труда.

Остальные предпосылки остались теми же, что и в модели Солоу^[96]. В итоге, модель Мэнкью — Ромера — Вейла лучше, чем модель Солоу, описывает межстрановые различия в ВВП на душу населения и темпах его роста благодаря тому, что в развитых странах существенно выше уровень человеческого капитала на душу населения^{[96][98][99][100][101]}. Но при этом она не даёт объяснений причинам этих различий: по модели получается, что бедные страны бедны потому что им недостаёт физического или человеческого капитала, или потому что в них используются неэффективные технологии. Однако почему так происходит — модель не даёт ответа. В определённом смысле она схожа с утверждением о том что бедный человек беден, потому что у него мало денег^[102].