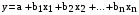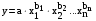Структурировано по ДЕ (тесты с ответами). Тесты 1 де1 основы управления организацией
 Скачать 17.4 Mb. Скачать 17.4 Mb.
|
2.2 Прогнозирование в системе менеджментаПод прогнозированием понимается процесс исследования, направленный на выявление тенденций развития организации и ее внешнего окружения. Целью прогнозирования, прежде всего, является побуждение к размышлению о том, что может произойти во внешней среде и к каким последствиям для организации это приведет. Прогнозирование позволяет оптимизировать деятельность компании, более точно распределить ресурсы. На основе прогнозов строится все планирование производственной и финансовой деятельности организации. В соответствии с прогнозами принимаются решения:
Прогнозирование повышает бдительность менеджеров и, следовательно, их способность реагировать на изменения. Результатом данного этапа является некое научно обоснованное предположение о состоянии системы управления в будущем (прогноз). Для того, чтобы успешно выполнять эту функцию необходимо знать:
Под методами прогнозирования понимается совокупность приемов, позволяющих на основе анализа ретроспективных данных, а также внешних и внутренних связей объекта прогнозирования вывести суждения определенной достоверности относительно его будущего развития. Прежде чем заниматься прогнозированием в компании нам необходимо ответить на ряд вопросов:
Ответы на эти вопросы определяют тип прогноза, способы его получения, время и финансовые ресурсы, которые нам для этого необходимы. Важно, чтобы в компании процесс прогнозирования был определенным образом ФОРМАЛИЗОВАН, т.е. должна быть описана методика его разработки, последовательность прохождения по всем подразделениям с четким указанием применяемых методов построения прогноза, сроков и форм подачи информации. Если это не сделано, то процесс прогнозирования будет происходить стихийно. Выявляя отклонения прогнозных значений от фактических, мы не сможем определить, почему так произошло, соответственно, не сможем сделать выводов для недопущения этих ошибок в будущем, для повышения точности прогнозирования. 2.2 Виды прогнозов
Выбор метода прогнозирования зависит от множества факторов. Отметим некоторые из них:
Методы прогнозирования условно можно разбить на две группы:
Количественные методы прогнозирования требуют значительного количества исходных данных и при их отсутствии не могут быть использованы. Качественные методы, наоборот, предназначены для использования в условиях отсутствия достоверной количественной информации. Методы прогнозирования Качественные методы Каузальные методы Количественные методы Методы анализa временных рядов К количественным методам прогнозирования относятся:
В задачах прогнозирования метод анализа временных рядов используются при наличии значительного количества значений рассматриваемого показателя из прошлого и при условии, что наметившаяся тенденция ясна и относительно стабильна.
К данной группе методов относятся: Метод скользящего среднего Метод проецирования тренда Методы анализа временных рядов Метод экспоненциального сглаживания Модели с аддитивной и мультипликативной компонентой Суть метода скользящего среднего состоит в том, что значение прогнозируемого показателя определяется путем усреднения значений за несколько предшествующих моментов времени. Метод экспоненциального сглаживания также предполагает, суммирование значений за предшествующие периоды времени, но при этом им присваиваются весовые коэффициенты. Взвешивание осуществляется таким образом, что последние данные получают большие веса, нежели более старые. Это связано с тем, что значения показателя за более поздние временные периоды более точно отражают влияние совокупности факторов внешней среды, соответственно они более ценны для прогноза. Для прогнозирования используется следующее рекуррентное соотношение (это означает, что последующий показатель вычисляется через предыдущий) 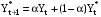 где 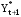 - прогнозируемое значение показателя. - прогнозируемое значение показателя.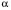 - константа сглаживания. Значение выбирается исходя из конкретных условий. - константа сглаживания. Значение выбирается исходя из конкретных условий. В качестве рекомендаций можно использовать данные следующей таблицы:
k – количество предшествующих моментов времени, используемых в расчете. Пример: Имеются данные о количестве пользователей сети за 7 месяцев текущего года. Необходимо составить прогноз на август месяц методом экспоненциального сглаживания. Константу сглаживания 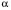 принять равной 0,4. принять равной 0,4.
Для прогнозирования методом экспоненциального сглаживания необходимо провести расчеты для всех временных периодов в следующей последовательности: 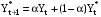 Прогнозное значение за январь месяц примем равным 3 тысяч пользователей, тогда кол-во пользователей в феврале будет равно: 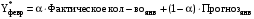 поскольку фактическое и прогнозное кол-во совпадают, то в итоге получим 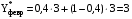 тыс.пользователей тыс.пользователейВ марте: 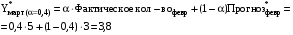 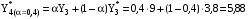 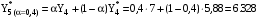 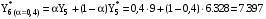 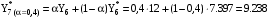 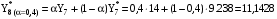 Таким образом, метод экспоненциального сглаживания показал, что в августе количество пользователей будет равно 11,1428 тыс. пользователей.
Метод проецирования тренда Развитие процессов, реально наблюдаемых в жизни, складывается из:
Линии тренда сглаживают динамический ряд, выявляя общую тенденцию. Они позволяют графически отображать тенденции данных и прогнозировать их дальнейшие изменения. Из трендовых моделей в прогнозировании наиболее широко используются следующие виды:
Корректный выбор типа линии тренда, (т.е. обеспечивающей наибольшую точность аппроксимации), во многом определяет качество прогноза. Построение уравнения регрессии сводится к определению её параметров. Для этого используется метод наименьших квадратов (МНК).
В большинстве случаев динамический ряд, кроме тренда и случайных отклонений от него, характеризуется ещё сезонными и циклическими составляющими. Циклические составляющие отличаются от сезонных большей продолжительностью. Обычная продолжительность сезонной компоненты измеряется днями, неделями или месяцами, а циклической – годами или десятками лет. Понятие сезона связано не столько с временами года, сколько с активностью потребления товаров и услуг в течении определенных периодов времени. Данный термин применим к любым систематическим колебаниям. Например, при изучении товарооборота в течении недели под термином сезон подразумевается какие-либо дни недели, характеризующиеся наибольшей активностью покупателей. При изучении транспортных потоков сезонность проявляется не только в днях, но и в часах, можно выделить часы пик с максимальной активностью. Циклические же колебания можно выявить при изучении данных за 10, 15, 20 лет.
Для прогнозирования показателей, подверженных сезонным изменениям может быть использовано 2 типа моделей:
Моделью с аддитивной компонентой называется модель, в которой вариация значений переменной описывается в виде суммы компонент. Аддитивную модель прогнозирования можно представить в виде формулы: F = T + S +E где F – прогнозируемое значение, T – трендовая составляющая, S – сезонная компонента, E – случайная составляющая или ошибка прогноза. Мультипликативная модель – эта модель, в которой вариация значений переменной определяется в виде произведения компонент. Мультипликативную модель можно представить в следующем виде: F = T * S * E Алгоритм анализа сезонности представлен на рисунке: Оценка точности прогноза Для оценки точности прогноза рассчитывают 3 показателя:
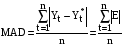 , ,где 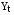 - фактическое значение, - фактическое значение,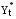 - прогноз. - прогноз.Среднее абсолютное отклонение показывает, на какое количество единиц (например, количество пользователей, тыс.руб. и т.п.) в среднем отклонялся в большую или меньшую сторону наш прогноз. Позволяет определить ошибку в конкретных единицах
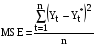 Характеризует вариабельность отклонений в течении рассматриваемого периода.
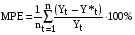 , , 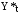 = S + T = S + TВ случае несмещенного прогноза средняя процентная ошибка близка 0. Если MPE <0, то это значит, что прогноз завышен или, иначе говоря, он является переоценивающим В противном случае (MPE >0), то прогноз является недооценивающим. Применение мультипликативных моделей обусловлено тем, что в некоторых временных рядах значение сезонной компоненты представляет собой определенную долю трендового значения. Выбор уровня детализации объектов прогнозированияОдин из наиболее сложных вопросов в области прогнозирования заключается в выборе объекта исследования и уровня детализации. При этом необходимо определить будут ли прогнозироваться обобщающие показатели, характеризующие финансовый результат организации или необходимо составлять прогнозы факторных переменных. Безусловно, детальное прогнозирование – это достаточно трудоемкая задача, но без этого невозможно построить точный прогноз. Декомпозиция позволяет лучше учесть влияние факторов внешней среды и достаточно быстро пересчитывать прогноз при изменении ситуации. Встает вопрос: надо ли строить прогноз по всем продуктам и по всем клиентам или нет? Для ответа на этот вопрос может быть использовано правило Парето.
Позже эту зависимость подтвердили и для других случайных цифр. И она получила название Правила Парето или правила 20/80. Было установлено, что:
Как только появляется массив данных, включающий более 300 случайных измерений, то они пытаются преломиться именно в это соотношение.
Соответственно, чтобы построить достаточно точный прогноз, мы должны уделить особое внимание лишь небольшой части товаров (20%),а остальные 80% товаров можно прогнозировать общим массивом без декомпозиции и на точность прогноза это серьезно не повлияет. Для выбора уровня детализации могут быть использованы метод АВС и XYZ-анализа. Метод АВС-анализа основан на делении определенной совокупности объектов по удельному весу каждой группы, определяемому по тому или иному выбранному показателю. АВС-анализ основан на принципе Парето, который означает, что 20% усилий дают 80% результата, а остальные 80% усилий - лишь 20% результата. Число групп при проведении АВС-анализа может быть любым, но наибольшее распространение получило деление рассматриваемой совокупности на три группы: А, В и С (75:20:5), чем и обусловлено название метода (ABC-Analysis). Группа А включает незначительное число объектов с высоким уровнем удельного веса по выбранному показателю, группа В - среднее число объектов со средним уровнем удельного веса по выбранному показателю, группа С - большое число объектов с незначительной величиной удельного веса по выбранному показателю. Экономический смысл применения АВС-анализа в прогнозных исследованиях сводится к сокращению трудоемкости. Необходимо наиболее тщательным образом прогнозировать товары и услуги, относящиеся к группе А. Таким образом может быть достигнут максимальный эффект при минимальных затратах. Алгоритм проведения АВС-анализа может быть представлен в виде следующего алгоритма:
Для определения принадлежности выбранного объекта к группе необходимо:
Для выделения групп объектов (А, В, С) могут быть использованы различные подходы, наиболее распространенными же являются эмпирический подход и метод касательных. Эмпирический подход заключается в разделении объектов на группы на основе усредненных результатов ранее проведенных исследований, наиболее распространенным является разделение на группы, представленные в таблице Таблица - Разбиение объектов анализа на группы
Для разбиения на группы также может быть использован метод касательных, предложенный Лукинским В.С. Предполагает выполнение следующие последовательности действий: Этап 1 - На основе данных таблицы отсортированной по убыванию построим кумулятивную кривую. Этап 2 – Соединим начало и окончание графика прямой ОZ. Этап 3 – Проведем касательную к кривой АВС, параллельную прямой ОZ. Точка касания N разделит группы А и В. Этап 4 - Теперь соединим точки N и Z и проведем касательную к кривой АВС-анализа, параллельную NZ. Точка касания K разделяет группы В и С. Преимущество метода в его гибкости, простоте и наглядности. Недостатком можно назвать сложность его автоматизации. О Z N K A B C Нарастающий итог доли объектов, % 15% 35% 50% 75% 20% 5% Уд. вес результатов, обеспечиваемых объектами Рисунок – Графическая иллюстрация метода касательных Одновременно с АВС используется XYZ-анализ. Основная идея XYZ-анализа состоит в группировании объектов по стабильности спроса, оцениваемого коэффициентом вариации. Коэффициент вариации рассчитывается по формуле:  , ,В качестве параметра как правила выступает объем продаж. Результатом XYZ –анализа является группировка товаров по трем категориям, исходя из стабильности их поведения:
Объединение результатов АВС и XYZ-анализа позволяет сформировать эффективные решения для каждой типовой группы. Для прогнозирования спроса на товары групп АХ, ВХ и СХ рекомендуется использовать количественные методы. Группы АY, BY, CY характеризуются нерегулярным спросом, что обуславливает необходимость использования комбинированных методик прогнозирования, основанных на сочетании математических подходов и интуитивно-логического анализа, прогнозирование объектов категорий AZ, BZ, CZ целесообразно применять экспертный подход. Каузальные методы прогнозирования Суть каузальных методов прогнозирования состоит в установлении математической связи между результирующей и факторными переменными.
Необходимым условием применения каузальных методов прогнозирования является наличие большого объема данных. Если связи между переменными удается описать математически корректно, то точность каузального прогноза будет достаточно высокой. К каузальным методам прогнозирования относятся:
Каузальные методы Многомерные регрессионные модели Имитационное моделирование Наиболее распространенными каузальными методами прогнозирования являются многомерные регрессионные модели. Многомерные регрессионные модели Многомерная (или многофакторная) регрессионная модель – это уравнение с несколькими независимыми переменными. 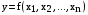 Для построения многомерной регрессионной модели могут быть использованы различные функции, наибольшее распространение получили линейная и степенная зависимости:
В линейной модели параметры (b1, b2, … bn) интерпретируются как влияние каждой из независимых переменных на прогнозируемую величину, если все другие независимые переменные равны нулю. В степенной модели параметры являются коэффициентами эластичности. Они показывают, на сколько процентов изменится в среднем результат (y) с изменением соответствующего фактора на 1% при неизменности действия других факторов.
По мнению одних, данных необходимо в 4-6 раз больше числа факторов. Другие утверждают, что не менее чем в 10 раз больше числа факторов, тогда закон больших чисел, действуя в полную силу, обеспечивает эффективное погашение случайных отклонений от закономерного характера связи. В электронных таблицах Excel имеется возможность построения только лишь линейной многомерной регрессионной модели. Метод имитационного моделирования Монте-Карло
Метод имитационного моделирования Монте-Карло предполагает генерирование случайных значений в соответствии с заданными ограничениями. Приступая к проведению имитационного моделирования, прежде всего, необходимо разработать экономико-математическую модель (ЭММ) прогнозируемого показателя, отражающего взаимосвязь между факторными переменными, а также степень и характер их влияния на результат. Поскольку в условиях современной рыночной конъюнктуры на субъект экономических отношений оказывают одновременное воздействие множество факторов различной природы и направленности и степень их воздействия не является детерминированной, представляется необходимым разделить переменные ЭММ на две группы: стохастические и детерминированные; Далее следует определить типы вероятностных распределений для каждой стохастической переменной и соответствующие входные параметры, выполнить имитацию значений стохастических переменных с использованием генератора случайных чисел MS Excel или иных программных средств. Инструмент «генерация случайных чисел» доступен пользователям MS Excel 2007 после активизации надстройки Пакет анализа. Для выполнения имитационного моделирования в меню ДАННЫЕ необходимо выбрать пункт «Анализ данных», в появившемся диалоговом окне из списка выбрать инструмент «Генерация случайных чисел» и щелкнуть ОК. В появившемся диалоговом окне необходимо для каждой стохастической переменной выбрать тип вероятностного распределения и задать соответствующие входные параметры. Данные этап является одним из наиболее сложных, поэтому при его выполнении необходимо использовать знания и опыт экспертов  Рисунок 1.46 - Интерфейс меню анализа данных Выбор типа вероятностного распределения также может осуществляться на основе имеющейся статистической информации. На практике чаще всего используют такие виды вероятностных распределений как нормальное, треугольное и равномерное.
При важности переменной и невозможности подобрать закон распределения её можно рассматривать с точки зрения дискретного распределения. Перечисленные выше виды вероятностных распределений требуют определения входных параметров, представленных в таблице. Таблица - Входные параметры основных видов вероятностных распределений
В результате проведения серии экспериментов будет получено распределение значений стохастических переменных, на основании которых следует рассчитать значение прогнозируемого показателя. Следующим необходимым этапом является проведение экономико-статистического анализа результатов имитационного моделирования, при котором рекомендуется рассчитывать следующие статистические характеристики:
Указанные выше показатели могут быть использованы для проверки гипотезы о нормальном распределении. В случае подтверждения гипотезы для составления интервального прогноза может быть использовано правило «трех сигм». Правило «трех сигм» гласит, что если случайная величинаX подчинена нормальному закону распределения с параметрами 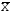 и и 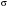 , то практически достоверно, что её значения заключены в интервале , то практически достоверно, что её значения заключены в интервале 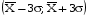 , то есть , то есть 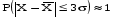 . Для повышения наглядности и упрощения интерпретации целесообразно построить гистограмму. . Для повышения наглядности и упрощения интерпретации целесообразно построить гистограмму.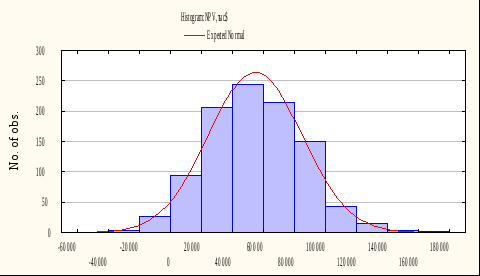 Рисунок 1.48 - Гистограмма значений прогнозируемого показателя Реализация указанных этапов позволит получить вероятностную оценку значений прогнозируемого показателя (интервальный прогноз). |

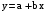 ,
,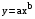 ,
,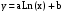 ,
,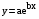 .
.