|
|
УП_Теория статистики_080200 испр.(. Томский политехнический университет н. В. Шаповалова, Н. В. Королева, Т. В. Громова теория статистикИ
Проверь себя
Выберите правильный вариант ответа.
1. К статистической таблице можно отнести:
а) таблицу умножения;
б) опросный лист социологического исследования;
в) таблицу, характеризующую численность населения по полу ивозрасту.
2. Монографические таблицы характеризуют:
а) совокупность единиц изучаемого объекта;
б) группу единиц совокупности по признаку;
в) каждую единицу совокупности.
3. Определите виды статистических графиков по способу построения:
а) линейные;
б) плоскостные;
в) объемные;
г) статистические карты.
4. При изображении структуры и структурных сдвигов в совокупности явлений на графике применяются диаграммы:
а) полосовые;
б) квадратные;
в) секторные;
г) фигур-знаков.
5. Статистический график – это…
а) подробное расписание хода выполнения работ или последовательного изменения состояния чего-либо;
б) некоторая кривая, изображающая зависимость функции от фактора;
в) условное изображение статистических величин и их соотношений посредством линий, геометрических фигур, точек, рисунков или географических карт-схем.
6. Масштабная шкала – это…
а) условная мера перевода статистической величины в графическую и обратно;
б) пространство, на котором размещаются используемые в графике геометрические фигуры;
в) линия, разделенная на равные отрезки точками.
Глава 5
Основные виды обобщающих показателей 5.1. Абсолютные и относительные величины
Абсолютные и относительные величины являются обобщающими статистическими показателями, характеризующими количественную сторону общественных явлений.
 Абсолютные величины характеризуют численность совокупности и объем (размер) изучаемого социально-экономического явления в определенных границах времени и места. Абсолютные величины характеризуют численность совокупности и объем (размер) изучаемого социально-экономического явления в определенных границах времени и места.
Например: численность населения, объем продукции, площадь под зерновыми культурами, число страховых компаний и т.д. Абсолютные величины отражают экономическую мощь страны и социальную жизнь населения (ВВП, ВНД, реальные располагаемые денежные доходы населения, объемы промышленного и сельскохозяйственного производства, объем выпуска важнейших видов продукции).
Различают два вида абсолютных величин: индивидуальные и суммарные. Индивидуальные абсолютные величины характеризуют размеры признака у отдельных единиц совокупности (например, размеры заработной платы отдельного работника, вклады гражданина в определенном банке и т.д.). Они получаются непосредственно в процессе статистического наблюдения и фиксируются в первичных учетных документах. Суммарные абсолютные величины характеризуют итоговую величину признака по определенной совокупности объектов, охваченных статистическим наблюдением. Они могут быть показателями численности совокупности (число предприятий, число студентов, число рабочих) и показателями объема признаков (заработная плата рабочих, объем выпуска товаров и услуг и т.д.).
В зависимости от сущности исследуемого социально-экономи-ческого явления абсолютные величины выражаются в натуральных, стоимостных и условно-натуральных единицах измерения.
Абсолютные статистические величины могут быть как положительными (доходы), так и отрицательными (убытки, потери).
 Относительные величины представляют собой меру количественного соотношения статистических показателей. При расчете относительной величины измеряется отношение двух взаимосвязанных величин (преимущественно абсолютных), что очень важно в статистическом анализе. Относительные величины представляют собой меру количественного соотношения статистических показателей. При расчете относительной величины измеряется отношение двух взаимосвязанных величин (преимущественно абсолютных), что очень важно в статистическом анализе.
Относительные величины вычисляются как отношение двух чисел. При этом числитель называется сравниваемой величиной, а знаменатель – базой относительного сравнения. В зависимости от характера изучаемого явления и задач исследования базисная величина может принимать различные значения, что приводит к различным формам выражения относительных величин.
Относительные величины измеряются:
в коэффициентах, если база сравнения принята за 1, то относительная величина выражается целым или дробным числом, показывающим, во сколько раз одна величина больше другой, или какую часть ее составляет;
в процентах, если база сравнения принимается за 100;
в промилле, если база сравнения принимается за 1000;
в продецимилле, если база сравнения принимается за 10000;
в именованных числах (км, кг, га) и др.
В каждом конкретном случае выбор той или иной формы относительной величины определяется задачами исследования и социально-экономической сущностью, мерой которого выступает искомый относительный показатель. Все используемые на практике относительные статистические показатели можно подразделить на следующие виды:
показатель динамики;
плана;
реализации плана;
структуры;
координации;
интенсивности и уровня экономического развития;
сравнения.
Рассмотрим методы исчисления каждой из них.
 Относительный показатель динамики (ОПД) – показатель, характеризующий изменение величины общественных явлений во времени, который получается делением уровня признака за определенный период (или момент) времени на уровень этого же показателя в предыдущий период (или момент) времени: Относительный показатель динамики (ОПД) – показатель, характеризующий изменение величины общественных явлений во времени, который получается делением уровня признака за определенный период (или момент) времени на уровень этого же показателя в предыдущий период (или момент) времени:
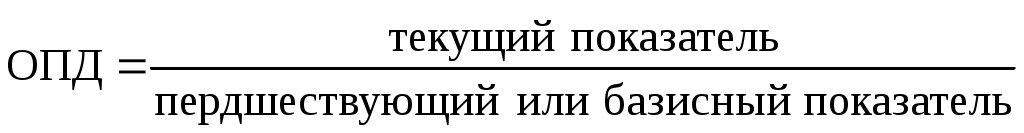 . (5.1) . (5.1)
Этот вид относительных величин широко применяется в планировании, анализе и статистике.
Эта величина показывает, во сколько раз текущий уровень превышает базисный. Если данный показатель выражен кратным отношением, он называется коэффициентом роста, при домножении этого коэффициента на 100 % получают темп роста.
Все предприятия, начиная с индивидуальных и заканчивая крупнейшими корпорациями, обязательно планируют свою деятельность и затем сравнивают полученные результаты с планом или с предшествующим периодом. Для этих целей используют относительный показатель плана (ОПП) и реализации плана (ОПРП).
 Относительный показатель плана (ОПП) рассчитывается как отношение уровня показателя, планируемого на текущий период, к его уровню, достигнутому в предыдущем (базисном) периоде: Относительный показатель плана (ОПП) рассчитывается как отношение уровня показателя, планируемого на текущий период, к его уровню, достигнутому в предыдущем (базисном) периоде:
 . (5.2) . (5.2)
 Относительный показатель реализации плана (ОПРП) представляет собой отношение уровня показателя, фактически достигнутого в текущем периоде, к его уровню, установленному по плану на этот период: Относительный показатель реализации плана (ОПРП) представляет собой отношение уровня показателя, фактически достигнутого в текущем периоде, к его уровню, установленному по плану на этот период:
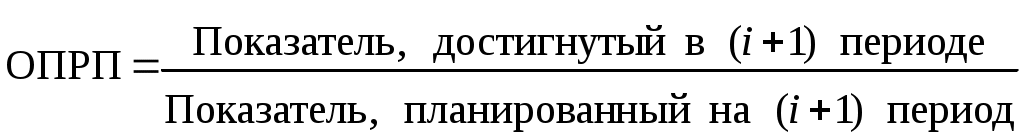 . (5.3) . (5.3)
Между относительными показателями плана, реализации плана и динамики существует следующая взаимосвязь:
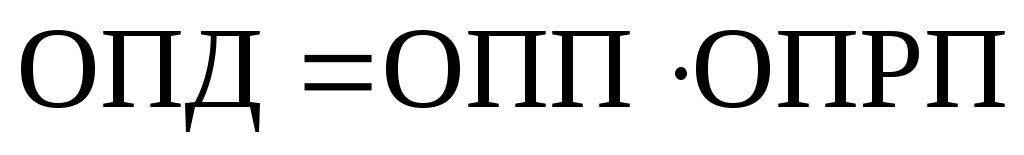 . (5.4) . (5.4)
 Относительный показатель структуры (ОПС) представляет собой соотношение структурных частей изучаемого объекта и их целого: Относительный показатель структуры (ОПС) представляет собой соотношение структурных частей изучаемого объекта и их целого:
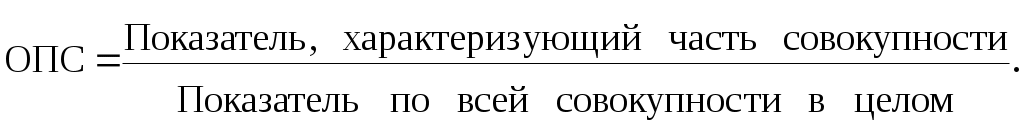 (5.5) (5.5)
 Относительный показатель координации (ОПК) представляет собой отношение одной части совокупности к другой части этой же совокупности. При этом в качестве базы сравнения выбирается та часть, которая имеет наибольший удельный вес или является приоритетной с экономической, социальной или какой-либо другой точки зрения. В результате получают, во сколько раз данная часть больше базисной, или сколько процентов от нее составляет, или сколько единиц данной структурной части приходится на 1 единицу (иногда на 100, 1000 и т.д. единиц) базисной структурной части. Например, соотношение числа мужчин и женщин, отношение численности лиц моложе трудоспособного возраста к численности лиц трудоспособного возраста, отношение объема импорта к объему экспорта и т.д.: Относительный показатель координации (ОПК) представляет собой отношение одной части совокупности к другой части этой же совокупности. При этом в качестве базы сравнения выбирается та часть, которая имеет наибольший удельный вес или является приоритетной с экономической, социальной или какой-либо другой точки зрения. В результате получают, во сколько раз данная часть больше базисной, или сколько процентов от нее составляет, или сколько единиц данной структурной части приходится на 1 единицу (иногда на 100, 1000 и т.д. единиц) базисной структурной части. Например, соотношение числа мужчин и женщин, отношение численности лиц моложе трудоспособного возраста к численности лиц трудоспособного возраста, отношение объема импорта к объему экспорта и т.д.:
 (5.6) (5.6)
 Относительный показатель интенсивности (ОПИ) характеризует степень распространения изучаемого процесса или явления и представляет собой отношение исследуемого показателя к размеру присущей ему среды: Относительный показатель интенсивности (ОПИ) характеризует степень распространения изучаемого процесса или явления и представляет собой отношение исследуемого показателя к размеру присущей ему среды:
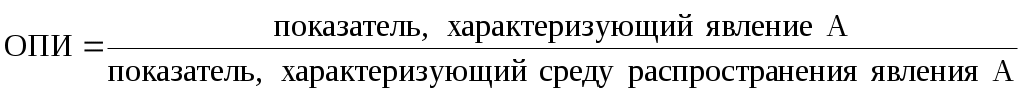 . (5.7) . (5.7)
Среди относительных величин интенсивности в отдельную группу выделяют относительные величины уровня экономического развития, которые представляют собой размеры производства или потребления ВВП, различных видов продукции на душу населения. Эти показатели применяют в территориальных и международных сопоставлениях, по ним судят о степени экономического развития региона или страны.
 Относительный показатель сравнения (ОПСр) представляет собой соотношение одноименных абсолютных показателей, характеризующих разные объекты (предприятия, фирмы, страны, области и т.п.): Относительный показатель сравнения (ОПСр) представляет собой соотношение одноименных абсолютных показателей, характеризующих разные объекты (предприятия, фирмы, страны, области и т.п.):
 (5.8) (5.8)
Различают относительные величины: простые (выполнение договорных обязательств, динамика, структура, пространственное сравнение, координация), составные (относительные величины интенсивности) и сложные (индексы).
В статистическом изучении общественных явлений абсолютные и относительные величины дополняют друг друга. Если абсолютные величины характеризуют как бы статистику явлений, то относительные величины позволяют изучить степень, динамику, интенсивность развития явлений. Для правильного применения и использования абсолютных и относительных величин в экономико-статистическом анализе
необходимо:
использовать достоверные, сопоставимые, сравнительные величины по методике расчета, времени, территории;
вычислять обобщающие показатели на основе полных данных, а не случайных фактов;
применять для характеристики однородные явления;
выбирать правильно знаменатель, который должен быть типичным, а не случайным, т.к. он применяется в виде норматива;
использовать взаимосвязанные абсолютные и относительные величины.
5.2. Средние величины
Средней величиной в статистике называют обобщающий показатель, характеризующий общественное явление по одному количественному признаку в определенных условиях места и времени.
 Статистические средние – это реальные показатели, отражающие объективно существующие свойства общественных явлений (производительность труда, стоимость товара, урожайность, национальный доход на душу населения). Явления существуют в жизни, а статистикой характеризуются в виде определенных показателей. Статистические средние – это реальные показатели, отражающие объективно существующие свойства общественных явлений (производительность труда, стоимость товара, урожайность, национальный доход на душу населения). Явления существуют в жизни, а статистикой характеризуются в виде определенных показателей.
Средняя величина всегда именованная, она имеет ту же размерность, что и признак у отдельных единиц совокупности. Средние величины могут быть как абсолютными, так и относительными (средняя заработная плата, средний процент выполнения плана).
Средняя величина правильно характеризует однородные по своему содержанию совокупности. Такая средняя будет типичной, так как она отражает то общее, что характерно для данной совокупности общественных явлений. Так, например, при исчислении средней урожайности требуется, чтобы исходные данные относились к одной и той же культуре (средняя урожайность пшеницы) или группе культур (средняя урожайность зерновых). Нельзя вычислять среднюю для разнородных культур. Если же совокупность в целом по составу неоднородна, то для получения типичных средних необходимо с помощью метода группировок расчленить такую совокупность на однородные группы и после этого исчислить средние величины для каждой группы отдельно. Так, если рассчитать средний уровень доходов служащих какого-либо района, то получится фиктивный средний показатель, поскольку для его исчисления использована неоднородная совокупность, включающая в себя служащих предприятий различных типов (государственных, совместных, арендных, акционерных), а также органов государственного управления, сферы науки, культуры, образования и т.п.
Исчисление любой средней величины предполагает выполнение следующих условий:
средняя должна вычисляться для качественно однородной совокупности;
для исчисления средней должны быть использованы не единичные, а массовые данные, ибо только тогда взаимопогашаются возможные случайные отклонения.
В зависимости от характера признака, который усредняется, и наличия исходной статистической информации в статистике используют различные виды средних:
средняя арифметическая;
средняя гармоническая;
средняя геометрическая;
средняя квадратическая, кубическая и т.д.
Каждая из перечисленных видов средней может выступать в двух формах: простой и взвешенной. Простая средняя применяется при вычислении средней по первичным (не сгруппированным) данным; взвешенная - по сгруппированным данным.
Средняя арифметическая простая применяется тогда, когда известны индивидуальные значения усредняемого признака и их количество в совокупности:
 . (5.9) . (5.9)
Средняя арифметическая взвешенная применяется в расчетах, когда индивидуальные значения определяемого признака имеют различную частоту повторения:
 , (5.10) , (5.10)
где  – i-й вариант осредняемого признака; – i-й вариант осредняемого признака;
 – вес i-го варианта; – вес i-го варианта;
n– количество вариантов.
Когда отдельные варианты представлены в виде интервалов
«от идо», в качестве варианта принимается середина интервалов. При наличии открытых интервалов границы их устанавливаются условно, исходя из конкретных условий задачи, или с учетом предыдущего интервала. При этом предполагается, что варианты внутри интервала распределяются равномерно. В действительности распределение вариантов внутри интервала может быть неравномерным и середина интервала может не совпадать со средней величиной в интервале. Но при большом числе единиц случайные отклонения взаимно погашаются и полученная средняя достаточно точно покажет типичный размер изучаемого признака.
Используя свойства средней арифметической, можно исчислить ее с помощью способа моментов:
 , (5.11) , (5.11)
где  – индивидуальные значения признака в совокупности; – индивидуальные значения признака в совокупности;
А – середина интервала, обладающего наибольшей частотой;
 – величина интервала; – величина интервала;
 – частота. – частота.
 Пример 2. Рассчитать средний производственный стаж работников предприятия «Агат» по имеющимся данным (табл. 7) двумя способами (по средней арифметической и с помощью способа моментов). Пример 2. Рассчитать средний производственный стаж работников предприятия «Агат» по имеющимся данным (табл. 7) двумя способами (по средней арифметической и с помощью способа моментов).
Таблица 7
Стаж,
лет
|
Число
работников 
|

|

|

|

|
1–4
|
7
|
2,5
|
17,5
|
–1
|
–7
|
4–7
|
10
|
5,5
|
55,0
|
0
|
0
|
7–10
|
8
|
8,5
|
68,0
|
1
|
8
|
10–13
|
6
|
11,5
|
69,0
|
2
|
12
|
13–16
|
9
|
14,5
|
130,5
|
3
|
27
|
16–19
|
5
|
17,5
|
87,5
|
4
|
20
|
Итого
|
45
|
|
427,5
|
|
60
|
Здесь: А – середина интервала с наибольшей частотой, наибольшая частота в данном примере 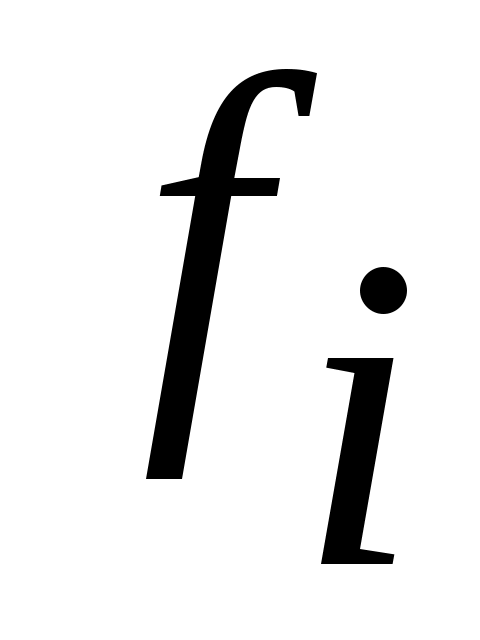 =10, следовательно, А=5,5; h – величина интервала, равная 3 (интервалы равные). =10, следовательно, А=5,5; h – величина интервала, равная 3 (интервалы равные).
Решение. Используя формулу средней арифметической взвешенной (5.10) и формулу расчета средней по способу моментов (5.11), рассчитаем средний производственный стаж работников предприятия «Агат»:


Вывод. Средний производственный стаж работников предприятия «Агат», рассчитанный двумя способами, составил 9,5 лет.
 Средняя гармоническая используется в случае зависимости от характера имеющихся данных, когда существует только одно истинное среднее значение показателя, являющееся следствием реализации его исходного соотношения. Средняя гармоническая используется в случае зависимости от характера имеющихся данных, когда существует только одно истинное среднее значение показателя, являющееся следствием реализации его исходного соотношения.
Если вес каждого варианта равен единице, то при n вариантах формула средней гармонической имеет вид
 . (5.12) . (5.12)
Формула средней гармонической взвешенной следующая:
 , (5.13) , (5.13)
где  ; ;
 –i-й вариант осредняемого признака; –i-й вариант осредняемого признака;
 – вес i-го варианта; – вес i-го варианта;
 – количество вариант. – количество вариант.
 Пример 3. Имеются следующие данные о заработной плате работников фирмы: Пример 3. Имеются следующие данные о заработной плате работников фирмы:
Работники
|
Средняя заработная плата,
р.
|
Фонд заработной платы,
тыс. р.
|
1
|
7800
|
123
|
2
|
9600
|
140
|
3
|
11500
|
162
|
Решение. Исчислим средюю заработную плату по формуле средней гармонической взвешенной (5.13):

 Средняя геометрическая применяется для расчетов средних темпов за определенный период, т.е. тогда, когда определяющий показатель (величина, определяющая вид средней) является не суммой значений, а их произведением: Средняя геометрическая применяется для расчетов средних темпов за определенный период, т.е. тогда, когда определяющий показатель (величина, определяющая вид средней) является не суммой значений, а их произведением:
 (5.14) (5.14)
Этот вид средней используется для вычисления средних коэффициентов (темпов) роста в рядах динамики.
 Средняя квадратическая применяется в тех случаях, когда приходится осреднять величины в виде квадратных функций (например, при расчетах диаметра труб, стволов); в статистике используется как мера вариации. Средняя квадратическая применяется в тех случаях, когда приходится осреднять величины в виде квадратных функций (например, при расчетах диаметра труб, стволов); в статистике используется как мера вариации.
Рассчитывается по формулам (простая и взвешенная):
 (5.15) (5.15)
 (5.16) (5.16)
Средняя квадратическая величина широко применяется при оценке вариации признака, при изучении взаимосвязи явлений.
Правило мажорантности степенных средних состоит в том, что при расчете по одним и тем же данным между числовыми значениями средних, исчисленных по разным формулам, всегда сохраняется следующее неравенство:

5.3. Структурные средние
Особым видом средних величин являются структурные средние. Они применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода, медиана, квартили и децили.
 Модой в статистике называется значение варианты, которое чаще всего повторяется в ряду распределения. Модой в статистике называется значение варианты, которое чаще всего повторяется в ряду распределения.
Способ вычисления моды зависит от вида статистического ряда.
В вариационном ряду это будет варианта, имеющая наибольшую частоту.
В дискретном вариационном ряду модой называют ту варианту, которая имеет наибольшую частоту повторения. Например, по результатам опроса населения относительно определения своего материального состояния по трем оценкам (хорошо, удовлетворительно и неудовлетворительно) большинство респондентов определило свое состояние как неудовлетворительное – это и будет модой. Или модальной ценой на тот или другой товар, продаваемый на рынке, будет та цена, по которой продается максимальное количество товаров. Могут быть распределения, где все варианты встречаются одинаково часто. В этом случае моды нет. В других случаях не одна, а две варианты могут иметь наибольшие частоты. Тогда у признака будут две моды, и распределение будет бимодальным.
В интервальном ряду сначала определяется модальный интервал.
 Модальный интервал – это интервал, имеющий наибольшую частоту встречаемости в исследуемом ряду, а затем определяется значение моды по формуле Модальный интервал – это интервал, имеющий наибольшую частоту встречаемости в исследуемом ряду, а затем определяется значение моды по формуле
 (5.17) (5.17)
где  – нижняя граница модального интервала; – нижняя граница модального интервала;
 – частота модального интервала; – частота модального интервала;
 – частота интервала, предшествующего модальному интервалу; – частота интервала, предшествующего модальному интервалу;
 – частота интервала, следующего за модальным интервалом; – частота интервала, следующего за модальным интервалом;
 – величина модального интервала. – величина модального интервала.
 Медианой называют варианту, которая делит ранжированный (упорядоченный по мере возрастания или убывания) ряд на две равные по объему части. Медианой называют варианту, которая делит ранжированный (упорядоченный по мере возрастания или убывания) ряд на две равные по объему части.
Медиана для дискретного ряда с нечетным числом вариант будет отвечать средней варианте  , где m – номер кратной варианты первой половины ранжированного ряда. , где m – номер кратной варианты первой половины ранжированного ряда.
В интервальном вариационном ряду медиана вычисляется для середины медианного интервала, за который принимается такой, где сумма накопленных частот превышает половину значений частот ряда распределения. В данном случае формула для расчета медианы имеет вид
 (5.18) (5.18)
где  – нижняя граница медианного интервала; – нижняя граница медианного интервала;
 – частота медианного интервала; – частота медианного интервала;
 – сумма накопленных частот интервалов, предшествующих медианному интервалу; – сумма накопленных частот интервалов, предшествующих медианному интервалу;
 – величина медианного интервала. – величина медианного интервала.
Соотношение моды, медианы и средней арифметической указывает направление и степень асимметрии рядов распределения. В симметричных распределениях все три характеристики совпадают. Чем больше расхождение между модой и средней арифметической, тем более асимметричен ряд. Для умеренно асимметричных рядов разность между модой и средней примерно в три раза превышает разность между медианой и средней, т.е. 
Таким образом, мода и медиана являются важными дополнительными характеристиками к средней изучаемой совокупности. Особенно ценны эти показатели для характеристик небольших по численности совокупностей.
Для характеристики структуры вариационного ряда, кроме моды и медианы, в статистике исчисляются и другие характеристики: квартили, децили, процентили.
 Квартили делят ранжированную совокупность по сумме накопленных частот на четыре равные части: нижний квартиль ( Квартили делят ранжированную совокупность по сумме накопленных частот на четыре равные части: нижний квартиль ( ) отделяет ¼ часть совокупности с наименьшими значениями признака; определяется по накопленной частоте, первой превышающей значение 25% от всей совокупности; верхний квартиль ( ) отделяет ¼ часть совокупности с наименьшими значениями признака; определяется по накопленной частоте, первой превышающей значение 25% от всей совокупности; верхний квартиль ( ) отделяет ¼ часть совокупности с наибольшими значениями признака; определяется по накопленной частоте, первой превышающей значение 75% от всей совокупности. ) отделяет ¼ часть совокупности с наибольшими значениями признака; определяется по накопленной частоте, первой превышающей значение 75% от всей совокупности.
Средним квартилем ( ) является медиана. ) является медиана.
В интервальном вариационном ряду квартили внутри определенного по накопленным частотам интервала рассчитываются по следующим формулам:
 ; (5.19) ; (5.19)
 (5.20) (5.20)
где  – нижняя граница интервала, содержащего нижний квартиль; – нижняя граница интервала, содержащего нижний квартиль;
 –нижняя граница интервала, содержащего верхний квартиль; –нижняя граница интервала, содержащего верхний квартиль;
 –величина интервала, содержащего нижний квартиль; –величина интервала, содержащего нижний квартиль;
 – величина интервала, содержащего верхний квартиль; – величина интервала, содержащего верхний квартиль;
 –сумма накопленных частот интервалов, предшествующих интервалу, содержащему нижний квартиль; –сумма накопленных частот интервалов, предшествующих интервалу, содержащему нижний квартиль;
 – сумма накопленных частот интервалов, предшествующих интервалу, содержащему верхний квартиль; – сумма накопленных частот интервалов, предшествующих интервалу, содержащему верхний квартиль;
 – частота интервала, содержащего нижний квартиль; – частота интервала, содержащего нижний квартиль;
 – частота интервала, содержащего верхний квартиль. – частота интервала, содержащего верхний квартиль.
 Кроме квартилей, в вариационных рядах распределения могут определяться децили – варианты, делящие ранжированный ряд по сумме накопленных частот на десять равных частей. Первый дециль (d1) делит совокупность в отношении 1/10 к 9/10, второй дециль (d2) – в соотношении 2/10 к 8/10 и т.д. Вычисляются они по той же схеме, что и медиана, и квартили. Кроме квартилей, в вариационных рядах распределения могут определяться децили – варианты, делящие ранжированный ряд по сумме накопленных частот на десять равных частей. Первый дециль (d1) делит совокупность в отношении 1/10 к 9/10, второй дециль (d2) – в соотношении 2/10 к 8/10 и т.д. Вычисляются они по той же схеме, что и медиана, и квартили.
Для расчета децилей по интервальному вариационному ряду используют следующие формулы:
для определения первого дециля формула
 ; (5.21) ; (5.21)
для определения второго дециля формула
 , (5.22) , (5.22)
где  – нижняя граница интервала, содержащего первый дециль; – нижняя граница интервала, содержащего первый дециль;
 – нижняя граница интервала, содержащего второй дециль; – нижняя граница интервала, содержащего второй дециль;
 – величина интервала, содержащего первый дециль; – величина интервала, содержащего первый дециль;
 – величина интервала, содержащего второй дециль; – величина интервала, содержащего второй дециль;
 – сумма накопленных частот интервалов, предшествующих интервалу, содержащему первый дециль; – сумма накопленных частот интервалов, предшествующих интервалу, содержащему первый дециль;
 – сумма накопленных частот интервалов, предшествующих интервалу, содержащему второй дециль; – сумма накопленных частот интервалов, предшествующих интервалу, содержащему второй дециль;
 – частота интервала, содержащего первый дециль; – частота интервала, содержащего первый дециль;
 – частота интервала, содержащего второй дециль. – частота интервала, содержащего второй дециль.
Остальные децили вычисляются по такому же принципу.
 Значения признака, делящие ряд на сто частей, называются процентилями. Эта характеристика используется редко. Значения признака, делящие ряд на сто частей, называются процентилями. Эта характеристика используется редко.
 Пример 4. Имеются следующие данные о распределении сотрудников рекламного агенства по уровню оплаты труда, данные представлены в табл. 8 (данные условные). Пример 4. Имеются следующие данные о распределении сотрудников рекламного агенства по уровню оплаты труда, данные представлены в табл. 8 (данные условные).
Рассчитайте средний размер заработной платы двумя способами: по формуле средней арифметической и по способу моментов (от условного нуля).
Вычислите структурные средние: моду, медиану, квартили и децили (первый и девятый). Сформулируйте выводы.
Решение. В интервальном вариационном ряду распределения необходимо прежде всего определить середину каждого интервала ( ), которая рассматривается как среднее значение признака у единиц совокупности, попавших в данный интервал (табл.8). ), которая рассматривается как среднее значение признака у единиц совокупности, попавших в данный интервал (табл.8).
Рассчитаем средний уровень заработной платы по формуле средней арифметической взвешенной (5.10):
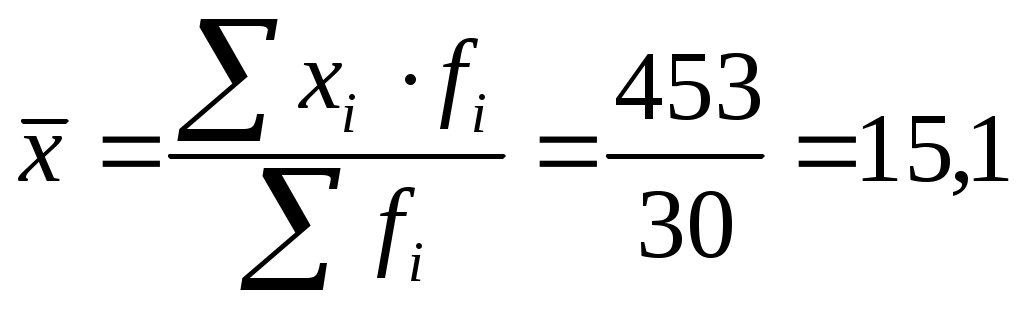 тыс.р. тыс.р.
Таблица 8
Группы сотрудников по уровню заработной платы,
тыс. р.
|
Число сотрудников (чел.)

|
Середина интервала

|
Накопленные частоты
|

|

|
7-10
|
4
|
8,5
|
4
|
34
|
-12
|
10-13
|
6
|
11,5
|
10
|
69
|
-12
|
13-16
|
7
|
14,5
|
17
|
101,5
|
-7
|
16-19
|
8
|
17,5
|
25
|
140
|
0
|
19-22
|
3
|
20,5
|
28
|
61,5
|
3
|
22-25
|
2
|
23,5
|
30
|
47
|
4
|
|
30
|
-
|
-
|
453
|
-24
|
Для того чтобы рассчитать средний уровень заработной платы по способу моментов, применим формулу (5.11).
При расчете среднего числа по способу моментов необходимо определить величину А. Величина А – условный нуль, который определяется как середина интервала с наибольшей частотой. В данном примере А=17,5 [т.к. наибольшая частота (8) соответствует интервалу
16-19, середина интервала –17,5]. Величина интервала  =3. =3.
Произведем вспомогательные расчеты в табл. 8.
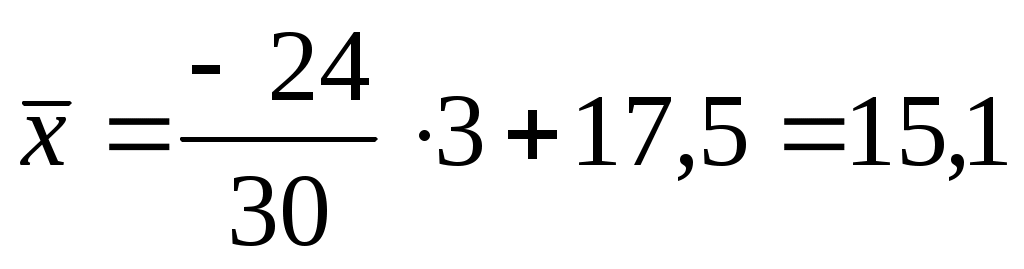 тыс.р. тыс.р.
Вывод. Средний уровень заработной платы у сотрудников рекламного агентства, рассчитанный двумя способами, составил 15,1 тыс. р.
Рассчитаем структурные средние величины:
1. Мода. Для того чтобы определить моду, необходимо найти модальный интервал: наибольшая частота 8 соответствует интервалу
16–19; этот интервал будет модальным.
Модальный интервал (16–19). Определим составляющие формулы (5.17):
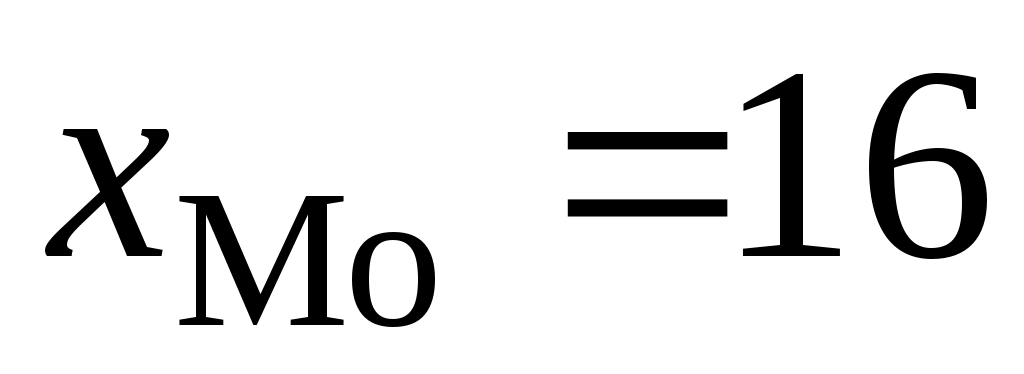 – нижняя граница модального интервала; – нижняя граница модального интервала;
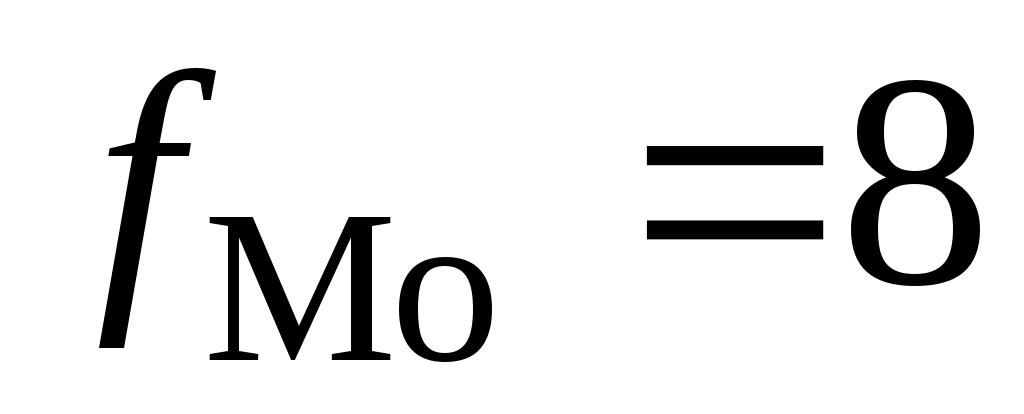 – частота модального интервала; – частота модального интервала;
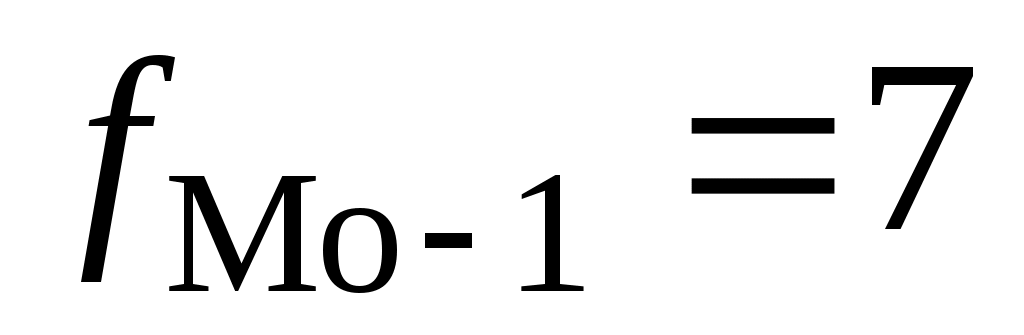 – частота интервала, предшествующего модальному интервалу (предмодальная частота); – частота интервала, предшествующего модальному интервалу (предмодальная частота);
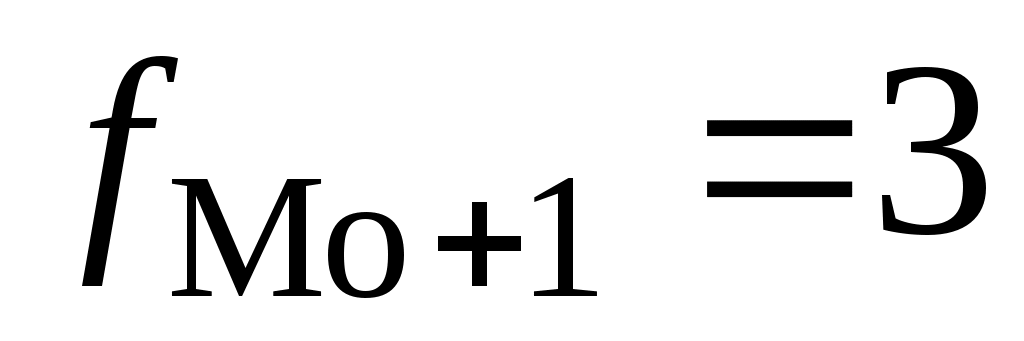 – частота интервала, следующего за модальным интервалом (послемодальная частота); – частота интервала, следующего за модальным интервалом (послемодальная частота);
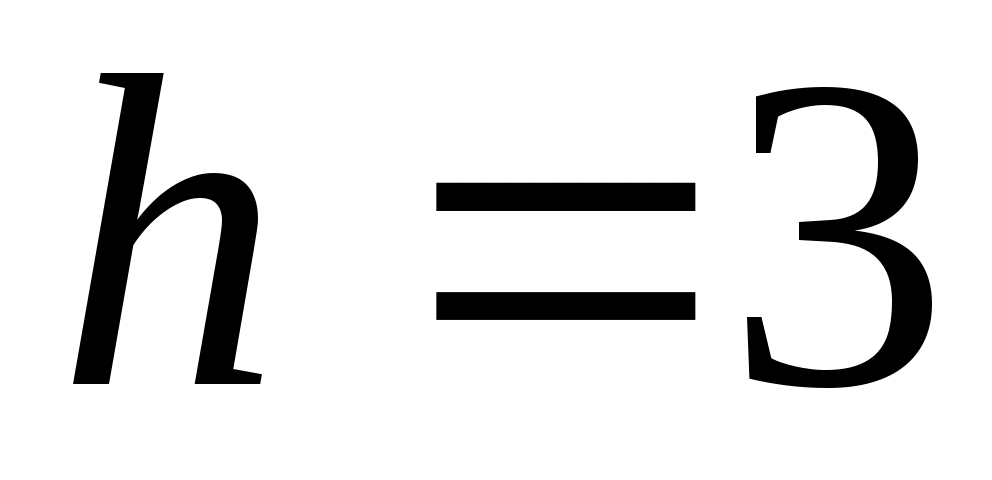 – величина модального интервала. – величина модального интервала.
Подставим все значения в формулу (5.17):
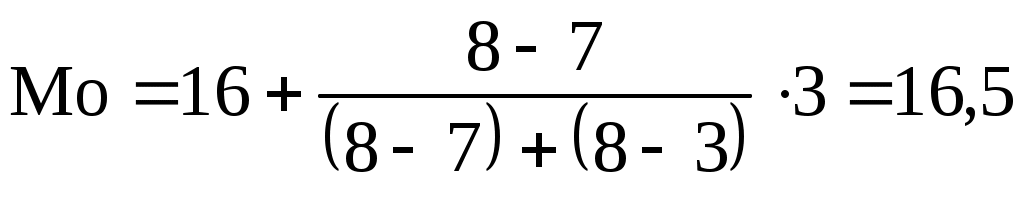 тыс.р. тыс.р.
Вывод. Заработная плата у наибольшего числа сотрудников рекламного агенства составляет 16,5 тыс. р.
2. Медиана. При расчете медианы необходимо определить накопленные частоты (табл.8) для нахождения медианного интервала. Определим медианный интервал: сумму всех частот 30 разделим пополам, получим 15, в графе накопленные частоты находим значение первое, превышающее значение 15, – это число 17, ему соответствует интервал 13–16, он и будет являться медианным интервалом.
Медианный интервал (13–16). Определим составляющие формулы (5.18):
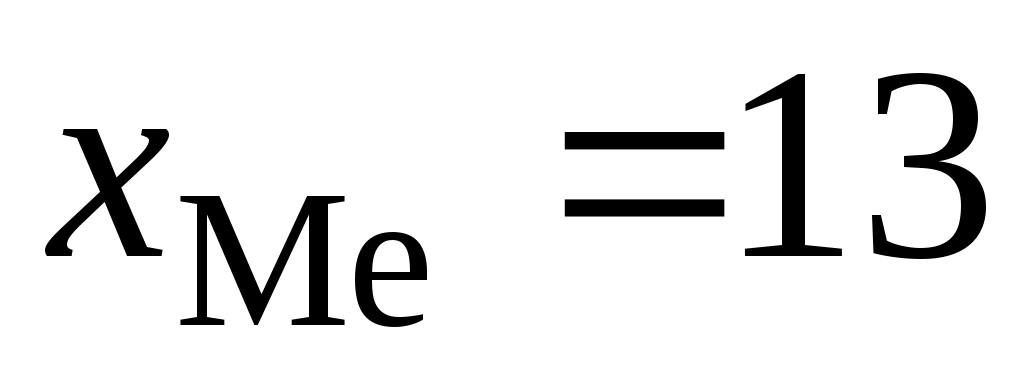 – нижняя граница медианного интервала; – нижняя граница медианного интервала;
 – сумма всех частот; – сумма всех частот;
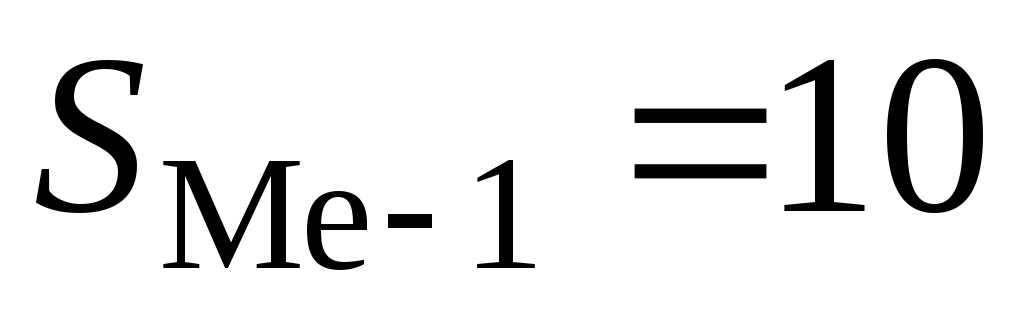 – сумма накопленных частот, предшествующих медианному интервалу; – сумма накопленных частот, предшествующих медианному интервалу;
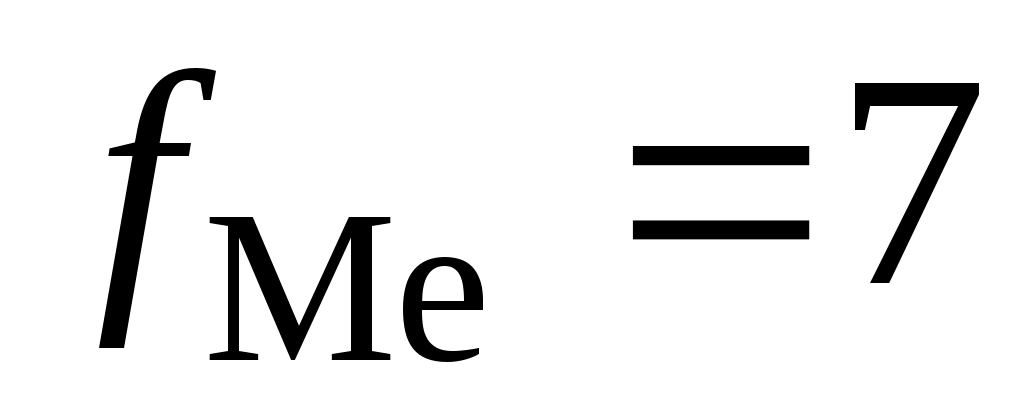 – частота медианного интервала; – частота медианного интервала;
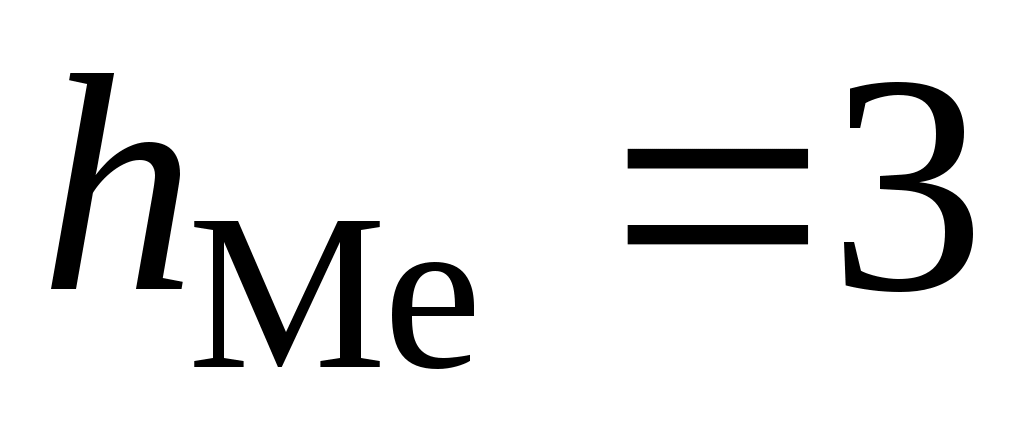 – величина медианного интервала. – величина медианного интервала.
Подставим все значения в формулу (5.18):
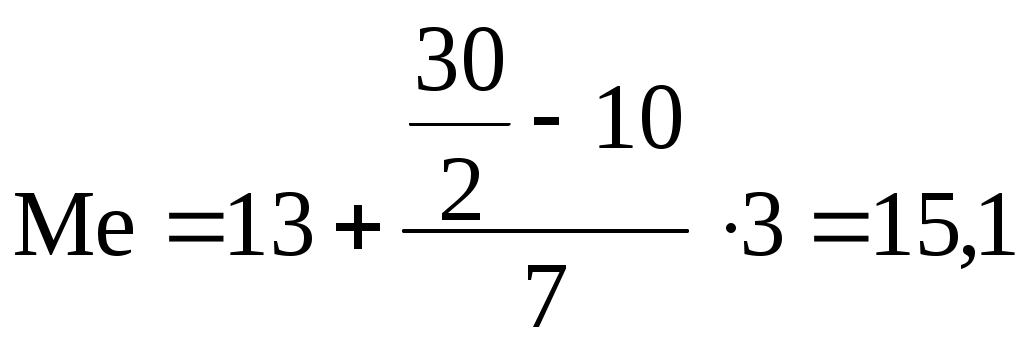 тыс.р. тыс.р.
Вывод. Половина (50%) сотрудника из данной совокупности имеют заработную плату менее 15,1 тыс. р., и половина (50%) сотрудников имеют заработную плату выше 15,1 тыс. р.
3. Квартили. Для расчета квартилей необходимо определить интервалы, содержащие верхний и нижний квартиль. Интервал, содержащий нижний квартиль имеет накопленную частоту, которая первая превышает  (т.е. 25% всей совокупности), (т.е. 25% всей совокупности), 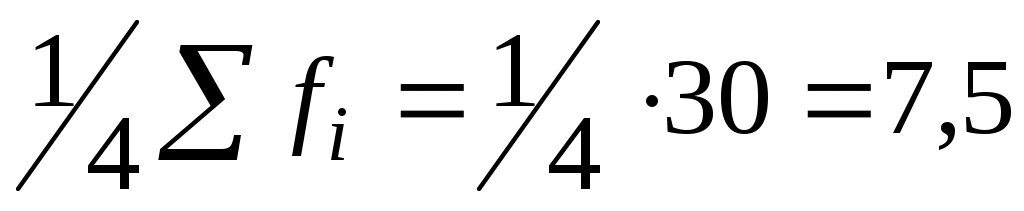 ;в графе накопленные частоты находим значение первое, превышающее 7,5, – это 10; эта частота соответствует интервалу 10–13, значит, этот интервал будет содержать нижний квартиль. ;в графе накопленные частоты находим значение первое, превышающее 7,5, – это 10; эта частота соответствует интервалу 10–13, значит, этот интервал будет содержать нижний квартиль.
Интервал, содержащий нижний квартиль (10–13). Определим составляющие формулы (5.19):
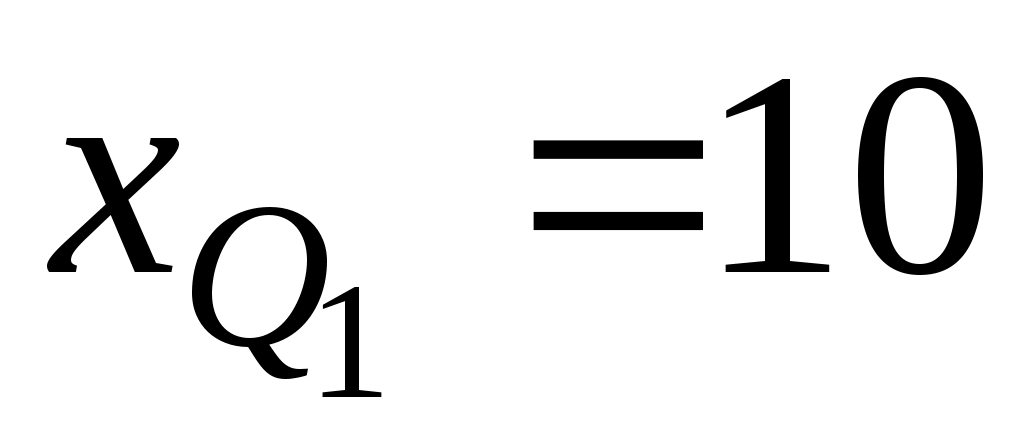 – нижняя граница интервала, содержащего нижний квартиль; – нижняя граница интервала, содержащего нижний квартиль;
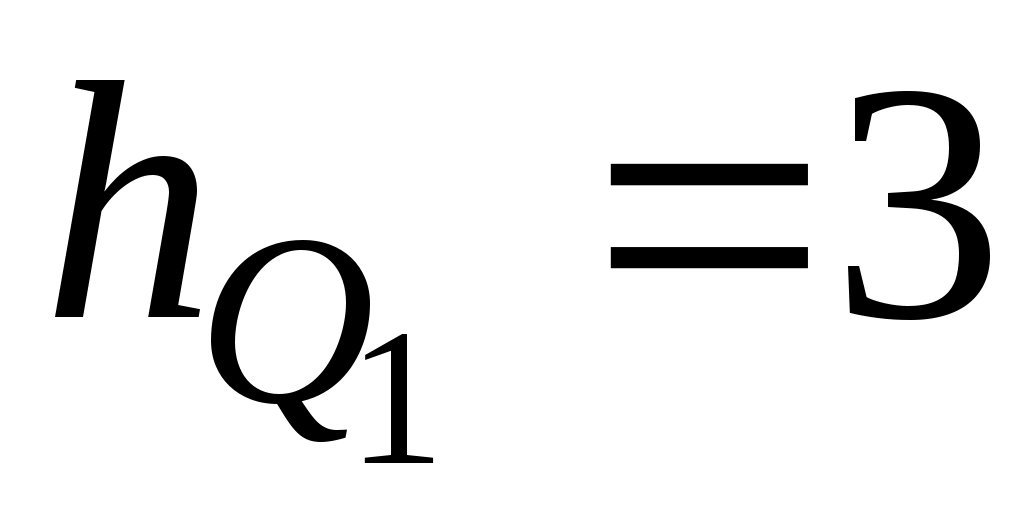 – величина интервала, содержащего нижний квартиль; – величина интервала, содержащего нижний квартиль;
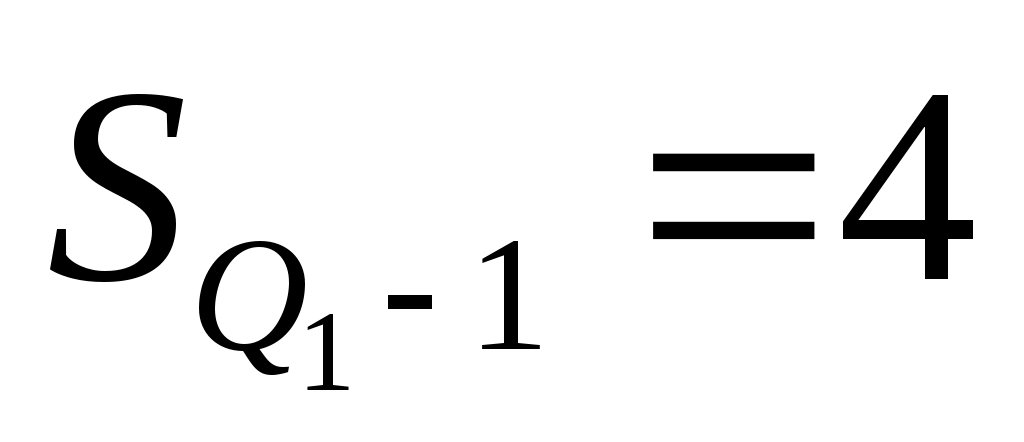 – сумма накопленных частот интервалов, предшествующих интервалу, содержащему нижний квартиль; – сумма накопленных частот интервалов, предшествующих интервалу, содержащему нижний квартиль;
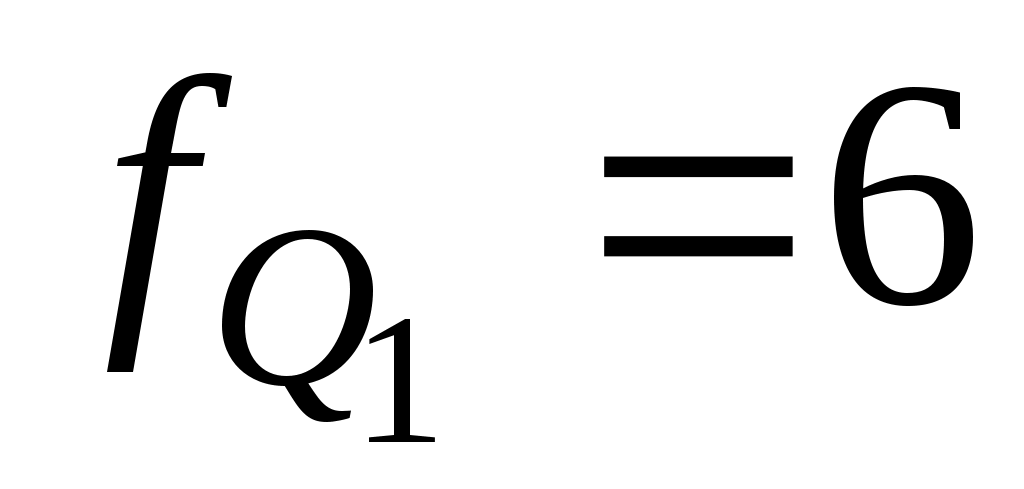 – частота интервала, содержащего нижний квартиль. – частота интервала, содержащего нижний квартиль.
Подставим все значения в формулу (5.19):
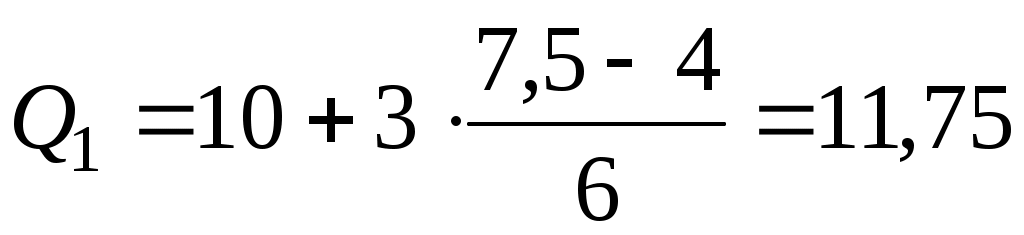 тыс.р. тыс.р.
Интервал, содержащий верхний квартиль имеет накопленную частоту, которая первая превышает 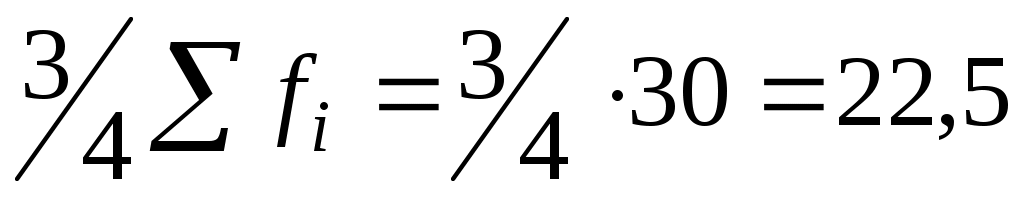 ; в графе накопленные частоты находим значение первое, превышающее 22,5. Это число 25 соответствует интервалу 16–19, значит, этот интервал будет содержать верхний квартиль. ; в графе накопленные частоты находим значение первое, превышающее 22,5. Это число 25 соответствует интервалу 16–19, значит, этот интервал будет содержать верхний квартиль.
Интервал, содержащий верхний квартиль (16–19). Определим составляющие формулы (5.20):
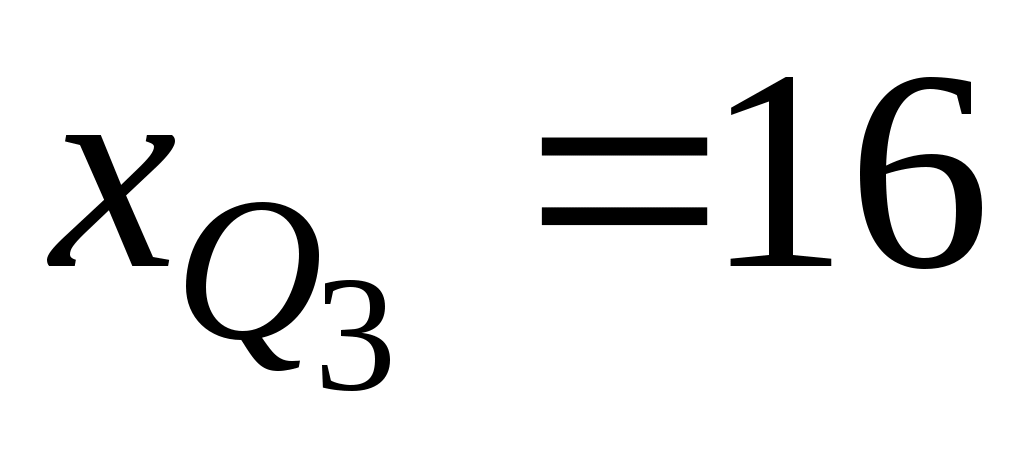 – нижняя граница интервала, содержащего верхний квартиль; – нижняя граница интервала, содержащего верхний квартиль;
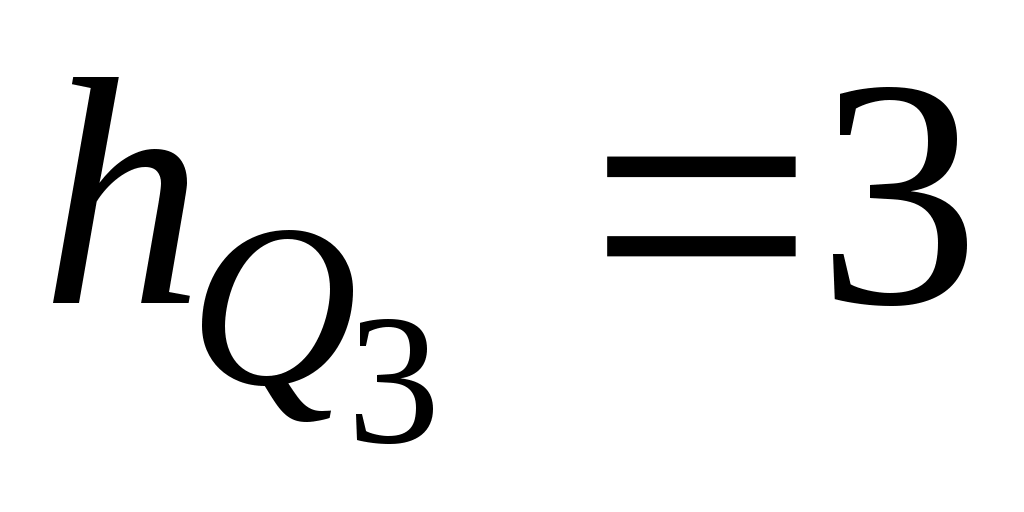 – величина интервала, содержащего верхний квартиль; – величина интервала, содержащего верхний квартиль;
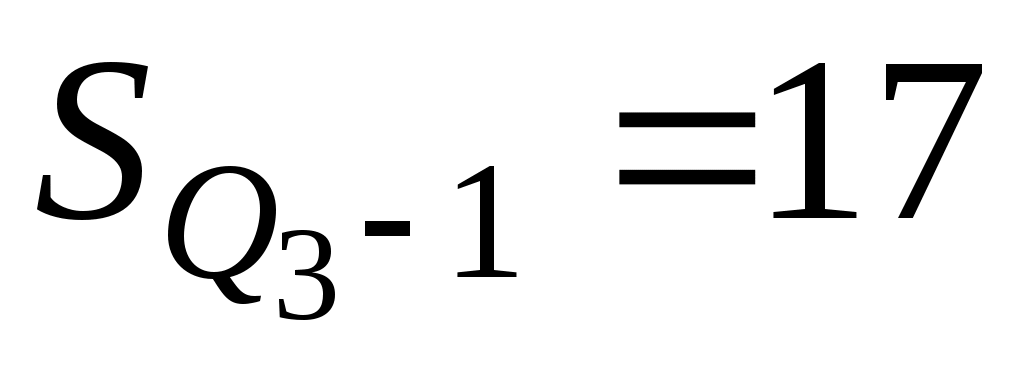 – сумма накопленных частот интервалов, предшествующих интервалу, содержащему верхний квартиль; – сумма накопленных частот интервалов, предшествующих интервалу, содержащему верхний квартиль;
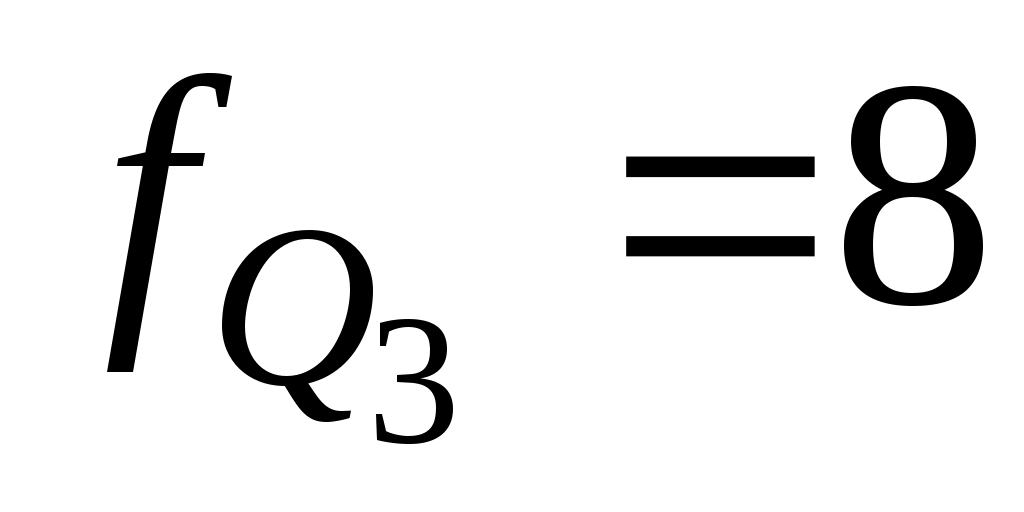 – частота интервала, содержащего верхний квартиль. – частота интервала, содержащего верхний квартиль.
Подставим все значения в формулу (5.20):
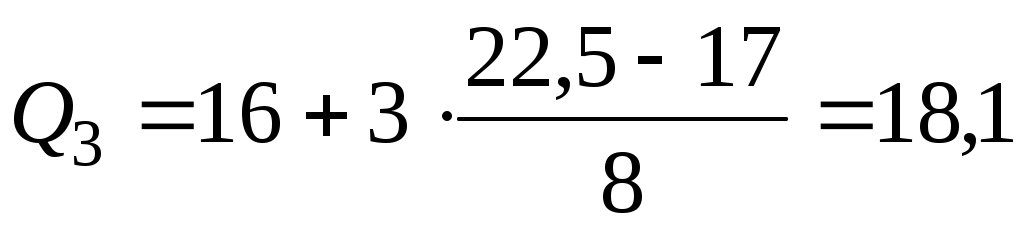 тыс.р. тыс.р.
Вывод. 25% сотрудников имеют заработную плату менее 11,75 тыс. р., и 25% сотрудников имеют заработную плату более 18,1 тыс. р., а остальные 50% сотрудников имеют заработную плату в пределах от 11,75 до 18,1 тыс. р.
4. Децили. Для расчета децилей необходимо определить интервалы, содержащие первый и девятый дециль. Интервал, содержащий первый дециль, имеет накопленную частоту, которая первая превышает  (т.е. 10% всей совокупности), (т.е. 10% всей совокупности),  . В графе накопленные частоты находим значение первое, превышающее 3,0. Это значение 4 соответствует интервалу 7–10, значит, этот интервал будет содержать первый дециль. . В графе накопленные частоты находим значение первое, превышающее 3,0. Это значение 4 соответствует интервалу 7–10, значит, этот интервал будет содержать первый дециль.
Интервал, содержащий первый дециль (7–10). Определим составляющие формулы:
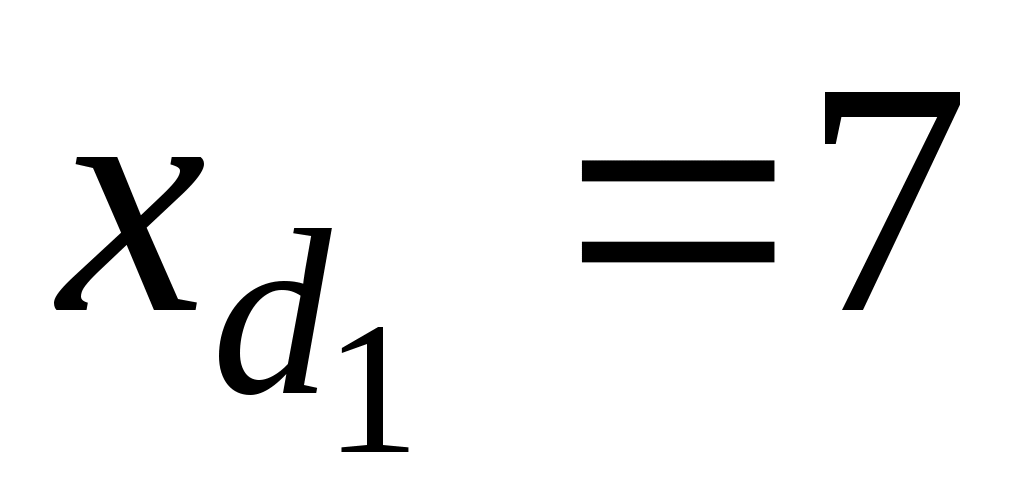 – нижняя граница интервала, содержащего первый дециль; – нижняя граница интервала, содержащего первый дециль;
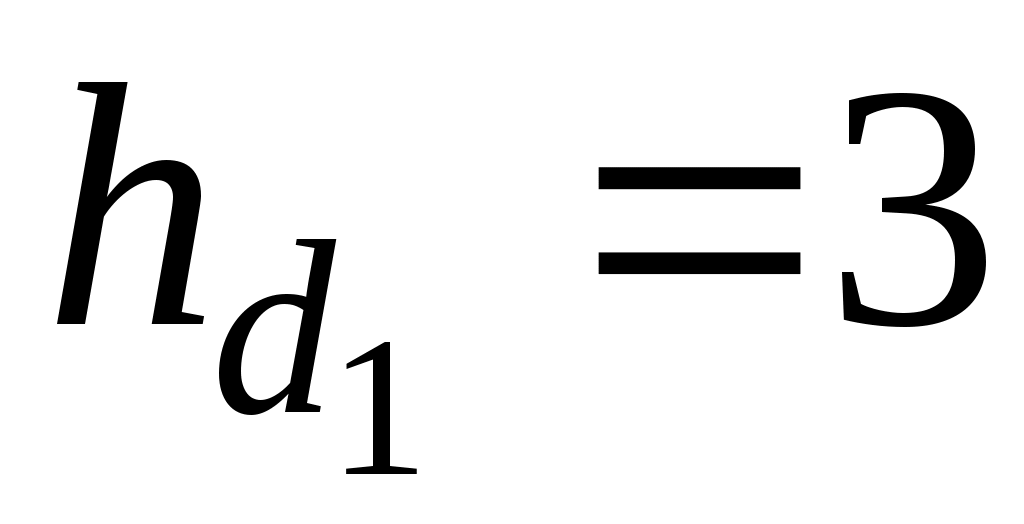 – величина интервала, содержащего первый дециль; – величина интервала, содержащего первый дециль;
 – сумма накопленных частот интервалов, предшествующих интервалу, содержащему первый дециль; – сумма накопленных частот интервалов, предшествующих интервалу, содержащему первый дециль;
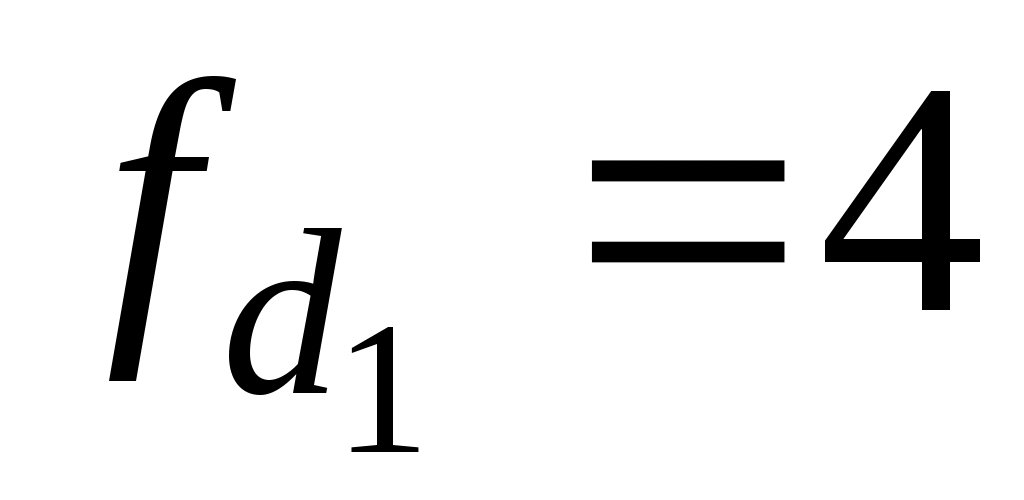 – частота интервала, содержащего первый дециль. – частота интервала, содержащего первый дециль.
Подставим все значения в формулу:
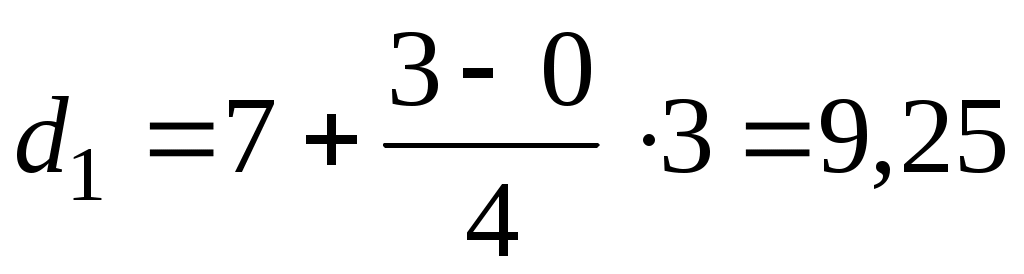 тыс.р. тыс.р.
Вывод. 10 % сотрудников имеют заработную плату менее 9,25 тыс. р., а 90 % сотрудников имеют заработную плату более 9,25 тыс. р.
Интервал, содержащий девятый дециль, имеет накопленную частоту, которая первая превышает  .В графе накопленные частоты находим значение первое, превышающее 27,0. Это число 28 соответствует интервалу 19–22, значит, этот интервал будет содержать девятый дециль. .В графе накопленные частоты находим значение первое, превышающее 27,0. Это число 28 соответствует интервалу 19–22, значит, этот интервал будет содержать девятый дециль.
Интервал, содержащий девятый дециль (19–22).Определим составляющие формулы:
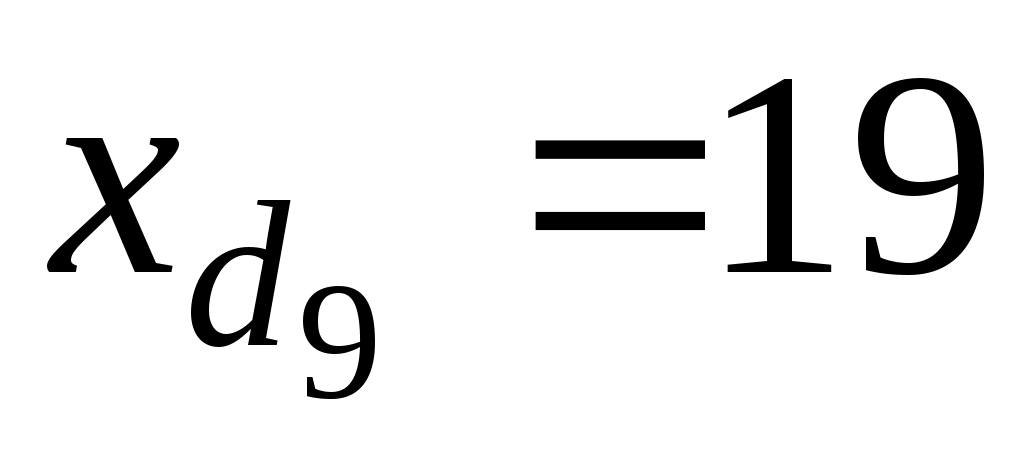 – нижняя граница интервала, содержащего девятый дециль; – нижняя граница интервала, содержащего девятый дециль;
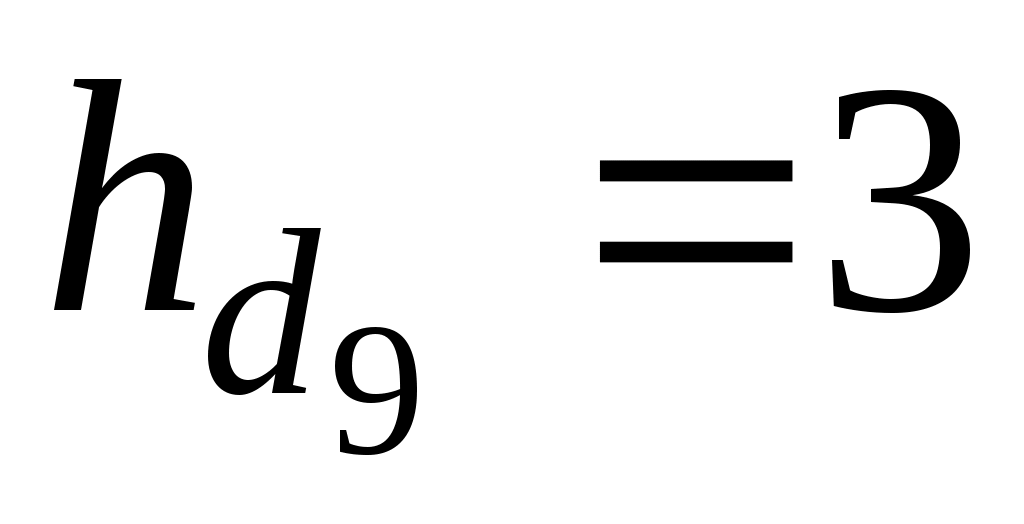 – величина интервала, содержащего девятый дециль; – величина интервала, содержащего девятый дециль;
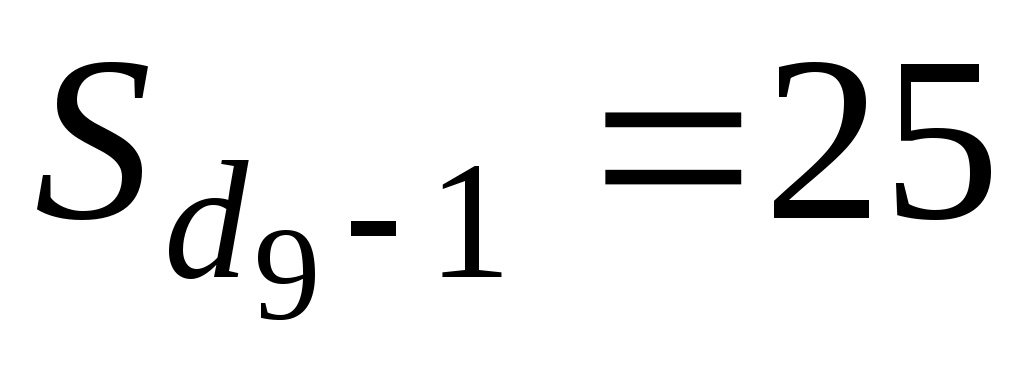 – сумма накопленных частот интервалов, предшествующих интервалу, содержащему девятый дециль; – сумма накопленных частот интервалов, предшествующих интервалу, содержащему девятый дециль;
 – частота интервала, содержащего девятый дециль. – частота интервала, содержащего девятый дециль.
Подставим все значения в формулу:
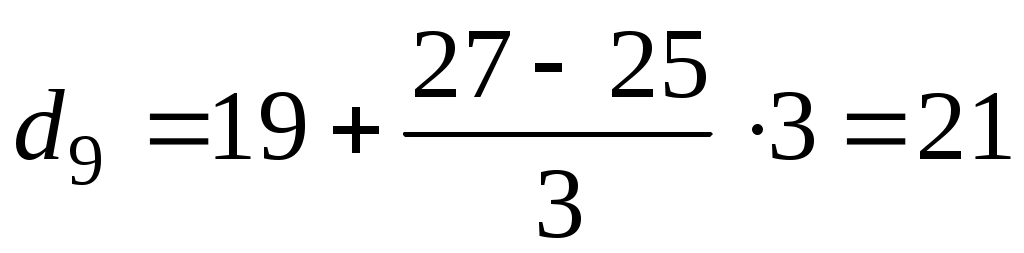 тыс.р. тыс.р.
Вывод. 90% сотрудников имеют заработную плату менее 21 тыс. р., а 10% сотрудников имеют заработную плату более 21 тыс. р.
 Вопросы и задания для самоконтроля Вопросы и задания для самоконтроля
Что такое относительная величина?
Какие виды относительных величин вам известны? Приведите примеры.
Что такое средняя величина?
Какие виды средних величин существуют?
Какие средние называются структурными? Как определить модальный интервал?
|
|
|
 Скачать 3.39 Mb.
Скачать 3.39 Mb.

 . (5.12)
. (5.12) , (5.13)
, (5.13)
 (5.14)
(5.14) (5.15)
(5.15) (5.16)
(5.16) (5.17)
(5.17) (5.18)
(5.18) ; (5.19)
; (5.19) (5.20)
(5.20) ; (5.21)
; (5.21) , (5.22)
, (5.22)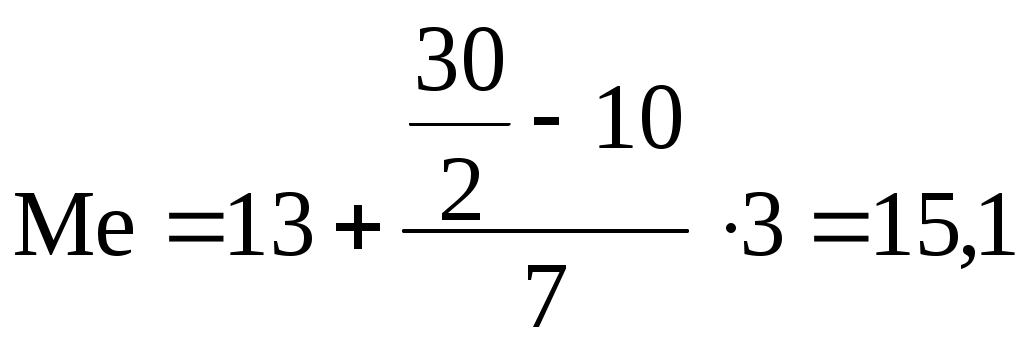 тыс.р.
тыс.р.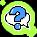 Вопросы и задания для самоконтроля
Вопросы и задания для самоконтроля
 (5.6)
(5.6) , (5.10)
, (5.10) ,
,