УП_Теория статистики_080200 испр.(. Томский политехнический университет н. В. Шаповалова, Н. В. Королева, Т. В. Громова теория статистикИ

• Название: Томский политехнический университет н. В. Шаповалова, Н. В. Королева, Т. В. Громова теория статистикИ
• Дата: 10.03.2023
• Размер: 3.39 Mb.
• Имя файла: УП_Теория статистики_080200 испр.(.doc
• Тип: Учебное пособие; #979637
• страница: 8 из 19

6.2. Вариация альтернативного признака

Альтернативный признак – качественный признак, имеющий две взаимоисключающие разновидности (например, работники предприятия подразделяются на мужчин и женщин; продукция – на годную и бракованную и т.д.).

Альтернативный признак принимает всего два значения: наличие признака и отсутствие признака:

(6.16)

где p – доли единиц, обладающих признаком;

q – доли единиц, не обладающих признаком.

Среднее значение альтернативного признака

(6.17)

Дисперсия альтернативного признака определяется по формуле

(6.18)

Например, если на 10 тыс. чел. населения района приходится 4тыс. мужчин и 6 тыс. женщин, то

; q=

Дисперсия альтернативного признака

.

Предельное значение дисперсии альтернативного признака равно 0,25. Оно получается при р=0,5.

6.3. Виды дисперсий и правило их сложения

Наряду с изучением вариации признака по всей совокупности вцелом бывает необходимо проследить количественные изменения признака по группам, на которые разделяется совокупность, а также между группами. Такое изучение вариации достигается посредством вычисления и анализа различных видов дисперсии.

Выделяют три вида дисперсий: общую, внутригрупповую и межгрупповую.

Общая дисперсия ( ) измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Общая дисперсия равна среднему квадрату отклонений отдельных значений признака от общей средней . Расчет общей дисперсии осуществляется по формуле:

<sub>. (6.19)

Общая дисперсия отражает вариацию признака за счет всех условий и причин, действующих в совокупности.</sub>

Внутригрупповая дисперсия ( ) равна среднему квадрату отклонений отдельных значений признака внутри группы от средней арифметической этой группы (групповой средней). Внутригрупповая дисперсия рассчитывается по каждой выделенной j-й группе по формуле:

, (6.20)

где – i-е значение признака в j-й группе;

– число единиц совокупности в j-й группе, обладающих i-м значением признака;

– среднее значение признака в j-й группе.

Эта дисперсия отражает вариацию признака только за счет условий и причин, действующих внутри группы.

Для всех групп в целом вычисляется средняя из внутригрупповых дисперсий ( ) как средняя арифметическая взвешенная величина:

, (6.21)

где – число единиц в j-й группе ( ).

Средняя из внутригрупповых дисперсий характеризует случайную вариацию, возникающую под влиянием других, неучтенных факторов, и не зависит от условия (признака-фактора), положенного в основу группировки.

Межгрупповая дисперсия ( ) равна среднему квадрату отклонений групповых средних от общей средней :

. (6.22)

Межгрупповая дисперсия характеризует вариацию значений исследуемого признака за счет действия на него только группировочного признака.

Указанные дисперсии взаимосвязаны между собой следующим равенством: величина общей дисперсии равна сумме средней из внутригрупповых дисперсий и межгрупповой дисперсии:

. (6.23)

Это тождество отражает закон сложения дисперсий. Из этого правила следует, что зная два вида дисперсий, всегда можно определить третий вид.

На основе этого правила рассчитывают эмпирические показатели тесноты корреляционной связи между факторными и результативными признаками.

Поскольку на величину межгрупповой дисперсии оказывает влияние только факторный признак, а на величину общей дисперсии, помимо факторного признака, и все остальные признаки, то частное от деления первой дисперсии на вторую укажет на силу влияния факторного признака на результативный.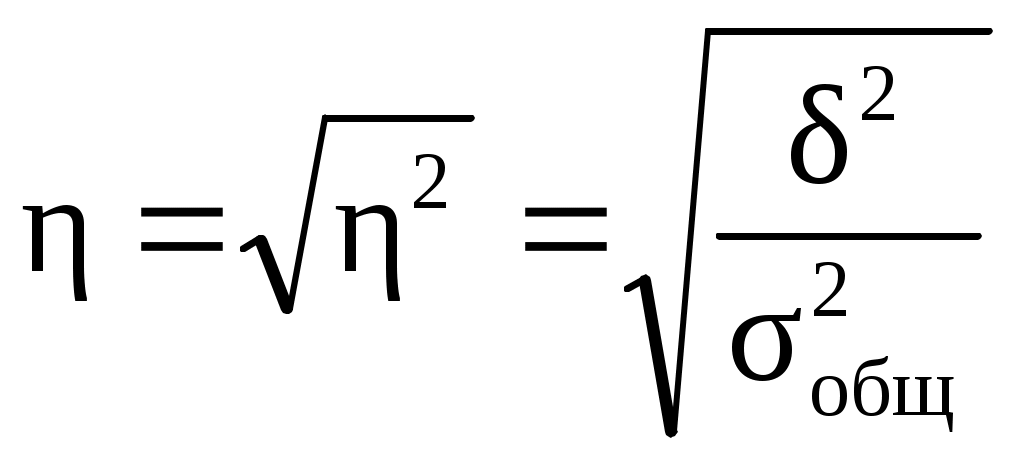

Эмпирический коэффициент детерминации ( ) характеризует долю межгрупповой дисперсии в общей дисперсии и рассчитывается по формуле:

. (6.24)

Эмпирическое корреляционное отношение представляет собой корень квадратный из эмпирического коэффициента детерминации и рассчитывается следующим образом:

. (6.25)

С помощью данного показателя можно оценить тесноту связи между группировочным (факторным) и результативным признаками.

Значение данного коэффициента изменяется в пределах [0;1]. Чем ближе к 1 будет величина η, тем сильнее взаимосвязь между рассматриваемыми признаками. Если η=0, то группировочный признак не оказывает влияния на результативный, если η=1, то результативный признак изменяется только в зависимости от признака, положенного в основание группировки, а влияние прочих факторных признаков равно нулю. Промежуточные значения оцениваются в зависимости от их близости к предельным значениям.

Пример 6. В результате обследования работы банков получено следующее распределение по доходности активов, представленное в таблице 10.

Таблица 10

Распределение банков по доходности активов

Группа банков	Доходность, %	Число банков
С низким уровнем информационных технологий (IT)	10–15	10
	15–20	15
	20–25	20
С высоким уровнем информационных технологий (IT)	25–30	40
	30–35	10
	35–40	5

Рассчитайте внутригрупповые дисперсии, среднюю из внутригрупповых дисперсий, межгрупповую дисперсию и общую дисперсию (по правилу сложения дисперсий). Вычислите эмпирическое корреляционное отношение.

Решение. В данном примере выделено две группы: с низким уровнем IT и высоким уровнем IT.

Ниже представим расчет показателей.

Представим промежуточные результаты в таблице11 для каждой группы.

Таблица 11

Группа банков	Доходность, %	Число банков,
С низким уровнем информационных технологий (IT)	10–15	10	12,5	125
	15–20	15	17,5	262,5
	20–25	20	22,5	450
ИТОГО:	-	45	-	837,5
С высоким уровнем информационных технологий (IT)	25–30	40	27,5	1100
	30–35	10	32,5	325
	35–40	5	37,5	187,5
ИТОГО:	-	55	-	1612,5

• 
  Среднюю доходность для каждой группы банков определим по формуле средней арифметической взвешенной:
  

• 
  для банков с низким уровнем IT:
  

;

• 
  для банков с высоким уровнем IT:
  

.

• 
  Рассчитаем внутригрупповые дисперсии для каждой из групп по формуле (6.20):
  

• 
  для банков с низким уровнем IT:
  

• 
  для банков с высоким уровнем IT:
  

• 
  Средняя из внутригрупповых дисперсий определяется по формуле (6.21):
  

.

• 
  Для расчета межгрупповой дисперсии необходимо предварительно определить общую среднюю для совокупности как среднюю из внутригрупповых средних:
  

.

• 
  Теперь можем рассчитать межгрупповую дисперсию по формуле (6.22):
  

.

• 
  Определим общую дисперсию по правилу сложения дисперсий, для этого используем формулу (6.23):
  

.

Рассмотрим, в какой мере группировочный признак (уровень информационных технологий) оказывает влияние на вариацию доходности у банков, и оценим степень их взаимосвязи. Для этого вычислим эмпирический коэффициент детерминации и эмпирическое корреляционное отношение по формулам (6.24 и 6.25):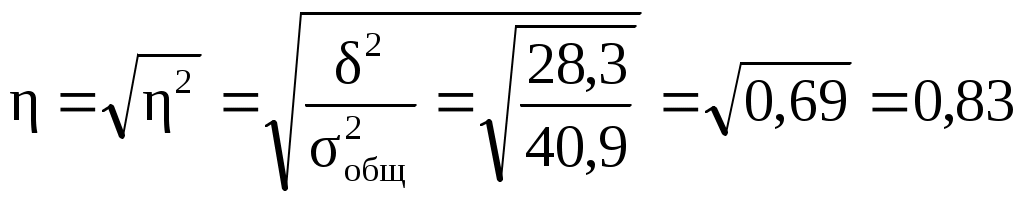

или 69%,

или 83%.

Полученное значение эмпирического коэффициента детерменации означает, что доходность банков на 69% зависит от уровня информационных технологий и соответственно на 31% от других факторов.

Степень близости к 1 значения эмпирического корреляционного отношения позволяет утверждать, что существует достаточно тесная связь между доходностью банков и уровнем IT.

Проведенный анализ позволяет сделать вывод, что доходность банков во многом зависит от их уровня информационных технологий.