УП_Теория статистики_080200 испр.(. Томский политехнический университет н. В. Шаповалова, Н. В. Королева, Т. В. Громова теория статистикИ

• Название: Томский политехнический университет н. В. Шаповалова, Н. В. Королева, Т. В. Громова теория статистикИ
• Дата: 10.03.2023
• Размер: 3.39 Mb.
• Имя файла: УП_Теория статистики_080200 испр.(.doc
• Тип: Учебное пособие; #979637
• страница: 10 из 19

Проверь себя

Выберите правильный вариант ответа.

1.Вариация – это…

а) изменяемость величины признака у отдельных единиц совокупности;

б) изменение структуры статистической совокупности во времени;

в) изменение состава совокупности.

2. Наилучшей характеристикой для сравнения вариации различных совокупностей служит:

а) размах вариации;

б) дисперсия;

в) среднее квадратическое отклонение;

г) коэффициент вариации.

3. Коэффициент вариации характеризует:

а) степень вариации признака;

б) тесноту связей между признаками;

в) типичность средней;

г) пределы колеблемости признака.

4. Дисперсия представляет собой:

а) средней размер отклонений индивидуальных значений признака от средней;

б) средний квадрат отклонений индивидуальных значений признака от средней арифметической;

в) средний квадрат отклонений индивидуальных значений признака от средней квадратической.

5.Величина дисперсии альтернативного признака существует в интервале:

а) 0,0–0,25;

б) 0,0–0,50;

в) 0,0–1,0.

6. Коэффициент асимметрии – это характеристика:

а) структуры вариационного ряда;

б) размера вариации;

в) формы вариации.

7. Для ассиметричных распределений коэффициент эксцесса (Ek>0) показывает:

а) островершинное распределение;

б) плосковершинное распределение;

в) нормальное распределение;

г) левостороннее распределение.

Глава 7
Выборочное наблюдение

7.1. Сущность и значение выборочного наблюдения,
его основные характеристики

Выборочное наблюдение – один из наиболее широко применяемых видов несплошного наблюдения. Это такое несплошное наблюдение, при котором статистическому обследованию (наблюдению) подвергается часть единиц совокупности, отобранных на основе научно разработанных принципов, обеспечивающих получение объективных обобщающих показателей для характеристики всей совокупности в целом.

Сущность выборочного наблюдения состоит в том, что обследованию подвергается часть совокупности, отобранная по особым правилам. Повышенное внимание к выборочному наблюдению в настоящее время связано с необходимостью более оперативного реагирования на происходящие изменения, принятия своевременных решений, что особенно важно в условиях рынка.

Выборочный метод является важнейшим источником информации в маркетинговых и социологических исследованиях, в контроле качества продукции; разработаны методологические подходы к применению выборочного наблюдения в аудите.

Преимущество выборочного наблюдения заключается в существенной экономии различного вида ресурсов, а именно:

• 
  финансовых средств, затрачиваемых на сбор и обработку данных, подготовку и оплату кадров;
  
• 
  материально-технических ресурсов (канцелярские товары, оргтехника, расходные материалы, транспортное обслуживание и т.п.);
  
• 
  трудовых ресурсов, привлекаемых к обследованию на всех его этапах;
  
• 
  времени, затрачиваемого как на получение первичной информации, так и на последующую ее обработку, вплоть до публикации итоговых материалов.
  

В то же время, необходимо четко представлять, что выборочное наблюдение, как бы грамотно с методологической точки зрения оно ни было организовано, всегда связано с определенными, пусть небольшими и измеряемыми ошибками. Поэтому, когда вариация регистрируемых признаков очень сильная и процент отбора для получения выборочных значений с заданной точностью достигает 20–25%, следует правильно оценить целесообразность несплошного обследования, сопоставив достаточно большие затраты всех ресурсов на такую объемную выборку и ожидаемые погрешности статистических характеристик. Кроме того, проведение выборки требует привлечения высококвалифицированного персонала, что, в свою очередь, ведет к увеличению стоимости обследования.

При решении ряда задач выборочное наблюдение является единственно возможным способом получения необходимой информации. Так, контроль многих видов продукции связан с их порчей, потерей товарного вида, нарушением герметизации и т.п. Например, нельзя проверить каждую производимую предприятием электролампу на соблюдение требований по продолжительности горения. Нельзя проверить на соответствие стандартам каждого пакета с соком или молочной продукцией, т.к. это связано с вскрытием их упаковки. В подобных случаях контроль качества может осуществляться только с использованием выборочного метода.

Реализация выборочного метода базируется на понятиях генеральной и выборочной совокупностей.

Генеральная совокупность – это вся исходная изучаемая статистическая совокупность, из которой на основе отбора единиц или групп единиц формируется совокупность выборочная. Поэтому генеральную совокупность также называют основой выборки.

Основные характеристики параметров генеральной и выборочной совокупности приведены в табл. 14.

Цель выборочного наблюдения – определение параметров генеральной совокупности на основе параметров выборочной совокупности. Разница между генеральными и выборочными параметрами называется ошибкой выборки, или ошибкой репрезентативности. Формулы ее определения, разработанные теорией вероятностей и математической статистикой, дифференцированы в зависимости от видов и способов отбора.

Выделяют следующие этапы проведения выборочного наблюдения:

• 
  определение необходимого объема выборки и способа отбора;
  
• 
  проведение отбора;
  
• 
  обобщение данных наблюдения и расчет выборочных характеристик;
  
• 
  расчет ошибок выборки;
  
• 
  распространение выборочных характеристик на генеральную совокупность.
  

Таблица 14

Основные характеристики параметров генеральной и
выборочной совокупности

Характеристики	Генеральная совокупность	Выборочная совокупность
1. Объем совокупности (число единиц)	N	n
2. Число единиц, обладающих обследуемым признаком	M	m
3. Доля единиц, обладающих обследуемым признаком
4. Средний размер признака
5. Дисперсия количественного признака
6. Дисперсия доли

Главные условия выборки:

1. 
   каждая единица генеральной совокупности должна иметь равную возможность попадания в выборку (принцип случайного непредвзятого отбора);
   
2. 
   в выборочную совокупность должны пропасть представители всех групп, имеющихся в генеральной совокупности;
   
3. 
   выборочная совокупность должна полно и адекватно воспроизводить закономерности, присущие всей генеральной совокупности (принцип репрезентативности).
   

7.2. Виды, методы и способы выборочного наблюдения

В зависимости от состава и структуры генеральной совокупности различают виды, методы и способы выборочного наблюдения, которые представлены на рис. 21.

Выделяют следующие виды отбора единиц из генеральной совокупности (рис. 21):

Индивидуальный отбор – в выборку отбираются отдельные единицы.

Групповой отбор – в выборку попадают качественно однородные группы или серии изучаемых единиц.



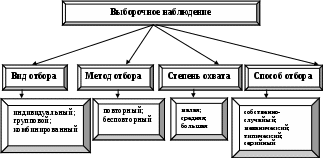
Рис. 21. Виды, методы и способы выборочного наблюдения

Комбинированный отбор – комбинация первых двух способов.

Чтобы выборка полно и адекватно представляла свойства генеральной совокупности, она должна быть представительной, или репрезентативной. Репрезентативность обеспечивается только при объективности отбора данных.

Различают два метода выборочного наблюдения: повторный и бесповторный отбор.

При повторном отборе вероятность попадания каждой отдельной единицы в выборку остается постоянной, т.к. после отбора отобранная единица возвращается в совокупность и снова может быть выбранной – «схема возвратного шара».

При бесповторном отборе отобранная единица не возвращается обратно, вероятность попадания остающихся единиц в выборку все время меняется – «схема безвозвратного шара».

Способ отбора определяет конкретный механизм или процедура выборки единиц из генеральной совокупности. В практике выборочного обследования наибольшее распространение получили следующие выборки:

• 
  собственно-случайная выборка;
  
• 
  механическая выборка;
  
• 
  типическая выборка;
  
• 
  серийная выборка.
  

7.3. Ошибки выборочного наблюдения

Одна из задач, решаемых на основе выборочного метода, – определение ошибки выборки (рис. 22). В статистике принято определять среднюю, предельную и относительную ошибки выборочного наблюдения.


Рис. 22. Виды ошибок при выборочном наблюдении

Ошибки регистрации могут иметь случайный или систематический характер, но их можно избежать при правильных организации и проведении наблюдения. Среди ошибок регистрации выделяют:

Систематические ошибки, зависящие от организации выборочного исследования и обусловленные причинами, действующими в каком-то одном направлении и искажающими результаты работы (например, округление цифр, тяготение к полным десяткам, сотням и т.д.).

Случайные ошибки, связанные с природой любых статистических погрешностей и проявляющиеся в различных направлениях, уравновешивающие друг друга и лишь изредка дающие заметный суммарный итог.

Ошибка выборочного наблюдения (репрезентативности) – расхождение между характеристиками выборки и генеральной совокупности. Она зависит от численности выборки, вариации признака, методов отбора единиц выборочной совокупности и т.д.

Предельная ошибка выборки – величина случайная. Наиболее полно закономерности случайных ошибок выборки раскрыты в теоремах П.Л. Чебышева и А.М. Ляпунова.

Теорему П.Л. Чебышева можно сформулировать следующим образом: при достаточно большом числе независимых наблюдений можно с вероятностью, близкой к единице (т.е. почти с достоверностью), утверждать, что отклонение выборочной средней от генеральной будет сколько угодно малым. В теореме П.Л. Чебышева доказано, что величина ошибки не должна превышать . Она зависит от коэффициента доверия и средней ошибки выборки:

, (7.1)

где Δ – предельная ошибка выборки;

t – коэффициент доверия, зависящий от вероятности, с которой определяется предельная ошибка выборки;

– средняя ошибка выборки, которая зависит от способа производства выборки.

Теорема А.М. Ляпунова доказывает, что распределение выборочных средних, а следовательно и их отклонений от генеральной средней, при достаточно большом числе независимых наблюдений, приближенно нормально при условии, что генеральная совокупность обладает конечной средней и ограниченной дисперсией.

Математически теорему Ляпунова можно записать так:

;



где Ф(t) =P – интеграл Лапласа, для которого имеются справочные таблицы в литературе по математической статистике;

– математическая постоянная.

Значения коэффициента доверия t находят по специальным таблицам, в зависимости от требуемой вероятности. В частности, при:



Поскольку t указывает на вероятность расхождения , т.е. на вероятность того, на какую величину генеральная средняя будет отличаться от выборочной средней, то это может быть прочитано так: с вероятностью 0,683 можно утверждать, что разность между выборочной и генеральной средними не превышает одной величины средней ошибки выборки. Другими словами, в 68,3% случаев ошибка репрезентативности не выйдет за пределы . С вероятностью 0,954 можно утверждать, что ошибка репрезентативности не превышает (т.е. в 95% случаев). С вероятностью 0,997, т.е. довольно близкой к единице, можно ожидать, что разность между выборочной и генеральной средней не превзойдет трехкратной средней ошибки выборки и т.д.

Результаты выборочного наблюдения переносятся на генеральную совокупность следующим образом:

• 
  для средней
  

; (7.2)

• 
  для доли
  

. (7.3)

Таким образом, чем больше коэффициент доверия, т.е. чем выше требуемая точность, тем больше интервал, куда с определенной вероятностью попадет искомое значение параметра генеральной совокупности.

Относительная ошибка выборки рассчитывается по формулам:

а) для средней:

; (7.4)

б) для доли:

. (7.5)

При <25% выборка репрезентативна для оценки и расчета средних показателей по совокупности.

При <25% выборка репрезентативна для оценки доли.

При и > 25% можно сделать вывод о нерепрезентативности выборки.

7.4. Способы отбора при выборочном наблюдении

В практике выборочных обследований наибольшее распространение получили следующие виды выборок:

Собственно-случайная выборка. Собственно-случайная выборка – отбор единиц из генеральной совокупности в целом, без разделения ее на группы, подгруппы или серии отдельных единиц. При этом единицы отбираются в случайном порядке, не зависящем ни от последовательности расположения единиц в совокупности, ни от значений их признаков.

Прежде чем производить собственно-случайный отбор, необходимо убедиться, что все без исключения единицы генеральной совокупности имеют абсолютные шансы попадания в выборку, в списках или перечне отсутствуют пропуски, нет игнорирования отдельных единиц и т.п. Следует также установить четкие границы генеральной совокупности таким образом, чтобы включение или невключение в нее отдельных единиц не вызывало сомнений.

Собственно – случайный отбор может быть как повторным, так и бесповторным. После проведения отбора для определения возможных границ генеральных характеристик рассчитываются средняя и предельная ошибки выборки.

Таблица 15

Формулы для расчета ошибок собственно-случайной выборки

Средняя ошибка выборки μ	Метод отбора
	повторный	бесповторный
Для средней
Для доли

Здесь – выборочная (или генеральная) дисперсия; – выборочное (или генеральное) среднее квадратическое отклонение; – объем выборочной совокупности; – объем генеральной совокупности.

Пример 9. В результате выборочного обследования доходов домохозяйств региона, осуществленного на основе собственно-случайной повторной выборки, получен следующий ряд распределения (табл. 16):
Таблица 16

Результаты выборочного обследования
доходов домохозяйств региона

Доход, тыс.р.	До 5	5–10	10–15	15–20	20 и более
Число домохозяйств	52	150	194	170	98

С вероятностью 0,954 определите границы среднего дохода домохозяйств в целом по данному региону, опираясь только на результаты выборочного обследования.

Решение. Для того чтобы определить границы среднего дохода домохозяйств по данному региону, воспользуемся формулой (7.2):

.

Необходимо определить предельную ошибку выборки, для этого воспользуемся формулой:

, или

Чтобы определить границы, нам необходимо найти дисперсию по формуле 6.5.

Для расчёта дисперсии необходимо рассчитать выборочную среднюю. Для этого воспользуемся формулой средней арифметической взвешенной. Промежуточные расчеты сведем в табл. 17.

Выборочная средняя:

тыс. р.

Таблица 17

Доход, тыс. р.	Число домохозяйств	Середина интервала
До 5	52	2,5	130	6065,28
5–10	150	7,5	1125	5046
10–15	194	12,5	2425	124,16
15–20	170	17,5	2975	2998,8
20 и более	98	22,5	2205	8294,72
Итого	664	-	8860	22528,96

Рассчитываем дисперсию:

тыс. р.

Подставим все полученные значения в формулу для нахождения предельной ошибки выборки:

тыс. р.

Установим границы генеральной средней с учетом полученных значений:

.

Вывод. Таким образом, на основании проведенного выборочного обследования с вероятностью 0,954 мы можем утверждать, что средний доход домохозяйства в целом по региону лежит в пределах от 12,85 до 13,75 тыс. р.

Механическая (систематическая) выборка. Механическая выборка может быть применена в тех случаях, когда генеральная совокупность каким–либо образом упорядочена, т.е. имеется определенная последовательность в расположении единиц (табельные номера работников, списки избирателей, телефонные номера респондентов, номера домов и квартир и т.п.). Для проведения отбора желательно, чтобы все единицы также имели порядковые номера от 1 до n.

Для проведения механической выборки устанавливается пропорция отбора, которая определяется соотнесением объемов выборочной и генеральной совокупностей. Так, если из совокупности в 500000 единиц предполагается отобрать 10000 единиц, то пропорция отбора составит . Отбор единиц осуществляется в соответствии с установленной пропорцией через равные интервалы.

Интервал отбора также можно определить как частное от деления 100% на установленный процент отбора. В тех случаях, когда результат деления получается дробным, сформировать выборку механическим способом при строгом соблюдении процента отбора не представляется возможным.

Генеральную совокупность при механическом отборе можно ранжировать или упорядочить по величине изучаемого или коррелирующего с ним признака, что позволит повысить репрезентативность выборки. Однако в этом случае возрастает опасность систематической ошибки, связанной с занижением значений изучаемого признака (если из каждого интервала регистрируется первое значение) или его завышением (если из каждого интервала регистрируется последнее значение). Поэтому целесообразно из каждого интервала отбирать центральную или одну из двух центральных единиц. При этом порядковый номер единицы, с которой начинается отбор, определяется следующим образом: если интервал отбора обозначить как , то номер первой отбираемой единицы будет:

• 
  при – нечетном
  

;

• 
  при – четном
  

, или .

Опасность систематической ошибки при механической выборке также может появиться вследствие случайного совпадения выбранного интервала и циклических закономерностей в расположении единиц генеральной совокупности.

Для определения средней ошибки механической выборки, а также необходимой ее численности используются соответствующие формулы, применяемые при собственно-случайном бесповторном отборе. При этом, определив необходимую численность выборки и сопоставив ее с объемом генеральной совокупности, как правило, приходится производить соответствующее округление для получения целочисленного интервала отбора.

Типическая (стратифицированная) выборка. Типический отбор целесообразно использовать в тех случаях, когда все единицы генеральной совокупности объединены в несколько крупных типических групп. Такие группы также называют стратами, или слоями, в связи с чем типический отбор также называют стратифицированным, или расслоенным. При обследовании населения в качестве типических групп могут быть выбраны области, районы, социальные, возрастные или образовательные группы; при обследовании предприятий – отрасли или подотрасли, формы собственности и т.п.

Рассматривать генеральную совокупность в разрезе нескольких крупных групп единиц имеет смысл только в том случае, если средние значения изучаемых признаков по группам существенно различаются. Например, с большой уверенностью можно предположить, что доходы населения крупного города будут в среднем выше доходов населения, проживающего в сельской местности; численность работников промышленного предприятия в среднем будет выше численности работников торгового или сельскохозяйственного предприятия; средний возраст студентов будет значительно ниже среднего возраста занятого населения, и тем более пенсионеров. В то же время, нет никакого смысла при выделении типических групп ориентироваться на признак, не связанный или очень слабо связанный с изучаемым. Например, при изучении доходов населения вряд ли улучшению результатов выборочного обследования будет способствовать деление населения на группы на основе первой буквы фамилии, т. к. маловероятно, что доходы людей, чья фамилия начинается с букв в интервале от А до К, будут существенно выше или ниже доходов лиц, носящих фамилию, начинающуюся с букв в интервале от Л до Я.

Отбор единиц в выборочную совокупность из каждой типической группы осуществляется собственно-случайным или механическим способом. Поскольку в выборочную совокупность в той или иной пропорции обязательно попадают представители всех групп, типизация генеральной совокупности позволяет исключить влияние межгрупповой дисперсии на среднюю ошибку выборки. В то же время, в выделенных типических группах обследуются далеко не все единицы, а только включенные в выборку. Следовательно, на величину полученной ошибки будет влиять различие между единицами внутри этих групп, т.е. внутригрупповая вариация. Поэтому ошибка типической выборки будет определяться величиной не общей дисперсии, а только ее части – средней из внутригрупповых дисперсий.

При выборке пропорционально объему типических групп число единиц, подлежащих отбору из каждой группы, определяется по формуле

, (7.6)

где – общее число единиц i-й типической группы;

– объем выборки из i-й типической группы.

При выборке, пропорциональной дифференциации признака, число наблюдений по каждой группе рассчитывается по формуле

, (7.7)

где – среднее квадратическое отклонение значений признака в i-й типической группе.

Таблица 18

Формулы для расчета ошибок при типической выборке

Средняя ошибка выборки μ	Метод отбора
	повторный	бесповторный
Для средней
Для доли

Пример 10. Для определения среднего возраста женщин, вступающих в брак, в городе была произведена 10%-я типическая пропорциональная выборка. Результаты обследования представлены в табл. 19.

Таблица 19

Социальная группа	Объем выборки, тыс. чел.	Доля женщин, вступающих во второй брак, %
Рабочие	35	8
Служащие	115	16

С вероятностью 0,997 установите границы доли женщин, второй раз вступающих в брак.

Решение. Долю женщин, вступающих во второй брак, необходимо определить по формуле (7.3):

.

Выборочную долю определим по формуле

или 14%.

Выборочную дисперсию альтернативного признака определим по формуле:

.

Средняя ошибка выборочной доли при типической выборки определяется по формуле:



Предельную ошибку определим по формуле с вероятность 0,997 (t=3) (7.2):

или 8%.

Установим границы генеральной доли с учетом полученных значений:

;

;



Вывод: Таким образом, с вероятностью 0,997 можно утверждать, что доля женщин, вступающих во второй брак, будет находиться в пределах от 6 до 22%.

Серийная выборка. Сущность серийной выборки заключается в собственно-случайном либо механическом отборе групп единиц (серий), внутри которых производится сплошное обследование. Данный способ отбора удобен в тех случаях, когда единицы генеральной совокупности изначально объединены в небольшие, более или менее равновеликие группы или серии. В качестве таких серий могут выступать упаковки с определенным количеством готовой продукции, партии товара, студенческие группы, бригады и другие подобные объединения.

В связи с тем, что при серийном отборе внутри отобранных групп обследуются все без исключения единицы, внутригрупповая вариация признака не отразится на ошибках выборочного наблюдения. В то же время, обследуются не все группы, а только попавшие в выборку. Следовательно, на ошибках получаемых характеристик отразятся различия между группами, которые определяются межгрупповой дисперсией.

Формулы для расчета средней ошибки выборки при серийном отборе представлены в табл. 20.

Таблица 20

Формулы для расчета ошибок при серийной выборке

Средняя ошибка выборки μ	Метод отбора
	повторный	бесповторный
Для средней
Для доли

Здесь R – число серий в генеральной совокупности; r – число отобранных серий.
Пример 11. В области, состоящей из 20 районов, проводилось выборочное обследование урожайности зерновых на основе отбора серий (районов). Выборочные средние по районам составили соответственно 16; 17,5; 19; 18; 15 ц/га. С вероятностью 0,954 найдите пределы урожайности во всей области.
Решение. Для того чтобы определить среднее отклонение параметров в совокупности в целом, необходимо определить предельную ошибку выборки.

Для этого рассчитаем выборочную среднюю по формуле средней арифметической простой:

ц/га.

Межгрупповая (межсерийная) дисперсия



Определим предельную ошибку серийной бесповторной выборки:

ц/га.

Установим границы среднего отклонения по всей совокупности с учетом полученных значений (7.2):

.

Следовательно, урожайность в области с вероятностью 0,954 будет находиться в пределах

;
.

Вывод: Таким образом, средняя урожайность в районе находится в пределах от 15,3 до 18,9 ц/га.

7.5. Определение численности выборочной совокупности

Перед проведением выборочного наблюдения необходимо решить вопрос о том, сколько единиц из генеральной совокупности следует отобрать в выборочную совокупность. С увеличением объема выборки средняя ошибка выборочного наблюдения уменьшается, но, в то же время, увеличиваются затраты на проведение наблюдения. Количество единиц, отбираемое в выборку, будет зависеть также от коэффициента доверия и дисперсии изучаемого признака, а при бесповторной выборке – еще и от величины генеральной совокупности.

Приведем формулы необходимого объема выборки для наиболее часто используемых на практике способов формирования выборочной совокупности (табл. 21).

Расчет объема выборки при заданном уровне относительной ошибке выборки осуществляется по формулам

;

,

где v – коэффициент вариации;

Пример 12. С целью определения доли сотрудников коммерческих банков области, возраст которых старше 40 лет, предполагается организовать типическую выборку пропорционально численности сотрудников мужского и женского пола с механическим отбором внутри групп. Общее число сотрудников банков составляет 12 тыс. человек, в т.ч. 7 тыс. мужчин и 5 тыс. женщин. На основании предыдущих обследований известно, что средняя из внутригрупповых дисперсий составляет 1600.

Определите необходимый объем выборки при вероятности 0,997 (t=3) и ошибке 5 %.

Решение. Рассчитаем общую численность типической выборки (табл. 21):



Рассчитаем объем отдельных типических групп по формуле :





Вывод. Таким образом, необходимый объем выборочной совокупности сотрудников коммерческих банков составляет 550 человек, в т.ч. 321 – мужчины и 229 – женщины.

Таблица 21

Формулы расчета оптимальной численности выборки
при различных способах отбора

Способ отбора	Виды выборки
	Для средней		Для доли
	повторный	бесповторный	повторный	бесповторный
Собственно-случайный механический
Т ипический
Серийный

Пример 13. В районе города проживает 2200 семей. В случае случайной повторной выборки необходимо определить средний размер выборки при условии, что ошибка выборочной средней не превышает 0,8 семьи с вероятностью 0,954 и при среднем квадратическом отклонении 2 семьи.

Решение. В случае повторного случайного отбора необходимая численность выборки рассчитывается по формуле (табл. 21):



Вывод. Таким образом, необходимый объем выборочной совокупности составляет 25 семей района города.

Вопросы и задания для самоконтроля

1. 
   Дайте определение генеральной и выборочной совокупностям.
   
2. 
   Назовите виды и способы отбора единиц из генеральной совокупности.
   
3. 
   От чего зависит репрезентативность выборки?
   
4. 
   Как связаны между собой предельная и средняя ошибки выборки?
   
5. 
   Как определяется необходимая численность случайной выборки при заданной величине ошибки и доверительной вероятности?
   
6. 
   В чем преимущество выборочного наблюдения?
   
7. 
   В чем отличие механического отбора от собственно-случайного?