УП_Теория статистики_080200 испр.(. Томский политехнический университет н. В. Шаповалова, Н. В. Королева, Т. В. Громова теория статистикИ

• Название: Томский политехнический университет н. В. Шаповалова, Н. В. Королева, Т. В. Громова теория статистикИ
• Дата: 10.03.2023
• Размер: 3.39 Mb.
• Имя файла: УП_Теория статистики_080200 испр.(.doc
• Тип: Учебное пособие; #979637
• страница: 11 из 19

Проверь себя

Выберите правильный вариант ответа.

1. Генеральная совокупность – это совокупность…

а) единицы которой будут подвергнуты обследованию;

б) случайно попавшая в распоряжение исследования;

в) из которой проводится отбор единиц для непосредственного наблюдения.

2. Ошибки регистрации могут возникнуть:

а) только при выборочном наблюдении;

б) только при сплошном наблюдении;

в) при сплошном и несплошном наблюдении.

3. Расхождение между средними выборочной и генеральной совокупностями представляет собой:

а) объем выборки;

б) коэффициент доверия;

в) среднюю ошибку выборки;

г) предельную ошибку выборки.

4. Чтобы уменьшить ошибку выборки, рассчитанную в условиях механического отбора, можно:

а) уменьшить численность выборки;

б) увеличить численность выборки;

в) применить серийный отбор;

г) применить типический отбор.

5. Если отобранная единица совокупности может быть отобрана дважды, то такой отбор называется:

а) случайным;

б) бесповторным;

в) повторным.

6. При определении средней ошибки выборки для серийного отбора рассчитывается:

а) общая дисперсия;

б) межгрупповая дисперсия;

в) средняя из групповых дисперсий.

Глава 8
Статистическое изучение взаимосвязи
социально-экономических явлений

8.1. Классификация видов взаимосвязи

Исследование объективно существующих связей между социально-экономическими явлениями и процессами является важнейшей задачей теории статистики.

Изучение взаимосвязей на рынке товаров и услуг – важнейшая функция работников коммерческих служб: менеджеров, экономистов, коммерсантов. Особую актуальность изучение приобретает в условиях развивающейся рыночной экономики. Изучение механизма спроса и предложения, влияния объема и состава предложения товарных запасов, издержек обращения, прибыли и других качественных показателей имеет первостепенное значение для прогнозирования конъюнктуры рынка, рациональной организации торговых процессов и решения многих вопросов успешного ведения бизнеса.

Статистика призвана изучать закономерности с помощью особых методов, меняющихся в зависимости от характера исходной информации и целей познания. Знание характера и силы связей дает возможность управлять социально-экономическими процессами и предсказывать их развитие.

В процессе статистического исследования зависимостей вскрываются причинно-следственные отношения между явлениями, что позволяет выявить факторы (признаки), оказывающие существенное влияние на вариацию изучаемых явлений и процессов.

Причинно-следственные отношения – это связь явлений и процессов, при которой изменение одного из них – причины – ведет к изменению другого – следствия.

Причина – это совокупность условий, обстоятельств, действие которых приводит к появлению следствия.

Социально-экономические явления представляют собой результат одновременного воздействия большого числа причин. При изучении этих явлений необходимо выявлять главные, основные причины, абстрагируясь от второстепенных.

В основе первого этапа – статистического изучения связи – лежит качественный анализ изучаемого явления методами экономической теории, социологии и т.п.

Второй этап – построение модели. Он базируется на основе методов статистики: группировок, средних величин, таблиц и т.д.

Третий этап – интерпретация результатов; анализ вновь связан с качественными особенностями изучаемого явления.

Статистика разработала множество методов изучения связей, выбор которых зависит от целей исследования и поставленных задач.

Признаки по их сущности и значению для изучения взаимосвязей делятся на два класса.

Признаки, обусловливающие изменения других (связанных с ними) признаков, называются факторными (обозначаются через X).

Признаки, изменяющиеся под действием факторных признаков, называются результативными (обозначаются через Y).

Существует два основных типа связей между социально-экономическими явлениями: функциональная и статистическая (стохастическая) связь.

При функциональной связи каждому значению факторного признака соответствует одно и только одно значение результативного признака.

Связь между результативным и факторным признаком можно записать как



Примером функциональной связи при изучении физических явлений может служить зависимость расстояния, пройденного объектом, от скорости его движения. Примером функциональной зависимости при изучении экономических показателей могут являться плата за кредит, начисляемая на основе установленной процентной ставки; показатель доходности ценной бумаги, рассчитанной по математической формуле, а, следовательно, находящейся в функциональной зависимости от курса ценной бумаги.

Если причинная зависимость проявляется не в каждом отдельном случае, а в общем, среднем, при большом числе наблюдений, то такая зависимость называется статистической (стохастической).

Частным случаем стохастической является корреляционная связь, при которой изменение среднего значения результативного признака обусловлено изменением факторных признаков. Например, известно, что прибыль туристических фирм определенным образом связана с количеством клиентов. Тем не менее нельзя точно вычислить объем ожидаемой прибыли при заданном количестве клиентов, т.к. помимо клиентской базы, на прибыль могут влиять и множество других факторов, среди которых имеются и случайные. Их действие и приводит к стохастической зависимости. Таким образом, мы можем рассчитать лишь среднее значение прибыли, которое будет получено в целом по совокупности туристических фирм со схожим объемом клиентской базы.

Связи между явлениями и их признаками классифицируются по степени тесноты связи, направлению и аналитическому выражению (рис. 23).

Рис. 23. Классификация видов взаимосвязи
По степени тесноты связи различают количественные критерии оценки тесноты связи (табл. 22).

Таблица 22

Количественные критерии оценки тесноты связи

Величина коэффициента корреляции	Характер связи
До	практически отсутствует
–	слабая
–	умеренная
–	сильная

По направлению выделяют связь прямую и обратную.

Связь называется прямой, если с увеличением или уменьшением значений факторного признака происходит увеличение или уменьшение значений результативного признака. Например, рост объемов производства способствует увеличению прибыли предприятия.

В случае обратной связи значения результативного признака изменяются в противоположном направлении по сравнению с изменением факторного признака. Например, снижение себестоимости единицы производимой продукции влечет за собой рост прибыли.

По аналитическому выражению выделяют линейные и нелинейные связи.

Если статистическая связь между явлениями приближенно выражена уравнением прямой линии, то такую связь называют линейной; если же она выражена уравнением какой-либо кривой линии (параболы, гиперболы, показательной, экспоненциальной и т.д.), её называют
нелинейной, или криволинейной.

8.2. Методы изучения взаимосвязи
социально-экономических явлений

Для выявления наличия связи, ее характера и направления в статистике используются методы:

• 
  приведения параллельных данных;
  
• 
  аналитических группировок;
  
• 
  графический;
  
• 
  корреляционный анализ;
  
• 
  регрессионный анализ.
  

Метод приведения параллельных данных основан на сопоставлении двух или нескольких рядов статистических величин. Такое сопоставление позволяет установить наличие связи и получить представление о ее характере.

Графический метод. Взаимосвязь двух признаков изображается графически с помощью поля корреляции (диаграммы рассеивания).

Поле корреляции – это поле точек, на котором каждая точка представляет каждую единицу совокупности в пространстве двух измерений, соответствующих двум факторам:x и y.

При построении поля корреляции необходимо соблюдать следующие требования:

• 
  в системе координат на оси абсцисс откладываются значения факторного признака, а на оси ординат – значения результативного признака;
  
• 
  каждое пересечение линий, проводимых через эти оси, обозначается точкой.
  

При отсутствии тесных связей наблюдается беспорядочное расположение точек на графике. Чем сильнее связь между признаками, тем теснее будут группироваться точки вокруг определенной линии, выражающей форму связи. На рис. 24 представлено поле корреляции.


Рис. 24. Поле корреляции (диаграмма рассеивания)

Для социально-экономических явлений характерно, что наряду с существенными факторами, формирующими уровень результативного признака, на него оказывают воздействие многие другие неучтенные и случайные факторы. Это свидетельствует о том, что взаимосвязи явлений, которые изучает статистика, носят корреляционный характер и аналитически выражаются функцией вида

. (8.1)

Корреляционный метод имеет своей задачей количественное определение тесноты связи между двумя признаками (при парной связи) и между результативным и множеством факторных признаков (при многофакторной связи).

В статистике различают следующие виды зависимостей:

• 
  парная корреляция – связь между двумя признаками (результативным и факторным или двумя факторными);
  
• 
  частная корреляция – зависимость между результативным и одним факторным признаками при фиксированном значении других факторных признаков;
  
• 
  множественная корреляция – зависимость результативного и двух или более факторных признаков, включенных в исследование.
  

Теснота связи количественно выражается величиной коэффициентов корреляции. Величина коэффициента корреляции служит также оценкой соответствия уравнения регрессии выявленным причинно-следственным связям.

Регрессия тесно связана с корреляцией и позволяет исследовать аналитическое выражение взаимосвязи между признаками.

Регрессионный метод заключается в определении аналитического выражения связи, в котором изменение одной величины (называемой зависимой, или результативным признаком) обусловлено влиянием одной или нескольких независимых величин (факторов), а множество всех прочих факторов, также оказывающих влияние на зависимую величину, принимается за постоянные и средние значения. Регрессия может быть однофакторной (парной) и многофакторной (множественной).

8.3. Собственно-корреляционные параметрические
методы изучения связи

Измерение тесноты и направления связи является важной задачей изучения и количественного измерения взаимосвязи социально-экономических явлений. Оценка тесноты связи между признаками предполагает определение меры соответствия вариации результативного признака от одного (при изучении парных зависимостей) или
нескольких (множественных) факторов.

Линейный коэффициент корреляции был впервые введен в начале 1890-х гг. Пирсоном, Эджвортом и Велдоном.

Линейный коэффициент корреляции, обозначаемый r, характеризует тесноту и направление связи между двумя коррелируемыми признаками в случае наличия между ними линейной зависимости.

В теории разработаны и на практике применяются различные модификации формул для расчета данного коэффициента:

, (8.2)

где n – число наблюдений;

; , , , .

Если преобразовать формулу (8.2), то линейный коэффициент корреляции можно вычислить по формуле

, (8.3)

или

. (8.4)

формулы (8.3), (8.4) применяются при изучении совокупностей малого объема ( ). Числитель выражает взаимодействие двух переменных и определяет знак корреляции.

Линейный коэффициент корреляции изменяется в пределах от –1 до 1: . При этом интерпретацию выходных значений коэффициента корреляции можно представить в табл. 23.
Таблица 23

Оценка линейного коэффициента корреляции

Значение линейного коэффициента связи	Характер связи	Интерпретация связи
	Взаимосвязь отсутствует	–
	Прямая	С увеличением xувеличивается y
	Обратная	С увеличением x уменьшается y
	Функциональная	Каждому значению факторного признака строго соответствует одно значение результативного признака

После расчета линейного коэффициента корреляции следует проверить его значимость. В связи с тем, что исходные данные, по которым устанавливается взаимосвязь признаков, являются выборкой из некоторой генеральной совокупности, вычисленный коэффициент корреляции будет тоже выборочным. Следовательно, с его помощью можно осуществить связь, только исходя из информации, которую представляют выборочные единицы. Коэффициент корреляции будет показывать реальную связь, присущую всей исследуемой совокупности, только в том случае, если отобранные единицы хорошо отражают закономерность и структуру генеральной совокупности. С увеличением числа наблюдений повышается достоверность коэффициента корреляции.

Значимость линейного коэффициента корреляции проверяется на основе t-критерия Стьюдента. При этом выдвигается и проверяется гипотеза H₀ о равенстве коэффициента корреляции нулю: .

Расчетное значение критерия определяется по формуле

. (8.5)

Расчетное значение t-критерия сравнивается с его табличным, определяемым по таблице табулированных значений:

, (8.6)

где α – уровень значимости, который показывает вероятность принятия ошибочного решения;

– число степеней свободы, характеризует количество свободно варьируемых элементов совокупности.

Возможность присутствия ошибки связана с тем, что при исследовании взаимосвязи данные взяты не из всей совокупности, а только из ее части. Обычно α принимают значения 0,05; 0,02; 0,01 и 0,001.

Если расчетное значение , то это свидетельствует о значимости линейного коэффициента корреляции, а следовательно, может быть использовано для характеристики связи между изучаемыми признаками.

Если расчетное значение , то гипотеза о равенстве коэффициента корреляции нулю принимается с вероятностью α и он признается незначительным, а следовательно, не может быть использован для характеристики связи между изучаемыми признаками генеральной совокупности, т.к. единицы выборочной совокупности не отражают реальную структуру генеральной совокупности.

Достаточно часто при решении реальных экономических задач
необходимо оценить степень влияния на результативный признак не одного фактора, а некоторой совокупности факторов. Таким образом, исследователь сталкивается с множественным корреляционно-регрес-сионым анализом, основными целями которого являются:

• 
  описание и понимание взаимосвязи;
  
• 
  прогнозирование нового наблюдения на основании имеющейся совокупности данных;
  
• 
  регулирование и управление бизнес-процессами.
  

Для измерения тесноты связи при множественной корреляционной зависимости вычисляют множественный коэффициент корреляции. Множественный коэффициент рассчитывается при наличии линейной связи между результативным и несколькими факторными признаками. В случае оценки связи между результативным (y) и двумя факторными признаками (x₁) и (x₂) множественный коэффициент корреляции можно определить по формуле

, (8.7)

где r – парные коэффициенты корреляции.

Множественный коэффициент корреляции изменяется в пределах от 0 до 1 и по определению положителен: . Приближение коэффициента к единице свидетельствует о сильной зависимости между признаками.

8.4. Регрессионный анализ в изучении взаимосвязи
социально-экономических явлений

Парная регрессия характеризует связь между двумя признаками: результативным и факторным. Аналитически связь между ними описывается уравнениями:

• 
  прямой ; (8.8)
  

• 
  параболы ; (8.9)
  
• 
  гиперболы и т.д. (8.10)
  

Определить тип уравнения можно, исследуя зависимость графически. Однако существуют более общие указания, позволяющие выявить уравнения связи, не прибегая к графическому изображению. Если результативный и факторный признаки возрастают одинаково, примерно в арифметической прогрессии, то это свидетельствует о наличии линейной связи между ними, а при обратной связи – гиперболической. если результативный признак увеличивается в арифметической прогрессии, а факторный значительно быстрее, то используется параболическая или степенная функции.

Оценка параметров уравнения регрессии , ( – в уравнении параболы второго порядка) осуществляется методом наименьших квадратов (МНК). В основе МНК лежит предположение о независимости наблюдений исследуемой совокупности и нахождении параметров модели ( и ). В этом случае минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по уравнению регрессии:

.

рассмотрим в качестве функции параметров и , проведем математические преобразования (дифференцирование) и получим



Откуда система нормальных уравнений для нахождения параметров линейной парной регрессии методом наименьших квадратов примет следующий вид:

(8.11)

Если связь между признаками описывается уравнением параболы, то система нормальных уравнений для нахождения параметров регрессии методом наименьших квадратов имеет вид

(8.12)

В уравнениях регрессии параметр показывает усредненное влияние на результативный признак неучтенных (невыделенных для исследования) факторов; параметр (а в уравнении параболы и ) –
коэффициент регрессии – показывает, насколько изменяется в среднем значение результативного признака при изменении факторного на единицу его собственного измерения.

Пример 14. Составьте линейное уравнение регрессии зависимости финансового оборота и количества обслуженных туристов 10 туристических фирм за 2010 г. (данные представлены в табл. 24, данные условные). Определите параметры уравнения и проанализируйте их. Охарактеризуйте тесноту и направление связи между признаками.
Таблица 24

Показатели финансового оборота и количества
обслуженных клиентов туристических фирм за 2010 г.

№ п/п	Финансовый оборот, млн р.	Количество обслуженных туристов, тыс. чел.
1	270,0	53,4
2	235,0	50,5
3	186,0	20,0
4	138,6	22,6
5	138,4	27,9
6	107,8	30,0
7	106,9	41,5
8	97,2	10,6
9	96,0	22,8
10	88,0	23,4

Решение. Определим факторный и результативный признак:

• 
  в качестве факторного признака (изменяющегося) выберем количество обслуженных туристов;
  
• 
  за результативный признак (который изменяется под действием факторного) выберем финансовый оборот туристической фирмы.
  

На основе качественного анализа можем определить, что между финансовым оборотом и количеством обслуженных туристов существует прямая связь: с увеличением количества обслуженных туристов увеличивается финансовый оборот фирмы. Можно выявить зависимость с помощью построения корреляционного поля (рис. 25).



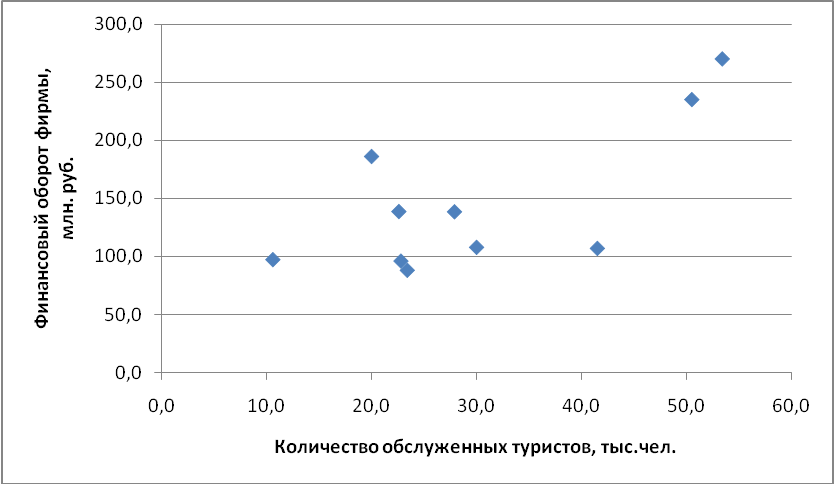
Рис. 25. Поле корреляции, характеризующее финансовый оборот
туристических фирм и количество обслуженных ими клиентов
Данная диаграмма рассеивания (поле корреляции) отображает линейную взаимосвязь между изучаемыми признаками, которую можно описать с помощью уравнения

.

Параметры уравнения определим при помощи решения системы нормальных уравнений по методу наименьших квадратов (МНК). Дополнительные расчеты представлены в табл. 25.

Используя данные дополнительных расчетов, составим систему уравнений



Решив систему уравнений, получим следующие значения параметров и :

; .

Таблица 25

№ п/п	Финансовый оборот , млн р.	Количество обслуженных туристов , тыс. чел.
1	270,0	53,4	14418,00	2851,56	221,72	72900
2	235,0	50,5	11867,50	2550,25	212,27	55225
3	186,0	20,0	3720,00	400,00	112,94	34596
4	138,6	22,6	3132,36	510,76	121,40	19209,96
5	138,4	27,9	3861,36	778,41	138,67	19154,56
6	107,8	30,0	3234,00	900,00	145,51	11620,84
7	106,9	41,5	4435,52	1722,25	182,96	11423,33
8	97,2	10,6	1030,32	112,36	82,32	9447,84
9	96,0	22,8	2188,34	519,84	122,05	9212,16
10	88,0	23,4	2059,20	547,56	124,01	7744
	1463,86	302,7	49946,60	10892,99	1463,84	250533,69

Тогда уравнение регрессии принимает вид

.

Свободный член уравнения характеризует величину финансового оборота туристических фирм, не зависящего от количества обслуженных туристов. Коэффициент регрессии показывает, что финансовый оборот, при увеличении количества клиентов у туристической фирмы на 1 тыс. чел., увеличится на 3,257 млн.р.

После того как составлено уравнение регрессии – на основе фактической информации по данным о 10 туристических фирмах за 2010 г.– рассчитаем теоретические значения путем подстановки в уравнение регрессии фактических данных о количестве обслуженных клиентов вместо значений :



и т.д. (табл. 25).

Для проверки правильности построения уравнения регрессии сумма значений эмпирического ряда должна совпадать с суммой вычисленных уровней выравненного ряда, т.е. .

В итоге получаем, что , что приблизительно равно , небольшую погрешность в вычислениях можно отнести на результаты округления.

Для определения тесноты связи между изучаемыми признаками необходимо вычислить линейный коэффициент корреляции. Для этого мы можем использовать формулу (8.3) или (8.4). Воспользуемся формулой (8.3) и дополнительными расчетами табл. 25:

.

Абсолютная величина линейного коэффициента корреляции свидетельствует о высокой тесноте связи между изучаемыми признаками, а знак «+» при коэффициенте – о том, что связь прямая. Другими словами, с увеличением количества обслуженных клиентов у туристической фирмы будет увеличиваться финансовый оборот данной фирмы.

Проверим полученный коэффициент корреляции на значимость:

;



Так как расчетное значение , то гипотеза H₀ равенства коэффициента корреляции нулю отвергается с вероятностью 95% (0,95), что свидетельствует о значимости линейного коэффициента корреляции, а следовательно и о подтверждении связи между финансовым оборотом и количеством обслуженных клиентов туристических фирм.

Основной смысл построенного уравнения регрессии – его практическая значимость и применение в целях планирования и прогнозирования экономических показателей. Поэтому если в данное уравнение регрессии вместо фактических данных о количестве обслуженных клиентов подставить планируемые показатели, то получим планируемый финансовый оборот. Таким образом, финансовый оборот планируется в зависимости от количества обслуженных туристов.

Допустим, что для первой туристической фирмы количество клиентов в следующем году увеличится и составит 55,0 тыс. чел. Рассчитаем величину финансового оборота у этой фирмы:

млн.р.

Допустим, для второй фирмы количество клиентов в следующем году уменьшится и составит 45,0 тыс. чел. Тогда величина финансового оборота у этой фирмы составит

млн.р.

Аналогичные прогнозные расчеты можно произвести и для других туристических фирм.

Вопросы и задания для самоконтроля

1. 
   Какие признаки называются факторными, а какие результативными?
   
2. 
   Какую связь между признаками называют функциональной?
   
3. 
   Что означает прямая и обратная связь между признаками?
   
4. 
   Что представляет собой корреляционно-регрессионый анализ?
   
5. 
   В чем сущность метода наименьших квадратов?
   
6. 
   Какой экономический смысл несут свободный член уравнения регрессии и коэффициент регрессии в линейном уравнении регрессии?
   
7. 
   В каких пределах изменяется линейный коэффициент корреляции? Что он показывает?