УП_Теория статистики_080200 испр.(. Томский политехнический университет н. В. Шаповалова, Н. В. Королева, Т. В. Громова теория статистикИ
 Скачать 3.39 Mb.
|
Проверь себяВыберите правильный вариант ответа. 1. Регрессионный анализ – это… а) количественное определение тесноты связи между признаками; б) измерение тесноты и направления связи и установление аналитического выражения связи; в) определение аналитического выражения связи между признаками; г) определение точности параметров связи. 2. Линейный коэффициент корреляции может принимать значения в пределах: а) от 0 до 1; б) от –1 до 1; в) от –1 до 0; г) любое значение. 3. Метод наименьших квадратов используется: а) для аналитического выражения связи; б) оценки параметров уравнения регрессии; в) количественной оценки тесноты и направления связи. 4. Чтобы определить, насколько изменится среднее значение результативного признака при изменении факторного на единицу собственной величины, необходимо: а) вычислить коэффициент корреляции; б) построить аналитическую группировку; в) вычислить параметры уравнения регрессии. 5. При какой связи направление изменения результативного признака совпадает с направлением изменения факторного признака: а) обратной; б) отрицательной; в) криволинейной; г) прямой. Глава 9 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Показатели | 2007 | 2008 | 2009 | 2010 | 2011 |
| 1. Число квартир, тыс. | 722 | 768 | 702 | 717 | 786 |
| 2. Средний размер квартир, м2 общей площади | 84,7 | 83,4 | 85,3 | 81,5 | 79,3 |
| 3. Удельный вес двухкомнатных квартир от общего объема, % | 32 | 32 | 31 | 32 | 31 |
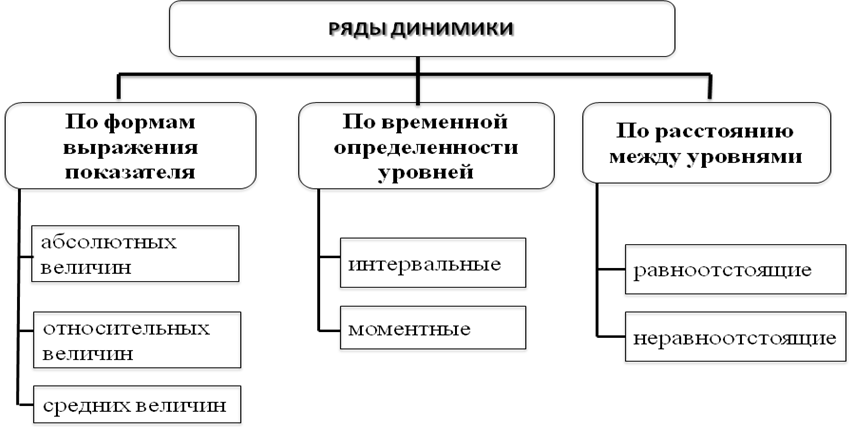
По временной определенности уровней ряды динамики классифицируются на моментные и интервальные.
Уровни моментного ряда динамики характеризуют явление по состоянию на определенный момент времени (на начало месяца, квартала, года и т.д.). Пример моментного ряда динамики представлен в табл. 27.Таблица 27
Численность населения в Российской Федерации
(на 1 января)
| Год | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
| Численность населения, млн. чел. | 144,2 | 143,5 | 142,8 | 142,2 | 142,0 | 141,9 | 141,9 |
Особенностью моментного ряда динамики является то, что в каждом последующем уровне содержится полностью или частично предыдущий уровень. Поэтому суммировать уровни моментного ряда не следует, т.к. это приведет к повторному счету.
Уровни интервального ряда динамики абсолютных величин характеризуют собой суммарный итог какого-либо явления за определенный отрезок времени (табл. 28). В отличие от моментных рядов сумма уровней интервального ряда является реальным показателем, например динамика браков и разводов в РФ за период с 2006–2010 гг.Таблица 28
Динамика браков и разводов населения в РФ, тыс.
| Годы | Браки | Разводы |
| 2006 | 1113,6 | 640,8 |
| 2007 | 1262,5 | 685,9 |
| 2008 | 1179,0 | 703,4 |
| 2009 | 1199,4 | 699,4 |
| 2010 | 1215,1 | 639,4 |
| ИТОГО | 5969,6 | 3368,9 |
Ряды динамики следующих друг за другом периодов или следующих через определенные промежутки дат называются равноотстоящими. Если же в рядах даются прерывающиеся периоды или неравномерные промежутки между датами, то ряды называются неравноотстоящими.Сопоставимость уровней рядов динамики
Важнейшим условием правильного построения ряда динамики является сопоставимость всех входящих в него уровней. Данное условие решается либо в процессе сбора и обработки данных, либо путем их пересчета.
Проблема сопоставимости данных особенно остро стоит в рядах динамики, потому что они охватывают значительные периоды времени, за которые могли произойти изменения и привести к несопоставимости статистических данных.
Основные причины несопоставимости уровней ряда динамики:
Различие в единицах измерения или единицах счета (например, нельзя сравнивать и анализировать цифры о производстве тканей, если за одни годы цифры даны в погонных метрах, а за другие – в квадратных метрах).
Различие в методологии учета или расчета показателей (например, если в одни годы среднюю урожайность считали с засеянной площади, а в другие – с убранной, то такие уровни будут несопоставимы).
Изменение круга охватываемых объектов вследствие перехода ряда объектов из одного подчинения в другое.
Изменение территориальных границ областей, районов, округов.
Следовательно, прежде чем анализировать динамический ряд, надо, исходя из цели исследования, убедиться в сопоставимости уровней ряда и при отсутствии последней добиваться ее, пользуясь дополнительными расчетами.
Привести уровни ряда к сопоставимому виду можно при помощи метода смыкания рядов динамики.
Под смыканием понимают объединение в один ряд (более длинный) двух или нескольких рядов динамики, уровни которых исчислены по разной методологии или разным территориальным границам.
Для осуществления смыкания необходимо, чтобы для одного из периодов (переходного) имелись данные, исчисленные по разной методологии (или в разных границах).
9.2. Аналитические показатели рядов динамики
Для количественной оценки развития явлений во времени используются аналитические показатели динамики. Они характеризуют в абсолютном или относительном выражении изменение значения показателя в одном уровне рассматриваемого ряда динамики по сравнению с другим уровнем.
К аналитическим показателям относятся:
абсолютный прирост;
темп роста и прироста;
абсолютное значение 1% прироста.
Возможны два способа сравнения уровней ряда динамики:
Расчет базисных показателей, при котором все уровни ряда сравниваются с фиксированным уровнем – базисным. Обычно за базисный берется начальный (первый) уровень.
Расчет цепных показателей, при котором каждый последующий уровень ряда динамики сравнивается с предыдущим.
Абсолютный прирост (∆) характеризует размер увеличения (или уменьшения) уровня ряда за определенный промежуток времени. Он равен разности двух сравниваемых уровней и выражает абсолютную скорость роста.
Базисный абсолютный прирост (
) рассчитывается по формуле
, (9.1)где
– i-й уровень ряда (текущий уровень);
– уровень ряда, принятый за базу сравнения.Цепной абсолютный прирост (
) рассчитывается по формуле
, (9.2)где
– уровень ряда, предшествующий i-му уровню ряда динамики.2. Показатель интенсивности изменения уровня ряда – в зависимости от того, выражается ли он в виде коэффициента или в процентах, принято называть коэффициентом роста или темпом роста. Иными словами, коэффициент роста и темп роста представляют собой две формы выражения интенсивности изменения уровня. Разница между ними заключается только в единице измерения.
Коэффициент роста (
) показывает, во сколько раз данный уровень ряда больше предыдущего или базисного уровня (если этот коэффициент больше единицы) или какую часть от предыдущего или базисного уровня (если этот коэффициент меньше единицы) он составляет.Темп роста (
) показывает, сколько процентов составляет величина показателя в текущем периоде по сравнению с его величиной в предшествующем (или базисном) периоде.Темп роста базисный (
) рассчитывается по формуле
. (9.3)Темп роста цепной (
) рассчитывается по формуле
. (9.4)Темп роста всегда положителен. Если темп роста равен 100%, то значение уровня не изменилось по сравнению со сравниваемым уровнем; если больше 100%, то значение уровня повысилось, а если меньше 100% – значение понизилось.
3. Темп прироста (
) показывает, на сколько процентов изменился сравниваемый уровень по отношению к уровню, принятому за базу сравнения.Темп прироста базисный (
) рассчитывается по формуле
,или
, (9.5)где
– темп роста базисный, соответствующий i-му моменту; – абсолютный прирост базисный, соответствующий i-му моменту.Темп прироста цепной (
) рассчитывается по формуле
, или 
, (9.6)где
– темп роста цепной, соответствующий i-му моменту;
– абсолютный прирост цепной, соответствующий i-му моменту.Значение темпа прироста может быть равно нулю, может быть больше нуля и меньше нуля.
4. Абсолютное значение 1% прироста (А) представляет собой отношение значения абсолютного прироста показателя к его темпу прироста в i-й момент времени:
, или 
. (9.7)Расчет данного показателя базисным методом не имеет смысла, потому что для каждого периода эта будет одна и та же величина – сотая часть уровня базисного периода.
9.3. Средние показатели рядов динамики
Особое внимание при анализе рядов динамики следует уделять методам расчета средних показателей рядов динамики, которые являются обобщающими характеристиками его абсолютных уровней, абсолютной скорости и интенсивности изменения уровней ряда динамики. Для обобщений данных рассчитываются:
средний уровень ряда динамики;
средний абсолютный прирост;
средний темп роста и прироста.
Средний уровень ряда динамики. Определение среднего уровня ряда динамики зависит от его вида и способов получения статистических данных.
В интервальном ряду динамики с равноотстоящими уровнями во времени расчет среднего уровня ряда производится по формуле средней арифметической простой
, (9.8)где
– число уровней ряда, участвующих в расчете.В интервальном ряду динамики с неравноотстоящими уровнямисредний уровень ряда вычисляется по формуле средней арифметической взвешенной
, (9.9)где
– продолжительность интервалов времени между уровнями (число периодов времени, в течение которых значение уровня не изменялось).Средний уровень моментного ряда динамики рассчитывается по формуле средней хронологической. Для моментного ряда с равноотстоящими уровнями при расчете среднего уровня используют формулу средней хронологической простой:
, (9.10)где
, …, 
– уровни ряда;
– число уровней ряда, участвующих в расчете.Средний уровень моментного ряда с неравноотстоящими уровнями определяется по формуле средней хронологической взвешенной:
, (9.11)где
– продолжительность интервалов времени между соседними уровнями.Средний абсолютный прирост является обобщающим показателем абсолютной скорости изменения во времени за весь период, ограничивающий ряд динамики. Скоростью в данном случае будем назвать прирост (уменьшение) в единицу времени. Для его определения используется формула средней арифметической простой
, или 
, (9.12)где
– цепные абсолютные приросты; и – соответственно конечный и начальный уровни ряда динамики.Средний темп роста и прироста является сводной обобщающей характеристикой интенсивности изменения уровней ряда динамики. Он показывает, сколько в среднем процентов последующий уровень составляет от предыдущего в течение всего периода наблюдения:
, или 
, (9.13)где
– коэффициенты роста; это темпы роста цепные, только выраженные не в процентах, а в коэффициентах;m – число коэффициентов роста.
Средний темп прироста не может быть определен непосредственно на основании цепных темпов прироста или показателей среднего абсолютного прироста. Для его вычисления необходимо вначале найти средний темп роста, а затем уменьшить его на 100%:
. (9.14)
Пример 15. Имеются данные о производстве макаронных изделий в РФ за период с 2003–2009 гг. (информация взята с сайта gks.ru):| Год | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 |
| Производство макаронных изделий, тыс.т. | 874 | 958 | 993 | 1036 | 1014 | 1027 | 1048 |
Определите показатели, характеризующие тенденцию развития данного явления, а также средние показатели ряда динамики.
1. Рассчитаем аналитические показатели ряда динамики базисным и цепным методом и представим результат в таблице.
Для расчета показателей базисным методом возьмем за базу сравнения начальный уровень 2003 г.
| Годы | Производство макаронных изделий, тыс.т | Абсолютный прирост, тыс. т | Темп роста, % | Темп прироста, % | Абсолютное значение 1% прироста, тыс. т | |||
| базисный | цепной | базисный | цепной | базисный | цепной | |||
| 2003 | 874 | – | – | 100,0 | – | – | – | – |
| 2004 | 958 | 84 | 84 | 109,6 | 109,6 | 9,6 | 9,6 | 8,74 |
| 2005 | 993 | 119 | 35 | 113,6 | 103,7 | 13,6 | 3,7 | 9,58 |
| 2006 | 1036 | 162 | 43 | 118,5 | 104,3 | 18,5 | 4,3 | 9,93 |
| 2007 | 1014 | 140 | –22 | 116,0 | 97,9 | 16,0 | –2,1 | 10,36 |
| 2008 | 1027 | 153 | 13 | 117,5 | 101,3 | 17,5 | 1,3 | 10,14 |
| 2009 | 1048 | 174 | 21 | 119,9 | 102,0 | 19,9 | 2,0 | 10,27 |
| Итого | 6950 | | 174 | | | | | |
Для выражения абсолютной скорости роста (снижения) уровня ряда динамики исчисляют статистический показатель – абсолютный прирост. Его величина вычисляется для базисного и цепного метода соответственно по формулам (9.1) и (9.2).
Абсолютный прирост базисный показывает, сколько составил прирост (уменьшение) производства макаронных изделий в каждом году по сравнению с уровнем базисного 2003 г.
Абсолютный прирост цепной показывает, на сколько (тыс. т) увеличилось (или уменьшилось) производство макаронных изделий в каждом последующем году по сравнению с предыдущим.
Интенсивность изменения уровней ряда динамики оценивается отношением текущего уровня к предыдущему или базисному, которое всегда представляет собой положительное число. Этот показатель называют темпом роста. Он выражается в процентах и рассчитывается для базисного и цепного метода соответственно по формулам (9.3) и (9.4).
Базисные темпы роста характеризуют непрерывность развития явления. В данном случае производство макаронных изделий сравнивается с первоначальным уровнем (с уровнем 2003 г.), равным 874 тыс. т и принятым за 100%. Показатели базисных темпов роста свидетельствуют о постоянном увеличении производства макаронных изделий.
Цепные темпы роста показывают интенсивность роста производства макаронных изделий для каждого года. В динамике производства имел место спад в 2007 г.
Темп роста может быть выражен и в виде коэффициента, в этом случае он показывает, во сколько раз данный уровень ряда больше уровня базисного года или какую его часть он составляет.
Для выражения изменения величины абсолютного прироста уровней ряда динамики (в относительных величинах) определяется темп прироста, который рассчитывается для базисного и цепного методов соответственно по формулам (9.5) и (9.6).
Темпы прироста показывают прирост (или снижение) производства макаронных изделий в относительных величинах, т.е. по сравнению со 100%. Если уровни ряда динамики сокращаются, то показатели темпа прироста будут со знаком «–». В данном примере, при базисном методе расчета, происходит прирост производства макаронных изделий по сравнению с 2003 г. При цепном методе расчета производство макаронных изделий сократилось в 2007 г.
Показатель абсолютного значения одного процента прироста рассчитывается по формуле (9.7) и имеет экономический смысл только для цепной основы.
2.Рассчитаем средние показатели. Определим вид уровня ряда динамики – у нас представлен интервальный ряд с равноотстоящими уровнями, поэтому для расчета среднего уровня ряда динамики воспользуемся формулой (9.8):
тыс. т.Вывод. В среднем в период с 2003 по 2009 гг. в РФ ежегодно производилось 992,86 тыс. т макаронных изделий.
Средний абсолютный прирост рассчитаем двумя способами по формулам (9.12):
тыс. т,или
тыс. т.Вывод. В среднем ежегодно производство макаронных изделий в РФ увеличивалось на 29 тыс. т.
Средний темп роста рассчитаем двумя способами по формуле (9.13):
или
.Вывод. Среднегодовой темп роста составил 102,5%, в среднем ежегодно производство макаронных изделий увеличивалось в 1,023 раза.
Средний темп прироста рассчитаем по формуле (9.14):
.Вывод. В среднем ежегодный прирост производства макаронных изделий составил 2,5 %.
9.4. Аналитическое выравнивание рядов динамики
Важной задачей статистики при анализе рядов динамики является определение основной тенденции развития, присущей тому или иному ряду динамики.
Под основной тенденцией развития ряда динамики понимают изменение, определяющее общее направление развития. Это – систематическая составляющая долговременного действия.
Например, за колебаниями урожайности какой-либо зерновой культуры в отдельные годы тенденция роста (уменьшения) может не просматриваться непосредственно, и поэтому должна быть выявлена статистическими методами.
Наиболее эффективным статистическим методом выявления основной тенденции развития является аналитическое выравнивание с применением кривой, проведенной между конкретными уровнями таким образом, чтобы она отражала тенденцию, присущую ряду, и одновременно освободила его от незначительных колебаний.
Аналитическое выравнивание позволяет достаточно точно установить характер развития явления и описать его математически, а также, что является наиболее важным, использовать полученную модель для прогнозирования. Аналитическое выравнивание предполагает представление уровней ряда динамики в виде функции времени
.Данная математическая функция, описывающая закономерность развития явления во времени, называется уравнением тренда.
Правильно построенная модель должна соответствовать характеру изменения тенденции исследуемого явления. Выбранная функция позволяет получить выравненные (или теоретические) значения уровней ряда динамики.
Первым шагом в проведении аналитического выравнивания является выбор вида математической функции, которую предполагают принять в качестве модели тренда. При этом можно руководствоваться формой кривой, полученной на основе отображения на графике эмпирических данных. Схема построения графика достаточно проста: по оси абсцисс откладываются временные периоды (даты), по оси ординат – значения уровней ряда динамики. По характеру скопления нанесенных точек судят о предполагаемом виде модели (функции).
В динамическом анализе в качестве линии тренда чаще всего используются следующие функции:
линейная:
;парабола 2-го порядка:
;гиперболическая:
.Оценка параметров в функциях находится методом наименьших квадратов, суть которого состоит в определении таких параметров (коэффициентов), при которых сумма квадратов отклонений расчетных значений уровней от фактических значений была минимальной. Таким образом, эти оценки находятся в результате минимизации выражения
, (9.15)где
– фактическое значение уровня ряда динамики;
– расчетное значение;t – длина ряда динамики.
Система нормальных уравнений для оценки параметров имеет следующий вид:
для прямой
(9.16)для параболы 2-го порядка
(9.17)для гиперболы
(9.18)При нахождении параметров уравнения для упрощения расчетов показателям времени t придают такие значения, чтобы их сумма была равна нулю, т.е.
. (9.19)Для этого при нечетном количестве уровней ряда серединному уровню присваивают значение t = 0, предыдущим – значения –1, –2, –3 и т.д. (с шагом –1 от середины ряда), последующим - 1, 2, 3 и т.д. (с шагом 1 от середины ряда).
При четном количестве уровней ряда в середине графы условного показателя времени t присваивают значения –1 и +1, для остальных периодов значения идут с шагом, равным двум единицам.
Таким образом, получаем следующее распределение условного показателя t:
для нечетного числа уровней ряда
= …; –3; –2; –1; 0; 1; 2; 3; …для четного числа уровней ряда ti= …; –5; –3; –1; 1; 3; 5; …
В любом случае
. Применяя данное условие, можно упростить систему нормальных уравнений для расчета показателей:для прямой
формула (9.16) примет вид
(9.20)для параболы 2-го порядка
формула (9.17) примет вид
(9.21)Замечание. При нахождении параметров уравнения гиперболы обозначение условного показателя времени t производится на основе простой нумерации периодов: 1, 2, 3, 4 и т.д., начиная с первого уровня. Пользоваться принципом обозначения условного показателя t, который применим для других уравнений, невозможно из-за выражения
, при котором 
. Пример 16. Определить основную тенденцию строительства квартир в РФ за 2006–2011 гг., которая представлена в табл. 29 (информация взята с сайта gks.ru):Таблица 29
Число построенных квартир в РФ за период 2006–2011 гг.
| Год | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 |
| Число построенных квартир, тыс. | 609 | 722 | 768 | 702 | 717 | 786 |
Решение. Проведем аналитическое выравнивание ряда динамики по прямой, используя уравнение
.Найдем параметры
и 
методом наименьших квадратов, решая систему из двух уравнений (9.16). Принимаем, что . В данном примере число уровней ряда четное (6), т.е. = –5; –3; –1; 1; 3; 5.Тогда система уравнений примет вид (9.20):
Из данной системы параметры
и 
находятся следующим образом:
и
.Произведем дополнительные вычисления (табл. 30) для нахождения параметров
и .Воспользуемся дополнительными вычислениями (табл. 30) и определим параметры
и :
и 
.Таблица 30
Число построенных квартир в РФ за период 2006–2011 гг.
(дополнительные вычисления)
| Годы | Число построенных квартир, тыс. |  |  |  |  |
| 2006 | 609 | –5 | 25 | –3045 | 659,88 |
| 2007 | 722 | –3 | 9 | –2166 | 682,86 |
| 2008 | 768 | –1 | 1 | –768 | 705,84 |
| 2009 | 702 | 1 | 1 | 702 | 728,82 |
| 2010 | 717 | 3 | 9 | 2151 | 751,80 |
| 2011 | 786 | 5 | 25 | 3930 | 774,78 |
| Итого | 4304 | 0 | 70 | 804 | 4304 |
По рассчитанным параметрам получаем уравнение основной тенденции строительства квартир в РФ, т.е. модель тренда
.Используя приведенное уравнение, рассчитаем для каждого года выравненные уровни ряда динамики (
) путем подстановки в него значений t:
;
и т.д. (см. табл. 30).
Правильность расчета уровней выравниваемого ряда динамики может быть проверена следующим образом: сумма значений эмпирического ряда должна совпадать с суммой вычисленных уровней выравненного ряда, т.е.
. В нашем случае суммы совпадают, что свидетельствует о правильности вычислений.Представим результаты произведенного аналитического выравнивания ряда динамики числа построенных квартир в РФ за 2006–2011 гг. и эмпирических (фактических) данных на рис. 27.
Рис. 27. Динамика строительства квартир в РФ
за период с 2006–2011 гг.
Используя полученное уравнение тренда, можно провести экстраполяцию ряда динамики (установить значения, соответствующие основной тенденции развития явления в последующие периоды или моменты времени). Экстраполяция – продление в будущем тенденции, наблюдавшейся в прошлом.
Так, например, определим прогнозные значения количества построенных квартир в РФ в 2012 г. Для этого подставим в полученное уравнение тренда значение t=7, тогда
тыс.Вывод. Прогнозное значение количества построенных квартир в2012 г. составит 797,76 тыс.
Вопросы и задания для самоконтроля
Дайте определение ряда динамики социально-экономических явлений. Как строится ряд динамики?
Какие виды рядов динамики вы знаете?
Как произвести расчет среднего уровня в моментных и интервальных рядах динамики?
Что характеризуют показатели абсолютного прироста, темпа роста и темпа прироста? В чем разница между этими показателями?
Как провести аналитическое выравнивание ряда динамики по уравнению прямой?