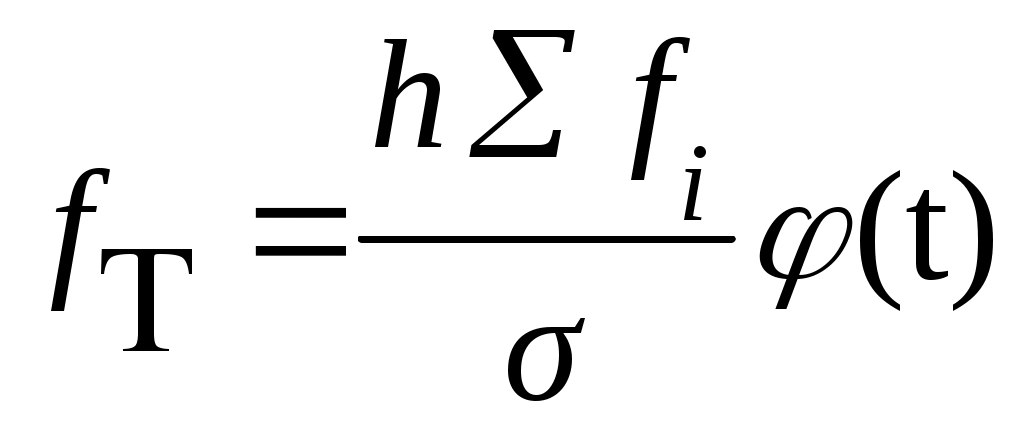УП_Теория статистики_080200 испр.(. Томский политехнический университет н. В. Шаповалова, Н. В. Королева, Т. В. Громова теория статистикИ
 Скачать 3.39 Mb.
|
6.4. Показатели асимметрии и эксцессаДля обобщающей характеристики особенностей формы распределения применяются кривые распределения. Кривая распределения выражает графически (полигон, гистограмма) закономерность распределения единиц совокупности по величине варьирующего признака. Различают эмпирические и теоретические кривые распределения.  Эмпирическая кривая распределения – это фактическая кривая распределения, полученная по данным наблюдения, в которой отражаются как общие, так и случайные условия, определяющие распределение. Теоретическая кривая распределения – это кривая, выражающая функциональную связь между изменением варьирующего признака и изменением частот и характеризующая определенный тип распределения. При этом теоретическое распределение играет роль некоторой идеализированной модели эмпирического распределения, а сам анализ вариационного ряда сводится к сопоставлению эмпирического и теоретического распределений.Кривые распределения бывают симметричными и асимметричными. В зависимости от того, какая ветвь кривой вытянута – правая или левая, различают правостороннюю или левостороннюю асимметрию. Кривые распределения могут быть одно-, двух и многовершинными. Для однородных совокупностей, как правило, характерны одновершинные распределения. Многовершинность свидетельствует о неоднородности изучаемой совокупности. Появление двух и более вершин делает необходимой перегруппировку данных с целью выделения более однородных групп. Для симметричных распределений частоты двух вариант, равноотстоящих в обе стороны от центра, равны между собой. Рассчитанные для таких рядов распределений характеристики равны:  .Если указанные соотношения нарушены, то это свидетельствует о наличии асимметрии распределения. Так, при  , разности между  и  положительные и асимметрия правосторонняя, а при  , наоборот, разности и отрицательные и асимметрия левосторонняя.При сравнительном изучении асимметрии нескольких распределений с разными единицами измерения вычисляется относительный показатель асимметрии или коэффициент асимметрии Пирсона (As):  или  (6.26)В одновершинных распределениях величина данного показателя изменяется от – 1 до + 1. В симметричных распределениях As=0. Его величина может быть положительной и отрицательной. Если величина положительная – то асимметрия правосторонняя (рис. 17 а), если – отрицательная, то асимметрия левосторонняя (рис. 17 б). 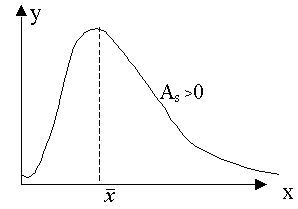 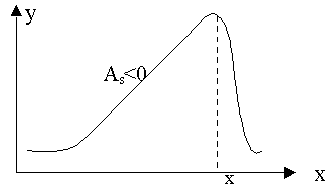 a б Рис. 17. a) правосторонняя асимметрия; б) левосторонняя асимметрия Чем ближе  к 1, тем асимметрия существеннее:если  < 0,25, то асимметрия считается незначительной;если 0,5 < < 0,25, то асимметрия считается умеренной;если > 0,5, то асимметрия значительная.Коэффициент асимметрии Пирсона характеризует асимметрию только центральной части распределения, поэтому более распространенным и более точным является коэффициент асимметрии, рассчитанный на основе центрального момента 3-его порядка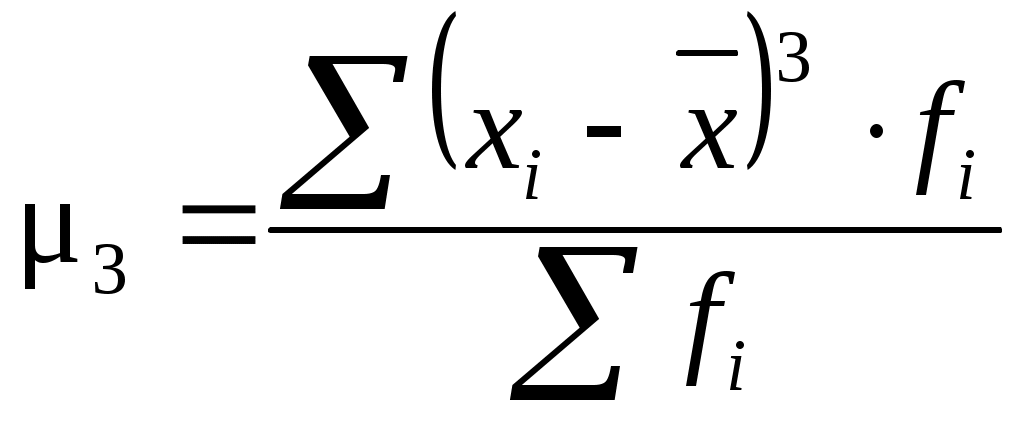.  (6.27)где  – центральный момент третьего порядка; – среднее квадратическое отклонение в третьей степени. (6.28) Центральным моментом называется среднее отклонение индивидуальных значений признака от его среднеарифметической величины.Если As> 0, то асимметрия правосторонняя, а если As< 0, то асимметрия левосторонняя. Чем числитель ближе к 0, тем асимметрия меньше. Оценка существенности As проводится на основе средней квадратической ошибки коэффициента асимметрии  , которая зависит от числа наблюдений ( ) и рассчитывается по формуле: (6.29)В случае  >3, асимметрия является существенной и распределение признака в генеральной совокупности несимметрично. В противном случае асимметрия несущественна и ее наличие может быть вызвано случайными обстоятельствами.Для одновершинных распределений рассчитывается еще один показатель оценки его формы – эксцесс. Эксцесс рассчитывается для симметричных распределений на основе центрального момента 4-ого порядка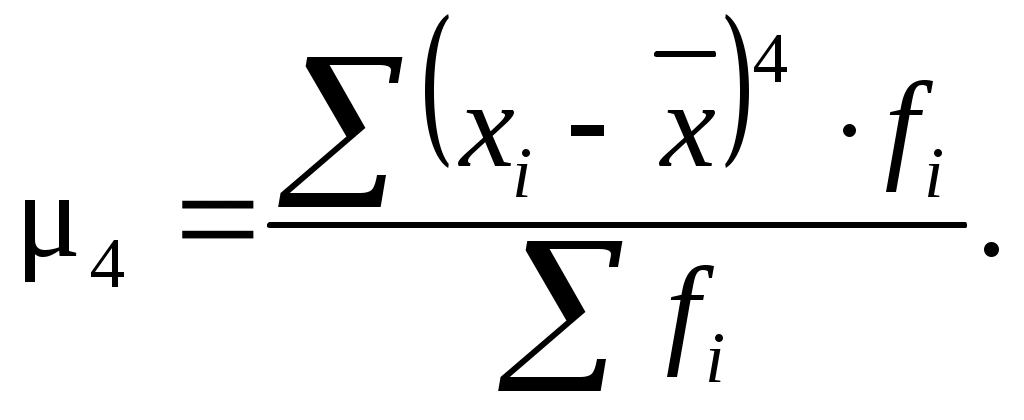.  (6.30)где  – центральный момент четвертого порядка; – среднее квадратическое отклонение в четвертой степени. (6.31)При симметричном (нормальном) распределении Ek= 0. Если Ek> 0, то распределение считается островершинным (рис. 18 a), если Ek< 0, то распределение считается плосковершинным (рис. 18 б).   a b Рис. 18. a) островершинное распределение; б) плосковершинное распределение Среднеквадратическая ошибка эксцесса  рассчитывается по формуле: (6.32)где – число наблюдений. Пример 7. Имеется распределение коммерческих банков РФ по размеру выданных кредитов, представленные в таблице 12 (данные условные). Определите коэффициент асимметрии и эксцесса.Таблица 12 Распределение коммерческих банков РФ по размеру выданных кредитов, млн. р.
Дополнительные расчеты произведем в табл. 12. Рассчитаем  по формуле (5.10) млн. р.Рассчитаем коэффициент асимметрии по центральному моменту 3-его порядка по формуле (6.27). Для этого определим центральный момент 3-его порядка (формула 6.28) и среднее квадратическое отклонение (формула 6.7): 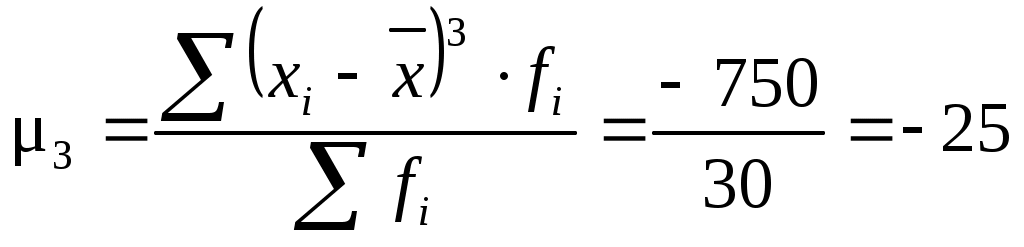 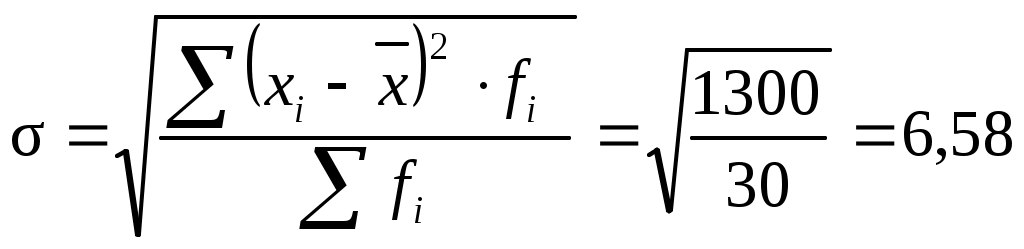  Рассчитаем показатель эксцесса по формуле (6.30). Для этого рассчитаем центральный момент 4-ого порядка (6.31): 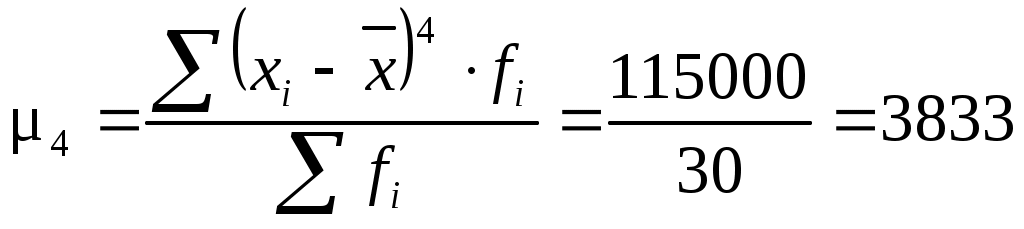  Полученный результат свидетельствует о том, что распределение является плосковершинным. Вывод. Значение коэффициента асимметрии свидетельствует о незначительной левосторонней асимметрии. Полученный результат показателя эксцесса свидетельствует о том, что распределение является плосковершинным. 6.5. Теоретические кривые распределенияАнализ вариационных рядов предполагает выявление закономерностей распределения, определение и построение (получение) некой теоретической (вероятностной) формы распределения. Характер распределения лучше всего проявляется при большом числе наблюдений и малых интервалах. В этом случае графическое изображение эмпирического вариационного ряда принимает вид плавной кривой, именуемой кривой распределения. Кривая распределения может рассматриваться как некая теоретическая (вероятностная) форма распределения, свойственная определенной совокупности в конкретных условиях. Анализируя частоты в эмпирическом распределении, можно описать это распределение с помощью математической модели — закона распределения, установить по исходным данным параметры теоретической кривой и проверить правильность выдвинутой гипотезы о типе распределения данного ряда. В практике статистического исследования встречаются различные распределения: нормальное, логарифмически нормальное, биномиальное, Пуассона, Шарлье и др. Каждое распределение имеет свою специфику и область применения. Нормальное распределение При построении статистических моделей наиболее широко применяется нормальное распределение (закон Гаусса – Лапласса). В 1727 г. английский математик Абрахам де Муавр (1667-1754) открыл закон распределения, вероятностей, названный законом нормального распределения. Вначале XIX в. данными вопросами занимались Пьер Лаплас (1749-1827) и Карл Гаусс (1777-1855). Общие условия возникновения закона нормального распределения установил А.М Ляпунов (1857-1918). Распределения, близкие к нормальному распределению, были обнаружены при изучении самых различных явлений, как в природе, так и в развитии общества. Нормальное распределение признака наблюдается в тех случаях, когда на величину вариантов, входящих в состав вариационного ряда, действует множество случайных, независимых или слабо зависимых факторов, каждый из которых играет в общей сумме незначительную роль. Нарушение нормального характера распределения часто является свидетельством неоднородности совокупности. Закон нормального распределения выражается формулой: (6.33)где  – ордината кривой нормального распределения; – стандартизованная (нормированная) величина;e– основание натурального логарифма (e=2,7183); π– постоянное число (π= 3,1416); xi – варианты вариационного ряда;  – средняя величина; – среднее квадратическое отклонение. Функция широко используется в экономических расчетах, а ее значение при разных tтабулированы и представлены в математических таблицах. При графическом изображении плотности распределении получим кривую нормального распределения, симметричную относительно вертикальной прямой х =  (рис. 19), поэтому величину называют центром распределения.Случайные величины, распределенные по нормальному закону, различаются значениями параметров 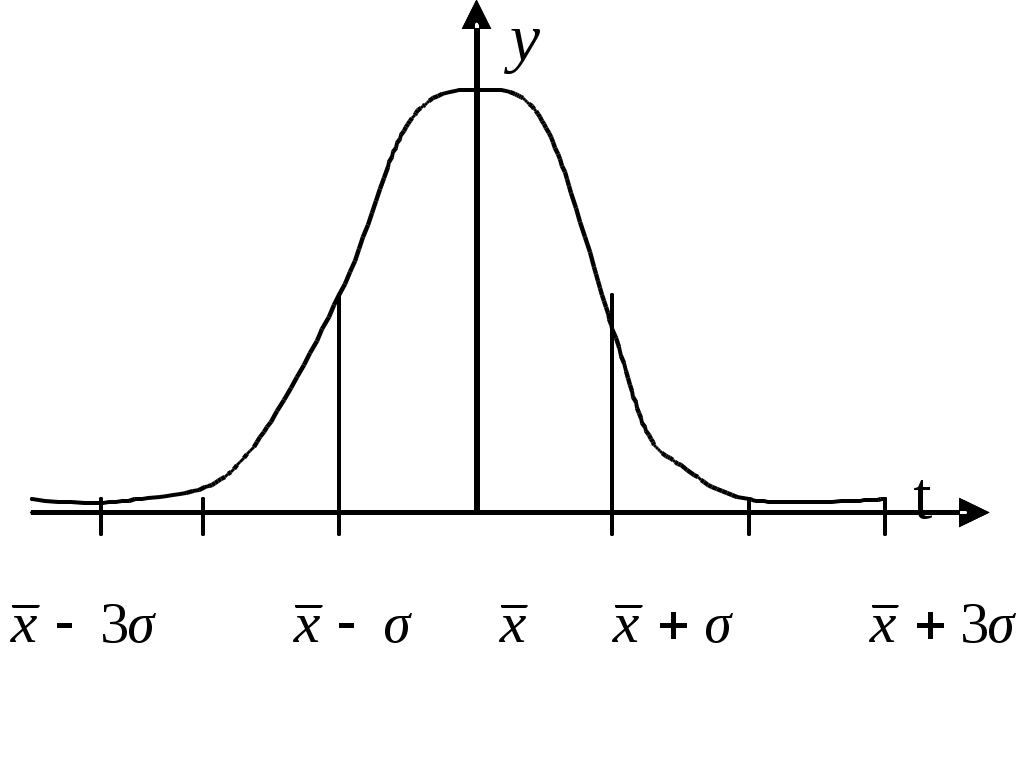и , поэтому очень важно выяснить, как эти параметры влияют на вид нормальной кривой. Рис. 19. Нормальное распределение с одно-, двух-, трехсигмовыми пределами Свойства кривой нормального распределения: 1. Функция нормального распределения четная, т.е. y(-t)=y(+t). Следовательно, изображающая ее кривая распределена симметрично относительно оси ординат, т.е. .2. Функция имеет бесконечно малые значения при t= . Это означает, что ветви кривой удалены в бесконечность и асимптотически приближаются к оси абсцисс. 3. Кривая имеет две точки перегиба на расстоянии от .4. Коэффициенты асимметрии и эксцесса равны нулю. 5. Площадь между ординатами, проведенными на расстоянии . составляет 0,683. Это означает, что при t= 1 заключается 68,26% всех значений признаков; между 2 при t= 2 располагается 95,44% всех значений признаков; между 3 при t= 3 находится 99,73% значений признаков. На рис. 19 показано нормальное распределение с одно-, двух-, трехсигмовыми пределами.На практике почти не встречаются отклонения, которые превышают 3. Отклонение 3 может считаться максимально возможным. Это положение называют “правилом трех сигм” В математической статистике нормальное распределение играет роль некоторого стандарта, с которым сравнивают другие распределения. Порядок расчета теоретических частот кривой нормального распределения следующий: по эмпирическим данным рассчитывают среднюю арифметическую ряда и среднее квадратическое отклонение ;для каждой варианты вычисляют величину  , называемой нормированными отклонениями от средней;по таблице распределения функции y(t)=  определяют ее значения (см. Приложение 1);вычисляют теоретические частоты по формуле: 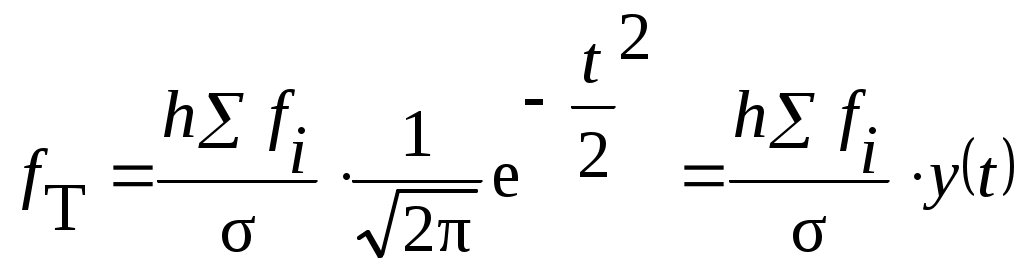  (6.34)где h– величина интервала; fi– сумма всех частот, равная объему совокупности; – среднее квадратическое отклонение. Если вариационный ряд имеет равные интервалы, тогда  (6.35)6.6. Критерии согласияТак как все предположения о характере того или иного распределения – это гипотезы, а не категорические утверждения, то они должны быть подвергнуты статистической проверке с помощью так называемых критериев согласия. Критерии согласия, опираясь на установленный закон распределения, дают возможность установить, когда расхождения между теоретическими и эмпирическими частотами следует признать несущественными (случайными), а когда – существенными (неслучайными). Таким образом, критерии согласия позволяют отвергнуть или подтвердить правильность выдвинутой при выравнивании ряда гипотезы о характере распределения в эмпирическом ряду и дать ответ, можно ли принять для данного эмпирического распределения модель, выраженную некоторым теоретическим законом распределения. Существует ряд критериев согласия, среди которых наиболее чаще применяют критерии Пирсона, Романовского и Колмогорова. Рассмотрим их более подробно. Критерий согласия Пирсона ( ) вычисляется по формуле: (6.36)где  эмпирические и теоретические частоты соответственно.Фактическое значение  сравнивают с критическим, которое находится по специальным таблицам в зависимости от принимаемого уровня значимости и числа степеней свободы (см. Приложение 2).Уровень значимости (α) – вероятность ошибочного отклонения выдвинутой гипотезы, т.е. вероятность того, что будет отвергнута правильная гипотеза. В зависимости от важности и ответственности решаемых задач в статистических исследованиях используют следующие три уровня значимости: α = 0,10, P(t) = 0,90; α = 0,05, P(t) = 0,95; α = 0,01, P(t) = 0,99. Например, вероятность 0,01 означает, что в одном случае из 100 может быть отвергнута правильная гипотеза. В экономических исследованиях приемлемой считается вероятность ошибки 0,05, т.е. в 5 случаях из 100 может быть отвергнута правильная гипотеза. Число степеней свободы (ν) рассчитывается как число групп в ряду распределения минус единица и минус число параметров эмпирического распределения, использованных для нахождения теоретических частот. Так, при выравнивании по кривой нормального распределения число степеней свободы ν=n-1-2, поскольку при расчете теоретических частот используется два параметра эмпирического распределения:и т.е. ν=n-3.Для оценки существенности расчетное значение  сравнивается с табличным  . При полном совпадении теоретического и эмпирического распределений =0, в противном случае >0. Если  > , то при заданном уровне значимости (α) и числе степеней свободы (ν) гипотезу о несущественности (случайности) расхождений отклоняем. Если фактическое (расчетное) оказывается меньше табличного (критического), т.е. < то расхождения между эмпирическими и теоретическими частотами можно считать случайными. Критерий Романовского (C), также используемый для проверки близости эмпирического и теоретического распределений, определяется следующим образом: , (6.37)где – расчетная величина критерия Пирсона;ν– число степеней свободы, ν= n– 3, n– число интервальных групп. При С<3 различие несущественно, что позволяет считать эмпирическое распределение близким к нормальному. 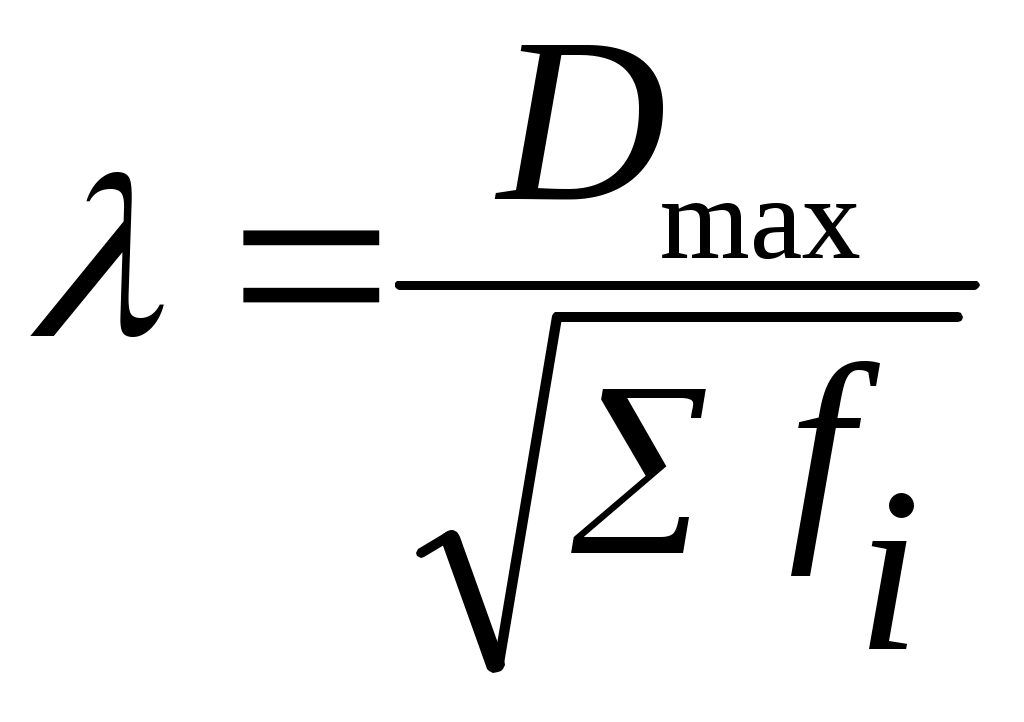Критерий Колмогорова () вычисляется по формуле: , (6.38)где Dmax– максимальное значение разности между накопленными эмпирическими и теоретическими частотами;  – сумма эмпирических частот (объем совокупности).Рассчитав значение λ, по таблице (см. Приложение 3) определяют вероятность Р(λ), с которой можно утверждать, что отклонения эмпирических частот от теоретических случайны. Вероятность Р(λ) может изменяться от 0 до 1. При Р(λ)=1 происходит полное совпадение частот, при Р(λ)=0 – полное расхождение. Если λ принимает значения до 0,3, то Р(λ)=1. Необходимым условием использования этого критерия является достаточно большое число наблюдений (не меньше 100). Пример 8: Имеются данные по цеху о распределении рабочих по стажу работы (табл. 13). На основе приведенных данных проверить соответствие эмпирического распределения закону нормального распределения, используя критерий согласия Пирсона.Таблица 13
Выдвинув гипотезу о нормальном распределении, определим по эмпирическим данным параметры этой кривой. Сначала рассчитаем средний уровень ряда по формуле (5.10), используя данные графы 4 табл. 13:  Затем определим среднее квадратическое отклонение по формуле 6.7, используя промежуточные расчеты графы 5 табл. 13: 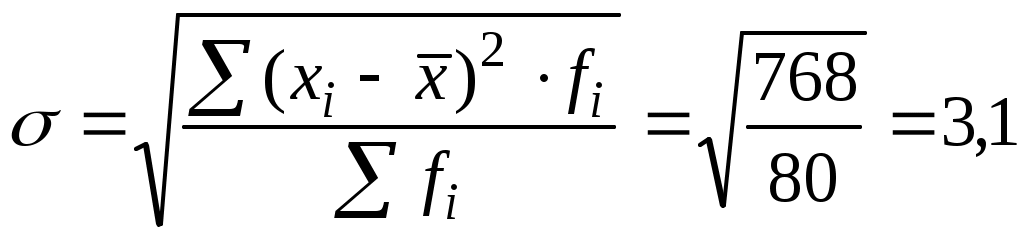 года.Далее определим нормированное отклонение tдля каждого варианта (см. графу 6 табл. 13), после чего по таблице распределения функции (см. Приложение 1) найдем значения функции при значениях аргумента, полученных в графе 6. При этом необходимо учитывать, что функция четная, т.е.  = .Анализируемый вариационный ряд имеет равные интервалы, следовательно, можно определить:  .Последовательно умножив const на величину для каждого варианта, получим теоретические частоты  (см. графу 8 табл.13). Иногда за счет округлений при расчетах может быть нарушено равенство сумм эмпирических и теоретических частот, что и произошло в данном случае (  )Сравним на графике эмпирические и теоретические частоты, полученные на основе данных табл. 13 (рис. 20). 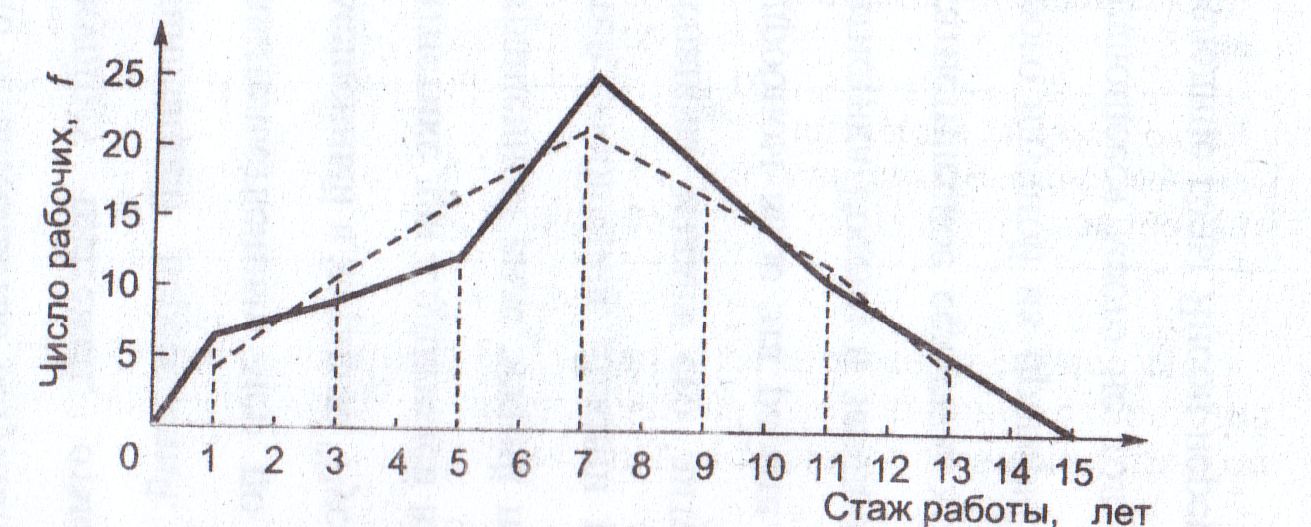 ─ эмпирическое распределение; ---- теоретическая кривая нормального распределения Рис. 20. Распределение рабочих по стажу работы Сопоставление на графике эмпирического распределения с теоретической кривой нормального распределения свидетельствует о достаточно хорошем согласовании распределений. Степень расхождения теоретических и эмпирических частот оценивается с помощью критерия К. Пирсона (см. графу 9 табл.13): 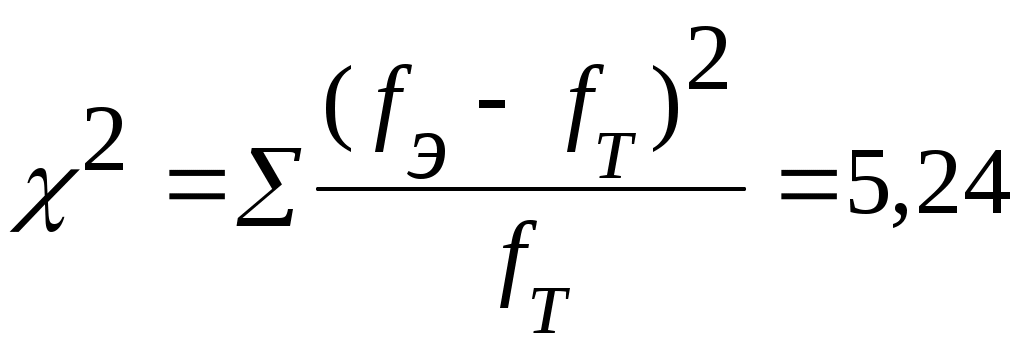 .Полученное значение критерия  сравнивается с табличным значение  , которое определяется по таблице (см. Приложение 2).При вероятности Р(t)=0,95 (α = 0,05) и числе степеней свободы ν=n-3=7 – 3=4 (n – число групп, в нашем примере 7 групп) получим табличное значение  =9,5.На основе проведенных расчетов получаем, что  < (5,24<9,5), следовательно, гипотеза о близости эмпирического распределения к нормальному не отвергается, а расхождения объясняются случайными факторами.
|
