|
|
УП_Теория статистики_080200 испр.(. Томский политехнический университет н. В. Шаповалова, Н. В. Королева, Т. В. Громова теория статистикИ
Проверь себя
Выберите правильный вариант ответа.
Обобщающие абсолютные величины характеризуют:
а) отдельные единицы совокупности;
б) определенные чисти совокупности;
в) всю совокупность в целом.
Отношения частей изучаемой совокупности к одной из них, принятой за базу сравнения, называются относительными величинами:
а) планового задания;
б) выполнения плана;
в) динамики;
г) структуры;
д) координации;
е) сравнения;
ж) интенсивности.
К какому виду относительных величин относится показатель уровня ВВП РФ на душу населения:
а) динамики;
б) планового задания;
в) выполнения плана;
г) структуры;
д) координации;
е) интенсивности и уровня экономического развития;
ж) сравнения.
Средняя величина может быть исчислена:
а) для количественного признака;
б) атрибутивного признака;
в) альтернативного признака.
Возраст одинаковых по численности групп лиц составил (лет): 20, 30 и 40. Средний возраст всех лиц будет:
а) менее 30 лет;
б) равен 30 годам;
в) более 30 лет.
В каких случаях взвешенные и невзвешенные средние равны между собой:
а) при отсутствии весов;
б) при равенстве весов;
в) при отсутствии или равенстве весов?
МОДУЛЬ 2
АНАЛИТИЧЕСКАЯ СТАТИСТИКА Глава 6
Показатели вариации 6.1. Абсолютные и относительные показатели вариации
 Вариация – это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени. Вариация – это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени.
Вариация возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае.
Исследование вариации в статистике имеет важное значение. Измерение вариации дает возможность оценить степень воздействия на данный признак других варьирующих признаков, установить, например, какие факторы и в какой степени влияют на смертность населения, доходы и расходы населения, финансовое положение предприятий, урожайность сельского хозяйства и т.д.
Задача изучения вариации признаков состоит в том, чтобы:
1) определить меру вариации, т.е. количественно измерить (рассчитать показатель вариации);
2) выяснить причины, которые вызвали вариацию признаков. Разложить общий объем вариации по источникам.
Средняя величина – обобщающая характеристика признака изучаемой совокупности, но она не показывает строение совокупности, не дает представление о том, как отдельные значения изучаемого признака группируются вокруг средней, сосредоточены ли они вблизи или значительно отклоняются от нее.
К абсолютным показателям вариации относятся:
размах вариации;
среднее линейное отклонение;
дисперсия;
среднее квадратическое отклонение.
Абсолютные показатели являются так называемыми характеристиками рассеяния. Они оценивают колеблемость значений признака или вариантов около их средней арифметической величины, т.е. отклонение вариантов от нее. Чем больше такие отклонения, тем значительнее вариация изучаемого признака.
Абсолютные показатели вариации имеют те же единицы измерения, что и исследуемый показатель вариационного ряда.
 Размах вариации – это разность между максимальным и минимальным значениями варьирующего признака: Размах вариации – это разность между максимальным и минимальным значениями варьирующего признака:
 . (6.1) . (6.1)
Основным недостатком этого показателя является то, что он определяется двумя крайними значениями, в то время как вариация признака складывается из всех его значений. Им определяются пределы, в которых могут колебаться размеры тех или иных параметров деталей, при контроле качества продукции и т.д.
 Среднее линейное отклонение представляет собой среднюю арифметическую из абсолютных значений всех отклонений индивидуальных значений признака от среднего: Среднее линейное отклонение представляет собой среднюю арифметическую из абсолютных значений всех отклонений индивидуальных значений признака от среднего:
простое:  (6.2) (6.2)
взвешенное:  (6.3) (6.3)
Основным недостатком среднего линейного отклонения является то, что в нем не учитываются знаки отклонений, т.е. их направленность. Поэтому этот показатель вариации используется редко. Показателями вариации, которые бы устранили недостатки среднего линейного отклонения, являются дисперсия и среднее квадратическое отклонение.
 Дисперсией называется средний квадрат отклонений индивидуальных значений признака от их средней величины. В зависимости от исходных данных дисперсия может вычисляться по простой (6.4) или взвешенной (6.5)формуле: Дисперсией называется средний квадрат отклонений индивидуальных значений признака от их средней величины. В зависимости от исходных данных дисперсия может вычисляться по простой (6.4) или взвешенной (6.5)формуле:
 ; (6.4) ; (6.4)
 . (6.5) . (6.5)
Дисперсия – это один из наиболее распространенных в экономической практике обобщающих показателей размера вариации в совокупности. Дисперсию используют не только для оценки вариации, но и для измерения связей между исследуемыми факторами; распределение дисперсии на составляющие позволяет оценить влияние разных факторов, которые обусловливают вариацию признака.
 Среднее квадратическое отклонение – это обобщающая характеристика размеров вариации признака в совокупности. Оно показывает, насколько в среднем отклоняются конкретные варианты от их среднего значения; является абсолютной мерой колеблемости признака. Среднее квадратическое отклонение – это обобщающая характеристика размеров вариации признака в совокупности. Оно показывает, насколько в среднем отклоняются конкретные варианты от их среднего значения; является абсолютной мерой колеблемости признака.
Среднее квадратическое отклонение (его называют также стандартным отклонением) представляет собой корень квадратный из дисперсии:
 ; (6.6) ; (6.6)
 . (6.7) . (6.7)
Техника вычисления дисперсии сложна, а при больших значениях вариант и частот может быть громоздкой. Расчеты можно упростить (используя свойства дисперсии) следующим образом:
1. По способу моментов (от условного нуля):
 , (6.8) , (6.8)
где h – величина интервала;
А – условный нуль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой.
2. Если А=0, дисперсия рассчитывается по формуле
 . (6.9) . (6.9)
В статистике используют условные моменты m1, m2, m3 и центральные моменты М2, М3, необходимые для расчета дисперсии и среднего квадратического отклонения.
3. Расчет дисперсии через моменты первого и второго порядка:
 , (6.10) , (6.10)
где момент первого порядка рассчитывается по формуле
 ; (6.11) ; (6.11)
момент второго порядка – по формуле
 . (6.12) . (6.12)
Для сравнения вариации одного и того же показателя в разных совокупностях (например, заработной платы двух рекламных агентств) или вариации разных показателей в одной совокупности (например, вариации заработной платы и возраста в одном рекламном агентстве) используют относительные показатели вариации. Базой для сравнения в относительных показателях служит средняя арифметическая величина. К относительным показателям относят:
 Относительный размах вариации (коэффициент осцилляции) Относительный размах вариации (коэффициент осцилляции)
 . (6.13) . (6.13)
 Относительное линейное отклонение (линейный коэффициент вариации) Относительное линейное отклонение (линейный коэффициент вариации)
 . (6.14) . (6.14)
 Коэффициент вариации Коэффициент вариации
 . (6.15) . (6.15)
Коэффициент вариации используют не только для сравнительной оценки вариации единиц совокупности, но и как характеристику однородности совокупности. Совокупность считается количественно однородной, если коэффициент вариации не превышает 33%.
 Пример 5. Имеются следующие данные о распределении сотрудников рекламного агенства по уровню оплаты труда, данные представлены в таблице 9 (данные условные). Определите абсолютные и относительные показатели вариации (для вычисления используйте данные примеров, рассмотренных выше). Пример 5. Имеются следующие данные о распределении сотрудников рекламного агенства по уровню оплаты труда, данные представлены в таблице 9 (данные условные). Определите абсолютные и относительные показатели вариации (для вычисления используйте данные примеров, рассмотренных выше).
Решение. Рассчитаем абсолютные и относительные показатели вариации. Дополнительные расчеты произведем в табл. 9.
Таблица 9
Группы сотрудников по уровню заработной платы,
тыс. р.
|
Число сотрудников (чел.)

|
Середина интервала

|

|

|

|
7-10
|
4
|
8,5
|
26,4
|
174,24
|
36
|
10-13
|
6
|
11,5
|
21,6
|
77,76
|
24
|
13-16
|
7
|
14,5
|
4,2
|
2,52
|
7
|
16-19
|
8
|
17,5
|
19,2
|
46,08
|
0
|
19-22
|
3
|
20,5
|
16,2
|
87,48
|
3
|
22-25
|
2
|
23,5
|
16,8
|
141,12
|
8
|
|
30
|
-
|
104,4
|
529,2
|
78
|
По расчетам примера 4 известно, что
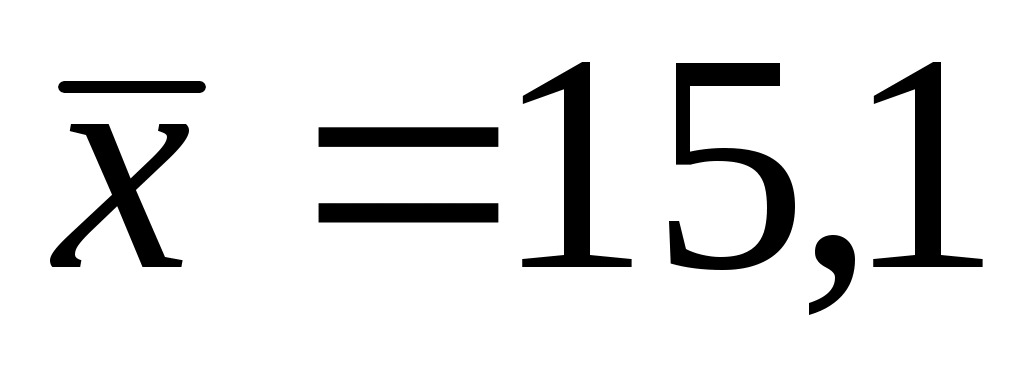 ; ;
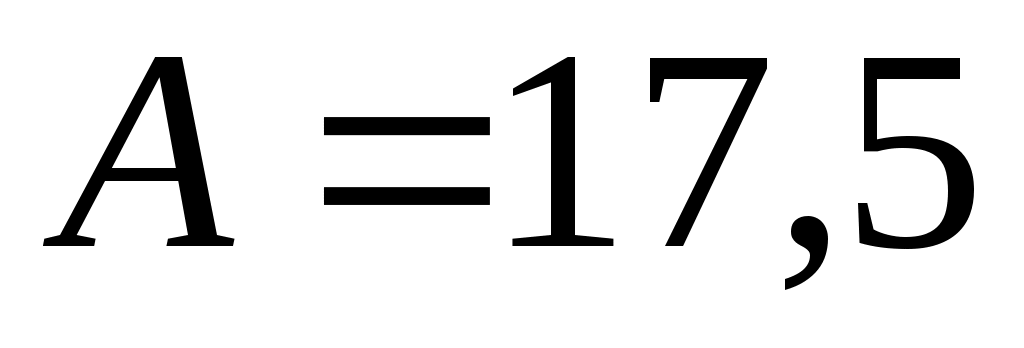 ; ;
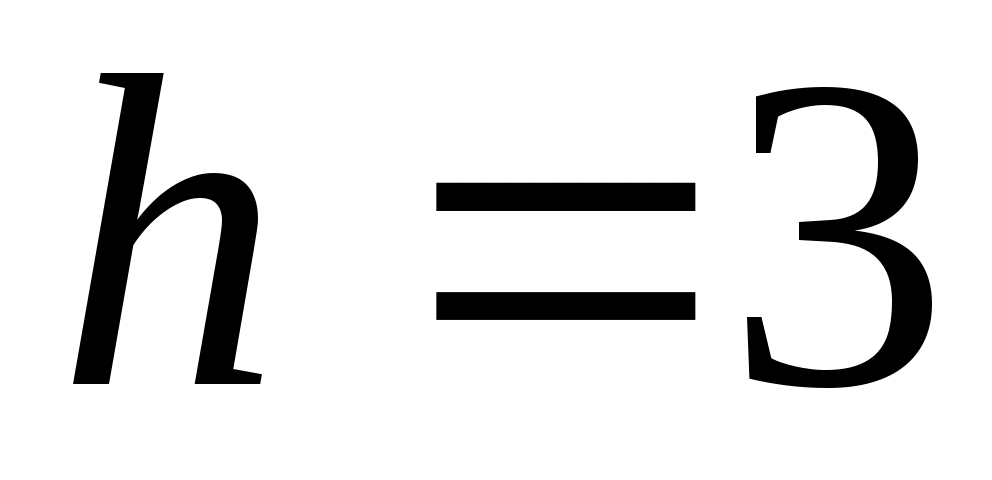 . .
Рассчитываем абсолютные показатели вариации:
Размах рассчитываем по формуле (6.1). В данном примере размах будет равен
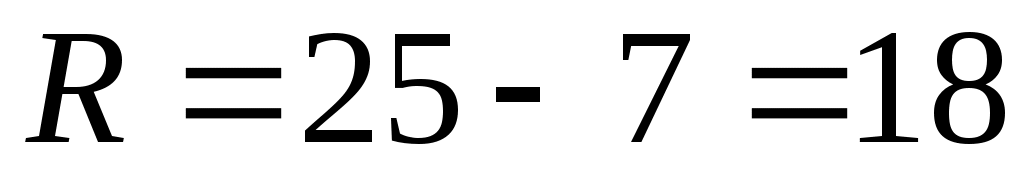 тыс. р. тыс. р.
Вывод. Величина размаха вариации показывает, что заработная плата сотрудников рекламного агенства изменяется (колеблется) в пределах от 25 до 7 тыс. р., а общая ширина диапазона принимаемых значений (амплитуда колебаний) составляет 18 тыс. р.
Среднее линейное отклонение рассчитывается по формуле (6.3):
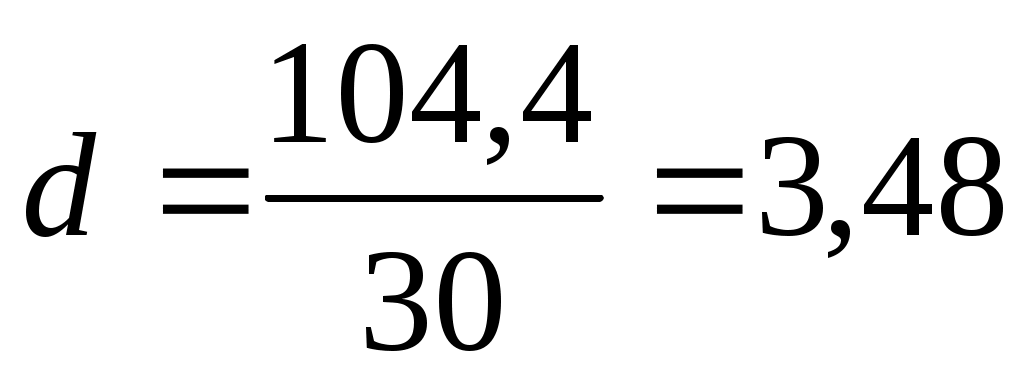 тыс. р. тыс. р.
Вывод. Данный показатель показывает, что в среднем конкретные варианты признака отклоняются от среднего значения на 3,48 тыс.р.
Рассчитаем дисперсию всеми способами:
Расчет дисперсии по классической формуле (6.5):
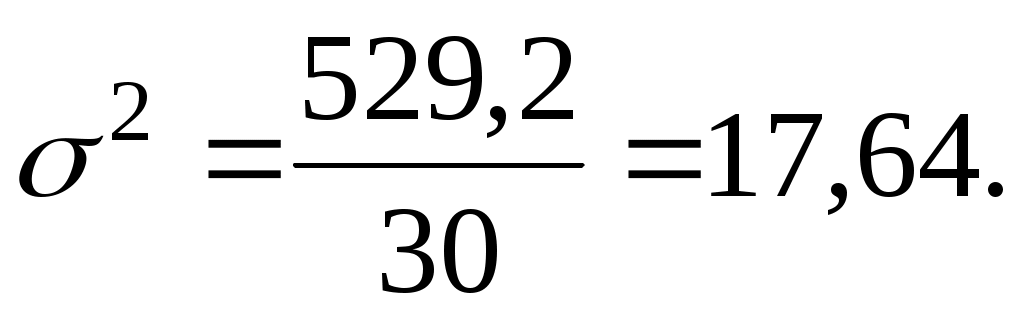
Расчет дисперсии по способу моментов (от условного нуля) по формуле (6.8):
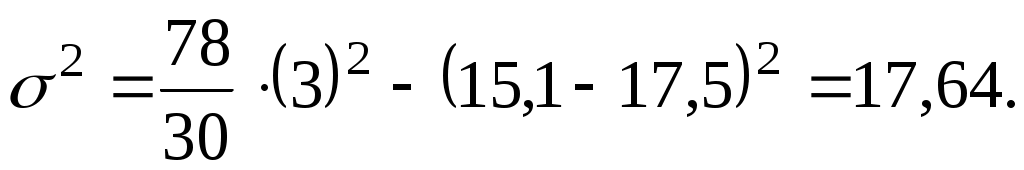
Расчет дисперсии через моменты первого и второго порядка по формуле (6.10):
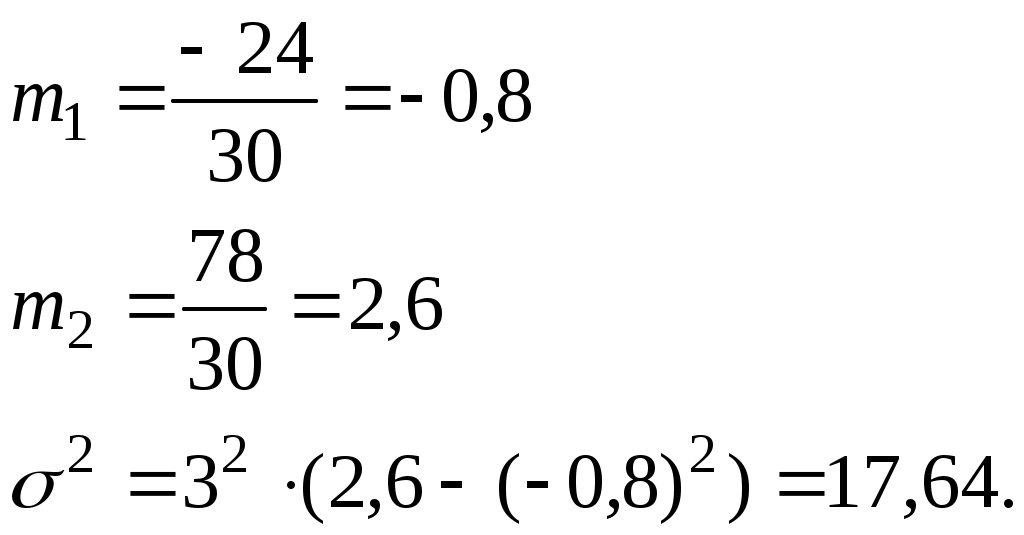
Вывод. Дисперсия, рассчитанная различными способами, составила 17,64. Данный показатель необходим для расчета среднего квадратического отклонения.
Рассчитаем среднее квадратическое отклонение по формуле (6.7):
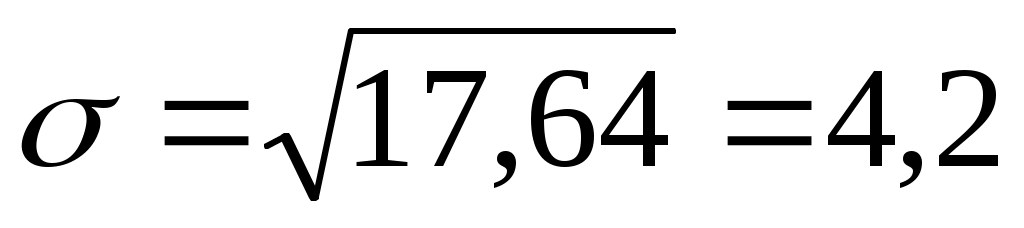 тыс.р. тыс.р.
Вывод. Рассчитанное среднее квадратическое отклонение показывает, что в среднем каждый сотрудник рекламного агенства получает заработную плату на 4,2 тыс. р. больше или меньше, чем средняя заработная плата, составляющая 15,1 тыс. р.
Рассчитываем относительные показатели вариации:
Коэффициент осцилляции рассчитаем по формуле (6.13):
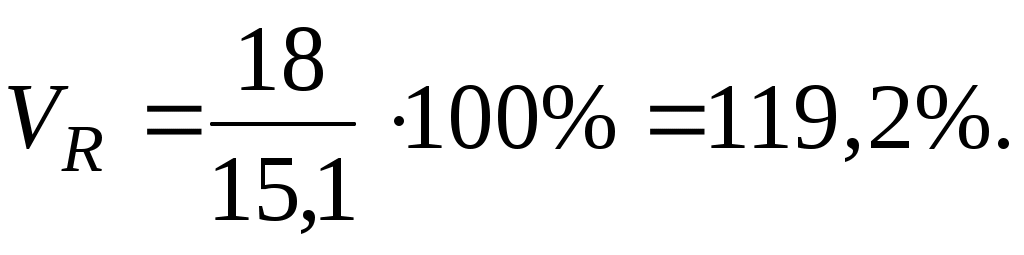
Линейный коэффициент вариации рассчитаем по формуле (6.14):
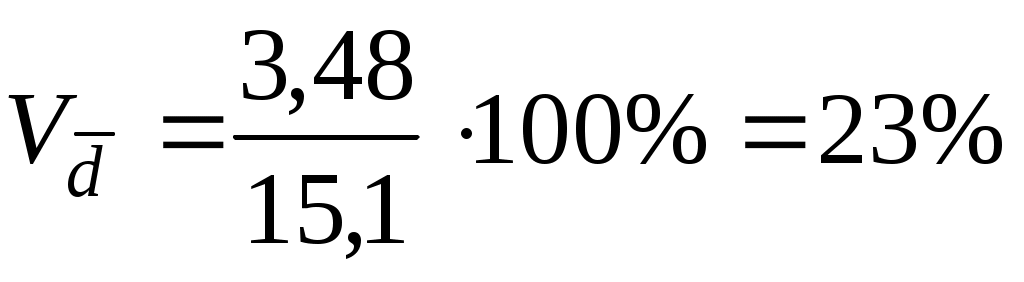 . .
Коэффициент вариации рассчитаем по формуле (6.15):
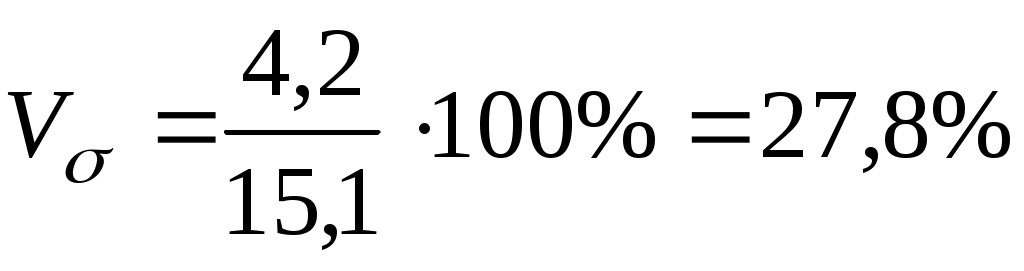 . .
Наиболее часто в практических расчетах из трех относительных показателей применяется коэффициент вариации.
Вывод: Значение данного показателя показывает, что сотрудники рекламного агенства однородны по уровню заработной платы, т.к. рассчитанный коэффициент вариации меньше 33% (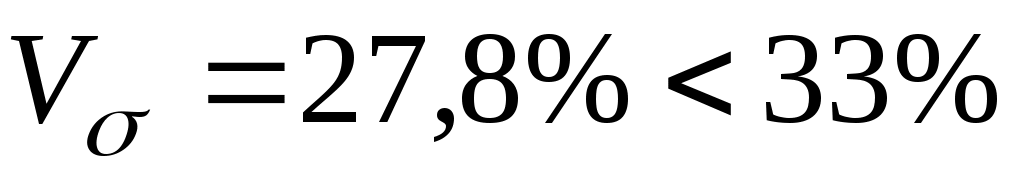 ). ).
|
|
|
 Скачать 3.39 Mb.
Скачать 3.39 Mb.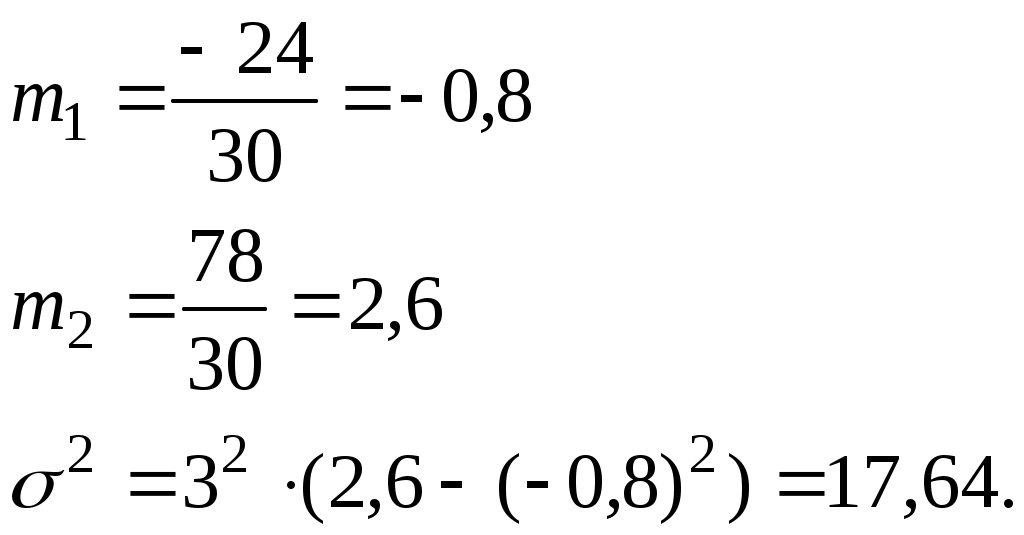

 (6.2)
(6.2) (6.3)
(6.3) ; (6.4)
; (6.4) . (6.5)
. (6.5) ; (6.6)
; (6.6) . (6.7)
. (6.7) , (6.8)
, (6.8) . (6.9)
. (6.9) ; (6.11)
; (6.11) . (6.12)
. (6.12)