урок математики. Учебник для учащихся общеобразовательных учреждений в 2 ч. В. Н. Рудницкая, Т. В. Юдачева. М. ВентанаГраф, 2010
 Скачать 2.65 Mb.
|
|
Задания № 8, 10 (с. 51–52). Способы рассуждений, рассматриваемые в этом задании, будут в дальнейшем основными при решении уравнений вида: 24 + х = 36 и 49 – х = 16. Поэтому надо не спеша и обстоятельно со всем классом прочитать текст учебника и в нем разобраться. Для закрепления можно предложить аналогичные упражнения, например: 1. Какое число «машина» прибавила? 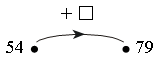 2. Какое число «машина» вычла?  Задание № 12 (с. 52). – Прочитайте текст. Можно ли его назвать задачей? – Прочитайте условие. – Найдите и прочитайте вопрос. – Запишите кратко условие задачи и решите ее. 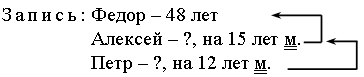 Решение: 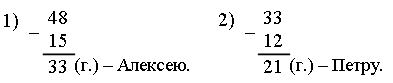 О т в е т: 33 года, 21 год. – Почему решали задачу вычитанием? Задание № 13 (с. 52). – Прочитайте задачу. – Что известно? Что требуется узнать? – Запишите кратко условие задачи. Запись: Всего – 95 уч. В кино – 30 уч. В музей – 23 уч. В театр – ? уч. – Решите задачу двумя способами по действиям. I способ. 1) 95 – 30 = 65 (уч.) – второклассников пошли на экскурсию и в театр; 2) 65 – 23 = 42 (уч.) – второклассника поехали в театр. II способ. 1) 30 + 23 = 53 (уч.) – второклассника пошли в кино и в музей; 2) 95 – 53 = 42 (уч.) – второклассника поехали в театр. О т в е т: 42 уч. Вместе с тем дети уже знакомились с новой для них формой записи решения – выражением, поэтому можно поставить перед ними дополнительное условие: использовать в качестве формы записи выражение. При этом слабым ученикам предложите в помощь следующую карточку: 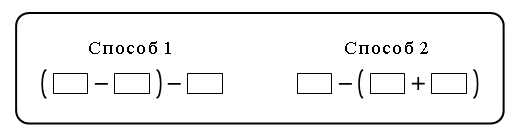  V. Повторение пройденного материала. 1. Работа по учебнику. Задание № 22 (с. 55). Это логическая задача. Перед выполнением этого задания учитель проводит с опорой на наглядность решение аналогичной ситуации. Учитель берет непрозрачный пакет и на глазах детей кладет в него, например, 2 яблока и 3 груши (или любые другие предметы разной формы, которые легко узнать на ощупь). Далее работа организуется так. Учащимся задаются вопросы: – Сколько в пакете груш и яблок? (3 груши и 2 яблока.) Давайте подумаем, сколько раз можно вытащить по одному фрукту, чтобы обязательно достать грушу? Смотрите, я вытаскиваю один фрукт. (Рука учителя в пакете.) Обязательно ли это груша? (Нет, так как в пакете не только груши, но и 2 яблока.) (Учитель вытаскивает яблоко.) Действительно, в первый раз я могу вытащить не грушу, а яблоко. Сколько груш и яблок теперь осталось в пакете? (3 груши и 1 яблоко.) Вытаскиваю фрукт второй раз. Как вы думаете, это обязательно груша? (Нет, так как в пакете остались не только груши, но и 1 яблоко.) (Учитель опять вытаскивает яблоко.) Второй раз я снова могу вытащить яблоко. Сколько груш и яблок осталось в пакете? (3 груши и ни одного яблока.) Буду вытаскивать в третий раз. Как вы считаете, это обязательно груша? (Да, так как в пакете яблок больше нет.) Делаем вывод: число возможных попыток у нас зависело не от числа груш, а от числа яблок. Учитель убирает яблоки в пакет. Перед детьми ставится проблема: – Сколько раз нужно вытащить по одному фрукту, чтобы обязательнодостать яблоко? (Ученики быстро сообразят, что число попыток в этом случае зависит не от числа яблок, а уже от числа груш.) (Так как в пакете 3 груши, то мы можем гарантировать, что только в четвертый раз обязательно достанем яблоко.) Теперь можно переходить к задаче, сформулированной в учебнике. Рассуждение аналогично. Выводы: 1. Так как конфет «Смородина» – четыре, то надо взять не меньше пяти конфет, чтобы обязательно вытащить «Малину». 2. Так как конфет «Малина» – пять, то надо взять не меньше шести конфет, чтобы обязательно вытащить «Смородину». 2. Работа в печатной тетради № 1. Задание № 85. – Прочитайте задачу. – Что известно? Что требуется узнать? – Запишите решение задачи по действиям. Оформить решение задачи в тетради учащиеся должны следующим образом: Решение: 1) 15 · 3 = 15 + 15 + 15 = 45 (гр.) – нашли.  2) 45 – 25 = (гр.) – пожарили. 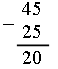 Ответ: 20 грибов. При выполнении первого действия учащиеся используют фишки. VI. Итог урока. – Что нового узнали на уроке? – Как выполнять сложение и вычитание двузначных чисел в столбик? – Какие единицы длины вы знаете? Домашнее задание: № 19 (учебник); № 80 (рабочая тетрадь). Урок 27 Сложение двузначных чисел (общий случай) Цели урока: рассмотреть общие приемы сложения двузначных чисел; совершенствовать навыки решения задач; развивать умение рассуждать и обобщать. Ход урока I. Организационный момент. II. Устный счет. 1. Чем похожи и чем отличаются друг от друга числа в каждой паре:
2. По какому правилу записан каждый ряд чисел: а) 90, 60, 70, 40, 50, 20, 30, 0, 10; б) 10, 30, 20, 40, 30, 50, 40, 60, 50. 3. Найдите значения выражений: 30 + 20 – 40 + 60 – 50 + 20 + 40 =  80 – 30 – 10 + 50 – 70 + 60 – 80 = 90 – 60 + 20 – 40 + 60 + 20 – 50 = 30 + 40 – 60 + 80 – 20 – 60 + 10 = 20 + 70 – 50 + 30 – 60 + 80 – 90 = 4. Сколько отрезков с отмеченными концами можно найти на этом рисунке? 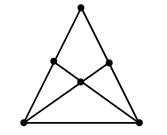 III. Сообщение темы урока. – Сравните выражения каждого столбика:
– Чем отличаются выражения первого столбика от выражений второго столбика? – Сегодня на уроке рассмотрим сложение двузначных чисел в пределах 100 с переходом через десяток. IV. Изучение нового материала. Подготовительные задания: 1) Назовите число, которое на 1 больше каждого из чисел: 6, 4, 8, 7, 0, 2, 9, 1, 5, 3. 2) Число 6 можно записать так:  . Какое число означает каждая из записей:  ?Примечание. Очень важно выработать у учащихся умение воспринимать подобные записи. Например, как запись числа 6, являющегося суммой 5 и 1. Во-первых, это предупредит весьма распространенную ошибку, допускаемую детьми: в тех случаях, когда при сложении единиц в результате получается число, большее 10, они, сложив десятки, забывают прибавлять к ним еще 1 десяток. Во-вторых, представляется возможность сократить число шагов алгоритма сложения, что тоже немаловажно для выработки скорости вычислений.Задание № 1 (с. 56). – Рассмотрите рисунок на с. 56 и объясните, как Волк и Заяц выполняли сложение вида 27 + 15. Один из учащихся рассказывает, что и как выполняют Волк и Заяц, а остальные дети работают параллельно, используя наборы оранжевых и белых палочек. Задача: найти сумму 27 и 15. Волк и Заяц составили «поезд» из 2 оранжевых и 7 белых «вагонов» и «поезд» из 1 оранжевого и 5 белых «вагонов». Затем к первому «поезду» они прицепляют слева один оранжевый, а справа – 5 белых «вагонов» из второго «поезда». Получился новый «поезд», в котором 3 оранжевых и 12 белых «вагонов». Но 12 – это 1 десяток и 2 единицы. Поэтому Волк и Заяц десяток белых «вагонов» заменили одним оранжевым «вагоном». Длина «поезда» не изменилась. Получилось 4 оранжевых и 2 белых «вагона». Поезд обозначает число 42. Значит, сумма 27 и 15 равна 42. Далее переходите к рассмотрению записи сложения этих чисел столбиком. 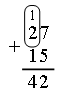 7 + 5 – двенадцать: 1 десяток (пишем маленькую цифру 1 над цифрой 2) и 2 единицы (пишем 2 под 5), 3 + 1 – четыре (пишем 4 под 1). Получается 42. В дальнейшем можно сократить рассуждение, сделать его более лаконичным. Рассмотрите со всем классом следующие примеры: Пример 1: сложить 64 и 29. 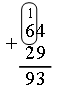 Объяснение: 4 + 9 – тринадцать: 1 десяток 3 единицы, 7 + 2 – девять. Сумма 93. Пример 2: сложить 75 и 6. 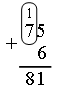 Объяснение: 5 + 6 – одиннадцать: 1 десяток 1 единица, 8 + 0 – восемь. Сумма 81. Пример 3: сложить 4 и 58. 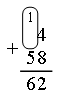 Объяснение: 4 + 8 – двенадцать: 1 десяток 2 единицы, 1 + 5 – шесть. Сумма 62. Задание № 2 (с. 57). Учащиеся работают в парах. Используя цветные палочки, они находят значение сумм с переходом через десяток. Задание № 3 (с. 57). Учащиеся выполняют задание с комментированием у доски, записывая сложение чисел в столбик. V. Повторение пройденного материала. 1. Работа в печатной тетради № 1. Задание № 85. Если у учащихся нет возможности воспользоваться калькулятором, то выполнить проверку они смогут с помощью цветных палочек, что подготовит второклассников к изучению следующей темы. Рассмотрим первый пример. Дети письменно выполняют вычисления и заполняют окошко. 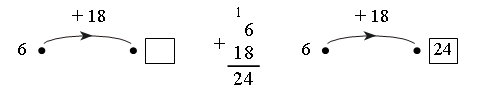 2. Работа по учебнику. Задание № 10 (с. 58). – Прочитайте текст. Является ли он задачей? Почему? – Что известно в задаче? Что требуется узнать? – Все ли необходимые данные есть в тексте? – Какие данные для решения задачи нужно взять из рисунка? – Рассмотрите рисунок. Выполните схему к условию задачи. 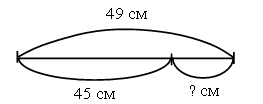 Решение: 49 – 45 = 4 (см). Ответ: 4 см. Задание № 11 (с. 58). – Прочитайте задание. – Какая команда одержала победу? (Команда «Вымпел».) – Сколько очков составила разница в счете? Какое действие необходимо выполнить? (Вычитание, так как узнаем, на сколько больше очков у одной команды, чем у другой.) Запись: 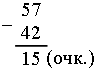 Задание № 12 (с. 58). – Рассмотрите рисунок. Какое действие надо выполнить, чтобы найти высоту второго этажа? Запись: 4 м 69 см – 2 м 35 см = 2 м 34 см. VI. Итог урока. – Что нового узнали на уроке? – Как выполнить сложение чисел с переходом через десяток? – Что означает запись:  ?Домашнее задание: № 8, 9 (учебник); № 83, 84 (рабочая тетрадь). Урок 28 Сложение двузначных чисел (общий случай) Цели урока: совершенствовать вычислительные навыки; продолжить формирование умений составлять задачи по иллюстрации и решать их; закреплять знания о многоугольниках; развивать умения анализировать и сравнивать. Ход урока I. Организационный момент. II. Устный счет. 1. Работа с калькулятором. – Наберите на калькуляторе любое двузначное число. – Подумайте, на сколько можно его увеличить, чтобы изменялась только цифра, обозначающая десятки, а цифра, обозначающая единицы, не изменялась? Проверьте свои предположения на различных числах. 2. Задача. – Чем похожи тексты задач? Чем отличаются? Какую задачу вы можете решить? Какую – нет? – Почему?
– Решите вторую задачу. 3. Какие числа нужно вставить в «окошки», чтобы получились верные равенства:
4. Сколько здесь треугольников? 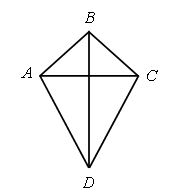 О т в е т: ∆АВС, ∆АВЕ, ∆ВСЕ, ∆ACD, ∆ADE, ∆CDE, ∆BCD, ∆ABD. III. Сообщение темы урока. – Сегодня мы продолжим закреплять навыки сложения двузначных чисел с переходом через десяток. IV. Работа над темой урока. Задание № 4 (с. 57). – Прочитайте математические записи, используя выражения: «сумма чисел», «разность чисел», «уменьшить на», «увеличить на». – Чем похожи все выражения? (В них есть скобки.) – Какое действие выполняется первым в выражении со скобками? – Проверьте, верно ли выполнены вычисления. Запись: (27 + 45) + 8 = 80 96 – (13 + 57) = 36 и т. д. 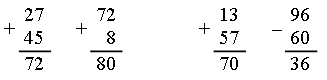 Задание № 5 (с. 57). – Что необходимо знать, чтобы установить стоимость покупки? – Все ли необходимые данные для этого содержатся в тексте? – Запишите кратко условие задачи и решите ее по действиям. Запись: 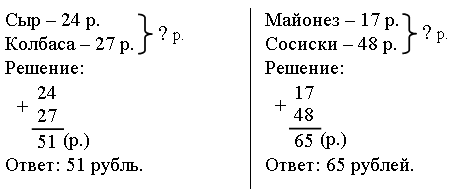  |