Хрестоматия. Петухов. Том 3. Книга 2. Учебник по общей психологии, предназначено для проведения семинарских занятий по данному курсу и самостоятельного чтения
 Скачать 20.88 Mb. Скачать 20.88 Mb.
|
|
С.Л. Рубинштейн ОСНОВНАЯ ЗАДАЧА И МЕТОД ПСИХОЛОГИЧЕСКОГО ИССЛЕДОВАНИЯ МЫШЛЕНИЯ1 Основная задача психологического исследования мышления заключается в том, чтобы, не ограничиваясь фиксацией внешних результатов мыслительной деятельности, вскрыть самый процесс мышления во внутренних закономерностях его протекания. Это — генеральная линия. Она реализуется в отношении ряда проблем, где исследование умственной деятельности сводилось к описанию ее внешнего протекания, к констатации фактов, в которых она выражается, без раскрытия внутреннего закономерного процесса, приводящего к этим фактам. Показательным примером может служить проблема «переноса». В педагогической практике учитель часто встречается с тем, что ученик, решивший задачу или как будто усвоивший теорему применительно к данным условиям, оказывается не в состоянии «перенести» это решение в другие условия, решить ту же задачу, как только задача предъявляется ему в видоизмененных условиях. Это часто встречающийся и практически фундаментально важный факт. С констатации подобных фактов начинает, как известно, свое исследование о «продуктивном мышлении» Вертгеймер. На нем останавливались и авторы ряда исследований, публиковавшихся в нашей психологической литературе. Чрезвычайно важно поэтому выяснить его причины. Под переносом обычно разумеют применение сложившегося у индивида и закрепленного в виде навыка способа действия в новых условиях, при решении других аналогичных задач. Однако и закрепляющийся в виде навыка способ решения задачи должен быть сперва найден. Поэтому в конечном счете в плане мышления проблема «переноса» пре- 1 Хрестоматия по общей психологии. Психология мышления / Под ред. Ю.Б.Гиппен-рейтер, В.В.Петухова. М.: Изд-во Моск. ун-та, 1981. С. 281-288. 558 Тема 18. Экспериментальные исследования мышления образуется в проблему применения прежде найденных решений (знаний) к новым задачам. За фактами отсутствия переноса решения с одной задачи на другую, ей аналогичную, стоит недостаточный анализ условий задачи соотносительно с ее требованиями и вытекающая отсюда недостаточная обобщенность решения. Условия, в которых дается задача, включают обычно в более или менее нерасчлененном виде собственно условия задачи, т.е. те данные, которые участвуют в решении, с которым это последнее необходимо связано, и ряд привходящих обстоятельств (то или иное расположение чертежа, та или иная формулировка задачи и т.п.). Для того чтобы решение задачи оказалось для учащегося (испытуемого) переносимым на другие случаи, отличающиеся от исходных лишь несущественными, привходящими обстоятельствами (тем или иным расположением фигур и т.п.), необходимо (и достаточно), чтобы анализ через соотнесение с требованиями задачи вычленил собственно условия задачи из различных привходящих обстоятельств, в которых они непосредственно выступают сначала. Невозможность переноса решения в другую ситуацию (при изменении положения фигуры и т.п.) объясняется отсутствием такого анализа и отсюда вытекающей недостаточной обобщенностью решения задачи. Мало того, чтобы реализовать даже обобщенное решение в новых обстоятельствах, нужно не просто его «перенести», а, сохраняя его по существу, соответственно соотнести его с этими обстоятельствами, т.е. проанализировать и их (иногда через это соотнесение осуществляется и самое обобщение решения, выступающее в этом случае как результат синтетического акта). В основе переноса лежит обобщение, а обобщение есть следствие анализа, вскрывающего существенные связи. Анализа требуют как сама задача, условия, в которых она первоначально решается, так и те видоизмененные условия, на которые это решение переносится. С переносом решения одной и той же задачи в разные условия (обстоятельства) тесно связан перенос решения из одной задачи на другую, однородную с ней в том или ином отношении. Этот последний случай был подвергнут у нас специальному исследованию. Опыты К.А.Славской показали, что перенос совершается в том и только в том случае, когда обе задачи соотносятся и включаются испытуемыми в процессе единой аналитико-синтетической деятельности. Конкретно это выражается в том, что условия одной задачи анализируются через их соотнесение с требованиями другой. Для осуществления переноса решения требуется обобщение, связанное с абстракцией от несущественных моментов первой задачи и конкретизацией его применительно ко второй. Главную роль при переносе играет анализ основной задачи, подлежащей решению. Течение процесса обобщения и осуществление переноса зависят главным образом от степени проанализированности той основной задачи, Рубинштейн С.Л. Основная задача и метод... 559 на которую должен быть совершен перенос. Если вспомогательная задача предъявлялась на начальных этапах анализа основной, то она решалась сперва самостоятельно, безотносительно ко второй; обобщение совершалось в результате развернутого соотнесения свойств и отношений обеих задач. Если вспомогательная задача предъявлялась, когда анализ основной задачи был уже значительно продвинут, то вспомогательная задача решалась сразу через соотнесение с требованиями основной, как звено этой последней. В этом случае обобщение совершается в ходе решения вспомогательной задачи. Поэтому нет нужды в специальном применении одной задачи к другой: перенос осуществляется с места, сразу. Эксперимент, в ходе которого это вскрылось, велся следующим образом: экспериментатор предлагал испытуемому решить задачу, рассуждая вслух: ход рассуждений испытуемого при решении задачи подробно протоколировался. Испытуемым — учащимся 7-9-х классов средних школ — давалась основная задача: доказать равновеликость треугольников АВО и OCD, заключенных между диагоналями трапеции (решение ее заключается в выделении треугольников ABD и ACD, которые равновелики, так как имеют общее основание AD и общую высоту трапеции; искомые треугольники являются частью данных и поэтому равновелики) (рис. 1). Для исследования переноса решения с одной задачи на другую испытуемым в ходе решения одной (основной) задачи давалась другая, вспомогательная. В экспериментальную группу включались только те из обследованных испытуемых (48 школьников и 12 студентов), которые решали основную задачу с помощью вспомогательной и на которых поэтому можно было прослеживать ход переноса. Во вспомогательной задаче нужно было доказать равенство диагоналей прямоугольника ABCD. Они равны, так как равны треугольники ABD и ACD, имеющие общее основание AD, равные стороны АВ и CD и равные прямые углы (рис. 2). Основная задача решается с помощью вспомогательной посредством переноса на нее решения вспомогательной задачи. Общим звеном в решении обеих задач было использование общего основания AD треугольников ABD и ACD, которое в одном случае используется как общее основание равных, в другом — равновеликих треугольников. Таким образом, чтобы решить основную задачу, т.е. найти равновеликие фигуры, связанные с искомыми и имеющие равные (общие) высоты и общее основание, нужно выделить это звено решения вспомогательной задачи как общее для обеих задач, т.е. произвести обобщение. Чтобы проследить зависимость обобщения от анализа основной задачи, вспомогательная задача предъявлялась испытуемым на разных этапах анализа основной. 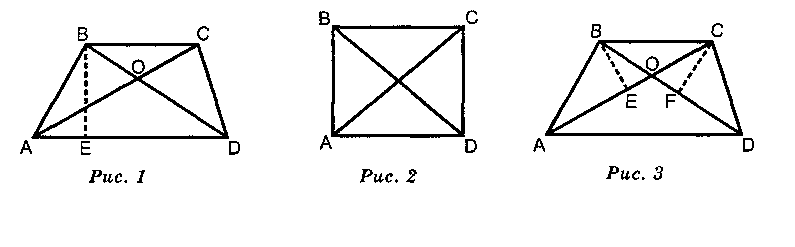 560 Тема 18. Экспериментальные исследования мышления В качестве ранних этапов в специальном, узком смысле слова мы выделяли те, на которых испытуемые оперировали, анализировали и т.д. лишь с тем, что было непосредственно дано в условиях задачи; под поздними этапами анализа мы соответственно разумели те стадии решения задачи, на которых испытуемые уже выделяли новые условия, выходящие за пределы того, что было непосредственно дано в исходных условиях задачи. Конкретно различение более ранних и более поздних этапов анализа основной задачи в наших экспериментах осуществлялось следующим образом. Одной части испытуемых вспомогательная задача давалась в тот момент, когда они анализировали непосредственно данные в задаче условия, т.е. на ранних этапах анализа задачи. Эти испытуемые проводили высоты треугольников АВО и OCD и анализировали их равновели-кость, т.е. пытались доказать равенство их высот и оснований (рис. 3). Вначале, следовательно, они анализировали то, что непосредственно дано в условии задачи — равновеликость треугольников АВО и OCD. В ходе проб испытуемые убеждались в невозможности доказать равновеликость АВО и OCD через равенство их высот и оснований. Они продолжали анализировать задачу дальше, выявляли новые, не данные им условия. Так, они выделяли другие фигуры, связанные с искомыми, чтобы первоначально доказать их равновеликость, рассматривали их высоты и основания (например, треугольников ABD и BCD с общей высотой трапеции и основаниями, которые являются верхним и нижним основаниями трапеции). Это выделение в ходе анализа задачи новых условий мы принимали за поздние этапы анализа задачи. Второй группе испытуемых вспомогательная задача предъявлялась на этих поздних этапах анализа основной. Чтобы «перенести» решение с одной задачи на другую, нужно найти обобщенное решение обеих задач. Предъявляя вспомогательную задачу на разных этапах анализа основной задачи, мы прослеживали, как осуществляется обобщение в зависимости от степени проанализированно-сти основной задачи, зависимость обобщения от анализа. Испытуемые первой группы, которым вспомогательная задача предъявляется на ранних этапах анализа основной, решают вспомогательную задачу как самостоятельную, не связанную с основной. После решения вспомогательной задачи испытуемые возвращались к решению основной задачи. При этом большая часть испытуемых начала соотносить дальнейшее решение основной задачи со вспомогательной. Таким образом, получается, что начальные этапы, или низшие уровни мышления, сами создают предпосылки, которые ведут к высшим. «Мотивом», побуждавшим к этому соотнесению, служило то, что испытуемые уже до осуществления сколько-нибудь развернутого и углубленного соотнесения задач усматривали, что между обеими задачами есть что-то общее, раскрывающееся затем в результате этого соотнесения, так как никаких указаний на связь обеих задач испытуемым не Рубинштейн С.Л. Основная задача и метод... 561 давалось; более того, чтобы не наводить испытуемых на эту мысль, экспериментатор предъявлял вспомогательную задачу с нарочито маскировочной установкой, говоря испытуемым, что вторая вспомогательная задача дается им для передышки. Следовательно, оказывается, что сам ход решения задачи создает внутренние условия для дальнейшего движения мысли, причем эти условия включают в себя не только предпосылки логически-предметные, но и мотивы мышления, «двигатели» его. Соотнесение (синтез) задач осуществлялось так, что, продолжая решение основной задачи, испытуемые анализировали в ней те же геометрические элементы (углы, равные стороны, равные диагонали), которые они использовали при решении вспомогательной задачи. Так, например, испытуемый Д.В. говорит: «Здесь же трапеция — совсем другое дело. Здесь диагонали не равны и боковые стороны тоже. Я не знаю, чем мне здесь могут помочь диагонали...» (протокол № 17). Протоколы показывают, что, анализируя условия основной задачи, испытуемые выделяют элементы, использовавшиеся во вспомогательной задаче, для доказательства равенства треугольников. Все испытуемые анализируют в условиях основной задачи общие, сходные со вспомогательной задачей условия. Условия основной задачи анализируются через соотнесение с требованием вспомогательной. Испытуемый Д.В. говорит: «Мне нужно доказать равновеликость треугольников». Испытуемый переходит к анализу новых условий, убеждаясь в невозможности использовать для решения данные в условии задачи треугольники. «Очевидно, что прямо и через равенство данных треугольников доказать нельзя, — говорит он, — может быть, можно через треугольники ABD и ACD?». Так испытуемый Д. В. переходит к выявлению новых условий основной задачи. Это создает предпосылки для привлечения новых условий из вспомогательной задачи (через соотнесение с требованием основной). Из всех найденных в ходе предшествующего анализа геометрических элементов (равных сторон, диагоналей и т. д.) привлекается к решению основной задачи только общее основание AD — для доказательства равновеликости треугольников ABD и ACD. Испытуемый Д. В. говорит: «Равенство углов нам не нужно, равенство диагоналей тоже не нужно, а общее основание мы можем использовать». Таким образом, испытуемый выявляет то общее звено решения, которое является существенным и для основной задачи. Происходит обобщение — в геометрическом элементе, использовавшемся при решении вспомогательной задачи (для доказательства равенства), выявляется новое свойство, существенное с точки зрения требования основной задачи (для 562 Тема 18. Экспериментальные исследования мышления доказательства равновеликости треугольников). Таким образом, оказывается, что ни одно из звеньев решения вспомогательной задачи не привнесено извне в основную задачу; каждое звено решения основной задачи оказывается выявленным в результате анализа самой основной задачи, ее условий, ими обусловленных отношений ее элементов, поэтому оно выделяется как общее, т.е. отвечающее требованию основной задачи, т.е. существенное для нее. Так происходит движение анализа от выявления общего как сходного к выделению общего, существенного для основной задачи. Итак, при предъявлении вспомогательной задачи на ранних этапах анализа основной испытуемые первой группы решают вспомогательную задачу как самостоятельную, не связанную с основной. Обобщение совершается постепенно в ходе дальнейшего анализа основной задачи, осуществляющегося через соотнесение сначала с требованием вспомогательной, затем основной задачи. Движение процесса совершается от выявления сходного к выделению существенного через анализ и соотнесение обеих задач. Вторая группа испытуемых, которая получила вспомогательную задачу на поздних этапах анализа основной задачи, решала вспомогательную задачу не как самостоятельную, а как непосредственное продолжение основной. Так, например, решая вспомогательную задачу, где надо доказать равенство диагоналей, рассмотрев равенство треугольников, испытуемая Л.Г. говорит: «Они равны, т.е. у них общее основание, АВ и CD — общие высоты» (протокол № 16). Таким образом, испытуемая абстрагировалась от всех моментов (равенство углов и треугольников), которые были несущественны для основной задачи, где речь шла не о равенстве, а о равновеликости. Вместе с тем те прямые, которые во вспомогательной задаче являются сторонами, она обозначает как равные высоты и общее основание, т.е. сразу выделяет их в связи с основной задачей, связывает их и с доказательством равенства (как того требовала вспомогательная задача), и с доказательством равновеликости (в соответствии с требованием основной задачи). Испытуемая Л.Г. анализирует условия вспомогательной задачи не только через соотнесение с ее собственным требованием, но и одновременно с требованием основной задачи. В этом случае обобщение совершается уже в ходе решения вспомогательной задачи. Решение вспомогательной задачи служит как бы ответом на основную задачу, включается как недостающее звено анализа в решении последней. Обобщение совершается с «места», сразу, и нет необходимости в специальном действии применения одной задачи к другой. Это говорит о том, что именно обобщение, совершающееся при решении вспомогательной задачи, составляет истинную сущность того, что обозначается как перенос решения из задачи в задачу. Таким образом, при предъявлении вспомогательной задачи на поздних этапах анализа основной вспомогательная задача решается испытуемыми второй группы уже не как самостоятельная, а в связи с основной. Условия вспомогательной задачи анализируются через соотнесение с тре- Рубинштейн С.Л. Основная задача и метод… 563 бованием основной задачи, а не только через соотнесение с ее собственным требованием. В силу того, что основная задача проанализирована испытуемыми до предъявления вспомогательной, они сразу выделяют одно из звеньев решения вспомогательной задачи как существенное для основной задачи: обобщение совершается сразу в ходе решения вспомогательной задачи. Таким образом, сравнивая результаты экспериментов, проведенных с двумя группами испытуемых (получившими вспомогательную задачу на ранних и на поздних этапах анализа основной), можно сказать следующее. От степени проанализированности основной задачи зависит то, как конкретно совершаются обобщение и перенос, к которому приводит обобщение: развернуто, постепенно, в результате анализа элементов и отношений обеих задач или уже в ходе решения вспомогательной задачи «с места», сразу. Следовательно, от анализа основной задачи зависит, когда и как совершается обобщение. Это говорит о зависимости обобщения от анализа. Ход анализа основной задачи определяет, как совершится обобщение задач. Однако, как видно из рассмотренного экспериментального материала, обобщение подготовляется не в ходе анализа одной только основной задачи. Анализ того же экспериментального материала выявил также, что основным условием обобщения является включение обеих задач в единую аналитико-синтетическую деятельность. Только единая аналитико-синтетическая деятельность, включающая обе задачи, приводит к выделению общих звеньев, т.е. к переносу. Эта закономерность была не среднестатистической, а всеобщей закономерностью. Она выступила у всех без исключения 38 испытуемых, которым вспомогательная задача предъявлялась после основной, так же как и у всех 10, которым она предъявлялась до основной задачи. Та же закономерность, полученная сначала на основной группе испытуемых (школьников), проявилась и у 12 студентов, с которыми для сравнения проводились те же эксперименты. <...> Исследование наше показало, что, как уже отмечалось, продуктивное соотнесение вспомогательной задачи с основной совершается только на поздних этапах анализа последней. Это положение имеет, с нашей точки зрения, принципиальное значение, поскольку оно, по существу, означает, что использование «подсказки», заключенной во вспомогательной задаче, может быть совершено лишь тогда, когда анализ самой подлежащей решению задачи создал для этого внутренние условия. Между тем это положение вступило как будто бы в противоречие с данными другого нашего исследования, проводившегося Е.П.Кринчик. В ее экспериментах широко и систематически использовалось предъявление испытуемым, затруднявшимся в решении поставленной перед ними задачи, задач вспомогательных. В опытах Кринчик вспомогательные задачи предъявлялись испытуемым как до, так и после предъявления основной. Помимо этих экспериментальных данных и теоретические соображения 564 Тема 18. Экспериментальные исследования мышления как будто говорят за то, что предъявление вспомогательной, наводящей задачи, с которой решение переносится на основную, является важнейшим, привилегированным, основным, так как именно с этим случаем мы имеем дело при использовании прошлого опыта. Однако эти результаты экспериментов Е.П.Кринчик находятся в прямом противоречии с данными других исследований (Я.А.Пономарева, Ю.Б.Гиппенрейтер), согласно которым предъявление наводящей задачи оказывалось эффективным только при предъявлении ее после основной. Из разнобоя всех этих противоречивых данных мы делаем прежде всего один вывод, вытекающий из сформулированных выше общих положений, которые нашли себе подтверждение в ряде экспериментальных данных: вообще не существует и не может существовать никакой непосредственной однозначной зависимости между тем, когда испытуемому предъявляется вспомогательная задача, и эффектом, который ее предъявление дает. Как только, не оставаясь на внешней поверхности явлений, мы переходим к анализу и внешних, и внутренних соотношений, в каждом из разноречивых как будто случаев все сходится, выступает единая, общая для них всех закономерность. Зависимость решения от момента соотнесения обеих задач испытуемым выявляет роль внутренних условий, зависимость же решения от момента предъявления вспомогательной задачи до или после основной обнаруживает роль внешних условий. Конкретный анализ различных случаев предъявления вспомогательной задачи мог бы выявить, от чего зависят относительные преимущества ее предъявления в одних случаях до основной задачи, в других — после. Но мы уже видели, что предъявленная до основной вспомогательная задача может быть соотнесена с основной на поздних этапах анализа последней и потому окажется эффективной; она может быть предъявлена после предъявления основной, и соотнесение ее может произойти на ранних стадиях решения основной задачи, когда еще не созданы внутренние условия для продуктивного использования вспомогательной задачи, и оказаться неэффективным. Самый общий и важнейший вывод, который может быть сделан из этого анализа, заключается в том, что, ограничиваясь внешними данными (например, временем предъявления задачи и т.п.), нельзя прийти ни к каким однозначным результатам в отношении мышления и его закономерностей. Для этого необходимо вскрыть стоящий за этими внешними данными внутренний процесс и закономерные отношения, которые складываются в нем. Таким образом, в анализе задачи, подлежащей решению, заключены внутренние условия использования при ее решении других задач и любых «подсказок». Поэтому предъявляемые в ходе эксперимента вспомогательные задачи — точно дозируемые подсказки и т.п. — могут служить объективным индикатором внутреннего хода мысли, ее продвижения в решении задачи. |
