Хрестоматия. Петухов. Том 3. Книга 2. Учебник по общей психологии, предназначено для проведения семинарских занятий по данному курсу и самостоятельного чтения

• Название: Учебник по общей психологии, предназначено для проведения семинарских занятий по данному курсу и самостоятельного чтения
• Анкор: Хрестоматия. Петухов. Том 3. Книга 2.doc
• Дата: 22.09.2018
• Размер: 20.88 Mb.
• Имя файла: Хрестоматия. Петухов. Том 3. Книга 2.doc
• Тип: Учебник; #24954
• страница: 2 из 53

4. Фурье-анализ зрительного восприятия.

Часть 2. Факты, закономерности и результаты исследований восприятия

1. Восприятие цвета. Основные субъективные характеристики цвета и их объективные корреляты. Адаптация. Явление Пуркинье. Виды кон­трастов. Законы смешения цветов. Цветовой круг и треугольник. Цве­товое тело. Теории цветового зрения.

2. Восприятие пространства. Признаки удаленности и глубины: окуломо-торные, монокулярные (изобразительные), трансформационные, бино­кулярные. Механизмы стереозрения: диспаратность, теоретический и эмпирический гороптер, зона Панума, стереограммы Юлеша.

3. Восприятие движения. Системы восприятия реального движения: изоб­ражение/сетчатка и глаз/голова. Теории восприятия стабильности ви­димого мира. Иллюзии восприятия движения: автокинетическое, стро­боскопическое и индуцированное движение, эффект водопада. Восприя­тие времени.

4. Константность восприятия. Определение, виды, процедура измерения, коэффициент константности. Ядер-контекстная теория. Связь констан­тности восприятия величины с признаками удаленности. Теория пер­цептивных уравнений. Инвариантные отношения в восприятии.

5. Экспериментальные исследования восприятия пространства, движения и константности восприятия в рамках экологической теории. Поня­тие зрительной кинестезии.

6. Предметность восприятия. Виды оптических искажений. Исследования перцептивной адаптации к инвертированному зрению. Феномены псев-доскопического восприятия: их описание и объяснение. Правило правдо­подобия. Создание искусственных органов чувств и формирование у сле­пых «кожного зрения».

7. Установка в восприятии. Потребности и ценности как организующие факторы восприятия: экспериментальные исследования в школе «Но­вый взгляд». Кросс культурные исследования восприятия: особенности восприятия двумерных изображений в отдельных культурах.

8. Экспериментальная психология восприятия и изобразительное искусство.

Часть 1. Основные положения психофизики

1. Пороги ощущений. Чувствительность. Субсенсор­ный диапазон. Методы измерения порогов. Косвен­ное измерение ощущений. Закон Фехнера

Т. Энген

ОСНОВНЫЕ МЕТОДЫ ПСИХОФИЗИКИ¹

Сам Фехнер предложил три психофизических метода, которые вош­ли в психологию под именем основных методов. В литературе описываются и многие другие методы, но обычно они являются модификациями одного из этих трех методов. Эти основные методы сходны в одних отношениях и весьма различны в других. Все эти методы могут быть использованы для определения понятий, о которых шла речь выше. Выбор того или иного метода чаще всего зависит от двух практических и технических соображе­ний: 1) характер континуума стимулов, т.е. могут ли стимулы изменяться непрерывно (или по крайней мере очень малыми шагами) или же они мо­гут быть предъявлены только в дискретном виде. Использование дискрет­ного предъявления стимулов необходимо, например, при изучении вкуса и обоняния; 2) характер организации стимуляции, например, одновремен­ное или последовательное предъявление пар стимулов. В этом смысле при исследовании зрения мы располагаем большей свободой, чем при исследо­вании слуха. Сначала очень коротко, а затем более подробно рассмотрим основные психофизические методы.

1. Метод границ (едва заметных различий, минимальных изменений или серийного исследования). Это самый прямой метод определения поро­га. При определении разностного порога экспериментатор изменяет срав­ниваемый стимул малыми шагами в восходящих и нисходящих рядах. Испытуемый при каждом изменении стимула должен сказать, меньше, равен или больше переменный стимул по сравнению со стандартным. В результате эксперимента определяются значения переменного стимула, соответствующие смене категории ответа. При определении абсолютного порога стандартный стимул не предъявляется и задача испытуемого состо­ит в том, чтобы отвечать, обнаруживает он стимул или нет.

¹ Проблемы и методы психофизики / Под ред. А.Г.Асмолова, М.Б.Михалевекой. М.: Изд-во Моск, ун-та, 1974. С. 107-116, 119-130.

12

Тема 17. Экспериментальные исследования восприятия

2. 
   Метод установки (средней ошибки, воспроизведения или метод подравнивания). При определении разностного порога испытуемый, как правило, сам подстраивает сравниваемый стимул, который может непре­рывно изменяться, к стандарту, т.е. устанавливает такое значение пере­менного стимула, при котором он кажется равным стандарту. Эта проце­дура повторяется несколько раз, а затем вычисляется среднее значение и вариабельность установок испытуемого. Среднее значений подравниваний (установок) является прямым показателем точки субъективного равенства, а вариабельность подравниваний, допускаемая испытуемым, может быть использована для вычисления разностного порога. При определении абсо­лютного порога испытуемый неоднократно устанавливает такое значение переменного стимула, которое по его мнению является самым низким сре­ди обнаруживаемых им стимулов. Среднее этих установок принимается за абсолютный порог.
   
3. 
   Метод постоянных раздражителей (метод истинных и ложных случаев или метод частот). В этом методе используется несколько постоян­ных дискретных значений сравниваемого стимула. При определении раз­ностного порога каждое из них сравнивается со стандартным стимулом много раз. Для каждого из значений сравниваемого стимула подечитывается относительная частота разных ответов, например, ответов «меньше» и «больше». Если в опыте используются только две категории ответов, то испытуемый будет давать правильный ответ в половине случаев даже при одном только угадывании. Поэтому его разностный порог определяется как приращение или уменьшение величины сравниваемого стимула отно­сительно стандартного, правильно оцениваемое им в 75% проб, т.е. посре­дине между 50% (случайная удача) и 100%. Это значение, соответствую­щее 75%, определяется интерполяцией или каким-либо другим из не­скольких возможных статистических методов. Когда добавляется третья категория ответов типа «равно», «сомнительно» и тому подобное, метод постоянных раздражителей становится очень похож на метод границ. Ме­тод постоянных раздражителей может быть использован также для изме­рения абсолютного порога. В этом случае стандартный раздражитель не применяется, а за абсолютный порог принимают такое значение сравнива­емого стимула, который вызывает равное число ответов «да» и «нет».
   

Метод границ Абсолютный порог

Процедура опыта и вычисления при определении нижнего порога высоты звука методом границ показаны в табл. 1 (взята у Титченера¹).

¹ См.: TitchenerE.B. Experimental Psychology. N.Y. Macmillan, 1905. Vol. II. Quantitative.

Энген Г. Основные методы психофизики

13

Испытуемый получает инструкцию отвечать «да», когда он слышит тон, и «нет», когда он его не слышит в течение определенного интервала вре­мени, указываемого экспериментатором. Перед основным опытом следу­ет провести несколько предварительных тренировочных проб, чтобы убе­диться, что испытуемый усвоил процедуру опыта. Словесные инструкции трудно сделать краткими и ясными и часто они дают худшие результа­ты, чем предварительная тренировка.

В первом столбце табл. 1 (читать сверху вниз) указаны ответы испы­туемого на стимулы, предъявляемые в нисходящем ряду. Экспериментатор начинает этот ряд со сравниваемого стимула, равного 24 Гц и испытуемый отвечает «да». В каждой следующей пробе экспериментатор уменьшает частоту переменного стимула на 1 Гц, испытуемый продолжает давать по­ложительный ответ до тех пор, пока частота переменного стимула не ста­новится равна 14 Гц; тогда испытуемый отвечает «нет». Итак, порог лежит между 14 и 15 Гц. За порог принимается средняя точка — 14,5 Гц и эта

¹? — «сомневаюсь» считается как изменение категории ответа.

14 Тема 17. Экспериментальные исследования восприятия

величина L¹записывается под первым столбцом как одно из значений аб­солютного порога. Затем экспериментатор предъявляет стимулы в восхо­дящем ряду, начиная с 10 Гц, т.е. значительно ниже только что изме­ренного порога и получает ответ «нет». Экспериментатор увеличивает час­тоту переменного стимула снова на 1 Гц в каждой пробе и получает положительный ответ при частоте 16 Гц. Таким образом, L= 15,5 Гц. Че­редующиеся нисходящие и восходящие ряды повторяются возможно боль­шее число раз или до тех пор, пока экспериментатор не убедится в относи­тельном единообразии величины L. В последующих рядах он изменяет начальную точку, чтобы у испытуемого не формировались ложные пред­ставления. Трудно оценить околопороговые стимулы и даже добросовест­ный испытуемый может впасть в ошибку, руководствуясь каким-нибудь побочным признаком, который по его мнению облегчает выполнение за­дания.

Вычисление абсолютного порога по этим данным проводится следу­ющим образом: величины RLмогут быть усреднены (среднее арифметичес­кое) тремя способами (два из них указаны внизу таблицы): 1) все отдель­ные величины L, указанные под верхней линией, суммируются и усред­няются. Среднее значение — 14,5 Гц принимается за абсолютный порог. Среднее квадратичное отклонение этого распределения отражает вариа­бельность работы наблюдателя; 2) под второй линией приведены результа­ты усреднения каждой пары величин L, (одна из нисходящего, другая из следующего восходящего ряда). Эти усреднения делаются для того, чтобы получить средние в паре рядов значения L - Уср. L. Затем вычисляется среднее из этих средних. Значение абсолютного порога остается, разумеет­ся, тем же, но среднее квадратичное отклонение будет меньше за счет ис­ключения вариабельности, связанной с отдельными нисходящими и восхо­дящими рядами; 3) все величины Lв нисходящих рядах можно усреднить, чтобы получить значение абсолютного порога в нисходящем ряду². Таким же образом усредняются все величины Lв восходящих рядах. Окончатель­ное значение абсолютного порога является средним арифметическим этих двух средних. Само собой разумеется, что его численное значение будет таким же, как и в двух предыдущих способах, хотя значения порогов в восходящих и нисходящих рядах могут быть разными из-за определенных «постоянных ошибок». Ошибкой привыкания является тенденция сохра­нять ответ «да» в нисходящих рядах или ответ «нет» в восходящих рядах. Ошибка предвосхищения (или ожидания) имеет противоположный харак­тер. Она связана с ожиданием перемены и, таким образом, сменой ответа «да» на ответ «нет» в нисходящем ряду и «нет» на «да» — в восходящем.

¹ L— от лат. Limen— порог. (Примечание редактора источника.)

² В отечественной литературе этот порог называется порогом исчезновения, а такой
же порог в восходящем ряду — порогом появления ощущения. (Примечание редактора
источника.)

Энген Т. Основные методы психофизики

15

Основная цель чередования нисходящих и восходящих рядов — сбаланси­ровать любую из постоянных ошибок, если они возникают. Совпадение значений на шкале стимулов в восходящих и нисходящих рядах указыва­ет на привыкание, а их расхождение — на предвосхищение (ожидание). Опыт и утомление оказывают противоположные влияния на результаты эксперимента, их легко оценить, сравнивая первую и вторую половины общего количества предъявленных рядов. Более точно эти влияния мож­но изучить при помощи анализа вариабельности¹. Оценкой достоверности абсолютного порога может служить стандартная ошибка среднего, вычис­ляемая по обычной формуле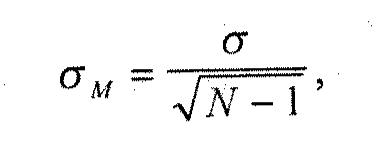




где — среднее квадратичное отклонение (стандартное отклонение) рас­пределения значений L, а N — количество восходящих и нисходящих рядов. Что касается задачи испытуемого при определении абсолютного порога методом границ, то желательно, чтобы он ограничивался двумя категориями ответов, «да» и «нет», и пытался угадывать, когда он не уве­рен. Это делается для того, чтобы избежать ответа «сомнительно», внезап­но появившегося в данных Титченера, приведенных в табл. 1. Это осо­бенно важно отметить потому, что в современной психофизике нередко используются малотренированные испытуемые.

Разностный порог

В целом процедура измерения разностного порога такая же, как и абсолютного, но чаще используются три, а не две категории ответов. Ги­потетические данные приведены в табл. 2. Для сравнения в каждой пробе предъявляются два стимула: переменный и стандартный. Для оценки пе­ременного стимула по отношению к стандартному предписывается исполь­зовать три категории ответов, соответствующих исследуемой модальности, например, такие как «больше» (+), «меньше» (-) и «равны» (=). Инструк­ция обязывает испытуемого угадывать категорию ответа, когда он не мо­жет уверенно различать стимулы. В этом случае для определения значений Lрекомендуется следующая процедура: в нисходящем ряду надо учиты­вать только первый переход от «плюса» к «равно» и первый переход от «равно» к «минусу». Точно так же в восходящем ряду учитывается первый переход от «минуса» к «равно» и от «равно» к «плюсу».

Экспериментатор начинает, как и в предыдущем примере, со сти­мула, значительно превышающего стандартный, и идет по нисходящему ряду. Когда сравнительный стимул становится равен 5, положительная оценка испытуемого сменяется на оценку «равно». Экспериментатор про-

¹ См.: Gullford J.P. Psychometric methods. N.Y.: McGraw-Hill, 1954.

16

Тема 17. Экспериментальные исследования восприятия

должает нисходящий ряд и первая оценка «минус» появляется на зна­чении стимула, равном 3. Если разделить пополам шаговые интервалы¹, с которыми совпадает переход к другой категории ответа, то можно по­лучить значения Lдля этого ряда: L(+) = 5,5 и L (-) = 3,5. Подсчеты в других столбцах показывают, как следует применять это правило в дру­гих рядах.

Для вычисления среднего по таблице в целом необходимо опреде­лить средние значения L(+) и L(-). Таким образом, весь диапазон срав­ниваемых стимулов будет разделен на две части: в верхней части преоб­ладают положительные оценки, в нижней — отрицательные, а в средней остается интервал неопределенности (ИН), где чаще всего встречаются оценки «равно». Интервал неопределенности охватывает зону величиной в два разностных порога или е. з. р.: от «минуса» до «равно» и от «рав­но» до «плюса». А разностный порог, измеренный этим методом, опре­деляется как ИН/2, т.е. 1,25/2 = 0,625. Это та физическая величина, добавление которой к стандартному стимулу (или уменьшение стандар­та на эту величину) испытуемый всегда замечал бы, если бы не было константной ошибки. Средняя точка интервала неопределенности (равная




= 4,5) принимается за наиболее точную

¹ Интервал изменения переменного стимула. (Примечание редактора источника.)

Энген Т. Основные методы психофизики

17

оценку точки субъективного равенства (TCP). Теоретически это та точ­ка, где с наибольшей вероятностью переменный стимул кажется равным стандартному или где число оценок «плюс» и «минус» одинаково. Как ни странно, точка субъективного равенства редко совпадает со стандар­том. Если она расположена выше стандарта, то имеет место так называ­емая положительная константная ошибка (КО), если ниже стандарта, то отрицательная ошибка, как в последнем примере, где стандарт равен 5, а точка субъективного равенства — 4,5. Следует отметить, что эти константные ошибки уравновешиваются при вычислении разностного порога; иногда при исследовании восприятия они представляют интерес сами по себе.

Закон Вебера

Физический стимул, соответствующий разностному порогу, называют

Часто представляет интерес относительный порог различения, определяемый как S/S или отношение наименьшего замечаемого разли­чия к интенсивности стимула. В нашем примере S/S= 0,625/4,5. Эта дробь получила название дроби Вебера. Согласно закону Вебера, она дол­жна быть постоянной для различных значений раздражителя:

S/S= k, S= kS.

S/Sразлична для разных сенсорных модальностей, но постоянна для данной модальности при умеренных значениях стимула. Однако она существенно возрастает, когда S(величина стимула) приближается к порогу раздражения (абсолютному порогу). Отметим, что при вычисле­нии дроби Вебера чаще используется точка субъективного равенства, чем стандарт, так как обычно оценки распределяются более симметрично относительно этой точки, а не стандарта. При вычислении дроби Вебера для практического использования это несущественно. Согласно закону Вебера, по мере уменьшения стимула Sдолжно уменьшиться и Sи, следовательно, на абсолютном пороге Sдолжно быть наименьшим. Од­нако данные, приведенные на рис. 1, показывают, что этого не происхо­дит: на самом деле Sувеличивается при приближении к абсолютному порогу. Психофизики послефехнеровской поры¹ сознавали эту неадекват­ность закона Вебера и связывали ее с проблемой абсолютного порога. Поэтому был предложен модифицированный вариант закона Вебера, со­гласно которому

S/S + а= k или S = k(S + a),

где а — очень малая величина в континууме стимулов, близкая к абсо­лютному порогу, но не равная ему. Прибавление а к SделаетS/S + a

¹ См.: Stevens S.S. (Ed.) Handbook of experimental psychology, N.Y.; Wiley, 1951. С. 36.