тест по статистике. Гладун И. В_Статистика СКАН. Учебника для использования в учебном процессе образовательных учреждений, реализующих программы спо

• Название: Учебника для использования в учебном процессе образовательных учреждений, реализующих программы спо
• Анкор: тест по статистике
• Дата: 27.09.2022
• Размер: 1.13 Mb.
• Имя файла: Гладун И. В_Статистика СКАН.docx
• Тип: Учебник; #699128
• страница: 44 из 50

Характеристика корреляционного анализа

Статистическая категория	Содержание категории
Парная корре- ляция	Это связь между двумяколичественными переменными
Множествен- ная корреляция	Это связь между результативным показателем (Y) и не- сколькими признаками-факторами (Х1, Х2, …, Хn)
Частная корре- ляция	Это зависимость между результативнымпоказателем (Y) и одним признаком-фактором (Х1), при устранении влия- ния другого фактора (Х2)
Парный коэф- фициент корре- ляции	Характеризует тесноту и направление связи между двумя количественными переменными
Линейный коэффициент корреляции r	Характеризует тесноту и направление связи между двумя признаками в случае наличия между ними линейнойзави- симости
Множествен- ный коэффи- циент корреля- ции R	Вычисляется при наличии линейной связи между резуль- тативным (Y) и несколькими факторными (Х1, Х2, …, Хn) признаками, а также между каждой парой факторных при- знаков (Х1, Х2). 0  R  1
Частные ко- эффициенты корреляции r	Характеризуют степень тесноты связи между двумя при- знаками Х1 и Х2 при фиксированномзначении других фак- торных признаков

В таблице 10.5 представлены значения линейного коэффициента, поясняется их смысл.

10.2. регрессионно-корреляционный анализ_•199

Таблица 10.5

Линейный коэффициент корреляции и его характеристика

Значение ли- нейного коэф- фициента связи	Характеристика связи	Пояснения
r= 0	Отсутствует	—
0 < r< 1	Прямая	С увеличением Хувеличивается Yи на- оборот
–1 < r< 0	Обратная	С увеличением Хуменьшается Yи на- оборот
r= 1	Функциональная	Каждому значению Хстрого соответ- ствует одно значение Y

Характеристика величины коэффициента корреляции дана в табл. 10.6.

Таблица 10.6

Количественные критерии оценки тесноты связи

Величина коэффициента корреляции	Сила связи
До ±0,3	Практически отсутствует
От ±0,3 до ±0,5	Слабая
От ±0,5 до ±0,7	Умеренная
От ±0,7 до ±1,0	Сильная

В таблице 10.7 представлено содержание основных категорий ре- грессионного анализа.

Таблица 10.7

Характеристика регрессии

Статистическая категория	Содержание категории
Регрессия	Это зависимость среднегозначения случайной величины Y от других величин Х1, Х2, …, Хn
Парная регрес- сия	Это форма связи между двумяпризнаками (Y, Х1)
Многофактор- ная регрессия	Это изучение связи между тремяи более связанными между собой признаками (Y, Х1, Х2, …, Хn)
Парная линей- ная регрессия	Yx= a0 + a1x
Множествен- ная линейная регрессия	Yx= a0 + a1x1 + a2x2 +… + anxn

200_•глава 10. статистические метОды изучения взаимОсвязей...

Окончание

Статистическая категория	Содержание категории
Параболиче- ская регрессия	Yx= a0 + a1x+ a2x2
Показательная регрессия	Yx aax 0 1
Гиперболиче- ская регрессия	Y a a1 x0 1 x

В таблице 10.8 дается характеристика коэффициентам (параме- трам) уравнения регрессии.

Таблица 10.8

Характеристика коэффициентов регрессии

Статистическая категория	Содержание категории
Величина ко- эффициента регрессии ai	Чем больше величина коэффициента регрессии, тем зна- чительнее влияние факторного признака на результатив- ный признак
Знак коэффи- циента регрес- сии «+» или «–»	Знак плюссвидетельствует о прямойсвязи между Xи Y, т.е. с увеличением фактора Х результативный признак Y воз- растает. Знак минуссвидетельствует об обратной связи: с увеличе- нием Хуменьшается Y

Коэффициенты (параметры) уравнения регрессии показывают:

a0	Усредненное влияние на результативный признак (Y) не- учтенных в уравнении факторных признаков (Х)
a1	На сколько в среднем изменяется значение Y при измене- нии Х1 на единицу собственного измерения
a2	На сколько единиц изменится Y, если Х2 изменится на единицу
an	На сколько единиц изменится Y, если Хnизменится на единицу

Кроме парной регрессии рассмотрим множественную регрессию. Число факторов, включаемых в модель множественной зависимо-

сти, должно быть в 5—6 раз меньше числа единиц, входящих в сово- купность.

Линейное уравнение множественной зависимости Yот Х₁, Х₂, …, Х_n:

^yx₁x₂ ...x_n

 a₀  a₁x₁  a₂ x₂  ...  a_nx_n.

10.2. регрессионно-корреляционный анализ_•201

Линейное уравнение множественной зависимости Yот Х₁, Х₂:


1 2
y_xx a₀  a₁x₁  a₂ x₂.

Система нормальных уравнений:

^na₀  a_{1 } x₁  a_{2 } x₂  _ y

^ax ax²  axx yx.

^ 0  1 1  1 2  2 1  1

^ax axx ax²  yx

_ 0  2 1  1 2 2  2  2

Коэффициент множественной (совокупной) корреляции приме- няется для измерения тесноты связи между изменениями величины результативного признака Y и изменениями значений факторных при- знаков Х₁, Х₂:

r²  r²  r r

.
^Ryx₁x₂ ^

yx₁yx₂yx₁yx₂


1 r
2

x₁x₂

Если число факторов-признаков более двух, то совокупный коэф- фициент корреляции (детерминации) определяется по формуле

R
2

yx₁x₂ ...x_n

 1  ^,



где ^R
2

yx₁x₂ ...x_n

• 
  коэффициент детерминации;
  

 — матрица парных коэффициентов корреляции;

'' — матрица парных коэффициентов корреляции () без верх- ней строки и первого столбца.

0  R
2

yx₁x₂ ...x_n

 1.

Чем ближе коэффициент детерминации к единице, тем меньше роль неучтенных факторов в модели, тем более оснований считать, что параметры регрессионной модели отражают степень эффективности включенных в нее факторов.

Частныекоэффициентыкорреляциидополняют совокупный и по- зволяют установить степень тесноты связи между результативным признаком и каждым из факторных признаков при исключении ис- кажающего влияния других факторных признаков.

Коэффициенты частной корреляции отражают степень чистого влияния факторного признака на результативный признак.

Если рассматривается зависимость результативного признака от двух факторных, то определяется два коэффициента частной кор- реляции:

202_•глава 10. статистические метОды изучения взаимОсвязей...

1. 
   между результативным признаком и признаком-фактором X₁
   

при элиминировании фактора X₂:

^ryx^{ r}yx^{ r}xx

_{ryx( x) } 12 12 _;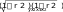

2. 
   между результативным признаком и признаком-фактором X₂
   

при элиминировании фактора X₁:

^ryx^{ r}yx^{ r}xx


2 1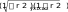


_{ryx( x) } 2 1 1 2 _.

Коэффициенты частной корреляции находятся в пределах от нуля до единицы (по модулю).

Чтобы сравнить роль различных факторов в формировании моде- лируемого показателя, исчисляются коэффициент эластичности (Э_j) или -коэффициент (_j):




Э  a^xj,

j j_y

где a_j— коэффициент регрессии при j-м факторе.

Частный коэффициент эластичности показывает, на сколько про- центов в среднем изменяется результативный признак Yс изменением признака-фактора Х на 1%.

 _x

  a^j.

j j_

y

-коэффициент показывает, на какую часть среднего квадратиче- ского отклонения изменится результативный признак Y при измене- нии соответствующего признака-фактора Х на величину его среднего квадратического отклонения.

Рассмотрим методику регрессионно-корреляционного анализа на примере решения задачи 10.1.

Задача 10.1. Имеются следующие данные об экзаменационных оцен- ках и количестве часов пропущенных учебных занятий студентами кол- леджа группы № 22 по дисциплине «Экономика организации» (табл. 10.9):

Таблица 10.9

№ п/п	1	2	3	4	5	6	7	8	9	10
Экзаменационная оценка	4	3	5	4	2	3	5	3	4	3
Количество пропущенных занятий, ч	2	4	2	3	3	4	2	3	1	4

10.2. регрессионно-корреляционный анализ_•203

По данным табл. 10.9 необходимо провести РКА взаимосвязи меж- ду успеваемостью и посещаемостью студентов колледжа.

Определим уравнение линейной регрессии между двумя признака- ми — экзаменационной оценкой (Y) и количеством пропусков учеб- ных занятий (Х).

Решение.

1. 
   На основании предварительного теоретического анализа пред- положим наличие обратной стохастической связи между успевае- мостью (Y — результативный признак) и посещаемостью учебных занятий (Х — признак-фактор), что с увеличением количества пропу- щенных учебных занятий успеваемость студентов снижается.
   

Показателем успеваемости (Y) будет экзаменационная оценка, полученная студентами по дисциплине «Экономика организации» по итогам зимней сессии. Показателем посещаемости (Х) — количе- ство часов учебных занятий, пропущенных студентами группы по дис- циплине «Экономика организации» за семестр.

2. 
   Проверим однородность первичных данных по признаку-фак- тору Х, для чего рассчитаем коэффициент вариации V_x, представив расчеты в табл. 10.10.
   

Таблица 10.10

№	x	x x	(x x)2	№	x	x x	(x x)2
1	2	–0,8	0,64	6	3	+0,2	0,04
2	4	+1,2	1,44	7	2	–0,8	0,64
3	2	–0,8	0,64	8	3	+0,2	0,04
4	3	+0,2	0,04	9	1	–1,8	3,24
5	4	+1,2	1,44	10	4	+1,2	1,44
Х	Х	Х	Х	Итого:	28	Х	9,60

V ^x 100%; x_x

i

x ^x ²⁸  2,8 ч;

n10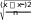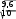

 _x  

0,98 ч;

x
V ^x100%  ^0,98100%  35%  33%.

x_i2,8

204_•глава 10. статистические метОды изучения взаимОсвязей...