тест по статистике. Гладун И. В_Статистика СКАН. Учебника для использования в учебном процессе образовательных учреждений, реализующих программы спо

• Название: Учебника для использования в учебном процессе образовательных учреждений, реализующих программы спо
• Анкор: тест по статистике
• Дата: 27.09.2022
• Размер: 1.13 Mb.
• Имя файла: Гладун И. В_Статистика СКАН.docx
• Тип: Учебник; #699128
• страница: 45 из 50

Вывод. Исчисленный коэффициент вариации (35%) больше 33%, что свидетельствует о неоднородности совокупности по признаку- фактору Х. Однако для продолжения дальнейшего исследования до- пустим, что совокупность однородна.

3. 
   Проверим (с помощью правила «трех сигм») распределение пер- вичных данных на соответствие нормальному распределению. Расче- ты представлены в табл. 10.11.
   

Таблица 10.11

Интервалы значений признака x x  2,8 x= 0,98	Интерва- лы значе- ний при- знака x, ч	Количество единиц, входящих в интервал	Удельный вес единиц, входя- щих в интер- вал, в общем их числе, %	Удельный вес единиц, входящих в интервал, при нормальном рас- пределении, %
xix	1,8—3,8	9	90	68,3
xi 2 x	0,8—4,8	10	100	95,4

Вывод. Распределение первичных данных (Х) подчиняется закону нормального распределения.

Следует отметить, что на практике РКА применяют даже в тех слу- чаях, когда нарушаются требования нормальности распределения и однородности совокупности.

4. 
   Исключим из массива первичных данных аномальные единицы, т.е. единицы, которые не попадают в интервал ^{xi  3 x xi  xi  3 x.}
   

Вывод. Таких единиц нет (см. табл. 10.11).

5. 
   Проверим наличие связи между Х и Y методом аналитической группировки. Расчеты представлены в табл. 10.12.
   

Таблица 10.12

Количе- ство про- пусков x, ч	Количество студентов ni, человек	Сумма бал- лов  yi	Средний балл yi	yi y0	( yi y0 )2 ni
1	1	4	4,0	+0,4	0,16
2	3	14	4,7	+1,1	3,63
3	3	10	3,3	–0,3	0,27
4	3	8	2,7	–0,9	2,43
Итого:	10	36	3,6 = y0	Х	6,49

Вывод. Результаты аналитической группировки подтверждают тео- ретическое предположение о наличии обратной стохастической связи между факторами Хи Y: с увеличением количества часов пропусков

учебных занятий (Х) средний балл (^Y) уменьшается.

10.2. регрессионно-корреляционный анализ_•205

6. 
   Если данные Х и Y нанести на график, то эмпирическая линия связи по своей форме приближается к прямой линии. Следовательно, можно принять наличие прямолинейной корреляционной связи меж- ду Х и Y и в дальнейшем рассчитать параметры линейного уравнения регрессии.
   
7. 
   Измерим тесноту корреляционной связи между Хи Yс помощью линейного коэффициента корреляции (r). В таблице 10.13 произведем необходимые вычисления.
   

Таблица 10.13

Расчет коэффициента корреляции и параметров уравнения линейной регрессии

№	Y	Х	Х2	ХY	Y2	y y	( y y)2	yˆ	y yˆ	(y yˆ)2
А	1	2	3	4	6	7	8	9	10	11
1	4	2	4	8	16	+0,4	0,16	4,17	–0,17	0,0289
2	3	4	16	12	9	–0,6	0,36	2,75	+0,25	0,0625
3	5	2	4	10	25	+1,4	1,96	4,17	+0,83	0,6889
4	4	3	9	12	16	+0,4	0,16	3,46	+0,54	0,2916
5	2	4	16	8	4	–1,6	2,56	2,75	–0,75	0,5625
6	3	3	9	9	9	–0,6	0,36	3,46	–0,46	0,2116
7	5	2	4	10	25	+1,4	1,96	4,17	+0,83	0,6889
8	3	3	9	9	9	–0,6	0,36	3,46	–0,46	0,2116
9	4	1	1	4	16	+0,4	0,16	4,88	–0,88	0,7744
10	3	4	16	12	9	–0,6	0,36	2,75	+0,25	0,0625
Итого:	36	28	88	94	138	Х	8,40	Х	Х	3,5834

_ xy ^xy

_{94 } 2836

r  ⁿ ¹⁰  0,757.

 ₂₈²  

36^{2 }

_88  _{10  }138  _{10 }
Вывод. Отрицательный знак исчисленного коэффициента кор- реляции (–0,757) свидетельствует о наличии обратной связи между факторами Хи Y. Связь сильная, так как величина коэффициен- та корреляции (по модулю) находится в интервале от 0,7 до 1,0 (см. табл. 10.6).

8. 
   Проверим существенность исчисленного линейного коэффи- циента корреляции, для чего рассчитаем среднюю квадратическую ошибку (_r) и значение t-критерия (t_расч), сравнив последнее с таблич- ным значением t-критерия Стьюдента:
   

206_•глава 10. статистические метОды изучения взаимОсвязей...

_r 

1  0,757² _

10  2
0,231;


^tрасч ^

r

 ^0,757  3,277.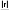

0,231

Табличное значение t-критерия Стьюдента равно 2,306. Оно опре- делялось по таблицам для распределения Стьюдента при числе степе- ней свободы k= n– 2 = 10 – 2 = 8 и с вероятностью Р= 0,95 (уровне значимости  = 0,05).

Вывод. Расчетное значение t-критерия (3,277) больше табличного (2,306), что свидетельствует о существенности линейного коэффици- ента корреляции.

9. 
   Рассчитаем параметры линейного уравнения регрессии (мето- дом наименьших квадратов):
   

Y_x a₀  a₁x;

^_na₀  a_{1 } x _ y

^a x ax²  yx<sup>;

</sup>_ 0  1  


^28a₀  88a 94₁
^{10a0  28a1  36}_;



_a ^xynxy_ ^{94102,83,6}_{ 0,71;}

¹ _ x²  nx² 88 10  2,8²

a₀  y a₁x 3,6  0,71 2,8  5,59;




Y_x 5,59  0,71x.

Вывод. При увеличении количества пропусков учебных занятий на 1 ч экзаменационная оценка снижается на 0,71 балла.

10. 
    Проверим возможность использования линейной функции, для чего рассчитаем ² и сравним с табличным значением F-критерия. Если ² будет меньше табличного значения F-критерия, то гипотеза о возможности использования в качестве уравнения регрессии линей- ной функции не опровергается.
    

_{2 } ²  r² _ 1  ²

m 2 n m^;

²  ^2



₂ ;

y

2. 
   регрессионно-корреляционный анализ_•207
   

_( y_i y₀ )² n_i
6,49

²    0,649;

_n_i¹⁰


 i^8,40
( y y)²

²    0,840;

^yn10

_{2 } ² _ 0,649 _



0,7726;


y
² 0,84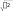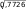

    0,879;

_{2 } ²  r² _ 1  ² _ 0,7726  0,757² _ 10,7726 _

2,633.

m 2

n m

4  2

10  4

По таблице значений F для доверительной вероятности Р= (1 –

– ) = 0,95 и степеней свободы k₁ = m– 2 = 4 – 2 = 2 и k₂ = n– m=

= 10 – 4 = 6 F-табличное составляет 5,14, что превышает исчисленный показатель ² = 2,633.

Вывод. Гипотеза о возможности использования в качестве уравне- ния регрессии линейной функции не опровергается.

11. 
    Проверим достоверность уравнения регрессии, т.е. оценим сте- пень точности отражения взаимосвязи между Xи Y, для чего рассчита- ем следующие показатели:
    

^Se100%;

y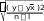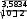
S_e   0,669,

где S_e— средняя квадратическая ошибка уравнения регрессии;

^y— средний уровень результативного признака;

y— фактические значения результативного признака;

^yx— значения результативного признака, рассчитанные по урав- нению регрессии ^{yx  5,59  0,71x;}

n— количество единиц наблюдения;

l— число параметров в уравнении регрессии.

^Se100%  ^0,669 100%  18,6%.

y3,6

Вывод. Отношение ^Se100% превышает 10—15%, следовательно,

y

уравнение регрессии недостаточно хорошо отображает изучаемую сто-

208_•глава 10. статистические метОды изучения взаимОсвязей...

хастическую взаимосвязь между экзаменационной оценкой Y и коли- чеством пропусков учебных занятий X.

Следует заметить, что небольшой объем совокупности, взятый для анализа (десять наблюдений), не смог обеспечить достаточную достоверность и надежность результатов РКА. Необходимо исполь- зовать значительно больший массив первичных данных. Только в этом случае регрессионная модель будет иметь практическое зна- чение для проведения глубокого анализа финансово-хозяйствен- ной деятельности предприятия, выявления неиспользованных ре- зервов, принятия обоснованных и эффективных управленческих решений.

В настоящее время для обработки экономической информации широко используются возможности компьютерной техники. Специ- ально разработанные программы позволяют значительно облегчить труд экономиста, ускорить процесс расчетов, что позволяет прини- мать оперативные управленческие решения.

2. 
   Задания для самостоятельной работы
   

Овладев знаниями, еще больше продви- нешься в действии.

СуньЯт-сен

Задание_10.1.'>Задание 10.1. Приведите примеры функциональной и стохастиче- ской зависимости. По каждому примеру укажите факторный и резуль- тативный признаки, охарактеризуйте форму связи между ними.

Задание 10.2. Оцените тесноту связи между результативным при- знаком Y и признаками-факторами x₁, x₂, x₃, x₄, если парные коэф- фициенты корреляции соответственно равны 0,911; 0,903; 0,249;

0,979.

Y— годовая производительность труда рабочего, тыс. руб./человек;

x₁ — вооруженность труда основными производственными фонда- ми, тыс. руб./человек;

x₂ — удельный вес оборудования в стоимости основных фондов, %;

x₃ — текучесть кадров, %;

x₄ — интегральный показатель использования рабочего времени, в долях единицы.

Дайте интерпретацию параметрам уравнения регрессии:

Y= 48,27 + 4,43x₁ + 253,63x₄.

10.3. задания для самостоятельной работы_•209

Задание 10.3. Дайте интерпретацию параметрам уравнения ре- грессии:

Y= –56,5 + 0,38x₁ + 0,67x₂,

где Y— цена бумаги, руб.;

x₁ — плотность бумаги, г/м²;

x₂ — белизна, %.

Задание 10.4. Используя материалы периодической печати, интер- нет-ресурсы, подберите примеры использования корреляционно-ре- грессионного метода для изучения социально-экономической жизни общества, в управлении предприятием. Приложите вырезки из газет, журналов, распечатки интернет-сайтов.

Задание 10.5. Дайте ответы на вопросы теста.

1. 
   Между квалификацией рабочего и заработной платой существу- ет связь:
   

а) функциональная; б) стохастическая;

в) связи не существует.

2. 
   Квалификация рабочего относительно заработной платы — это: а) признак-фактор;
   

б) результативный признак; в) зависимости не существует.

3. 
   Между квалификацией рабочего и заработной платой связь: а) прямая;
   

б) обратная;

в) нельзя определить направление связи.

4. 
   Установите соответствие между значением линейного коэффи- циента связи и характером связи:
   

Характеристика связи	Значение линейного коэффициента связи
1. Функциональная	А) r= 0
2. Обратная	B) 0 < r< 1
3. Прямая	C) –1 < r< 0
4. Отсутствует	D) r= 1
	E) –1 < r< 1

а) 1 — A, 2 — C, 3 — B, 4 — D;

б) 1 — D, 2 — C, 3 — В, 4 — A;

в) 1 — E, 2 — C, 3 — A, 4 — B;

г) 1 — D, 2 — E, 3 — B, 4 — C.

210_•глава 10. статистические метОды изучения взаимОсвязей...

5. 
   Укажите правильную последовательность этапов регрессионно- корреляционного анализа:
   
   1. 
      сбор информации, ее первичная обработка;
      
   2. 
      предварительный (априорный) анализ;
      
   3. 
      оценка и анализ модели;
      
   4. 
      построение модели (уравнения) регрессии. а) 1—2—4—3;
      

б) 1—2—3—4;

в) 2—1—4—3;

г) 2—1—3—4.

6. 
   Если коэффициент корреляции находится в пределах от ±0,7 до ±1,0, следовательно, связь:
   

а) практически отсутствует; б) слабая;

в) умеренная; г) сильная.

7. 
   Установите соответствие между методом выявления стохастиче- ской связи и его содержанием:
   

Метод выявле- ния стохасти- ческой связи	Содержание метода
1. Метод парал- лельных рядов	A) Определение формы связи, т.е. ее аналитического вы- ражения (формулы)
2. Аналитиче- ская группи- ровка	B) Значения Х и Y изображают на графике в форме корре- ляционного поля, по форме которого определяют наличие или отсутствие связи и ее форму
3. Корреляци- онный анализ	C) Производят группировку единиц совокупности по при- знаку-фактору. Для каждой группы исчисляют среднее значение результативного показателя
4. Регрессион- ный анализ	D) Определение тесноты и направления связи между при- знаками
	E) Сопоставление ранжированных рядов статистических показателей, отражающих значения признака-фактора и результативного показателя

а) 1 — E, 2 — C, 3 — B, 4 — D;

б) 1 — B, 2 — C, 3 — E, 4 — A;

в) 1 — E, 2 — C, 3 — D, 4 — A;

г) 1 — D, 2 — E, 3 — A, 4 — C.

Ответы: 1 — б; 2 — а; 3 — а; 4 — б; 5 — в; 6 — г; 7 — в.

глава11

ВыБОРОчНОЕ НАБЛюДЕНИЕ
Мы живем в вероятностном мире и в боль- шинстве принимаемых нами решений содер- жится элемент риска.

Кимбал