тест по статистике. Гладун И. В_Статистика СКАН. Учебника для использования в учебном процессе образовательных учреждений, реализующих программы спо

• Название: Учебника для использования в учебном процессе образовательных учреждений, реализующих программы спо
• Анкор: тест по статистике
• Дата: 27.09.2022
• Размер: 1.13 Mb.
• Имя файла: Гладун И. В_Статистика СКАН.docx
• Тип: Учебник; #699128
• страница: 47 из 50

Ошибки выборки

Ошибка выборки (систематическая, случайная) — это отклонение величины изучаемого признака в выборке от величины данного при- знака во всей генеральной совокупности: ^{ x  x}или ^{w p.}

Систематическая ошибка выборки (преднамеренная, непреднаме- ренная) возникает вследствие нарушения правил беспристрастного, случайного отбора. Она не поддается количественной оценке.

Случайная ошибка выборки возникает при проведении любого вы- борочного наблюдения в силу его несплошного характера.

Величина случайной ошибки выборки зависит:

1. 
   от объема выборки (чем больше объем, тем меньше ошибка);
   
2. 
   степени колеблемости изучаемого признака в генеральной сово- купности (чем больше степень колеблемости, тем больше ошиб- ка репрезентативности);
   
3. 
   способа формирования выборочной совокупности (например, ошибка серийной выборки больше, чем ошибка при другом спо- собе отбора).
   

Если выборка проведена по всем правилам, то ошибка выборочно- го наблюдения может быть меньше ошибки сплошного наблюдения (за счет значительного уменьшения величины ошибки регистрации).

Исчисление случайной ошибки репрезентативности основывается на теории вероятности (теоремы П.Л. Чебышева, А.М. Ляпунова). До- казано, что при достаточно большом числе независимых наблюдений в генеральной совокупности с конечной средней величиной и ограни-

ченной дисперсией вероятность того, что расхождение между выбо- рочной и генеральной средней ( ^{x  x} ) не превзойдет по абсолютной величине некоторую величину t, равна интегралу Лапласа:

218_•глава 11. выбОрОчнОе наблюдение


2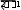
₁ 1 t

(t) 

_ e² dt;

^P ^{x  x t} ^{ (t),}

где (t) — интеграл Лапласа (нормированная функция Лапласа явля- ется функцией от t);

t — коэффициент кратности средней ошибки выборки, зави- сящей от вероятности, с которой гарантируется величина предельной ошибки;

 — средняя ошибка выборки;

Р — принятая доверительная вероятность того, что ошибка вы- борки на превысит заданную величину ;

t =  — предельная ошибка выборки;

^{x  x } — доверительные пределы генеральной средней;

^{w p } — доверительные пределы генеральной доли.

В зависимости от принятой вероятности Р определяется значение коэффициента кратности (t) по удвоенной нормированной функции Лапласа.

Величина случайной ошибки определяет надежность данных выбо- рочного наблюдения.

Различают среднюю и предельную ошибки выборки.

Если несколько раз провести выборку единиц из одной и той же со- вокупности, то ошибки репрезентативности будут по величине разные

₁  ₂ …  _n, но в среднем ошибка будет равна .

На практике выборку проводят только один раз. Величина ошибки данной выборки ₁ будет отличаться от средней ошибки (₁ < ; ₁ > ;

₁ = ). Поэтому надо знать пределы, в которых может находиться ошибка выборки ₁.

Эти пределы зависят от вероятности, с которой можно гарантиро- вать, что ошибка ₁ не превысит заданную величину. Такая ошибка на- зывается предельной.

Предельная (максимально возможная) ошибка выборки () — это та- кая величина отклонения выборочной средней (или доли) от генераль- ной, вероятность превышения которой вследствие случайных причин в условиях данной выборки очень мала:

 _x t_x;

 _p t _p,

где ^{ x}— предельная (максимально возможная) ошибка средней ве- личины;

2. 
   Ошибки выборки_•219
   

_p— предельная (максимально возможная) ошибка доли;

^x— средняя ошибка средней величины;

_p— средняя ошибка доли.

Методика расчета средней и предельной ошибок собственно-слу- чайной выборки представлена в табл. 11.3.

Таблица 11.3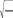

Формулы ошибок собственно-случайной выборки

Вид ошибки выборки	Методы отбора единиц
	повторный	бесповторный
Средняя ошибка для средней, x	2 n	2  n n1 N
Средняя ошибка для доли, p	w(1w) n	w(1w) 1 n n N
Предельная ошибка для средней,  x	2 t n	2  n t 1  n N
Предельная ошибка для доли, p	t w(1w) n	t w(1w) 1 n n N

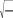На практике показатели генеральной совокупности (дисперсия, доля) неизвестны. В расчетах их значения заменяют показателями, ис- численными по выборочным данным (² и w), которые получены либо в предшествующих обследованиях, либо в пробных выборках. По- грешность в данном случае увеличивается.

Если n очень мало по сравнению с N (меньше 5%), то ошибка бес- повторного отбора практически не отличается от ошибки повторного. Чем ближе n к N, тем больше они различаются.

Когда численность генеральной совокупности N неизвестна, при- меняют формулы ошибки случайного повторного отбора, тем самым несколько преувеличивая запас надежности.

Исчисление ошибок выборки при проведении механического, ти- пического и других отборов основывается на формулах расчета оши- бок собственно-случайного отбора.

Ошибка выборки при механическом отборе находится между ошибкой случайного повторного и бесповторного отбора. Ошибка при бесповторном отборе меньше ошибки повторного отбора.

При проведении механической выборки применяют формулы соб- ственно-случайной повторной выборки.

220_•глава 11. выбОрОчнОе наблюдение

При типическом отборе вместо общей дисперсии ² используют среднюю из групповых дисперсий ^2. Чем сильнее группы отличают- ся друг от друга, тем меньше ошибка выборки.

При серийном(групповом) отборе вместо общей дисперсии ² ис-

пользуют межгрупповую дисперсию ², вместо отобранных единиц

(n) — количество отобранных серий.