тест по статистике. Гладун И. В_Статистика СКАН. Учебника для использования в учебном процессе образовательных учреждений, реализующих программы спо

• Название: Учебника для использования в учебном процессе образовательных учреждений, реализующих программы спо
• Анкор: тест по статистике
• Дата: 27.09.2022
• Размер: 1.13 Mb.
• Имя файла: Гладун И. В_Статистика СКАН.docx
• Тип: Учебник; #699128
• страница: 48 из 50

Определение показателей выборки

В процессе выборочного наблюдения в зависимости от того, про- ведена выборка или только планируется, от требуемой точности обоб- щающих характеристик решаются задачи трех типов.

Тип 1. Определить пределы генеральных характеристик ( ^{ x,} _p)

с заданной степенью надежности (доверительной вероятностью) (P_t) на основе показателей, полученных по данным выборки (табл. 11.4).

Заданы или известны величины: n, ², ^x, P(t).
Таблица 11.4

Показатели	Для генеральной средней	Для генеральной доли
Доверительные интервалы	x x  x	p w  p
	x  x x x  x	w p x w p
Предельная ошибка	 x tx	 p t p

Тип 2. Определить доверительную вероятность Р(t) того, что гене- ральная характеристика ( ^xили p) может отличаться от выборочной

( ^x

или w) не более чем на определенную заданную величину (). Заданы или известны величины: n, N, ^x, , ², ^{ x,} w, _p.

Доверительная вероятность (Р) является функцией от t:

t ^x;

_x

t ^p .

 _p

Величина доверительной вероятности (Р) зависит от t и определя- ется по таблицам, где

при t= 1, P= (  ) = (1) = 0,683;

при t = 2, P = (  2) = (2) = 0,954; при t= 3, P= (  3) = (3) = 0,9973; при t= 4, P= (  4) = (4) = 0,99993.

11.3. Определение показателей выборки_•221

Тип 3. Определить необходимый объем выборки (n), который с за- данной достоверностью (вероятностью) (P) обеспечивает определен- ную точность выборочных характеристик.

Заданы или известны величины: P, ², ^{ x,} N, w, _p.

Формулы расчета необходимого объема выборки представлены в табл. 11.5.

Таблица 11.5

Расчет объема выборки

Показатели	Методы отбора единиц
	повторный	бесповторный
Объем выборки:
для средней, n	t22 2 x	t22N 2 N t22 x
для доли, n(в случаях, когда частость неиз- вестна, принимают w = 0,5)	t2w(1 w) 2 p	t2Nw(1  w) 2 N t2w(1  w) p

Рассмотрим методику исчисления объема выборки, ошибки вы- борки и других показателей на примере решения задач.

Задача 11.1. По результатам выборочного наблюдения (табл. 11.6) были получены следующие данные о величине денежных затрат по- сетителей кафе на один заказ.

Таблица 11.6

Результаты выборочного наблюдения

Стоимость заказа, тыс. руб.	До 1	1—3	3—5	5—7	7 и больше
Количество посетителей, человек	8	16	26	10	5

Наблюдение проводилось в форме механической повторной выборки. По данным выборочного наблюдения определим:

1. 
   какие денежные средства в среднем затрачивают посетители кафе на один заказ;
   
2. 
   среднюю ошибку выборочной средней;
   
3. 
   с вероятностью 0,954 предельную ошибку выборочной средней.
   

Решение. По данным выборочного наблюдения рассчитаем, сколь- ко денег в среднем затрачивают посетители кафе, оплачивая один за- каз (рассчитаем выборочную среднюю):

X^  ^Xf ²⁴⁰  3,692 тыс. руб.

_ f⁶⁵

Вывод. Один заказ (средний чек) составляет в среднем 3692 руб.

222_•глава 11. выбОрОчнОе наблюдение

Расчеты представлены в табл. 11.7.
Расчет средней ошибки выборочной средней

Таблица 11.7

Стоимость за- каза, тыс. руб.	Количество посе- тителей f, человек	X	X f	X X	(X X )2	(X X )2 f
А	1	2	3	4	5	6
До 1	8	0,5	4	–3,192	10,1889	81,5112
1—3	16	2,0	32	–1,692	2,8629	45,8064
3—5	26	4,0	104	+0,308	0,0949	2,4674
5—7	10	6,0	60	+2,308	5,3269	53,2690
7 и больше	5	8,0	40	+4,308	18,5589	92,7945
Итого:	65	Х	240	Х	Х	275,8485

Рассчитаем, на сколько рублей отличается средняя стоимость зака- за, исчисленная по результатам выборочного наблюдения, от реальной стоимости заказа, т.е. рассчитаем величину ошибки выборочной средней.

Средняя ошибка выборочной средней исчисляется по формуле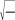


.
  ^2

n

Произведем расчет выборочной дисперсии (среднего квадрата откло- нений):

_(X X^ )² f

275,8485

²    4,24382.

_ f⁶⁵

Произведем расчет среднегоквадратическогоотклонения: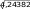

    2,060 тыс. руб.

Вывод. У отдельных посетителей кафе, попавших в выборку, сто- имость заказа отклоняется от средней величины заказа (по выборке) в среднем на 2060 руб.

Средняяошибкавыборочнойсредней:

  ^2 

n

4,24382 _

65
0,2555 тыс. руб.

Рассчитаем пределы, в которых находится размер заказа в генераль- ной совокупности:

x x^   3,692  0,256;

3,436  x 3,948.

3. 
   Определение показателей выборки_•223
   

Вывод. Посетители кафе делают заказ на сумму в среднем от 3436 до 3948 руб.

Рассчитаем предельную ошибку выборочной средней с вероятностью 0,954:

  t  2  0,256  0,512 тыс. руб.

Рассчитаем пределы, в которых находится генеральная средняя:

x x^   3,692  0,512;

3,180  x 4,204.

Вывод. С вероятностью 0,954 (в 954 случаях из 1000) можно утверж- дать, что посетители кафе делают заказ в среднем на сумму от 3180 до 4204 руб.

Задача 11.2. Сколько посетителей кафе нужно обследовать в по- рядке механической повторной выборки для определения среднего размера чека, чтобы с вероятностью 0,954 можно было гарантировать ошибку не более 150 руб.? Дисперсия по данным предыдущего обсле- дования — 4243,82.

Решение. Сделаем краткую запись исходных данных задачи:

P(t) = 0,954; t= 2; ² = 4243,82;  = 150 руб.

Рассчитаем количествопосетителейкафе, необходимое для обсле- дования в порядке механической повторной выборки для определения среднего размера чека (заказа):

_t2_2

n

_2

_ 2²  4243,82

150²
 76 человек.

Вывод. Для определения среднего размера заказа нужно обследо- вать 76 человек в порядке механической повторной выборки, чтобы с вероятностью 0,954 можно было гарантировать ошибку не более 150 руб.

Задача 11.3. По результатам выборочного обследования 65 посе- тителей кафе было установлено, что большинство посетителей кафе (85%) — женщины.

С вероятностью 0,954 определите пределы, в которых будет нахо- диться доля женщин в общем количестве посетителей кафе.

Решение. Сделаем краткую запись исходных данных задачи:

n= 65 человек; w= 0,85; P(t) = 0,954; t= 2.

224_•глава 11. выбОрОчнОе наблюдение

Рассчитаем предельнуюошибкувыборочнойдоли:

  t 

w(1w) _{ 2 }

n

^{0,85(10,85)}  0,044 или 4,4%;

65

p w  0,85  0,044; 80,6%  p  89,4%.

Вывод. С вероятностью 0,954 (в 954 случаях из 1000) можно утверж- дать, что доля женщин составляет от 80,6 до 89,4% общего количества посетителей кафе.