тест по статистике. Гладун И. В_Статистика СКАН. Учебника для использования в учебном процессе образовательных учреждений, реализующих программы спо

• Название: Учебника для использования в учебном процессе образовательных учреждений, реализующих программы спо
• Анкор: тест по статистике
• Дата: 27.09.2022
• Размер: 1.13 Mb.
• Имя файла: Гладун И. В_Статистика СКАН.docx
• Тип: Учебник; #699128
• страница: 43 из 50

Ответы: 1 — а; 2 — в; 3 — б; 4 — г; 5 — б; 6 — индексируемой вели- чиной; 7 — г; 8 — а.

глава10 СтАтИСтИчЕСкИЕ мЕтОДы ИЗучЕНИя ВЗАИмОСВяЗЕй

СОцИАЛЬНО-ЭкОНОмИчЕСкИх

яВЛЕНИй
Познание всякой вещи, если оно возникает, достигается и бывает совершенным через по- знание ее причин.

Ибн-Сина

1. 
   Статистическое изучение стохастических взаимосвязей
   

Любое явление формируется под воздействием множества причин (факторов). Например, на уровень успеваемости студентов колледжа влияют способности студентов, количество времени на подготовку к учебным занятиям, квалификация преподавателей и др. Одни при- чины (факторы) являются главными, определяющими в основном уровень успеваемости, другие — второстепенными, незначительно влияющими на успеваемость.

Изучение причинно-следственных связей между явлениями дает возможность лучше их понять, а следовательно, целенаправленно на них воздействовать.

Например, определив факторы, влияющие на успеваемость сту- дентов колледжа, можно разработать мероприятия по ее повышению: повысить мотивацию студентов или улучшить материально-техниче- скую базу, разнообразить формы учебных занятий или повысить от- ветственность студентов за нарушение дисциплины и др.

Перед статистикой стоят следующие задачи:

1. 
   выявить наличиеили отсутствие причинно-следственных связей между социально-экономическими явлениями;
   
2. 
   определить направлениесвязи;
   
3. 
   количественно измерить теснотусвязи;
   
4. 
   выразить математически формусвязи.
   

192_•глава 10. статистические метОды изучения взаимОсвязей...

Полученную информацию можно использовать:

1. 
   для глубокого анализасоциально-экономических явлений и про- цессов, в том числе финансово-хозяйственной деятельности предприятия,
   
2. 
   для выявления неиспользованных резервов;
   
3. 
   в планировании;
   
4. 
   в прогнозировании;
   
5. 
   в ходе разработки норм, нормативов.
   

Количественному анализу связей между явлениями должен пред- шествовать глубокий анализ сущности изучаемых явлений — каче- ственный анализ.

Типы зависимостей между явлениями многообразны (табл. 10.1).

Таблица 10.1

Характеристика взаимосвязей между явлениями

Статистическая категория

Содержание категории

Виды статистических признаков

Факторныйпри- знак Х	Независимый признак, влияющий на другие признаки и определяющий их значения
Результативный признак Y	Зависимый признак, изменяющийся под влиянием фак- торных признаков Х1, Х2, …, Хn

Типы взаимосвязей

Функциональная зависимость	Каждому значению признака-фактора (Х) соответствует однострого определенное значение Y
Стохастическая (вероятностная) зависимость	Каждому значению Хсоответствует рядзначений Y(Y1, Y2, …, Yn). Связь проявляется для совокупностивцелом, а не для каждой единицы совокупности в отдельности
Корреляционная зависимость	Частный случай стохастической связи: каждому значе- нию Хсоответствует среднеезначение Y(Y)

Виды взаимосвязей по направлению

Прямаясвязь	Если значения Х растут, значения Y тоже растут (и на- оборот). Например, если растет численность рабочих — растет и количество произведенной продукции (при про- чих равных условиях)
Обратнаясвязь	Если значения Храстут, значения Yуменьшаются(и на- оборот). Например, если растет себестоимость продук- ции — снижается прибыль (при прочих равных условиях)

Виды взаимосвязей по аналитическому выражению (уравнению)

Линейнаясвязь

Зависимость между признаками Хи Yвыражается в виде уравнения прямой линии (прямолинейная связь)

2. 
   регрессионно-корреляционный анализ_•193
   

Окончание

Статистическая категория	Содержание категории
Нелинейнаясвязь	Зависимость между Хи Yвыражается в виде уравнения кривой линии: параболы, гиперболы, показательной функции, др.

Для выявления и изучения стохастических связей используются различные методы (табл. 10.2).

Таблица 10.2

Методы выявления стохастической связи

Метод	Содержание
Метод парал- лельных рядов	Сопоставление рядов статистических показателей, отра- жающих значения признака-фактора Хи результативного показателя Y. Значения Х перечисляются либо в порядке возрастания, либо в порядке убывания (ранжированный ряд)
Графический метод	Значения Х и Y изображают на графике в форме корреля- ционного поля. По форме корреляционного облака опре- деляют наличие или отсутствие связи и ее форму
Аналитическая группировка	Производят группировку единиц совокупности по Х. Для каждой группы исчисляют среднее значение Y
Корреляцион- ный анализ	Количественное определение теснотыи направлениясвя- зи между признаками
Регрессионный анализ	Определение формысвязи, т.е. ее аналитического выра- жения (формулы)

2. 
   Регрессионно-корреляционный анализ
   

Регрессионно-корреляционный анализ (РКА) — наиболее глубо- кий метод изучения стохастических связей. Он заключается в постро- ении и анализе экономико-математической модели в виде уравнения регрессии, выражающего зависимость явления Yот определяющих его факторов Х₁, Х₂, …, Х_n.

Выделяют следующие этапыРКА:

1. 
   предварительный (априорный) анализ;
   
2. 
   сбор информации, ее первичная обработка;
   
3. 
   построение модели (уравнения) регрессии;
   
4. 
   оценка и анализ модели.
   

194_•глава 10. статистические метОды изучения взаимОсвязей...

На первом этапе РКА формулируют цель, задачи исследования, определяют результативный признак Yи показатель, его отражающий, выявляют признаки-факторы Х₁, Х₂, …, Х_n, оказывающие наиболее су- щественное влияние на формирование результативного признака, ме- тодику их измерения. Желательно, чтобы факторные признаки имели количественное выражение и не дублировали друг друга.

Для обеспечения надежных результатов исследования собирают достаточно большой массив качественно однородных данных (вто- рой этап РКА). Объем совокупности (число единиц) должен быть в 6—8 раз больше количества включаемых в модель факторов. Далее проводят оценку однородности совокупности, проверку соответствия распределения факторных признаков критериям нормального распре- деления, исключают при необходимости аномальные единицы.

Качественная однородность собранных данных предполагает су- ществование близких условий формирования результативного и фак- торных признаков. Например, при изучении факторов, определяющих успеваемость студентов колледжа, не следует объединять в одну сово- купность студентов дневного и заочного отделений.

Для количественной оценки однородности совокупности исполь- зуют коэффициент вариации по факторным признакам:
V ^x 100%, x_x

i

где _x— среднее квадратическое отклонение факторного признака;

24. 
    — среднее значение факторного признака.
    

Совокупность считается однородной, если коэффициент вариации

V_xменьше 33%.

Проверка первичных данных на нормальность распределения про- водится с помощью правила «трех сигм»: ^{xi  3 x}(см. решение задачи 10.1).

Из совокупности исключают (при необходимости) аномальныееди- ницы — единицы наблюдения, у которых значение признака-фактора не удовлетворяет неравенству ^{xi  3 x  xi  xi  3 x.}

На третьем этапе РКА при построении уравнения регрессии (мо- дели) устанавливают наличие корреляционной связи между результа- тивным показателем и факторами, определяют ее форму, направление, измеряют степень тесноты и существенности связи.

Формасвязи— это тип аналитической функции, характеризующей механизм взаимосвязи между результативным признаком и признака- ми-факторами. Например, прямая линия, парабола второго порядка,

10.2. регрессионно-корреляционный анализ_•195

гипербола, др. (см. табл. 10.7). Выбор формы связи производят на ос- нове теоретического и эмпирического анализа.

Сделать обоснованный выбор уравнения регрессии только на осно- ве теоретического анализа очень трудно, так как изучаемые социаль- но-экономические явления сложны по своей структуре, внутренняя логика их связей не всегда ясна, факторы взаимодействуют не только с результативным показателем, но и друг с другом, информация о них неполная.

Поэтому теоретический анализ дополняется эмпирическим. Если нанести в виде точек исходные данные, отражающие стохастическую зависимость между результативным показателем Y и признаком-фак- тором Х на график в прямоугольной системе координат, то получают совокупность точек, которая представляет собой не линию, а «обла- ко», в котором каждому значению Х соответствует не одно (как при функциональной связи), а несколько значений Y. Это «облако» или поле корреляции помогает определить направление связи (прямая, об- ратная), форму связи и др.

Эмпирическая линия регрессии графически отображает изменение групповых средних результативного признака (^Yi) в зависимости от изменения признака-фактора (Х) и предоставляет дополнительную

информацию для РКА.

Обоснованно выбрав форму корреляционной связи, исчисляют па- раметры модели (уравнения регрессии).

На четвертом этапе РКА осуществляется оценка и анализ постро- енной модели.

На основании уравнения регрессии определяются теоретические значения результативного признака (^Yx ), т.е. значения Y при условии, что на него влияет только один фактор Х₁, а другие факторы Х₂, Х₃, …,

Х_nостаются на неизменном уровне.

Расчет параметров уравнения регрессии основан на методе наи- меньших квадратов, согласно которому сумма квадратов отклонений эмпирических значений Y от теоретических ^Yxминимальна:

S _(YY_x)²  min.

В случае выравнивания по прямой метод наименьших квадратов приводит к следующей системе нормальных уравнений:

^_na₀  a_{1 } x _ y

^a x ax²  yx<sup>.

</sup>_ 0  1  

196_•глава 10. статистические метОды изучения взаимОсвязей...

Параметры а₀ и а₁ определяют по формулам

a₀  y a₁x;

_{a }xynxy_.

¹ _ x²  nx²

Для определения параметров параболы второго порядка Y= a₀ +

+ a₁x+ a₂x² система нормальных уравнений такова:

^na₀  a_{1 } x a_{2 } x²  _ y

^a x ax²  ax³  yx.

^ 0  1  2  

^ax²  ax³  ax⁴ 

yx²

_ 0  1  2  

Для оценки степени точности отражения изучаемой взаимосвязи между X и Y исчисляют следующие показатели:

^Se100%;

y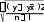
S_e ,
где S_e— средняя квадратическая ошибка уравнения;

24. 
    — средний уровень результативного признака;
    

y— фактические значения результативного признака;

^yx— значения результативного признака, рассчитанные по урав- нению регрессии;

n— количество единиц наблюдения;

l— число параметров в уравнении регрессии.

Если отношение ^Se100% не превышает 10—15%, то уравнение ре-

y

грессии хорошо отображает изучаемую стохастическую взаимосвязь.

Теснота корреляционной связи между социально-экономическими явлениями изучается с помощью таких показателей, как линейный ко- эффициент корреляции, эмпирическое корреляционное отношение и др. (табл. 10.3).

Для определения тесноты связи между альтернативными призна- ками, имеющими любое число вариантов значений, используются коэффициент взаимной сопряженности К. Пирсона и коэффициент взаимной сопряженности А.А. Чупрова.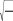

10.2. регрессионно-корреляционный анализ_•197

Таблица 10.3

Методика определения степени тесноты корреляционной связи

Показатель	Формула расчета	Условие применения
Линейный коэффици- ент корре- ляции	r (xx)(yy)  nx y  xy xy  n,   x2    y2   x2    y2    n  n где x x— отклонения вариантов значений признака-фактора от их средней величины; y y— отклонения вариантов значений резуль- тативного признака от их средней величины; x, y— среднее квадратическое отклонение признака-фактора и результативного признака соответственно	Парная линейнаяза- висимость между Yи X
Эмпириче- ское корре- ляционное отношение	  2 , 2 y где 2 — межгрупповая дисперсия результативного признака, вызванная влиянием признака-фактора; 2 — общая дисперсия результативного признака y	Парная нели- нейная(кри- волинейная) зависимость между Y и X
Коэффи- циент Фех- нера	K CH, ф C  H где С, Н — соответственно количество со- впадений и несовпадений знаков отклонений индивидуальных величин факторного признака Х и результативного признака Y от их средней арифметической величины соответственно. 1,0  Kф  1,0	При неболь- шом объеме исходной информации
Коэф- фициент корреля- ции рангов Спирмэна	6d2   1 i, n(n2 1) где di— разность между величинами рангов при- знака-фактора и результативного признака; n— число показателей (рангов) изучаемого ряда. –1,0    +1,0	Для коли- чественных и качествен- ных призна- ков, значе- ния которых могут быть проранжи- рованы

198_•глава 10. статистические метОды изучения взаимОсвязей...

Окончание

Показатель	Формула расчета	Условие применения
Коэф- фициент ассоциации Д. Юла	K adbc K, A ad bcK где a, b, c, d— частоты взаимного сочетания двух альтернативных признаков А и В	Для каче- ственных альтернатив- ных призна- ков
Коэффи- циент кон- тингенции К. Пирсона	K adbc K, K(a b)(b d)(a c)(c d) A где a, b, c, d— частоты взаимной комбинации двух альтернативных признаков А и В

В таблице 10.4 отражено содержание основных категорий корреля- ционного анализа.

Таблица 10.4