Мех_нефиз_240_24.10.2011. Мех_нефиз_240_24.10. Учебнометодический комплекс по дисциплине для нефизических специальностей Лабораторный практикум Абакан 2011 ббк 22. 2я73

• Название: Учебнометодический комплекс по дисциплине для нефизических специальностей Лабораторный практикум Абакан 2011 ббк 22. 2я73
• Анкор: Мех_нефиз_240_24.10.2011.doc
• Дата: 09.05.2017
• Размер: 1.9 Mb.
• Имя файла: Мех_нефиз_240_24.10.2011.doc
• Тип: Учебно-методический комплекс; #7342
• страница: 2 из 12

Контрольные вопросы

1. 
   Что такое масса тела и чем она отличается от веса тела?
   
2. 
   Зависят ли масса тела и вес тела от широты местности и почему?
   
3. 
   Что такое плотность твердого тела и что она характеризует?
   
4. 
   Что такое прямые и косвенные измерения?
   
5. 
   Дайте определение нониуса и его точности.
   
6. 
   Расскажите об устройстве и правилах использования штангенциркуля.
   
7. 
   Расскажите об устройстве технических весов и правилах взвешивания на них.
   
8. 
   Как определить точность взвешивания на технических весах в грубом приближении? Какова погрешность взвешивания в этом случае?
   

Лабораторная работа 2
ОПРЕДЕЛЕНИЕ ПЛОТНОСТИ

СЕЛЬСКОХОЗЯЙСТВЕННЫХ ПРОДУКТОВ

В ТВЁРДОМ, ЖИДКОМ И СЫПУЧИХ СОСТОЯНИЯХ
Цели работы: изучить устройство технических весов и приобрести навыки их использования; определить плотность сельскохозяйственных продуктов в твердом, жидком и сыпучем состояниях; определить процентное содержание крахмала в картофеле.

Приборы и принадлежности: весы технические с набором гирь, мензурка, мерный стакан, сельскохозяйственные продукты (например, картофель, пшеница, раствор поваренной соли).

Библиографический список: [3] § 39; [7] § 1.3.1; [8] § 5.
Введение

Распределение массы в пределах тела можно охарактеризовать с помощью величины, называемой плотностью. Если тело однородно, т.е. свойства его во всех точках одинаковы, то плотностью называется величина, равная:

, (2.1)

где m – масса тела, а V– его объём.

Для тела с неравномерно распределенной массой выражение (2.1) дает среднюю плотность. В этом случае плотность в точке тела определяется следующим образом:

, (2.2)

где Δm – масса, заключенная в объёме ΔV.

Предельный переход в этом выражении нельзя понимать так, что объём ΔV стягивается буквально в точку. Уменьшение ΔV следует осуществлять до тех пор, пока ещё не обнаруживается атомная структура вещества. Поэтому под dV в (2.2) надо подразумевать физически бесконечно малый объём, который, с одной стороны, достаточно мал для того, чтобы макроскопические (т.е. присущие большой совокупности атомов) свойства вещества можно было считать в его пределах одинаковыми, а с другой стороны, достаточно велик для того, чтобы не могла проявляться дискретность (прерывность) вещества.

Согласно (2.2) элементарная масса dm равна произведению плотности ρ тела в данной точке на соответствующий элементарный объём dV:

dm = ρdV . (2.3)

Тогда масса всего тела равна:

, (2.4)

где интегрирование распространяется на весь объём V тела.

Введя понятие плотности вещества, необходимо раскрыть его практическое значение. Определение плотности вещества на практике имеет разное назначение. Это связано с тем, что во многих случаях с изменением составных частей сложного вещества происходит изменение плотности этого вещества. Поэтому оказывается возможным по величине плотности судить о том, состоит ли данное тело из одного вещества или содержит примеси других. В сложных, например, органических веществах по плотности можно определить процентное содержание составляющих веществ. Так, по плотности молока определяют процентное содержание в нем жира и белков.

Существует также определенная зависимость плотности картофеля от количества содержащихся в нем крахмала и белков. Учитывая характер этой зависимости, по плотности картофеля определяют процентное содержание в нем крахмала. Последнее дает возможность решить вопрос о том, где целесообразнее использовать данный сорт картофеля.

Картофель, содержащий крахмал менее 20 % от массы всего клубня, идет на корм скоту. Картофель с большим содержанием крахмала, лучше использовать для технических целей, например, для переработки на крахмал и патоку. Почти с такой же крахмалистостью нужен картофель и для питания человека.
Теория метода измерений

В данной лабораторной плотности тела определяется по формуле (2.1). Масса и объём, необходимые для нахождения плотности пшеницы, картофеля и жидкости, измеряются экспериментально с помощью весов и мензурки.

Нахождение массы сыпучих веществ и растворов можно производить несколькими способами. Можно определить массу образца взвешиванием его в сосуде с известной массой (если масса сосуда не известна, то её необходимо найти). В этом случае масса тела (m_т) равна:

m_т = m_п – m_с (2.5)

где m_п – масса сосуда вместе с телом, и m_с – масса сосуда, в котором взвешивают образец.

Другой способ заключается в том, что массой сосуда можно пренебречь, если масса тела велика по сравнению с массой сосуда. Например, сыпучие вещества массой 100 г насыпают в полиэтиленовый пакет.

Массу жидких веществ можно определить этими же двумя способами, а массу картофеля – путем взвешивания клубня на весах.

При определении объема твердого тела можно воспользоваться методом Архимеда, т.е. приравнять объем твердого тела к объему жидкости, вытесненной этим телом. Тогда объём картофеля:

ΔV = V₁ – V₀ , (2.6)

где V₀ – объём жидкости в мензурке до погружения картофеля, а V₁ – объём, занимаемый жидкостью вместе с погруженным в нее картофелем.

Объёмы сыпучих веществ и жидкости определяется с помощью мерного стакана.
Измерения и обработка результатов

1. 
   Ознакомиться с устройством технических весов и правилами взвешивания (см. лабораторную работу 1).
   
2. 
   Определить массу, объём и плотность сельскохозяйственных продуктов. Результаты измерений и вычислений занести в таблицу 2.1.
   

Таблица 2.1

Исследуемый продукт	m, 10-3 кг	V, 10-6 м3	ρ, кг/м3

3. 
   Определить процентное содержание крахмала в картофеле (см. приложение 2). Сделать вывод о целесообразности использования данного сорта картофеля.
   
4. 
   Определить насыпную плотность пшеницы. Полученное значение плотности сравнить с табличным (ρ_пш = 760 кг/м³) и сделать вывод о причинах отклонения от табличного значения.
   
5. 
   Определить плотности растворов поваренной соли (NaCl) с различными концентрациями. Построить график зависимости плотности раствора от концентрацииNaCl в этом растворе.
   

Контрольные вопросы

1. 
   Что такое плотность твердого тела и что она характеризует?
   
2. 
   Что такое прямые и косвенные измерения?
   
3. 
   Расскажите об устройстве технических весов и правилах взвешивания на них.
   
4. 
   Как определить точность взвешивания на технических весах в грубом приближении? Какова погрешность взвешивания в этом случае?
   
5. 
   Где можно применять на практике в сельском хозяйстве знание плотности вещества?
   

ЦИКЛ 2. КИНЕМАТИКА

И ДИНАМИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ.

ЗАКОНЫ СОХРАНЕНИЯ
Лабораторная работа 3
ИЗУЧЕНИЕ ЗАКОНОВ РАВНОУСКОРЕННОГО ДВИЖЕНИЯ

С ПОМОЩЬЮ МАШИНЫ АТВУДА
Цели работы: изучение законов движения грузов на машине Атвуда и ознакомление с простейшими методами экспериментальной проверки функциональной зависимости между измеряемыми величинами.

Приборы и принадлежности: машина Атвуда, набор дополнительных грузов, секундомер.

Библиографический список: [1] § 3; [2] ч.1 § 4, § 5; [3] т.1 § 4; [4] т.1 § 2; [5] § 1.5; [7] § 1.2.1; [8] § 2.
Введение

Р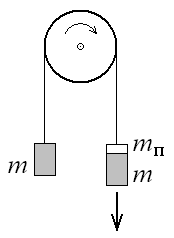ассмотрим движение системы 2-х тел одинаковой массы m, которые подвешены к концам нити, перекинутой через блок (рис. 3.1). Грузы могут двигаться вдоль вертикального направления. Если на один из грузов положить небольшой добавочный груз (перегрузок) массой m_п, то грузы начнут двигаться с ускорением а под действием силы тяжести. Такое движение называют равноускоренным, т.е. движение с постоянным по модулю и направлению ускорением ().

Е
Рис. 3.1
сли система тел начинает движение из состояния покоя, то пройденный системой путь S за время t определяется формулой:

. (3.1)

Справедливость уравнения (3.1) в данной работе можно проверить с помощью машины Атвуда двумя способами:

1. 
   Графический метод. Теоретическая формула (3.1) является нелинейной (квадратичной) зависимостью между S и t. Но для переменной x =t² эта зависимость становится линейной, а ее график (в координатах S и t²) – прямой, проходящей через начало координат. Следовательно, если график, построенный по результатам измерений в координатах S и t², можно представить в виде прямой, проходящей через начало координат, то для движения грузов справедлива проверяемая формула (3.1), движение грузов является равноускоренным и можно вычислить ускорение а.
   
2. 
   Аналитический метод. Проверка формулы (3.1) без построения графика заключается в том, что в ходе эксперимента для различных расстояний S₁,S₂, S₃, S₄ проходимых грузами под действием одинаковой силы (m_п = const) вычисляются ускорения а₁, а₂, а₃, а₄ по формуле (3.1). Если их отклонения (относительные погрешности) от среднего значения а_ср не превосходят 10 %, то в пределах такой погрешности эти ускорения можно считать одинаковыми, а движение – равноускоренным и проверяемую формулу справедливой.
   

Описание экспериментальной установки

У
Рис. 3.2. Машина Атвуда
становка, называемая машиной Атвуда (рис. 3.2), представляет собой вертикальную стойку с сантиметровой шкалой 1 и регулировочными винтами 2. На верхнем конце стойки прикреплен легкий пластмассовый блок 3, через который переброшена нить с подвешенными на концах грузами m₁ и m₂. Массы грузов примерно одинаковы, за счет трения в блоке система находится в равновесии. Для того, чтобы привести систему грузов в движение, на правый груз кладут перегрузок m_п. Опуская левый груз, устанавливают начальное положение правого груза на определенном делении шкалы. Время движения грузов определяется с помощью механического секундомера. Для начала измерения опускают левый груз и одновременно включают секундомер. Момент отключения секундомера должен совпадать со звуком удара правого груза о дно приемного столика 4.
Измерения и обработка результатов

Упражнение 1. Графический метод проверки справедливости уравнения перемещения.

1. 
   Привести установку в рабочее состояние. Для этого установить шкалу 1 в вертикальном положении при помощи регулировочных винтов. Правильность установки проверяется по падению груза m₂ в приемный столик 4.
   
2. 
   Поместить на правый груз перегрузки, достаточные для того, чтобы компенсировать силу терния в блоке 3 и создать равноускоренное движение.
   
3. 
   Измерить время движения грузов для четырех значений перемещения (для каждого расстояния время нужно измерить три раза).
   
4. 
   Результаты измерений и вычислений занести в таблицу 3.1.
   

Таблица 3.1

№ опыта	Перемещение S, м	Время движения грузов				Квадрат времени , с2
		t1, с	t2, с	t3, с	tср, с
1
2
3
4

5. 
   Построить график зависимости S от .
   
6. 
   Сделать вывод о справедливости (или несправедливости) формулы (3.1) для движения грузов на машине Атвуда.
   
7. 
   Рассчитать ускорение грузов a_граф с помощью формулы (3.1) по неэкспериментальной точке, лежащей на прямой линии.
   

Упражнение 2. Аналитический метод проверки справедливости уравнения перемещения.

1. 
   Используя экспериментальные данные для перемещения и времени, полученные в упражнении 1, вычислить ускорения а₁, а₂, а₃, а₄ по формуле (3.1).
   
2. 
   Определить среднее значение ускорения а_ср.
   
3. 
   Найти отклонения от среднего значения (индекс i соответствует номеру измерения) и относительную погрешность измерений по формуле:
   

.

4. 
   Результаты измерений и вычислений занести в таблицу 3.2.
   

Таблица 3.2

№ опыта	S, м	а, м/с2	Δа, м/с2	ε, %
1
2
3
4
ср.	–			–

5. 
   Сделать вывод о справедливости (или несправедливости) формулы (3.1) для движения грузов на машине Атвуда.
   
6. 
   Экспериментальное значение ускорения представить в виде:
   

а = а_ср ± Δа_ср.

Контрольные вопросы

1. 
   Какое движение называют равноускоренным?
   
2. 
   Дайте определение ускорения. Какие виды ускорения вам известны?
   
3. 
   Запишите формулы перемещения и скорости при равноускоренном движении, в том числе, при начальных условиях: υ₀ = 0.
   
4. 
   Изобразите примерные графики зависимостей перемещения от времени (S от t), модуля скорости от времени (υ от t), перемещения от квадрата времени (S от t²) и скорости от корня квадратного из перемещения (υ от).
   
5. 
   Каков метод определения ускорения используется в данной работе?
   

Лабораторная работа 4
ПРОВЕРКА УРАВНЕНИЙ РАВНОУСКОРЕННОГО ДВИЖЕНИЯ
Цели работы: проверить уравнение перемещения при равноускоренном движении; проверить второй закон Ньютона; найти мгновенную скорость.

Приборы и принадлежности: электрифицированная машина Атвуда, выпрямитель, электронный секундомер, ключ коммутационный, соединительные провода, перегрузки различной массы.

Библиографический список: [1] § 3, § 6; [2] ч.1 § 4, § 5, § 7; [3] т.1 § 4, § 9, § 17; [4] т.1 § 2 - 3; [5] § 1.5, § 2.2; [7] § 1.2.1, § 1.3.1.
Введение

Рассмотрим движение системы, состоящей из двух тел одинаковой массы М с перегрузком m на одном из них; тела подвешены к концам нити, перекинутой через блок (рис. 4.1).

Б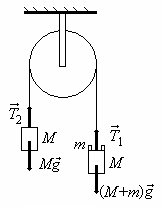ез учета трения второй закон для первого тела запишется в виде:

(М + m)g – T₁ = (M + m)a₁ (4.1)

Для второго тела:

Т₂ – Mg = Ма₂ (4.2)

Е
Рис. 4.1
сли нить нерастяжима, а массами нити и блока можно пренебречь, то грузы движутся с одинаковыми ускорениями и силы натяжения, действующие на грузы, одинаковы. Отсюда из (4.1) и (4.2) получим:

mg = (2M + m)a. (4.3)

Если силой трения пренебречь нельзя, то уравнение (4.3) примет вид:

Mg – F_тр = (2M + m)a. (4.4)

Если система тел начинает движение из состояния покоя, для перемещения S и скорости υ справедливы уравнения:

, (4.5)

υ = аt. (4.6)

Из (4.5) и (4.6) формул можно получить зависимость υ от S:

υ ² = 2aS. (4.7)
Описание экспериментальной установки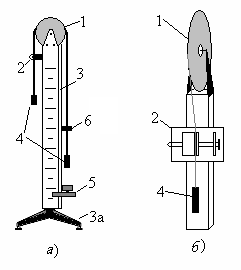




Электрифицированная машина Атвуда состоит (рис. 4.2) из:

• 
  легкого пластмассового блока 1;
  
• 
  электромагнитного пускателя 2;
  
• 
  вертикальной стойки 3, укрепленной на подставке с регулировочными винтами (3а); на стойке имеется сантиметровая шкала;
  
• 
  системы грузов 4;
  
• 
  приемного столика 5;
  
• 
  подвижного кольца 6.
  

Рис. 4.2. Машина Атвуда

Н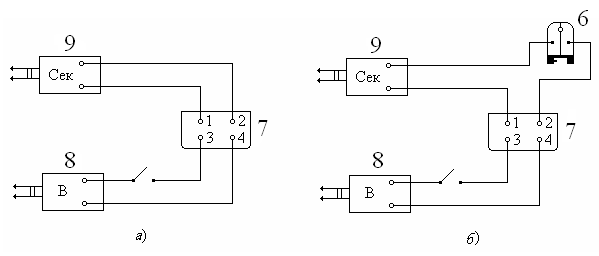
Рис. 4.3. Блок-схема
а оборотной стороне стойки 3 имеется специальный паз с токоведущими шинами и колодкой 7 (рис. 4.3); колодка предназначена для подключения к машине Атвуда источника переменного тока 220 В (через селеновый выпрямитель 8) и счетчика-секундомера 9. Подключают эти приборы по блок-схеме (рис. 4.3а) или по блок-схеме (рис. 4.3б).

Электромагнитный пускатель 2 служит для начальной фиксации грузов 4, укрепленных на нити. Нить перекинута через блок 1 и при проведении опытов располагается между якорем и сердечником электромагнита (рис. 4.2а).

При подаче напряжения якорь электромагнита притягивается к сердечнику, и нить надежно захватывается, фиксируя требуемое положение грузов 4. Приемный столик 5 предназначен для разрыва электрической цепи счетчика-секундомера в момент приема падающего на него груза 4.

Грузы 4 состоят из 2-х частей (нижняя часть отвинчивается при необходимости). Внутри каждого груза имеется набор маленьких шариков. Варьируя их количество, можно добиться одинаковой массы грузов. К машине Атвуда прилагаются перегрузки различной массы. Меняя перегрузки, изменяют силу, действующую на систему грузов. Отвинчивая нижние части грузов 4, изменяют массу движущейся системы.

Подвижное кольцо 6 используют, когда возникает необходимость снятия перегрузка с правого груза 4. Сверху подвижное колесо снабжено двумя металлическими полукольцами, выполняющими роль контактов при падении на них перегрузов. В этот момент включается счетчик-секундомер 9 (см. блок-схему рис. 4.3б). Кольцо крепится на столике 3 (рис. 4.1) на пути движения правого груза 4.
Теория метода измерений

Проверка уравнения перемещения и определение мгновенной скорости

Для проверки уравнения перемещения равноускоренного движения используют блок-схему на рисунке 4.3а, определения скорости – блок-схему на рисунке 4.3б. В обоих случаях равноускоренное движение вызывается одним и тем же перегрузком (перегрузками).

При проведении лабораторной работы необходимо на правый груз поместить два перегрузка (m и m^/). Требования к перегрузкам: нижний перегрузок, например, m^/ должен компенсировать силу трения в оси блока и нити о блок; линейные размеры верхнего перегрузка должны быть таковы, чтобы он не проходил через подвижное кольцо 6.

Если трение хорошо скомпенсировано, то в случае блок-схемы (рис. 4.3б) движение правого груза 4 до кольца 6 равноускоренное, после кольца – равномерное. Очевидно, конечная скорость υ равноускоренного движения равна скорости υ* равномерного движения (υ = υ*), причем:

υ = аt, (4.8)

. (4.9)

Здесь tи t* – время движения правого груза до и после кольца, S* – перемещение груза после кольца.

В данной работе мгновенную скорость определяют по формуле (4.9).

Проверка второго закона Ньютона

Рассмотрим движение системы грузов 4 с двумя перегрузками m₁ и m₂. Вначале поместим оба перегрузка на правый груз, затем меньший перегрузок (например, m₂) переложим на левый груз. При этом масса системы грузов 4 с перегрузками не изменится, а сила, действующая на эту систему, изменится. Из уравнения (4.4) для этих случаев имеем:

(m₁ + m₂)g – F_тр = (2M + m₁ + m₂) а₁, (4.10)

(m₁ – m₂)g – F_тр = (2M + m₁ + m₂) а₂. (4.11)

Из (4.10) и (4.11):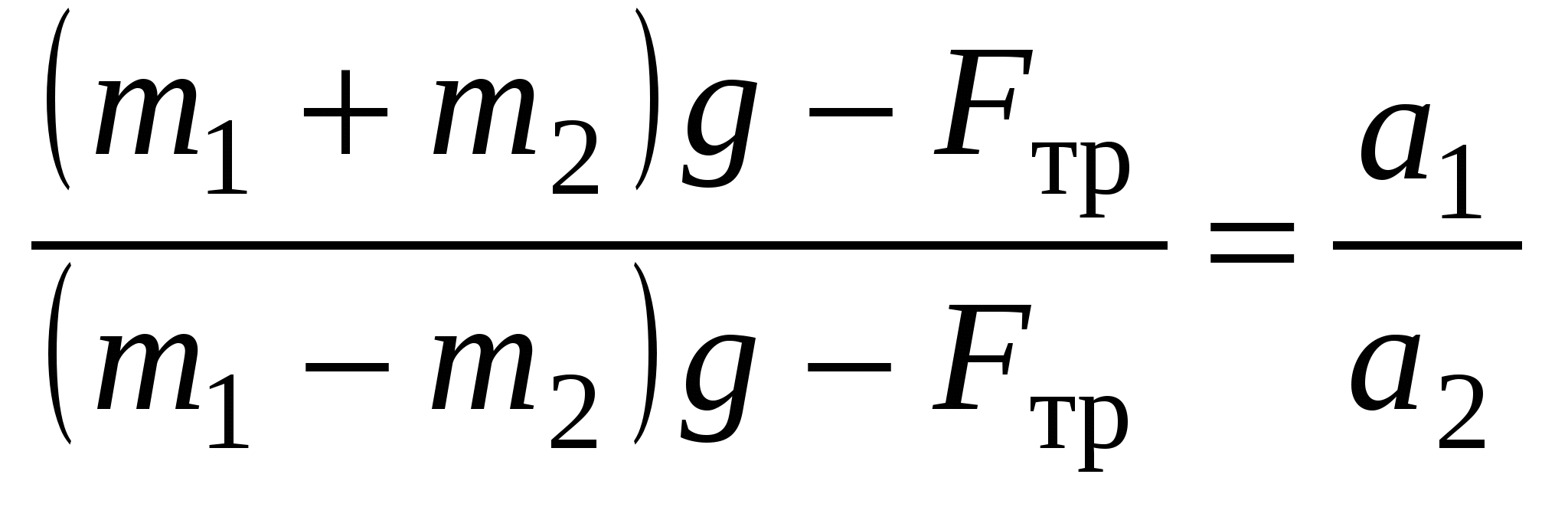

. (4.12)

Оставив перегрузки m₁ и m₂ на своих местах (m₂ на левом грузе, m₁ – на правом), уменьшим массу грузов 4 (отвинтим их нижние части). Сила трения при этом изменится (обозначим её F^/_тр). Из (4.4) для этого третьего случая получим:

(m₁ – m₂)g – F^/_тр = (2M^/ + m₁ + m₂) а₃. (4.13)

Здесь 2M^/ – масса грузов 4 без нижней части (облегченные грузы).

Так как силы трения F_тр и F^/_тр малы по сравнению с (m₁ – m₂)g, то ими можно пренебречь. Тогда сила, действующая на систему грузов 4 во втором и третьем случаях, одинакова.

Поэтому из (4.11) и (4.13):

. (4.14)

Проверка второго закона Ньютона сводится к проверке равенств (4.12) и (4.14).
Правила работы на машине Атвуда

1. 
   Установить стойку 3 в вертикальном положении при помощи регулировочных винтов 3а. Правильность установки проверяется по падению груза 4 в середину приемного столика 5 (рис. 4.2).
   
2. 
   Проверить правильность расположения нити грузов 4 в электромагнитном пускателе 2 (рис. 4.2а).
   
3. 
   Соединить машину Атвуда со счетчиком-секундомером 9 и выпрямителем 8 по нужной блок схеме. Коммутационный ключ (рис. 4.3а и 4.3б) при этом должен быть разомкнут.
   
4. 
   Правильность соединения и готовность прибора к работе дать проверить лаборанту.
   
5. 
   Включить секундомер 9 и выпрямитель 8 в сеть, а так же включить тумблеры «ВКЛ» секундомера и выпрямителя. Выходное напряжение на выпрямителе должно быть не более 6 В.
   
6. 
   Расположить грузы 4 с перегрузком на правом грузе так, чтобы нижнее основание правого груза было у нужного деления шкалы 3 и зафиксировать это положение. Для этого подать напряжение на электромагнитный пускатель 2, замкнув коммутационный ключ К.
   
7. 
   Приподнять площадку приёмного столика 5, нажав на его выступ в нижней части.
   
8. 
   Произвести установку «нуля» секундомера, для чего нажать кнопку «установка нуля» на секундомере, расположенную сверху.
   
9. 
   Разомкнуть коммутационный ключ К и тем самым освободить нить с грузами 4 и запустить секундомер.
   
10. 
    Перед началом каждого измерения повторить пункты 5 – 8.
    

Измерения и обработка результатов

Упражнение 1. Проверка уравнения перемещения.

1. 
   Подготовить установку к работе, используя блок-схему на рисунке 4.3а и инструкцию «Правила работы на машине Атвуда».
   
2. 
   Проверить уравнение пути равноускоренного движения:
   
   1. 
      подобрать два необходимых перегрузка (требования к ним указаны выше);
      
   2. 
      измерить время для 4-5 значений S(для каждого значения S опыт провести не менее трёх раз).
      
3. 
   Данные измерений занести в таблицу 4.1.
   

Таблица 4.1

№	1	2	3	4	5
S,
t,
tср.,
t2ср.,

4. 
   Построить график зависимости S от t².
   
5. 
   Сделать вывод о справедливости (или несправедливости) формулы (4.5) для движения грузов на машине Атвуда.
   

Упражнение 2. Определение мгновенной скорости.

1. 
   Заменить блок-схему рис. 4.3а блок-схемой рис. 4.3б и измерить время t* равномерного движения для 4-5 значений S*. Время каждого перемещения должно быть измерено не менее трёх раз. Суммарное перемещение до и после кольца 6 должно оставаться постоянным.
   
2. 
   Данные измерений занести в таблицу 4.2.
   

Таблица 4.2

	1	2	3	4	5
S*,
t*,
t*ср.,
Sср.,
υ,

3. 
   По формуле (4.9) вычислить конечную скорость равноускоренного движения грузов для различных S. Значения υ занести в таблицу 4.2.
   
4. 
   По данным таблицы 4.2 построить график зависимости υ от .
   
5. 
   Сделать вывод о справедливости (или несправедливости) формулы (4.7) для движения грузов на машине Атвуда.
   

Упражнение 3. Проверка второго закона Ньютона.

1. 
   Собрать блок-схему, представленную на рис. 4.3а.
   
2. 
   Определить силу трения (F_тр = m^/g). Для этого подобрать перегрузки m^/, компенсирующие трение при движении необлегченных грузов 4, и взвесить их.
   
3. 
   Убрать перегрузки m^/. Подобрать два других перегрузка m₁ и m₂ таких, чтобы разность их масс (m₁–m₂) была больше массы перегрузка m^/ и время t₃ движения облегченных грузов было не менее 2 секунд.
   
4. 
   Измерить время движения грузов 4 для трех случаев:
   
   1. 
      движутся необлегченные грузы, при этом на правом грузе лежат перегрузки m₁ и m₂ (время движения t₁);
      
   2. 
      движутся те же грузы, но перегрузок m₂ переложен на левый груз (время движения t₂);
      
   3. 
      движутся облегченные грузы, при этом на правом грузе лежит перегрузок m₁, на левом – m₂ (время движения t₃).
      

Время движения грузов в каждом случае определить не менее трех раз. Длина пути S при всех измерениях не меняется.

5. 
   Данные всех измерений занести в таблицу 4.3.
   

Таблица 4.3

№	m/,	m1,	m2,	2М,	2М/,	t1,	t2,	t3,
1 2 3
ср.

6. 
   Используя t_ср для каждого случая вычислить соответствующие ускорения (а₁, а₂, а₃) по формуле (4.8).
   
7. 
   Проверить справедливость равенств (4.12) и (4.14).
   

Контрольные вопросы

1. 
   Какое движение называют равноускоренным?
   
2. 
   Дайте определение ускорения. Какие виды ускорения вам известны?
   
3. 
   Запишите формулы перемещения и скорости при равноускоренном движении, в том числе при начальных условиях υ₀ =0.
   
4. 
   Изобразите примерные графики зависимости перемещения от времени (Sот t), скорости от времени (υ от t), перемещения от квадрата времени (Sот t²), (υ от ).
   
5. 
   Как определяется мгновенная скорость грузов в данной работе?
   
6. 
   Что такое сила? Как ее можно охарактеризовать?
   
7. 
   Сформулируйте и запишите второй закон Ньютона.
   
8. 
   Получите равенства (4.4), (4.12), (4.14).
   
9. 
   Как проверяется в работе справедливость 2-го закона Ньютона?
   
10. 
    Как в работе определяют (компенсируют) силу трения?
    

Лабораторная работа 5
ОПРЕДЕЛЕНИЕ СКОРОСТИ ПУЛИ
Цель работы: определение скорости пули с помощью баллистического маятника.

Приборы и принадлежности: баллистический маятник, баллистический пистолет и пуля, сантиметровая шкала, технические весы с разновесом.

Библиографический список: [1] § 9, § 13, § 15; [2] ч.1 § 9, § 18; [3] т.1 § 24, § 27–28; [4] т.1 § 4 - 6; [5] § 2.9, § 4.1, § 4.5; [7] § 1.4.1; [8] § 16, § 21.
Введение

Баллистический маятник – симметричное массивное тело, подвешенное на практически нерастяжимых нитях (рис. 5.1). Рассмотрим систему: баллистический маятник – пуля. Начальное состояние этой системы: маятник висит на нитях, пуля летит вдоль оси симметрии маятника со скоростью . Конечное состояние: маятник с застрявшей в нём пулей максимально отклонился от положения равновесия на угол α, центр тяжести С маятника поднялся на высоту h (рис. 5.2а).

При неупругом центральном ударе пули и маятника по закону сохранения импульса имеем:

. (5.1)

Если период маятника намного больше времени взаимодействия маятника с пулей, он успевает отклониться от положения равновесия и начинает движение из этого положения со скоростью . Это движение маятника с пулей, застрявшей в нём. Оно в отсутствие сопротивления воздуха и трения в подвесе маятника происходит в соответствии с законом сохранения механической энергии:

, (5.2)

где М и m – массы маятника и пули, h – максимальная высота подъема маятника с пулей. Из (5.1) и (5.2) следует

. (5.3)
Описание экспериментальной установки

Баллистический маятник, используемый в работе, представляет собой металлическую коробку 1 с указателем 5, подвешенную на двойном бифилярном подвесе 2 (рис. 5.1). Масса маятника намного больше массы пули.

Чтобы удар пули 3 и маятника был неупругим, коробка наполняется ватой или пластилином. На некотором расстоянии от маятника у
Рис. 5.1. Схема экспериментальной

установки
станавливают баллистический пистолет таким образом, чтобы удар пули с маятником был центральным (скорость пули направлена по оси маятника). Высоту подъема маятника h в данной работе определяют по максимальному смещению маятника S по шкале 4 (рис. 5.1). Из прямоугольного треугольника C₁OA (рис. 5.2б), где C₁O = L и C₁A = S имеем:

. (5.4)

Отсюда

. (5.5)

Т.к. в установке

, т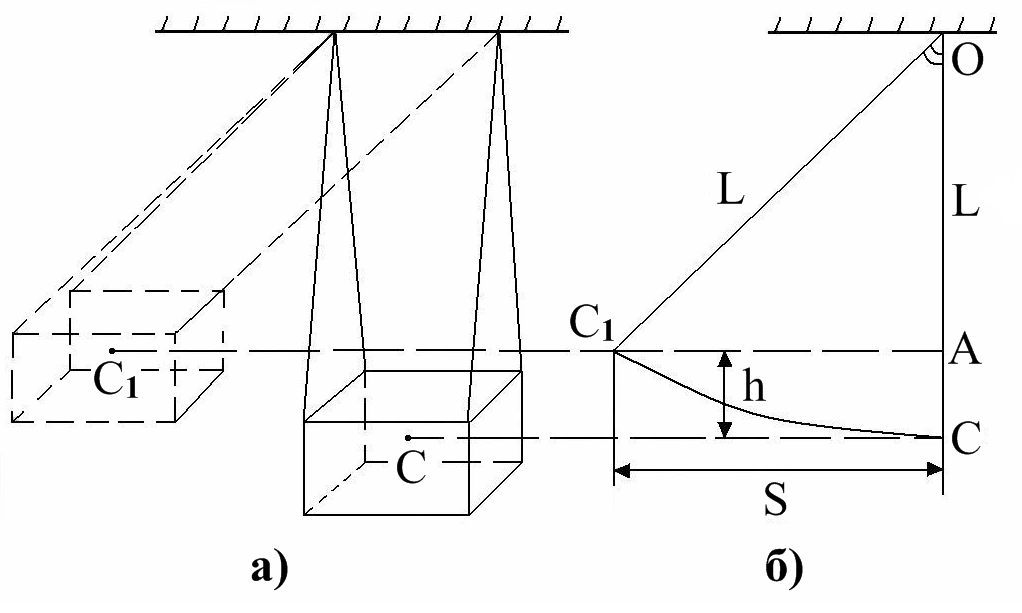о . (5.6)

С учетом (5.6) получим из (5.3) окончательное выражение для скорости пули:

, (5.7)

г
Рис. 5.2. Схема движения

баллистического маятника
де M и m – массы маятника и пули, L – высота подвеса центра тяжести маятника, S – максимальное горизонтальное смещение, вызванное неупругим ударом пули и маятника. Значения M и L указаны на маятнике.
Измерения и обработка результатов

1. 
   Составить таблицу для записи результатов измерений и вычислений. Определить взвешиванием массу пули.
   
2. 
   Привести установку в рабочее состояние, для чего: зарядить баллистический пистолет и установить маятник и пистолет так, чтобы ось пистолета совпадала с горизонтальной осью баллистического маятника (рис. 5.1).
   
3. 
   Произвести выстрел (пуля должна влететь в коробку маятника вдоль её оси) и определить смещение коробки по шкале 4 (рис. 5.1). Удар должен быть неупругим. Повторить опыт 5–6 раз, найти S_ср.
   
4. 
   Вычислить скорость пули по формуле (5.7).
   
5. 
   Оценить абсолютную (Δυ) и относительную (ε_υ) погрешности измерений, используя формулы:
   

, .

6. 
   Представить результат в следующем виде:
   

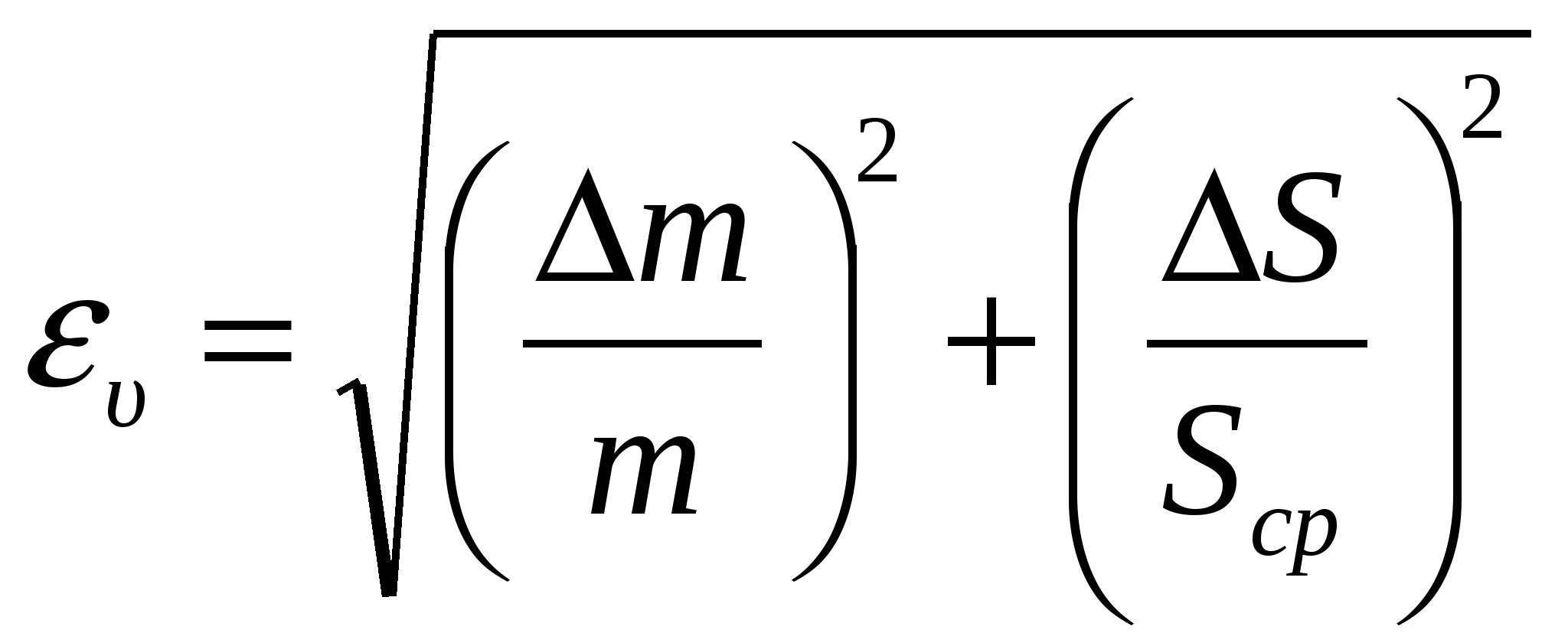υ = υ ± Δυ.
Контрольные вопросы

1. 
   Сформулируйте закон сохранения импульса. Какая система тел называется замкнутой?
   
2. 
   Какие силы называются консервативными, диссипативными? Сформулируйте закон сохранения механической энергии.
   
3. 
   Запишите эти законы для неупругого удара пули с маятником и для движущегося маятника (с пулей).
   
4. 
   Можно ли считать, что кинетическая энергия пули в случае неупругого удара полностью переходит в потенциальную энергию маятника? Ответ пояснить.
   
5. 
   Какой удар (упругий или неупругий) имеет место в следующих случаях:
   

1. 
   пуля застряла в бруске,
   
2. 
   мяч отскочил от стены,
   
3. 
   вратарь в прыжке поймал мяч,
   
4. 
   биллиардный шар ударил другой так, что оба влетели в две разные лузы.
   

6. 
   Выведите и разъясните рабочую формулу (5.7).
   

Лабораторная работа 6
ИЗУЧЕНИЕ СВОБОДНОГО ПАДЕНИЯ ТЕЛА
Цели работы: изучить зависимость перемещения от времени движения и представить её графически; определить ускорение свободного падения.

Приборы и принадлежности: установка для определения ускорения свободного падения.

Библиографический список: [1] § 23; [2] ч.1 § 12, § 15; [3] т.1 § 16, § 33; [6] т.1 § 23; [7] § 1.3.4.
Введение

Свободным падением называют движение в вакууме под действием только силы тяжести. Ускорение тела в этом случае называют ускорением свободного падения. По второму закону Ньютона:

, (6.1)

где F_T – сила тяжести тела массой m.

Траектория, перемещение и скорость при свободном падении зависят от начальной скорости υ₀. При υ₀ = 0 тело, находящееся на высоте Hи представленное самому себе, движется по вертикали. Тогда его перемещение (высота H) и конечная скорость υ равны:

, (6.2)

. (6.3)

В общем случае значение g зависит от высоты h над поверхностью Земли и широты φ местности. Ускорение свободного падения на полюсе (φ = π/2) максимально, а на экваторе (φ = 0) минимально:

, (6.4)

. (6.5)

Здесь M,R, ω –соответственно масса, радиус и угловая скорость вращения Земли.

Относительное изменение gпри переходе с полюса на экватор составляет примерно 0,3% от g_max. Вследствие сплюснутости Земли gизменяется дополнительно с широтой. В итоге ускорение свободного падения g изменяется от 9,730 м/с² (на экваторе) до 9,832 м/с² (на полюсе). Для Абакана (φ = 56°) g= 9,82 м/с². Значениеg= 9,81 м/с² принято за стандартное (табличное).
Описание экспериментальной установки

Установка для определения ускорения свободного падения (рис. 6.1) состоит из вертикальной штанги 1 с сантиметровой шкалой, счётчика-секундомера 2 и фотоэлектрического датчика 3, укрепленного на штативе.

Ш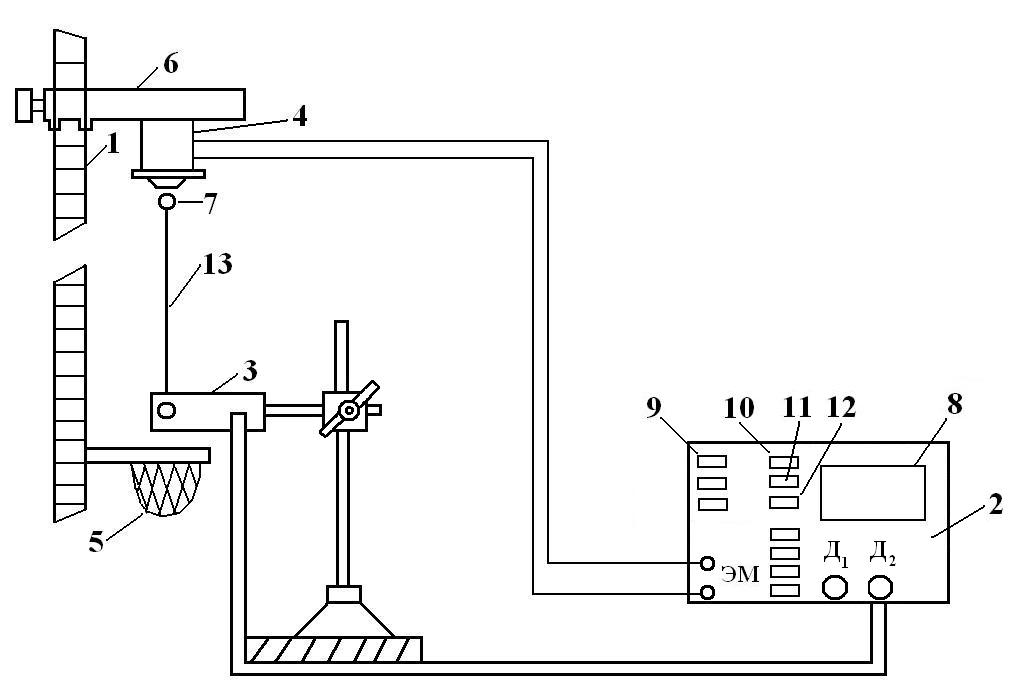
Рис. 6.1. Схема экспериментальной

установки
танга с помощью 2-х кронштейнов крепится к стене. К штанге прикреплены электромагнит 4 (для фиксации начального положения шарика 7) и шарикоприёмник 5. Электромагнит можно перемещать вдоль штанги с помощью кронштейна 6.

Взаимное расположение электромагнита 4 (его острия) и штатива с датчиком 3 должно быть таким, чтобы шарик 7 при падении пересёк луч датчика.

Счётчик-секундомер позволяет производить отсчёт времени с точностью 0,01с. На передней панели счётчика-секундомера расположены:

8 - информационное световое табло;

ЭМ - гнёзда для подключения электромагнита 4;

Д₂ - гнездо для подключения электромагнитного датчика 3;

9 - клавиша «СЕТЬ» (для подключения напряжения на фотоэлектрический датчик и электромагнит);

10. 
    - клавиша «ПУСК» (для обесточивания электромагнита);
    
11. 
    - клавиша «СТОП» (для прекращения отсчёта времени);
    
12. 
    - клавиша «СБРОС» (для обнуления светового табло).
    

Правила работы

с установкой для определения ускорения свободного падения

1. 
   Проверить работоспособность счётчика-секундомера:
   

1. 
   подключив к секундомеру электромагнит 4 и датчик 3, включить секундомер;
   
2. 
   нажать сначала на клавишу «СЕТЬ» (остальные клавиши должны быть в отжатом состоянии), а затем на клавишу «ПУСК» (при этом должен начаться отсчёт времени на табло 8);
   
3. 
   прервать луч датчика (отсчёт времени должен прекратиться);
   
4. 
   нажать на кнопку «СБРОС» (табло 8 должно вернуться в исходное состояние).
   

2. 
   Вращая кронштейн 6, и перемещая штатив с датчиком, добиться правильного расположения электромагнита 4 относительно датчика 3 (использовать отвес 13). При правильном положении электромагнита на нити отвеса виден световой зайчик. Затем отодвинуть отвес.
   
3. 
   Нажать на клавишу «СЕТЬ» и подвесить шарик 7 к электромагниту.
   
4. 
   Нажать на клавишу «ПУСК» и снять показания со светового табло 8 после прекращения отсчёта времени (причина последнего – пересечение светового луча датчика падающим шариком). Если шарик не прервёт луч необходимо нажать последовательно на клавиши «СТОП» и «СБРОС», а затем повторить пункт 2.
   
5. 
   Сняв показания отсчёта времени, нажать на клавишу «СБРОС» (вернув тем самым счётчик секундомер в исходное состояние).
   
6. 
   По окончании измерений все клавиши счётчика-секундомера должны быть в отжатом положении. Прибор отключить от сети.