Мех_нефиз_240_24.10.2011. Мех_нефиз_240_24.10. Учебнометодический комплекс по дисциплине для нефизических специальностей Лабораторный практикум Абакан 2011 ббк 22. 2я73

• Название: Учебнометодический комплекс по дисциплине для нефизических специальностей Лабораторный практикум Абакан 2011 ббк 22. 2я73
• Анкор: Мех_нефиз_240_24.10.2011.doc
• Дата: 09.05.2017
• Размер: 1.9 Mb.
• Имя файла: Мех_нефиз_240_24.10.2011.doc
• Тип: Учебно-методический комплекс; #7342
• страница: 4 из 12

Контрольные вопросы

1. 
   Сформулируйте закон всемирного тяготения. Дайте понятие ускорения свободного падения, используя этот закон.
   
2. 
   Что называется свободным падением тел? Отчего зависит ускорение свободного падения?
   
3. 
   Как изменится время падения тела, если экспериментальную установку перенести на высоту 100 км?
   
4. 
   Как изменится время падения, если опыт провести на полюсе (на экваторе)? Установку перенести на поверхность Луны? Почему?
   
5. 
   Опишите устройство и принцип действия установки для определения ускорения свободного падения.
   

Лабораторная работа 7
ИЗУЧЕНИЕ ДЕФОРМАЦИИ ИЗГИБА
Цели работы: получить зависимость прогиба от нагрузки и представить эту зависимость графически; вычислить модуль Юнга.

Приборы и принадлежности: Прибор ФП – 3А (для изучения деформации изгиба) с набором гирь; линейка метровая; штангенциркуль.

Библиографический список: [1] § 21; [2] ч.1 § 10, § 54; [3] т.1 § 14; [4] т.1 § 49; [5] § 6.1–6.3; [7] § 1.3.4.
Введение

Важным примером деформации твердого тела является изгиб стержня (рис. 7.1) под действием поперечных нагрузок (сил, приложенных перпендикулярно к оси стержня).

При такой деформации верхние слои стержня удлиняются, нижние сжимаются, а длина центрального слоя остается неизменной (ОО₁^/ = О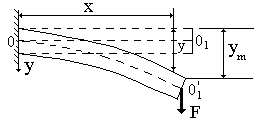О₁). Все поперечные сечения наклоняются в сторону изгиба и остаются плоскими.

О
Рис. 7.1.
тклонение (y) точки с координатой x от прямой, на которой лежала эта точка до деформации, называется прогибом, максимальный прогиб y_m – «стрелой» прогиба (рис 7.1).

В общем случае причиной изгиба стержня является действие двух сил: силы тяжести самого стержня и внешней силы.

Для упругого изгиба прогиб стержня при одновременном действии двух сил равен сумме прогибов, вызываемых каждой силой. Если за начальную точку отсчета взять положение точек стержня в отсутствие внешней силы, то можно говорить об изгибе, вызванном только внешней силой. Для такого случая прогиб точки зависит от:

1. 
   координаты x этой точки;
   
2. 
   материала стержня (его модуля Юнга Е)
   
3. 
   деформирующей силы F и её плеча l (или от изгибающего момента M = Fl).
   

Прогиб y равен:

, (7.1)

где А – коэффициент пропорциональности, зависящий от формы, поперечного сечения стержня и условий его закрепления.

Для точки с фиксированной координатой x из (7.1) получим закон Гука для изгиба (прогиб стержня пропорционален изгибающему моменту и обратно пропорционален модулю Юнга):

, (7.2)

здесь В=Ах². (7.3)

Описание экспериментальной установки

Прибор ФП – 3А представляет собой (рис. 7.2) раму 1, установленную в опорах 2. На раме находится стальной стержень 3 переменной ширины. Стержень закреплен с одной стороны неподвижно, а с другой (незакрепленной) стороны стержня имеется опорная призма с подвеской 4 для гирь (гири прилагаются к прибору).

К раме 1 винтовым прижимом 6 прикрепляется индикатор 5, с помощью которого измеряют изгиб стержня. Прижим имеет винты 7, 8 и 9 (рис 7.2а и 7.2б). Винт 7 закрепляет прижим 6 на раме, винтом 8 индикатор прикрепляется к винтовому прижиму, винт 9 позволяет перемещать индикатор вдоль измерительного стержня 10 индикатора. Индикатор и опорную призму с подвеской можно перемещать вдоль стержня 3.

В
Рис. 7.2. Схема экспериментальной установки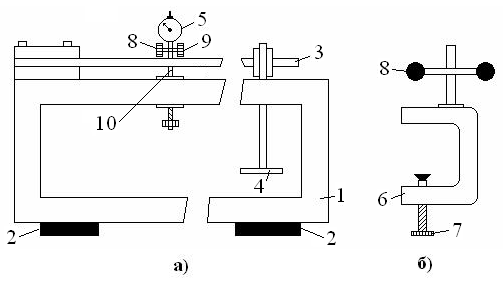
данной работе внешней силой является сила тяжести гирь (F=mg). Момент этой силы:

M = mgl, (7.5)

где l – плечо силы (расстояние от закрепленного конца до опорной призмы).

Е
Рис. 7.3. Стальной стержень

переменной ширины
сли середина опорной призмы лежит на риске cd, нанесенной на незакрепленном конце стержня (рис. 7.3), то коэффициент пропорциональности в формуле (7.1) равен:

, (7.6)

где а – ширина закрепленного конца стержня, b – толщина стержня.

Из уравнения (7.1) с учетом (7.5) и (7.6) получим формулу для прогиба стержня переменной ширины, закрепленного с одного конца:

, (7.7)

где . (7.8)

В работе необходимо проверить, согласно формуле (7.7), линейную зависимость прогиба y точки с фиксированной координатой xот деформирующей силы mg (проверить закон Гука) и вычислить модуль Юнга.

Измерения и обработка результатов

1. 
   Подготовить установку к работе. Для этого
   

1. 
   проверить отсутствие гирь на подвеске 4;
   
2. 
   установить индикатор 5 с помощью прижима 6 в заданном месте и подготовить его к началу измерений.
   

2. 
   С помощью линейки измерить длину l стержня 3. Используя штангенциркуль, определитьширину а закрепленного конца стержня и толщину b стержня.
   
3. 
   Измерить координату x (расстояние от закрепленного конца стержня до острия индикатора).
   
4. 
   Данные измерений занести в таблицу 7.1.
   

Таблица 7.1

a,	b,	l,	x,

5. 
   По формуле (7.8) вычислить коэффициент С.
   
6. 
   Получить зависимость прогиба y от деформирующей силы mg. Для этого установить «нуль» индикатора и измерить прогиб сначала при постепенной нагрузке подвески 4 гирями, а затем постепенной разгрузке её.
   
7. 
   Данные измерений занести в таблицу 7.2.
   

Таблица 7.2

№ опыта	1	2	2	4	и т.д.
F=mg, Н	1·9,8	2·9,8	3·9,8	4·9,8
y при нагрузке, мм
yпри разгрузке, мм
yср., мм

8. 
   По данным таблицы 7.2 построить график зависимости прогиба y_ср от силы F.
   
9. 
   Рассчитать модуль Юнга Е с помощью формулы (7.7) по наилучшей экспериментальной точке графика y_ср = f (F).
   
10. 
    Оценить абсолютную (ΔЕ) и относительную (ε_Е) погрешности измерений, используя формулы:
    

,

.

8. 
   Записать результат с учётом погрешности в следующем виде:
   

Е = Е ±ΔЕ.

9. 
   Сравнить полученное значение модуля Юнга Е с табличным значением для стали.