Мех_нефиз_240_24.10.2011. Мех_нефиз_240_24.10. Учебнометодический комплекс по дисциплине для нефизических специальностей Лабораторный практикум Абакан 2011 ббк 22. 2я73
 Скачать 1.9 Mb.
|
Контрольные вопросы
Лабораторная работа 8 ПРОВЕРКА ЗАКОНА СОХРАНЕНИЯ ИМПУЛЬСА Цели работы: проверить закон сохранения импульса для центрального упругого и неупругого ударов. Приборы и принадлежности: установка ФМ-17, выпрямитель, набор шаров, технические весы с разновесами. Библиографический список: [1] § 9, § 15; [2] ч.1 § 9, § 18; [3] т.1 § 8, §18, § 27-28; [4] т.1 § 4, § 8; [5] § 4.1, § 4.5; [7] § 1.4.1. Введение В 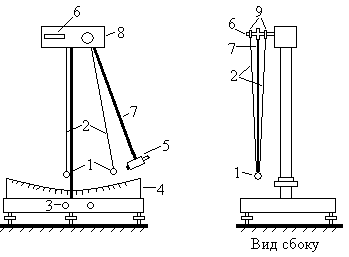 Рис. 8.1. Схема экспериментальной установки механике ударом называют кратковременное взаимодействие тел при их соприкосновении (столкновение шаров, попадание пули в мишень и т.д.). Соприкасающиеся тела деформируются. Если после удара деформация исчезает полностью, удар называют абсолютно упругим. В природе таких ударов не существует: всегда часть энергии затрачивается на необратимую деформацию. Однако в некоторых случаях (например: удар стальных шаров и т.д.) потерями механической энергии можно пренебречь и такие удары считаются абсолютно упругими. Удары, с которыми приходится иметь дело на практике, длятся тысячные и миллионные доли секунды. Поэтому можно пренебречь действием внешних сил за это время и применить закон сохранения импульса. Если скорости ударяющихся тел до и после взаимодействия направлены по прямой, проходящей через их центры масс, удар называют центральным и прямым. Ниже рассматриваются только такие удары. Теория метода и описание экспериментальной установки Экспериментальная установка ФМ – 17, используемая в данной работе (рис. 8.1) состоит из двух маятников – шаров 1 на бифилярных подвесах 2. Бифилярные подвесы укреплены на стержнях 6. Один из стержней с помощью ручки 3, выведенной на переднюю панель прибора перемещается вдоль панели 8. Шары при этом сближаются (или удаляются). Дуговая шкала 4 служит для отсчета угла отклонения шаров от положения равновесия. В правой части прибора укреплен электромагнит 5. Напряжение на электромагнит подается через выпрямитель. С помощью электромагнита можно удерживать шар в отклоненном положении. Если отклонить один из шаров и отпустить его, то вернувшись в положение равновесия, этот шар столкнется с неподвижным шаром. В соответствии с законом сохранения импульса имеем:
Здесь m2υ2 – проекция импульса правого шара до удара,  и  – проекции импульсов шаров после упругого удара,(m1 + m2)  – проекция импульсов шаров после неупругого удара.Все проекции определены относительно оси ОХ. С 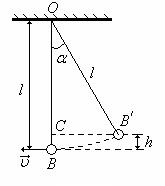 корость каждого шара (до и после удара) можно найти, используя закон сохранения энергии. Согласно этому закону, если пренебречь сопротивлением воздуха,  . (8.3) З Рис. 8.2. десь υ – скорость шара в момент прохождения положения равновесия, h – максимальная высота шара над положением равновесия. Из треугольника ОВ/С (рис. 8.2) следует: l – h = l cosα . (8.4) Используя уравнения (8.3) и (8.4), получим выражение для скорости:  , (8.5) где α – угол отклонения шара от положения равновесия, l – расстояние от точки подвеса до центра массы шара. В установке, используемой в лабораторной работе, угол α мал (меньше 8о), т.е. sin α ≈ α, тогда уравнение для скорости примет вид:  . (8.6)С учетом (8.6) уравнения (8.1) и (8.2) можно переписать в виде: Для упругого удара:  , (8.7)Для неупругого удара:  . (8.8)Здесь α2 – угол отклонения правого шара до удара (упругого или неупругого),  и  – углы отклонения шаров после упругого удара,  – угол отклонения обоих шаров после неупругого удара.В равенствах (8.7) и (8.8) нужно учитывать знаки углов (следствие учета знака проекции скоростей в (8.1) и (8.2) уравнениях). В данной работе проверить закон сохранения импульса – это проверить справедливость (8.7) и (8.8). Измерения и обработка результатов
При этом угол отклонения от положения равновесия каждого шара (как до, так и после удара) определяется как средняя величина из трёх измерений – трёх опытов. Для определения знака проекции скоростей (а, следовательно, углов отклонения шаров после удара) следить, чтобы удар был однократным. Данные измерений занести в таблицы 8.1 и 8.2. Таблица 8.1
Таблица 8.2
Для осуществления неупругого удара шаров одинаковой массы использовать пластилин (убрать его после окончания работы). Угол в уравнении (8.8) определять как угол отклонения линии, проходящей через точку касания шаров. Экспериментальные данные занести таблицу 8.3. Таблица 8.3
Сравнить левую и правую части уравнения (8.8), сделать вывод о справедливости закона сохранения импульса для неупругого удара. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
, (8.1)
. (8.2)