Мех_нефиз_240_24.10.2011. Мех_нефиз_240_24.10. Учебнометодический комплекс по дисциплине для нефизических специальностей Лабораторный практикум Абакан 2011 ббк 22. 2я73

• Название: Учебнометодический комплекс по дисциплине для нефизических специальностей Лабораторный практикум Абакан 2011 ббк 22. 2я73
• Анкор: Мех_нефиз_240_24.10.2011.doc
• Дата: 09.05.2017
• Размер: 1.9 Mb.
• Имя файла: Мех_нефиз_240_24.10.2011.doc
• Тип: Учебно-методический комплекс; #7342
• страница: 6 из 12

Контрольные вопросы

1. 
   Дать определение:
   
   1. 
      замкнутой системы,
      
   2. 
      импульса тела,
      
   3. 
      удара, упругого и неупругого ударов,
      
   4. 
      центрального прямого удара.
      
2. 
   Сформулировать закон сохранения импульса системы тел и дать его математическую запись.
   
3. 
   Получить уравнения (8.7) и (8.8).
   
4. 
   Какой удар (упругий или неупругий) имеет место в следующих случаях:
   

5. 
   пуля застряла в бруске,
   
6. 
   мяч отскочил от стены,
   
7. 
   вратарь в прыжке поймал мяч,
   
8. 
   биллиардный шар ударил другой так, что оба влетели в две разные лузы.
   

5. 
   Будет ли удар в последнем случае центральным?
   

ЦИКЛ 3. ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ.

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
Лабораторная работа 9
ИЗУЧЕНИЕ ОСНОВНОГО УРАВНЕНИЯ ДИНАМИКИ

ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ С ПОМОЩЬЮ МАЯТНИКА ОБЕРБЕКА
Цели работы: проверить зависимость углового ускорения от момента силы при постоянном моменте инерции и представить эту зависимость графически; определить момент инерции маятника Обербека.

Приборы и принадлежности: маятник Обербека, штангенциркуль, секундомер, набор грузов, технические весы с разновесом.

Библиографический список: [1] § 16–19; [2] ч.1 § 21–23; [3] т.1 § 38–39, § 41; [4] т.1 § 10 - 11; [5] § 2.10, § 5.1, § 5.3–5.4; § 5.11; [7] § 1.3.3.
Введение

В
Рис. 9.1.
ращательным движением абсолютно твердого тела называется движение, при котором все точки тела описывают окружности, лежащие в параллельных плоскостях, с центром, расположенным на прямой, называемой осью вращения.

Для описания вращательного движения вводят следующие величины: момент силы, момент инерции, момент импульса. Моментом силы относительно неподвижной точки О (рис. 9.1) называется векторная величина , равная векторному произведению радиус-вектора , проведенного из точки О в точку приложения силы, на вектор силы :

. (9.1)

Модуль вектора равен:

, (9.2)

где α – угол между направлениями векторов и , а d = r sin α – длина перпендикуляра, опущенного из точки О на прямую, вдоль которой действует сила (рис. 9.1). Эта длина называется плечом силы относительно точки О.

Моментом инерции I материальной точки относительно оси вращения называется физическая величина, равная произведению массы m точки на квадрат ее расстояния r до оси вращения:

I = m·r². (9.3)

Моментом инерции тела относительно неподвижной оси вращения называется сумма моментов инерции всех материальных точек, составляющих тело:

. (9.4)

Момент инерции характеризует инертные свойства вращающегося тела и зависит от распределения массы в теле, расположения оси вращения, формы тела.

Моментом импульса материальной точки относительно неподвижной точки О называется векторная величина , равная векторному произведению радиус-вектора на вектор импульса :

. (9.5)

Учитывая, что импульс материальной точки равен , получим еще одно выражение для момента импульса:

, (9.6)

где ω – угловая скорость материальной точки.

Основное уравнение динамики вращательного движения (или второй закон Ньютона для вращательного движения) в дифференциальной форме имеет вид:

, (9.7)

здесь – суммарный (результирующий) момент внешних сил относительно произвольного центра вращения О, – момент импульса твердого тела относительно этого же центра.

Если момент инерции тела относительно фиксированной оси вращения остается величиной постоянной, то уравнение (9.7) можно записать в виде:

, (9.8)

где М_z – проекция векторана ось вращения, проходящую через точку О (или момент силы относительно оси вращения), I_z – момент инерции относительно этой же оси, ε – угловое ускорение вращающегося тела.

Описание экспериментальной установки

В лабораторной работе проверяется справедливость основного уравнения динамики вращательного движения с помощью маятника Обербека.

М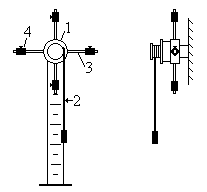аятник Обербека состоит (рис. 9.2) из ступенчатого шкива 1, укрепленного в центре крестовины. Крестовина со шкалой надета на ось. На одну из ступеней шкива наматывается нить 2, к концу которой можно подвесить груз массой m.

Н
Рис. 9.2. Маятник Обербека
а концах крестовины находятся грузы m^*. Их можно перемещать вдоль стержней 3 крестовины и закреплять на любом расстоянии от оси вращения с помощью винтов 4. При определенном расположении грузов m^* на стержнях центр тяжести маятника совпадает с осью вращения (маятник будет в безразличном равновесии). Таких состояний множество (если грузы на стержнях имеют одинаковую массу, то для безразличного равновесия маятника достаточно расположить эти грузы симметрично относительно оси вращения). Изменяя положение грузов m^*, можно изменять момент инерции маятника.

Маятник, находящийся в безразличном состоянии, приводится во вращение грузом m. Для такого маятника:

М_z = М_нат – М_тр , (9.9)

где М_нат – момент силы натяжения нити, М_тр – момент силы трения в оси маятника (его можно считать постоянным при вращении маятника в одну и ту же сторону).

Из (9.8) и (9.9) для маятника Обербека имеем:

. (9.10)

Угловое ускорение ε маятника и момент силы натяжения нити М_нат равны:

, (9.11)

, (9.12)

здесь h – высота падения груза за время t,D – диаметр шкива, а – линейное ускорение падения груза.

При а<<g формула (9.12) упрощается:

. (9.13)

Момент силы трения М_тр в работе определяется с помощью графика зависимости ε = f(М_нат).

В лабораторной работе проверяется справедливость уравнения (9.10). Формула (9.10) является линейной зависимостью между ε и М_нат, а ее график – прямой. Следовательно, если график, построенный по результатам измерений в координатах ε и М_нат, можно представить в виде прямой, то для маятника Обербека справедливо основное уравнение динамики вращательного движения и можно вычислить его момент инерции I_z.

Измерения и обработка результатов

Упражнение 1. Проверка зависимости углового ускорения маятника от момента силы при постоянном моменте инерции.

1. 
   Добиться безразличного равновесия маятника Обербека, т.е. при отклонении его из положения равновесия маятник должен оставаться в покое (грузы m^* на стержнях максимально удалены от оси вращения).
   
2. 
   Штангенциркулем измерить диаметр D шкива, на который наматывают нить (в трёх различных местах). Найти среднее значение D_ср.
   
3. 
   С помощью технических весов определить массу m трёх различных грузов.
   
4. 
   Измерить время падения t указанных трёх грузов с фиксированной высоты h. Время падения каждого груза измерить трижды. Найти среднее значение t_ср.
   
5. 
   Результаты всех измерений занести в таблицу 9.1:
   

Таблица 9.1

	m, кг	h, м	Dср, м	№ измер.	t, с	ε, с-2	Мнат, Н·м
1-й груз				1
				2
				3
				ср.
2-й груз				1
				2
				3
				ср.
3-й груз				1
				2
				3
				ср.

6. 
   По формулам (9.11) и (9.13) вычислить ε и М_нат, подставляя средние значения для каждой измеренной величины.
   
7. 
   По полученным данным построить график зависимости ε от М_нат.
   
8. 
   Сделать вывод о справедливости основного уравнения динамики вращательного движения.
   

Упражнение 2. Определение момента инерции маятника Обербека.

1. 
   Найти момент силы трения М_тр методом экстраполяции, т.е. продолжить экспериментальный график ε(М_нат), полученный в упражнении 1, до пересечения с осью М_нат, тогда М_тр = М_нат при ε= 0.
   
2. 
   По формуле (9.10) вычислить момент инерции маятника Обербека при различных моментах натяжения нити (при различных грузах m). Найти среднее значение I_ср.
   

Контрольные вопросы

1. 
   Какое движение называется вращательным? В чем отличие вращательного движения от поступательного?
   
2. 
   Что называется моментом силы относительно точки? В каких единицах он измеряется? Как определить его направление?
   
3. 
   Что называется моментом инерции тела, системы тел? Единицы измерения момента инерции?
   
4. 
   Каким образом можно изменить момент силы, момент инерции?
   
5. 
   Как записывается и формулируется второй закон Ньютона для вращательного движения?
   
6. 
   Как вы представляете себе безразличное равновесие маятника?
   
7. 
   Какие определения, формулы, законы используются при выводе формул (9.11) и (9.12)? Выведите их.
   

Лабораторная работа 10
ИЗУЧЕНИЕ СВОБОДНЫХ КОЛЕБАНИЙ

ПРУЖИННОГО МАЯТНИКА
Цель работы: ознакомление с характером свободных колебаний и определение их характеристик.

Приборы и принадлежности: пружинный маятник, секундомер.

Библиографический список: [1] § 140–142; [2] ч.1 § 27; [3] т.1 § 49, § 53–54; [4] т.1 § 50 - 51; [5] § 10.1–10.2; [7] § 3.1.1, § 3.2.1; [8] § 59–60, § 21.
Введение

Колебаниями называют движения или изменение состояния системы, отличающиеся той или иной повторяемостью во времени. Колебательные процессы могут существовать в объектах различной природы, в том числе в живых организмах, а также в системах различных размеров – от космических до молекулярных.

Колебания, при которых состояния системы повторяются через равные промежутки времени называют периодическими. Строго периодическими являются гармонические колебания, где изменение состояния системы со временем описывается при помощи периодической функции синуса (или косинуса). Для этих колебаний имеют определенный смысл и значения величины: амплитуда, период, частота, циклическая частота.

Период колебаний Т – это наименьший промежуток времени, через который повторяются определенные состояния системы. Или это время одного полного колебания. Единицы измерения [Т] = 1 с.

Частота ν – число колебаний в единицу времени (секунду). Единицы измерения [ν] = 1 Гц.

Циклическая (круговая) частота ω – число колебаний за 2π секунды. Единицы измерения [ω] = 1 с^-1.

Амплитуда X_m– наибольшее отклонение колеблющейся величины от состояния равновесия. Единицы измерения [X_m] = 1 м.

Существует классификация колебаний:

1. 
   Свободными (или собственными) колебаниями называются колебания, возникающие в системе, которая после выведения ее из состояния равновесия была предоставлена самой себе. Свободные колебания совершаются за счет первоначально сообщенной энергии системе извне при последующем отсутствии внешних воздействий.
   
2. 
   Вынужденные колебания – это колебания, совершающиеся под действием периодической внешней силы.
   
3. 
   Незатухающие колебания – это колебания, энергия которых не изменяется с течением времени. Свободные незатухающие колебания могут существовать только при отсутствии сил трения. Эти колебания являются гармоническими, их амплитуда не изменяется. В реальных системах могут возникать колебания, близкие к гармоническим, когда трение в системе сведено к минимуму.
   
4. 
   Свободные затухающие колебания – это колебания, энергия которых уменьшается с течением времени, следовательно, уменьшается их амплитуда. Причина – наличие сил трения в механических системах. Затухание нарушает периодичность колебаний.
   

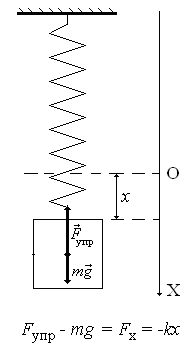
В
Рис. 10.1. Пружинный маятник
настоящей лабораторной работе изучаются свободные механические колебания на примере пружинного маятника.

Пружинный маятник – это груз массой m, подвешенный на упругой пружине жесткостью k (рис. 10.1). Если груз сместить из положения равновесия на отрезок х и предоставить самому себе, то пружинный маятник начнет колебаться. Это свободное колебание. При отсутствии сопротивления среды колебания будут незатухающими, при наличии сопротивления – колебания – затухающие.

Незатухающие свободные колебания пружинного маятника совершаются только под действием упругой силы (трение отсутствует). Ее проекция на ось Х по закону Гука (рис. 10.1):

F_x = – kx. (10.1)

Тогда основное уравнение движения маятника (второй закон Ньютона) в проекциях на ось X имеет вид:

F_x = ma_x или , (10.2)

где – ускорение.

Уравнение (10.2) является дифференциальным уравнением, которое принято записывать в стандартной форме:

или , (10.3)

здесь– собственная циклическая частота пружинного маятника.

Решением уравнения (10.3) является уравнение гармонических колебаний:

x = X_mcos(ω₀t + φ₀), (10.4)

где x – смещение маятника в момент времениt,ω₀t + φ₀ = φ – фаза колебаний в тот же момент времени,φ₀ – начальная фаза колебаний.

Период собственных колебаний пружинного маятника будет равен:

. (10.5)

Затухающие свободные колебания пружинного маятника совершаются под действием двух сил: упругой силы пружины F_x = – kx и силы сопротивления среды (направленной противоположно скорости):

, (10.6)

где r – коэффициент сопротивления, который зависит от свойств среды (вязкости), а также от размеров и формы груза и пружины;

– скорость движения.

Теперь основное уравнение движения маятника (уравнение затухающих колебаний) в проекциях на ось X имеет вид:

или . (10.7)

Если силы сопротивления не велики и r/m<< ω₀, колебания маятника будут слабо затухающими и решение уравнения (10.7) будет иметь вид:

(10.8)

– это уравнение (закон) затухающих колебаний. Выражение:

(10.9)

– закон изменения амплитуды с течением времени. Здесь X_m – амплитуда колебаний в момент времени t, – начальная амплитуда (t = 0), – коэффициент затухания. Очевидно, что слабо затухающие колебания не являются строго периодическими: амплитуда монотонно убывает по экспоненциальному закону (10.9). Величина ω – циклическая частота затухающих колебаний, которая равна:

. (10.10)

Период затухающих колебаний пружинного маятника будет равен:

. (10.11)

Из формулы (10.10) видно, что в случае затухающих колебаний ω₀ > ω, тогда согласно (10.5) и (10.11) должно выполняться неравенство:

T₀ < Т, (10.12)

которое проверяется в настоящей лабораторной работе.
Описание экспериментальной установки

В лабораторной работе изучаются свободные механические колебания пружинного маятника с небольшим затуханием. Определяется жесткость пружины и справедливость соотношения (10.12).

Лабораторный прибор собран на штативе 1 с вертикальной стойкой, снабженной сантиметровой шкалой 2 (рис. 10.2). В верхней части стойки укреплен пружинный маятник. Он представляет собой цилиндрическую спиральную пружину 3 с подвешенным к нему грузом 4. Для увеличения сопротивления воздуха (для усиления затухания колебаний) над грузом укреплен легкий диск 5, который одновременно служит указателем положения маятника относительно вертикальной шкалы.

С
Рис. 10.2. Лабораторная установка
пружиной следует обращаться бережно. Начальное смещение груза не должно превышать 10 см. После проведения измерений груз снимают и помещают в коробку на основании прибора. Это обеспечит сохранение неизменными свойств пружины, ее жесткости.

Под действием подвешенного груза пружина маятника деформируется – удлиняется на величину , где x₁ – положение конца пружины (диска) без груза, x₂ – с грузом. В соответствии с законом Гука жесткость пружины равна:

, (10.13)

здесь F – упругая сила, равная по модулю внешней деформирующей силе, т.е. весу груза P = m_грg, m_гр – масса груза, которая указана на лабораторной установке, g = 9,81 м/с² – ускорение свободного падения.

Период Т₀ собственных колебаний пружинного маятника определяется по формуле (10.5), в которую необходимо подставить массу маятника – m (суммарную массу груза и его подвеса с диском). Она также указана на приборе.

Период Т затухающих колебаний можно найти исходя из определения периода по формуле:

, (10.14)

где t – время, за которое маятник совершает n полных колебаний.

Измерения и обработка результатов

Упражнение 1. Определение жесткости пружины.

1. 
   По сантиметровой шкале определить положение пружины (диска) без груза – x₁ и с грузом – x₂.
   
2. 
   Результаты измерений и вычислений занести в таблицу 10.1.
   

Таблица 10.1

mгр, 10-3 кг	x1, 10-2 м	x2, 10-2 м	, 10-2 м	k, Н/м

3. 
   По формуле (10.13) вычислить жесткость пружины k.
   
4. 
   Вычислить относительную и абсолютную погрешности измерений k по формулам:
   

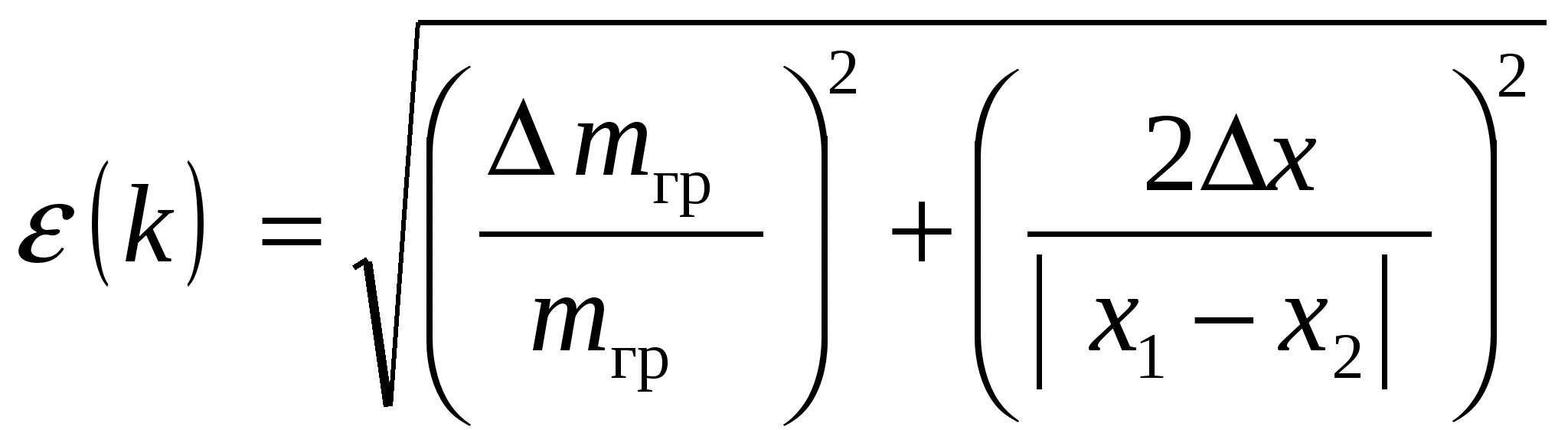, ∆k = ε(k) · k,

где ∆m_гр = 0,5 г; ∆x = ∆x₁ = ∆x₂ = 0,5 см.

5. 
   Результат представить в виде:
   

k = k ± ∆k_.
Упражнение 2. Определение периода собственных колебаний пружинного маятника.

1. 
   Рассчитать период Т₀ собственных колебаний пружинного маятника по формуле (10.5), используя данные для k и m (масса маятника указана на приборе).
   
2. 
   Вычислить относительную и абсолютную погрешности измерений Т₀ по формулам:
   

, ∆ Т₀ = ε(Т₀) · Т₀ ,

где ∆m = 0,5 г.

3. 
   Результат представить в виде:
   

Т₀ = Т₀ ± ∆Т₀.
Упражнение 3. Определение периода затухающих колебаний пружинного маятника.

1. 
   Используя секундомер, измерить время t, за которое маятник совершает n (n ≥ 10) полных колебаний. Опыт повторить три раза.
   
2. 
   По формуле (10.14) вычислить период Т колебаний пружинного маятника.
   
3. 
   По результатам трех измерений определить среднее значение периода Т_ср колебаний и среднеарифметическую погрешность ΔТ его измерения:
   

,

здесь индекс i соответствует номеру измерения, а n – общее число измерений.

4. 
   Данные измерений и вычислений занести в таблицу 10.2.
   

Таблица 10.2

№ п/п	n	t, с	Т, с	Тср, с	ΔТ, с
1
2
3

5. 
   Результат представить в виде:
   

Т = Т_ср ± ∆ Т.

6. 
   Сравнить значения периодов Т₀ и Т, полученные в двух упражнениях. Сделать вывод о степени затухания колебаний лабораторного маятника.
   

Контрольные вопросы

1. 
   Что называют колебаниями? Примеры колебаний различной природы, в том числе в биологических объектах и в тепловом движении сложных молекул.
   
2. 
   Запишите второй закон Ньютона для незатухающих и затухающих колебаний пружинного маятника.
   
3. 
   Какие колебания называют гармоническими? Закон смещения для гармонических колебаний, график зависимости.
   
4. 
   Дайте определение и запишите формулы для: периода, частоты, циклической частоты, амплитуды и фазы колебаний.
   
5. 
   Какие колебания маятника называют свободными затухающими? Как выглядит их график и закон изменения амплитуды?
   
6. 
   В каком случае выполняется неравенство: T₀ < Т?
   

Лабораторная работа 11
ИЗУЧЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ
Цели работы: получить зависимость амплитуды затухающих колебаний от числа колебаний и представить эту зависимость графически; вычислить величины, характеризующие колебания.

Приборы и принадлежности: установка для измерения амплитуды затухающих колебаний, секундомер.

Библиографический список: [1] § 142, §146; [2] ч.1 § 27, § 31; [3] § 49, § 53–54, § 58; [4] § 50 – 51, § 54; [5] § 10.1–10.2; [7] § 3.1.1, § 3.1.3, § 3.2.1.
Введение

Совокупность связанных между собой тел, способных совершать колебания, называют колебательной системой. Простейшей колебательной системой является пружинный маятник – это груз массой m, подвешенный на упругой пружине. Различные пружинные маятники отличаются друг от друга массой груза и коэффициентом жесткости (или упругости) пружины k.

Рассмотрим пружинный маятник сосредоточенной массы (масса маятника приблизительно равна массе подвешенного груза). В состоянии равновесия сила тяжести груза уравновешивается силой упругости (рис. 11.1б) и второй закон Ньютона в проекции на ось Х будет иметь вид:

mg – kΔl = 0 (11.1)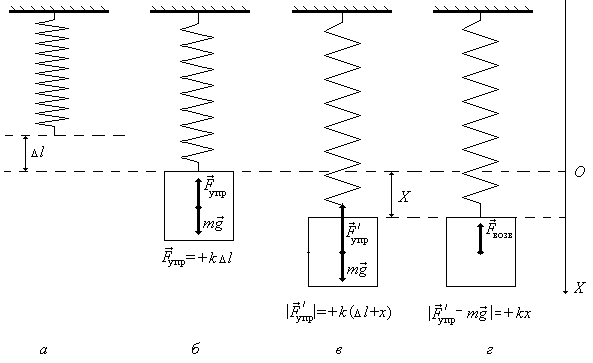

Рис. 11.1. Пружинный маятник


Если груз сместить из положения равновесия на отрезок х (рис. 11.1в) и предоставить самому себе, то пружинный маятник начнет совершать колебания. Такие колебания называют свободными. В отсутствии сопротивления среды колебания будут незатухающими, при наличии сопротивления – колебания – затухающие. Уравнение движения (2-й закон Ньютона) для затухающих колебаний имеет вид:

(11.2)

или с учетом (11.1)

. (11.3)

Здесь – kx – так называемая, возвращающая сила F_возв. (рис. 11.1в,г),

– сила сопротивления при малых скоростях движения,

r– коэффициент сопротивления.

Решением уравнения (11.3) будет функция

, (11.4)

где , (11.5)

. (11.6)

Коэффициент β, характеризующий быстроту затухания во времени, называется коэффициентом затухания.

Согласно (11.4), затухающие колебания можно считать гармоническими колебаниями частоты ω и переменной амплитудой, равной

(1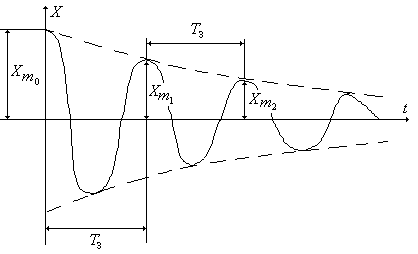1.7)

На рисунке 11.2 приведен график зависимости смещения маятника от времени в случае затухающих колебаний. Пунктирные линии на графике дают предельные значения максимального смещения (амплитуды) затухающих колебаний; – амплитуда в начальный момент времени; Т_з – период затухающих колебаний:


Рис. 11.2.
, (11.8)

здесь t – время, за которое маятник совершает n полных колебаний.

Быстрота затухания, помимо коэффициента затухания β, характеризуется логарифмическим декрементом D, временем релаксации τ и добротностью Q.

Логарифмический декремент – это натуральный логарифм отношения двух последовательных амплитуд (крайних отклонений в одну сторону через период Т_з (рис. 11.2)).

. (11.9)

Учитывая (11.7) уравнение (11.9) можно записать в виде:

. (11.10)

Время релаксации τ – это время, в течение которого амплитуда колебаний уменьшается в е раз (условно принято считать, что за это время колебания прекращаются). Согласно этому определению из (11.7) получим:

. (11.11)

Тогда равнение (11.10) можно представить в виде:

, (11.12)

где N_τ – число колебаний за время τ (такое число колебаний совершит система, прежде чем её амплитуда уменьшится в е раз).

Добротность колебательной системы определяется формулой:

. (11.13)

Можно показать, что при слабых затуханиях добротность пропорциональна отношению полного запаса энергии колебательной системы W(t) к энергии, теряемой за период:

. (11.14)
При экспериментальном исследовании затухающих колебаний необходимо проверить, соответствуют ли экспериментальные результаты для зависимости X_mотt выражению (11.7). Для этого прологарифмируем уравнение (11.7) и, учтя (11.9), получим:

, (11.15)

Из выражения (11.5) следует вывод: согласно теории, натуральный логарифм амплитуды затухающих колебаний линейно зависит от числа колебаний. Таким образом, убедиться в том, что экспериментальные результаты соответствуют (или не соответствуют) теории, можно, построив график зависимости lnX_m от n.
Описание экспериментальной установки

У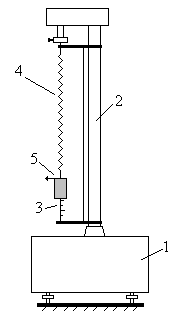становка, используемая в работе, состоит из подставки 1 с вертикальной стойкой 2, снабженной сантиметровой шкалой 3 (рис. 11.3). В верхней части стойки укреплен пружинный маятник. Он представляет собой цилиндрическую спиральную пружину 4 с подвешенным к ней грузом, на который укреплен визир 5.

Масса груза m подбирается такой, чтобы, во-первых, деформация пружины была упругой, во-вторых, чтобы масса груза не менее чем в 10 раз превышала массу пружины.

Измерения временных интервалов производятся с помощью секундомера.

Е
Рис. 11.3. Лабораторная установка
сли начальная амплитуда такова, что деформация пружины будет упругой, то можно использовать теорию затухающих колебаний, рассмотренную выше.

Измерения и обработка результатов

Упражнение 1. Проверка справедливости уравнения затухающих колебаний.

1. 
   Измерить амплитуды колебаний груза (крайнее отклонение в одну сторону) через определенное число n колебаний (это число и начальную амплитуду задает преподаватель).
   
2. 
   Вычислить натуральный логарифм начальной и последующих (измеренных) амплитуд.
   
3. 
   Данные измерений и вычислений занести в таблицу 11.1.
   

Таблица 11.1

n
Xm , см
ln Xm

4. 
   По полученным данным построить график зависимости натурального логарифма амплитуды ln X_m от числа колебаний n.
   
5. 
   Сделать вывод о справедливости уравнения затухающих колебаний (11.15).
   

Упражнение 2. Определение характеристик затухающих колебаний.

1. 
   Используя секундомер, измерить время t, за которое маятник совершает nполных колебаний (задает преподаватель). Вычислить период затухающих колебаний по формуле (11.8).
   
2. 
   Используя график зависимости lnX_m = f(n) и формулу (11.15) найти логарифмический декремент затухания.
   
3. 
   Вычислить коэффициент сопротивления r (масса груза написана на экспериментальной установке), коэффициент затухания β, время релаксации τ и добротность Q по формулам (11.5), (11.10), (11.11) и (11.13).