Мех_нефиз_240_24.10.2011. Мех_нефиз_240_24.10. Учебнометодический комплекс по дисциплине для нефизических специальностей Лабораторный практикум Абакан 2011 ббк 22. 2я73
 Скачать 1.9 Mb. Скачать 1.9 Mb.
|
Контрольные вопросы
Лабораторная работа 13 ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МЕТОДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ Цели работы: 1. Определить момент инерции исследуемого тела относительно двух осей:
2. Проверить теорему Штейнера. Приборы и принадлежности: трифилярный подвес, секундомер, метровая линейка, штангенциркуль, два цилиндрических тела. Библиографический список: [1] § 16–17; [2] ч.1 § 21–23; [3] т.1 § 38–39, § 41–42; [4] т.1 § 10 - 11; [5] § 2.10, § 5.1, § 5.3–5.4; [7] § 1.3.3. Введение2 Момент инерции – это физическая величина, являющаяся количественной мерой инертности вращающегося тела. Момент инерции твердого тела относительно какой-то оси вращения равен: где dm – масса бесконечно малого элементарного объёма тела, r– расстояние от оси вращения до этого объёма. Интеграл в формуле (13.1) берется по всему объёму тела V. Согласно формуле (13.1) момент инерции – величина аддитивная. Это означает, что момент инерции тела (системы тел) равен сумме моментов инерции составляющих частей. В общем случае нахождение момента инерции по формуле (13.1) представляет большие трудности. Задача упрощается, если ось вращения проходит через центр массы тела (ось симметрии). Зная момент инерции такого тела легко вычислить его момент инерции относительно любой другой оси, параллельной оси симметрии, используя теорему Штейнера. Согласно этой теореме, момент инерции тела I относительно произвольной оси равен моменту инерции Iс относительно оси, параллельной данной и проходящей через центр массы тела, плюс произведение массы тела m на квадрат расстояния между осями а: I = Ic + mа2. (13.2) Крутильным гармоническим колебанием называется периодическое движение около оси, проходящей через центр массы тела, при котором угол отклонения от положения равновесия изменяется по закону синуса или косинуса: где φm и Т – амплитуда и период крутильных колебаний. Теория метода и описание экспериментальной установки М 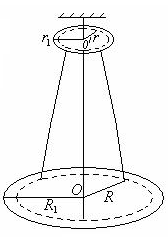 оменты инерции различных тел можно измерить методом крутильных колебаний с помощью трифилярного подвеса. Это однородный диск массой m и радиуса R1, подвешенный на 3-х симметрично расположенных нитях. Наверху эти нити симметрично закреплены на диске меньшего радиуса r1 (рис.13.1). оменты инерции различных тел можно измерить методом крутильных колебаний с помощью трифилярного подвеса. Это однородный диск массой m и радиуса R1, подвешенный на 3-х симметрично расположенных нитях. Наверху эти нити симметрично закреплены на диске меньшего радиуса r1 (рис.13.1).Т Рис. 13.1. Трифилярный подвес олчком к крутильным колебаниям служит небольшой вращательный импульс, сообщаемый нижнему или верхнему диску так, чтобы некрутильные колебания отсутствовали. При крутильных колебаниях центр тяжести нижнего диска поднимается по оси вращения на высоту h (рис. 13.2) и вновь возвращается в исходное положение. При отсутствии трения по закону сохранения энергии имеем: здесьm иI – масса и момент инерции нижнего диска (пустого), ωm – наибольшая угловая скорость при прохождении положения равновесия. Для гармонических крутильных колебаний: отсюда Теперь уравнение (13.4) можно представить в виде: В Рис. 13.2. ысоту h можно найти из геометрических построений. Из рис. 13.2: Так как φm – небольшой угол (гармонические колебания), то h 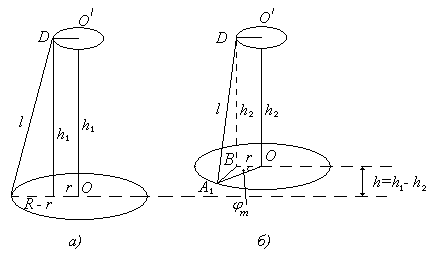 1 + h2 ≈ 2l, (13.9) где l– длина нити А1D. Используя рис. 13.2а и 13.2б определим h1 и h2: где R и r – радиусы окружностей крепления нитей на нижнем и верхнем дисках (рис. 13.1). Найдем отрезок А1В из треугольника Δ А1ВО (рис. 13.2б): А1В2 = R2 + r2 – 2Rr∙ cos φm. (13.12) Полученное выражение подставим в уравнение (13.11), тогда: С учетом (13.9), (13.10), (13.13) формула (13.7) для малых φm примет вид: Выразим из уравнения (13.7) момент инерции Iнижнего диска и подставим в полученное выражение формулу (13.10) для высоты h: или где m – масса нижнего диска (указана на диске), t– время n полных крутильных колебаний, D и d – диаметры окружностей крепления нитей на дисках (нижнем и верхнем), А – постоянная для данного трифилярного подвеса, которая рассчитывается по формуле: Если на нижний диск поместить исследуемое тело, то изменится масса, момент инерции и период колебаний системы диск-тело, однако формула (13.16) останется справедливой с учетом происшедших изменений. Таким образом, используя формулу (13.16) можно определить момент инерции пустого диска и диска с телом, а, следовательно, и момент инерции исследуемого тела. Измерения и обработка результатов
Таблица 13.1
Для каждого случая опыт повторить при одинаковых условиях 3 раза.
Таблица 13.1
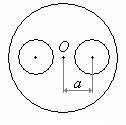
Iт = I2 – I1;
| ||||||||||||||||||||||||||||||||||||||||||
