|
|
Мех_нефиз_240_24.10.2011. Мех_нефиз_240_24.10. Учебнометодический комплекс по дисциплине для нефизических специальностей Лабораторный практикум Абакан 2011 ббк 22. 2я73
Контрольные вопросы
Какой маятник называется пружинным?
Какие колебания называются затухающими?
Запишите и разъясните уравнение движения для затухающих колебаний пружинного маятника.
Запишите и разъясните уравнение зависимости амплитуды затухающих колебаний от времени.
Изобразите графики зависимостей x(t), Xm(t) и lnXm(t) для случая затухающих колебаний.
Дайте определение логарифмического декремента затухания.
Дайте определение времени релаксации и добротности. Единицы их измерения.
Лабораторная работа 12
ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ
С ПОМОЩЬЮ МАТЕМАТИЧЕСКОГО МАЯТНИКА
Цели работы: получить из маятника данной конструкции математический маятник и определить ускорение свободного падения с помощью математического маятника.
Приборы и принадлежности: установка для определения ускорения свободного падения, выпрямитель, ключ, секундомер.
Библиографический список: [1] § 140–142; ; [2] ч.1 § 27, § 30; [3] т.1 § 49, § 53–54; [4] т.1 § 50 – 51; [5] § 10.1; [7] § 3.1.1, § 3.2.2.
Введение1
Математический маятник – это модель, которая представляет собой материальную точку, подвешенную на невесомой и нерастяжимой нити.
Математическим маятником приближенно можно считать тело, подвешенное на тонкой мало деформируемой нити длиной, намного превышающей размеры тела.
Е
Рис. 12.1.
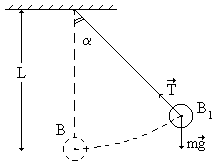 сли маятник отклонить (рис. 12.1) от положения равновесия (В) на угол α, а затем предоставить самому себе, он будет совершать колебательное движение около положения равновесия. Это свободные колебания. В отсутствие трения свободные колебания вызываются равнодействующей двух сил: силы тяжести сли маятник отклонить (рис. 12.1) от положения равновесия (В) на угол α, а затем предоставить самому себе, он будет совершать колебательное движение около положения равновесия. Это свободные колебания. В отсутствие трения свободные колебания вызываются равнодействующей двух сил: силы тяжести 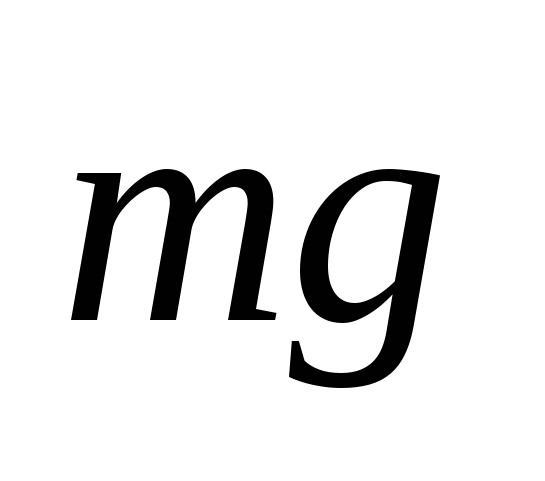 и силы натяжения и силы натяжения 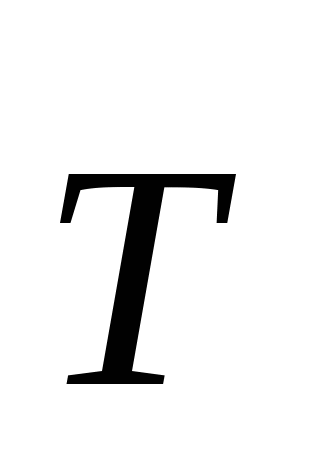 (рис. 12.1). Такие свободные колебания называются собственными. (рис. 12.1). Такие свободные колебания называются собственными.
При малых углах отклонения (α ≈ sinα ≈ tgα) собственные колебания будут гармоническими:
l = lmcos(ωot + φo) (12.1)
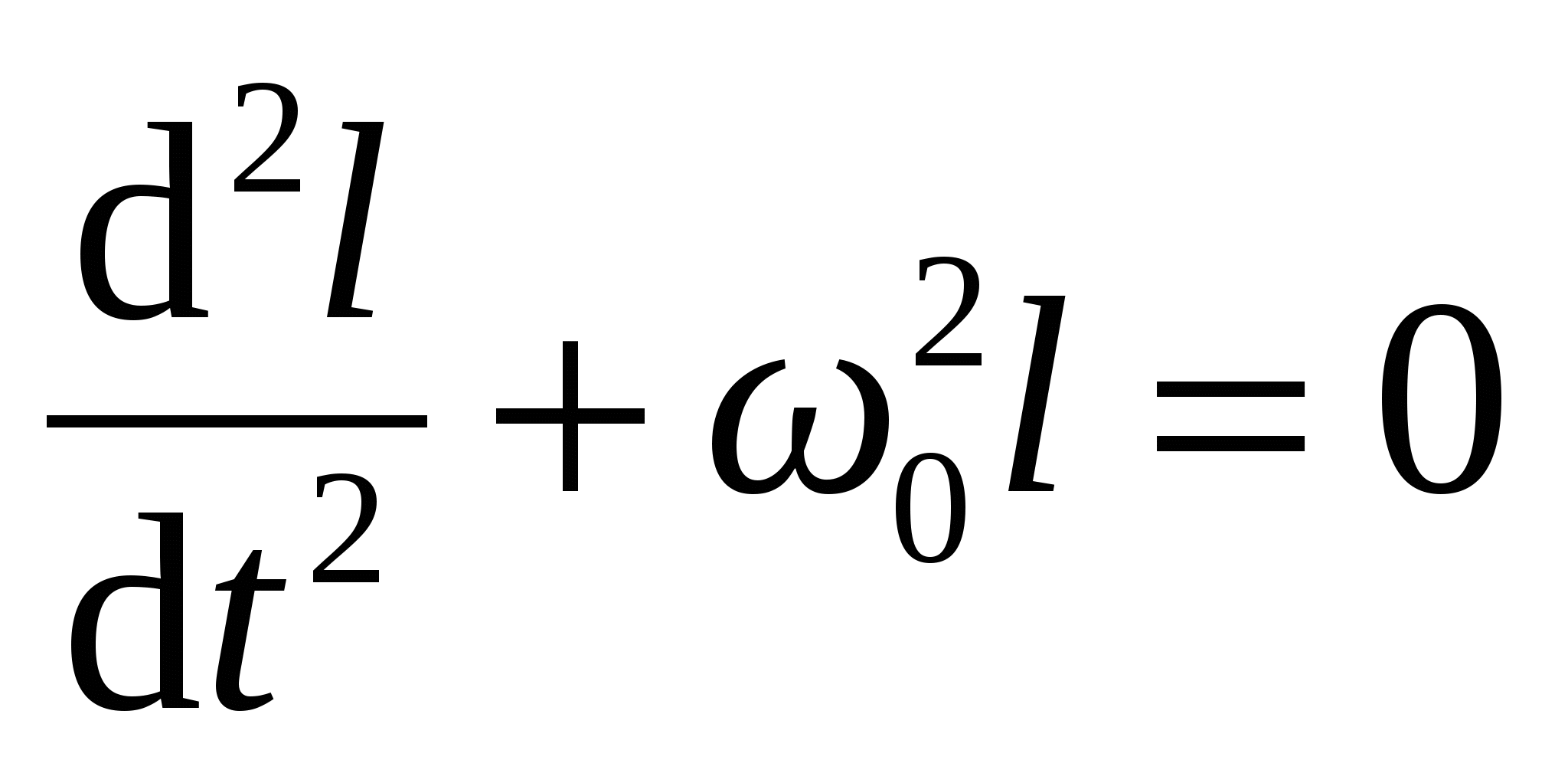 , (12.2) , (12.2)
где 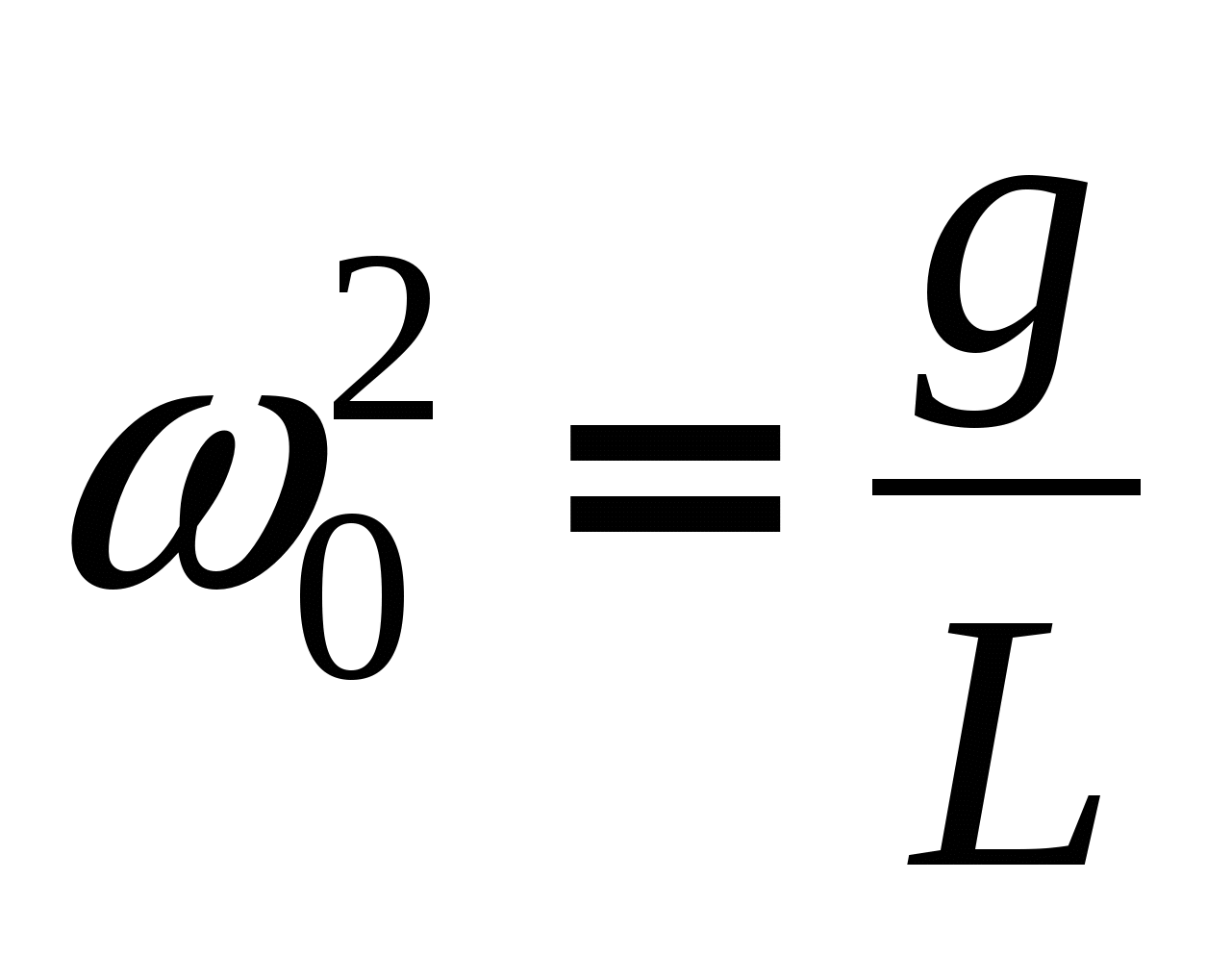 (12.3) (12.3)
В уравнениях (12.1), (12.2) и (12.3) l – дуговое смещение от положения равновесия, lm – амплитуда, L – длина маятника, ω0 – циклическая частота.
Период такого маятника
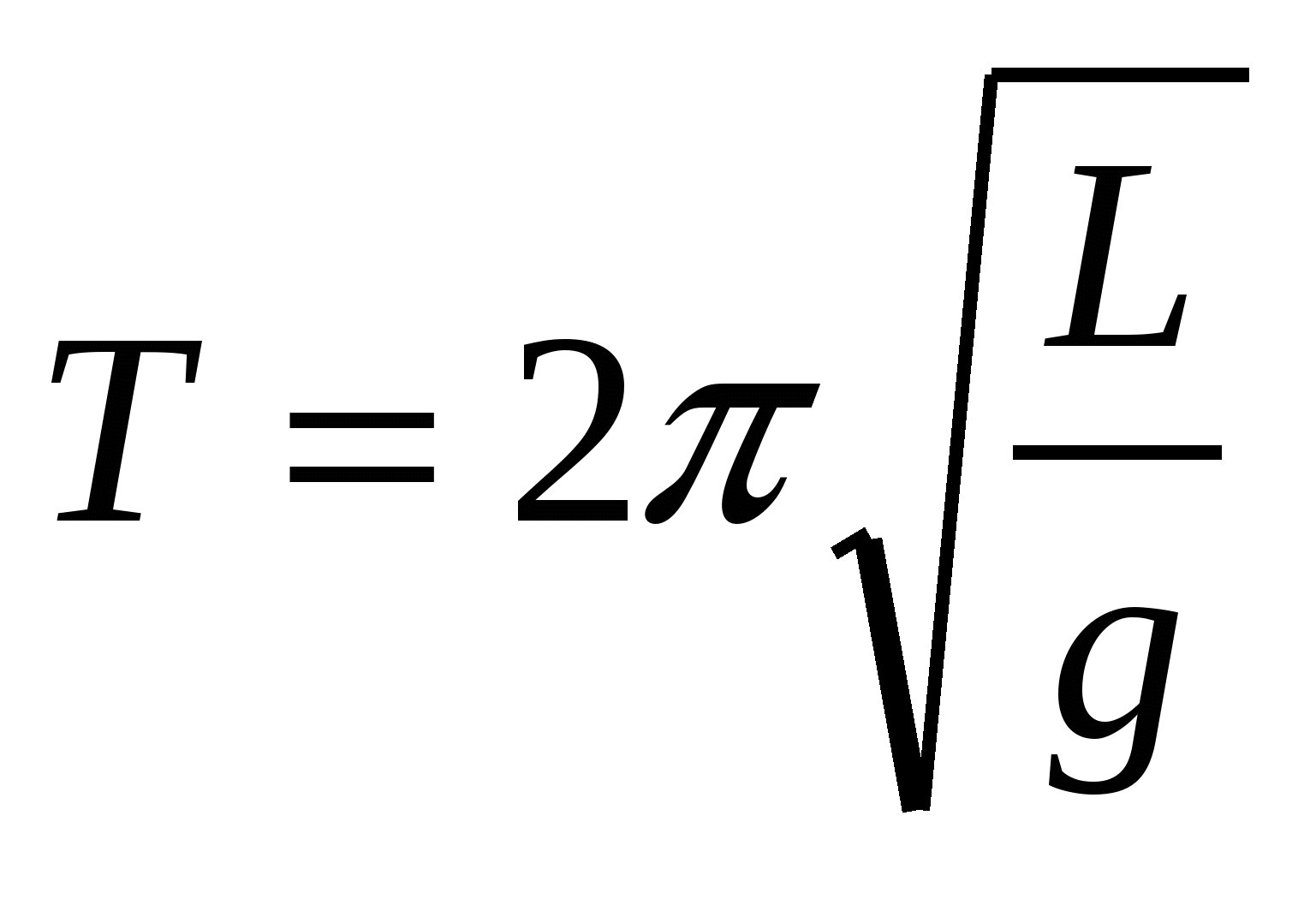 . (12.4) . (12.4)
Если положение центра тяжести в математическом маятнике точно не известно, для определения ускорения свободного падения используют математический маятник переменной длины. Для двух длин такого маятника имеем из (12.4):
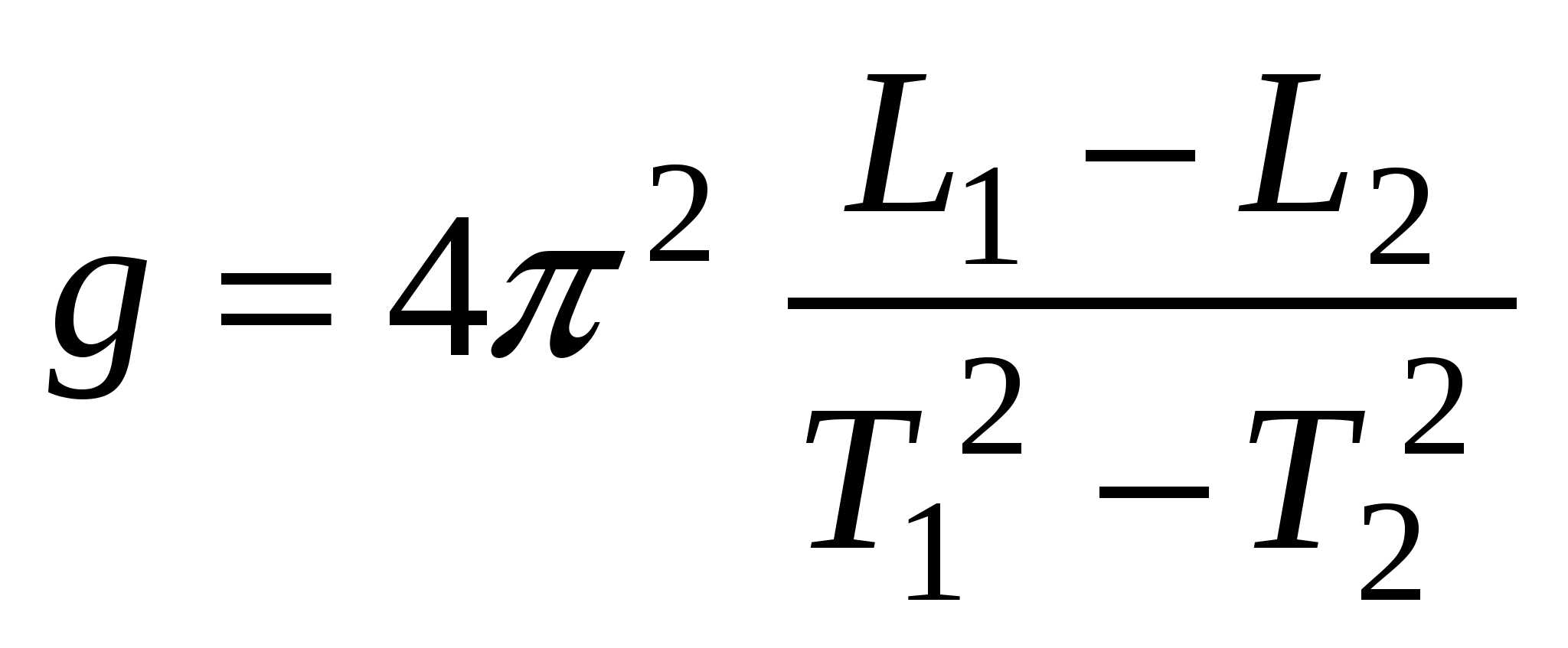 . (12.5) . (12.5)
Период колебаний математического маятника определяют экспериментально по формуле:
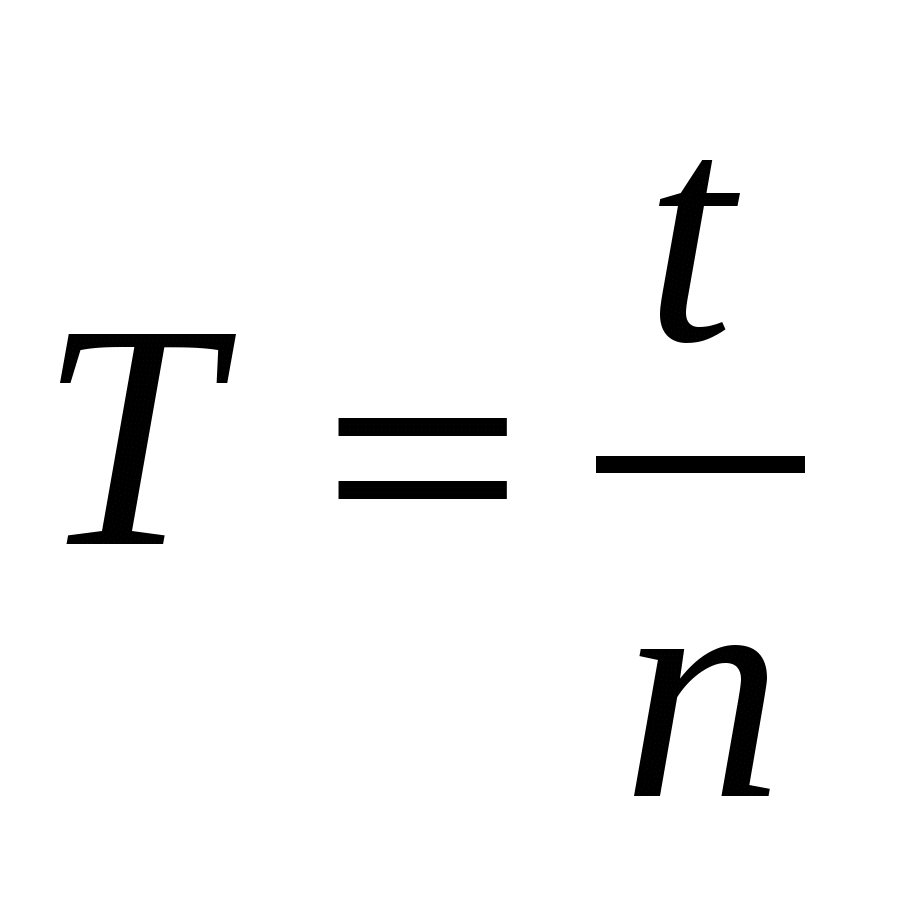 , (12.6) , (12.6)
где n – число колебаний за время t.
Если число колебаний взять одинаковым, из (12.5) и (12.6) получим:
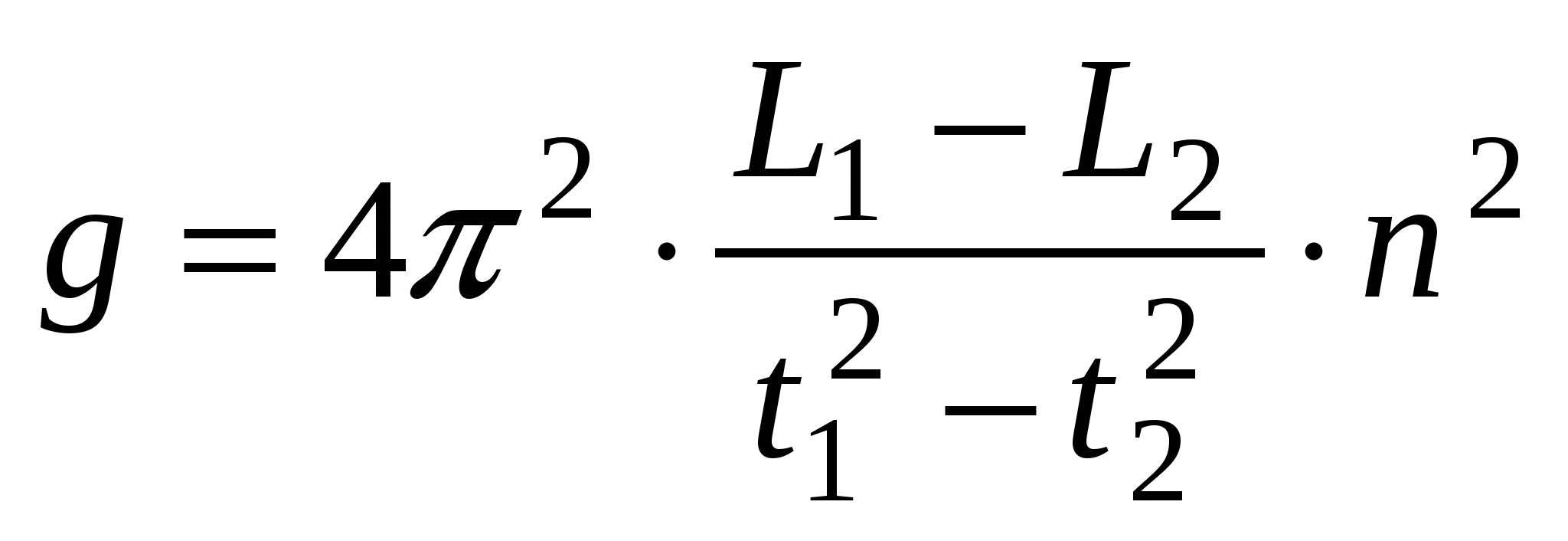 , (12.7) , (12.7)
здесь t1 и t2 – время колебаний маятников длиной L1 и L2, L1 - L2 – изменение длины математического маятника. Для определения L1 - L2 достаточно проследить за изменением положения любой точки маятника.
Описание экспериментальной установки
М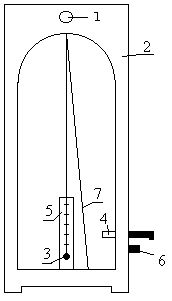 атематический маятник, используемый в этой работе – это тяжелый металлический шарик 3, подвешенный на нити (см. рис. 12.2). Маятник вмонтирован в деревянный корпус 2 со стеклянной дверкой. Длину нити можно измерять с помощью ручки 1. На задней стенке корпуса находится зеркало 5 со шкалой для отсчета изменения длины маятника и металлическая нить 7, фиксирующая максимальный угол отклонения маятника от положения равновесия. атематический маятник, используемый в этой работе – это тяжелый металлический шарик 3, подвешенный на нити (см. рис. 12.2). Маятник вмонтирован в деревянный корпус 2 со стеклянной дверкой. Длину нити можно измерять с помощью ручки 1. На задней стенке корпуса находится зеркало 5 со шкалой для отсчета изменения длины маятника и металлическая нить 7, фиксирующая максимальный угол отклонения маятника от положения равновесия.
В правую стенку корпуса вмонтирован электромагнит 4, который может перемещаться по вертикали и горизонтали и закрепляться в нужном положении винтом 6. На этой же стенке имеются клеммы питания электромагнита (на рис. 12.2 клеммы не указаны).
С
Рис. 12.2. Схема лабораторной установки
помощью электромагнита шарик отклоняется от положения равновесия. Для этого электромагнит, переместив по вертикали, закрепляют на нужной высоте винтом 6. Затем, вдвигая стержень электромагнита внутрь корпуса 2, сближают с шариком 3. Включив питание электромагнита, отклоняют шарик 3 от положения равновесия на необходимый угол, затем отключают питание электромагнита.
При правильной установке электромагнита (стержень электромагнита параллелен задней стенке корпуса 2), шарик 3 будет колебаться в этой же плоскости.
Питание электромагнита осуществляется от сети
220 В через выпрямитель.
Указание:
Электромагнит включать на короткое время во избежании его перегрева.
После отключения отодвигать стержень электромагнита в крайнее правое положение (для исключения влияния остаточного магнетизма на колебания маятника).
Измерения и обработка результатов
Получить математический маятник максимальной длины и измерить положение любой точки маятника (например, нижней точки шарика), наблюдая так, чтобы изображение этой точки в зеркале совпадало с самой точкой.
Измерить время 30-50 колебаний. Опыт повторить три раза. Каждый раз перед опытом проверять, будет ли плоскость колебаний маятника параллельна задней стенке корпуса.
Изменить длину маятника на 20-25 см и повторить пункты 1 и 2. Все данные измерений занесите в таблицу 12.1.
Таблица 12.1
№
|
n
|
L1, м
|
t1, с
|
L2, м
|
t2, с
|
1
2
3
|
|
|
|
|
|
|
|
|
|
ср.
|
–
|
–
|
|
–
|
|
Вычислить по формуле (12.7) ускорение свободного падения.
Вычислить относительную и абсолютную погрешности измерений g по формулам:
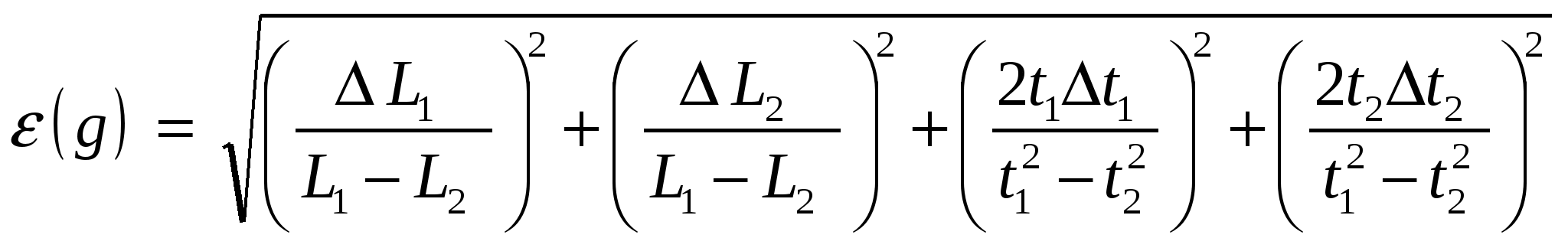 , ,
∆ g = ε(g) · g .
Результат представить в виде:
g = g ± ∆g.
Сравнить полученное значение ускорения свободного падения с табличным.
|
|
|
 Скачать 1.9 Mb.
Скачать 1.9 Mb.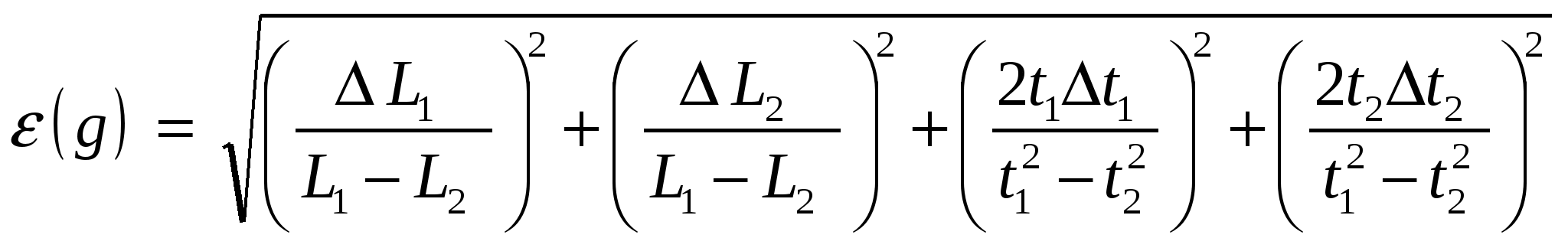 ,
, 
 сли маятник отклонить (рис. 12.1) от положения равновесия (В) на угол α, а затем предоставить самому себе, он будет совершать колебательное движение около положения равновесия. Это свободные колебания. В отсутствие трения свободные колебания вызываются равнодействующей двух сил: силы тяжести
сли маятник отклонить (рис. 12.1) от положения равновесия (В) на угол α, а затем предоставить самому себе, он будет совершать колебательное движение около положения равновесия. Это свободные колебания. В отсутствие трения свободные колебания вызываются равнодействующей двух сил: силы тяжести  атематический маятник, используемый в этой работе – это тяжелый металлический шарик 3, подвешенный на нити (см. рис. 12.2). Маятник вмонтирован в деревянный корпус 2 со стеклянной дверкой. Длину нити можно измерять с помощью ручки 1. На задней стенке корпуса находится зеркало 5 со шкалой для отсчета изменения длины маятника и металлическая нить 7, фиксирующая максимальный угол отклонения маятника от положения равновесия.
атематический маятник, используемый в этой работе – это тяжелый металлический шарик 3, подвешенный на нити (см. рис. 12.2). Маятник вмонтирован в деревянный корпус 2 со стеклянной дверкой. Длину нити можно измерять с помощью ручки 1. На задней стенке корпуса находится зеркало 5 со шкалой для отсчета изменения длины маятника и металлическая нить 7, фиксирующая максимальный угол отклонения маятника от положения равновесия.