Мех_нефиз_240_24.10.2011. Мех_нефиз_240_24.10. Учебнометодический комплекс по дисциплине для нефизических специальностей Лабораторный практикум Абакан 2011 ббк 22. 2я73
 Скачать 1.9 Mb.
|
Контрольные вопросы
Лабораторная работа 14 ОПРЕДЕЛЕНИЕ СКОРОСТИ ЗВУКА МЕТОДОМ СДВИГА ФАЗ Цели работы: определить длину звуковой волны в воздухе; вычислить скорость звука; проанализировать зависимость длины волны от частоты. Приборы и принадлежности: звуковой генератор, электронный осциллограф, микрофон, динамик, измерительная линейка. Библиографический список: [1] § 145, § 153, § 158; [2] ч.1 § 29, § 32 – 33, § 36; [3] т.1 § 57; [4] т.1 § 53, § 61 - 62; [5] § 1.10, § 11.7–11.9; [7] § 3.1.2. Введение Траектория точки, участвующей в двух взаимно-перпендикулярных колебаниях одинаковых частот ω, представляет собой эллипс. Если эти колебания происходят по законам х = Хmcos ωt, (14.1) y= Ymcos(ωt – φ), (14.2) то уравнение эллипса имеет вид:  . (14.3)Здесь Хm и Ym – амплитуды колебаний; φ – сдвиг фаз этих колебаний (разность фаз). Форма эллипса изменяется при изменении φ. При φ= 0 эллипс вырождается в прямую, проходящую в 1 и 3 квандрантах, при φ= π – в прямую, проходящую во 2 и 4 квандрантах. При каждом изменении φ на 2π форма эллипса (в частном случае форма вышеуказанных прямых) повторяется. Это свойство траектории результирующего колебания можно использовать, как будет показано ниже, для определения скорости распространения звука в воздухе. Звуком (или звуковой волной) называется процесс распространения механических колебаний частотой примерно от 20 до 20000 Гц в упругой среде. Источником звука служит любое колеблющееся тело. В различных средах звук от одного и того же источника распространяется с различной скоростью. Скорость распространения звука в газах равна:  , (14.4)где М – молярная масса газа, Т – его температура по шкале Кельвина,  – отношение теплоемкостей газа (Ср – при постоянном давлении, СV – при постоянном объёме), R – универсальная газовая постоянная.Длина звуковой волны λ, частота ν и скорость звука υ связаны соотношением: υ = λν. (14.5) Т 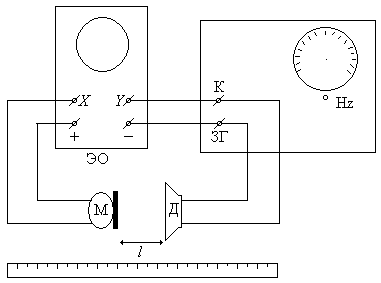 еория метода и описание экспериментальной установкиУстановка, используемая в работе (рис. 14.1), состоит из звукового генератора ЗГ, динамика Д, микрофона М, измерительной шкалы (линейки) и электронного осциллографа ЭО (или ОЭШ). Микрофон и динамик могут передвигаться. З Рис. 14.1. Схема лабораторной установки вуковой генератор питает динамик Д, который служит источником звука. Звук, распространяясь в воздухе, достигает микрофона М и порождает в его цепи переменное напряжение. Это напряжение поступает на вертикально отклоняющие пластины (вход X) электронного осциллографа. На горизонтальные пластины осциллографа (вход Y) напряжение попадает с выходных клемм «К» звукового генератора. Напряжение от звукового генератора и микрофона вызывают взаимно-перпендикулярные колебания электронного луча соответственно уравнениям: х= Хmcosωt, (14.6) y = Ymcosω(t – t/), (14.7)  , (14.8)где t/ – время прохождения звуком расстояния от динамика до микрофона, υ – скорость звука. Согласно (14.6), (14.7), (14.8) разность фаз между указанными выше колебаниями равна:  . (14.9)При изменении l (передвижении микрофона относительно динамика) будет изменяться φ, а, следовательно, изменится траектория движения электронного луча (картина на экране осциллографа). При значениях Δφ, удовлетворяющих условию: Δφ=2πn, (14.10) где n= 1,2,3,…. картина на экране осциллографа будет одинакова. Можно показать, что при этом расстояние между микрофоном и динамиком изменится на Δl. Из уравнений (14.10), (14.9), (14.5) имеем: Δl=nλ. (14.11) Таким образом, чтобы на экране осциллографа видеть одну и ту же картину, нужно передвигать микрофон относительно динамика на расстояние Δl= λ; 2λ и т.д. В этом суть метода определения длины звуковой волны методом сдвига фаз. Измерения и обработка результатов
Каждое положение микрофона уточнить, для чего, отодвинув микрофон немного вправо (или влево), вернуть его в прежнее положение.
Таблица 14.1
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||