еееее. Учебнометодическое пособие к лабораторнопрактическим занятиям по дисциплине Введение в информационные технологии для студентов направления подготовки 44. 03. 04 Профессиональное обучение всех форм обучения
 Скачать 1.6 Mb.
|
Индивидуальные задания к лабораторной работе №1"Представление информации в ЭВМ" Цифра Х в числах обозначает номер вашего варианта 1. Перевести из произвольной системы счисления в десятичную: X721,1728 X234,125 X1011,0012 XD1A4,F316 2. Перевести из десятичной системы счисления в произвольную: X6493510 → в систему счисления с основанием 16 X2910 → в систему счисления с основанием 8 X1310 → в систему счисления с основанием 2 X511010 → в систему счисления с основанием 12 X61310 → в систему счисления с основанием 5 3. Перевести десятичные дроби в произвольную систему счисления: 0,12510 → в систему счисления с основанием 16 0,37510 → в систему счисления с основанием 8 0,32812510 → в систему счисления с основанием 2 0,02410 → в систему счисления с основанием 5 0,414062510 → в систему счисления с основанием 2 4. Перевести из бит в Кбайт: X429217 бит X424719 бит 5. Перевести из Кбайт в бит: X301 Кбайт X274 Кбайт 317 Байт 2 бит 6. Подсчитать количество информации в вашей фамилии, имени и отчестве, если они между собой разделены пробелом и закодированы в коде ASCII, затем – Unicode. Содержание отчета Задание и цель работы. Схема перевода чисел. Описание перевода чисел. Технология выполнения работы В данной работе необходимо перевести в нужную по заданию систему счисления числа, записать ход рассуждений и полученные результаты. Произвести обратный перевод для проверки правильности. Далее необходимо вычислить количество информации, занимаемое вашими данными по формуле Р. Хартли. Затем перевести данные из Кбайт в бит и из бит в Кбайт. Вопросы для защиты работы1. Во сколько раз увеличится число 10,12 при переносе запятой на один знак вправо? 2. Какое минимальное основание может иметь система счисления, если в ней записано число 23? 3. Перевести числа из десятичной системы в требуемую: 4810 → в систему счисления с основанием 2 1610 → в систему счисления с основанием 8 11011110112 → в систему счисления с основанием 10 7B816 → в систему счисления с основанием 10 4. Сравните числа: 111012 и 1D16. 5. Переведите в нужную систему счисления: 1111010010002 → в систему счисления с основанием 16 11000011112 → в систему счисления с основанием 8 4F3D16 → в систему счисления с основанием 2 7138 → в систему счисления с основанием 2 6. Как перевести в биты значение, заданное в байтах и Кбайтах? 7. Как перевести в Кбайт значение, заданное в байтах или в битах? 8. Вычислить количество информации в слове «студент». Лабораторная работа №2. Алгебра логикиЦель работы: Изучить основы алгебры логики. Задачи лабораторной работы В результате прохождения занятия студент должен: 1. знать: определения основных понятий (простое и сложное высказывания, логические операции, логические выражения, логическая функция); порядок выполнения логических операций; алгоритм построения таблиц истинности; схемы базовых логических элементов; законы логики и правила преобразования логических выражений; 2. уметь: применять загоны логики для упрощения логических выражений; строить таблицы истинности; строить логические схемы сложных выражений. Общие теоретические сведения Основные понятия алгебры логики Логической основой компьютера является алгебра логики, которая рассматривает логические операции над высказываниями. Алгебра логики – это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними. Логическое высказывание – это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно. Пример. «3 – простое число» является высказыванием, поскольку оно истинно. Не всякое предложение является логическим высказыванием. Пример. Предложение «Давайте пойдем в кино» не является высказыванием. Вопросительные и побудительные предложения высказываниями не являются. Высказывательная форма – это повествовательное предложение, которое прямо или косвенно содержит хотя бы одну переменную и становится высказыванием, когда все переменные замещаются своими значениями. Пример. «x+2>5» - высказывательная форма, которая при x>3 является истинной, иначе ложной. Алгебра логики рассматривает любое высказывание только с одной точки зрения – является ли оно истинным или ложным. Слова и словосочетания «не», «и», «или», «если..., то», «тогда и только тогда» и другие позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются логическими связками. Высказывания, образованные из других высказываний с помощью логических связок, называются составными (сложными). Высказывания, которые не являются составными, называются элементарными (простыми). Пример. Высказывание «Число 6 делится на 2» - простое высказывание. Высказывание «Число 6 делится на 2, и число 6 делится на 3» - составное высказывание, образованное из двух простых с помощью логической связки «и». Истинность или ложность составных высказываний зависит от истинности или ложности элементарных высказываний, из которых они состоят. Чтобы обращаться к логическим высказываниям, им назначают имена. Пример. Обозначим через А простое высказывание «число 6 делится на 2», а через В простое высказывание «число 6 делится на 3». Тогда составное высказывание «Число 6 делится на 2, и число 6 делится на 3» можно записать как «А и В». Здесь «и» – логическая связка, А, В – логические переменные, которые могут принимать только два значения – «истина» или «ложь», обозначаемые, соответственно, «1» и «0». Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение (табл. 1). Таблица 1. - Основные логические операции
НЕ Операция, выражаемая словом «не», называется отрицанием и обозначается чертой над высказыванием (или знаком ¬). Высказывание ¬А истинно, когда A ложно, и ложно, когда A истинно. Пример. Пусть А=«Сегодня пасмурно», тогда ¬А=«Сегодня не пасмурно». И Операция, выражаемая связкой «и», называется конъюнкцией (лат. conjunctio – соединение) или логическим умножением и обозначается точкой « • » (может также обозначаться знаками  или &). Высказывание А • В истинно тогда и только тогда, когда оба высказывания А и В истинны. Пример. Высказывание «Число 6 делится на 2, и число 6 делится на 3» - истинно, а высказывание «Число 6 делится на 2, и число 6 больше 10» - ложно. ИЛИ Операция, выражаемая связкой «или» (в неисключающем смысле этого слова), называется дизъюнкцией (лат. disjunctio – разделение) или логическим сложением и обозначается знаком  (или плюсом). Высказывание А В ложно тогда и только тогда, когда оба высказывания А и В ложны.Пример: Высказывание «Число 6 делится на 2 или число 6 больше 10» - истинно, а высказывание «Число 6 делится на 5 или число 6 больше 10» - ложно. ЕСЛИ … ТО Операция, выражаемая связками «если …, то», «из … следует», «... влечет …», называется импликацией (лат. implico – тесно связаны) и обозначается знаком → . Высказывание А→В ложно тогда и только тогда, когда А истинно, а В ложно. Пример. Высказывание «если студент сдал все экзамены на «отлично», то он получит стипендию». Очевидно, эту импликацию следует признать ложной лишь в том случае, когда студент сдал на «отлично» все экзамены, но стипендии не получил. В остальных случаях, когда не все экзамены сданы на «отлично» и стипендия получена (например, в силу того, что студент проживает в малообеспеченной семье) либо когда экзамены вообще не сданы и о стипендии не может быть и речи, импликацию можно признать истинной. РАВНОСИЛЬНО Операция, выражаемая связками «тогда и только тогда», «необходимо и достаточно», «... равносильно …», называется эквиваленцией или двойной импликацией и обозначается знаком ↔ или . Высказывание А↔В истинно тогда и только тогда, когда значения А и В совпадают. Пример: Высказывание «Число является четным тогда и только тогда, когда оно делится без остатка на 2» является истинным, а высказывание «Число является нечетным тогда и только тогда, когда оно делится без остатка на 2» - ложно. ЛИБО … ЛИБО Операция, выражаемая связками «Либо … либо», называется исключающее ИЛИ или сложением по модулю 2 и обозначается XOR или  . Высказывание А В истинно тогда и только тогда, когда значения А и В не совпадают.Пример. Высказывание «Число 6 либо нечетно либо делится без остатка на 2» является истинным, а высказывание «Либо число 6 четно либо число 6 делится на 3» – ложно, так как истинны оба высказывания входящие в него. Замечание. Импликацию можно выразить через дизъюнкцию и отрицание:  .Эквиваленцию можно выразить через отрицание, дизъюнкцию и конъюнкцию:  .Исключающее ИЛИ можно выразить через отрицание, дизъюнкцию и конъюнкцию:  .Вывод. Операций отрицания, дизъюнкции и конъюнкции достаточно, чтобы описывать и обрабатывать логические высказывания. Порядок выполнения логических операций задается круглыми скобками. Но для уменьшения числа скобок договорились считать, что сначала выполняется операция отрицания («не»), затем конъюнкция («и»), после конъюнкции – дизъюнкция («или») и исключающего или и в последнюю очередь – импликация и эквиваленция. С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой (логическим выражением). Логическая формула - это символическая запись высказывания, состоящая из логических величин (констант или переменных), объединенных логическими операциями (связками). Логическая функция - это функция логических переменных, которая может принимать только два значения: 0 или 1. В свою очередь, сама логическая переменная (аргумент логической функции) тоже может принимать только два значения: 0 или 1. Пример.  – логическая функция двух переменных A и B.Значения логической функции для разных сочетаний значений входных переменных – или, как это иначе называют, наборов входных переменных – обычно задаются специальной таблицей. Такая таблица называется таблицей истинности. Приведем таблицу истинности основных логических операций (табл. 2) Таблица 2. - Истинности основных логических операций
Опираясь на данные таблицы истинности основных логических операций можно составлять таблицы истинности для более сложных формул. Алгоритм построения таблиц истинности для сложных выражений: 1. Определить количество строк: количество строк = 2n + строка для заголовка, n - количество простых высказываний. 2. Определить количество столбцов: количество столбцов = количество переменных + количество логических операций; определить количество переменных (простых выражений); определить количество логических операций и последовательность их выполнения. Пример 1. Составить таблицу истинности для формулы И–НЕ, которую можно записать так:  .1. Определить количество строк: На входе два простых высказывания: А и В, поэтому n=2 и количество строк =22+1=5. 2. Определить количество столбцов: Выражение состоит из двух простых выражений (A и B) и двух логических операций (1 инверсия, 1 конъюнкция), т.е. количество столбцов таблицы истинности = 4. 3. Заполнить столбцы с учетом таблиц истинности логических операций (табл. 3). Таблица 3. - Таблица истинности для логической операции
Подобным образом можно составить таблицу истинности для формулы ИЛИ–НЕ, которую можно записать так:  .Таблица 4. - Таблица истинности для логической операции
Примечание: И–НЕ называют также «штрих Шеффера» (обозначают | ) или «антиконъюнкция»; ИЛИ–НЕ называют также «стрелка Пирса» (обозначают ↓) или «антидизъюнкция». Пример 2. Составить таблицу истинности логического выражения  .Решение: 1. Определить количество строк: На входе два простых высказывания: А и В, поэтому n=2 и количество строк=22+1= 5. 2. Определить количество столбцов: Выражение состоит из двух простых выражений (A и B) и пяти логических операций (2 инверсии, 2 конъюнкции, 1 дизъюнкция), т.е. количество столбцов таблицы истинности = 7. Сначала выполняются операции инверсии, затем конъюнкции, в последнюю очередь операция дизъюнкции. 3. Заполнить столбцы с учетом таблиц истинности логических операций (табл. 5). Таблица 5. - Таблица истинности для логической операции
Логические формулы можно также представлять с помощью языка логических схем. Существует три базовых логических элемента, которые реализуют три основные логические операции: логический элемент «И» – логическое умножение – конъюнктор; логический элемент «ИЛИ» – логическое сложение – дизъюнктор; логический элемент «НЕ» – инверсию – инвертор. 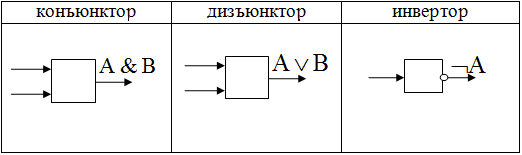 Поскольку любая логическая операция может быть представлена в виде комбинации трех основных, любые устройства компьютера, производящие обработку или хранение информации, могут быть собраны из базовых логических элементов, как из “кирпичиков”. Логические элементы компьютера оперируют с сигналами, представляющими собой электрические импульсы. Есть импульс – логический смысл сигнала – 1, нет импульса – 0. На входы логического элемента поступают сигналы-значения аргументов, на выходе появляется сигнал-значение функции. Преобразование сигнала логическим элементом задается таблицей состояний, которая фактически является таблицей истинности, соответствующей логической функции, только представлена в форме логических схем. В такой форме удобно изображать цепочки логических операций и производить их вычисления. Алгоритм построения логических схем. Определить число логических переменных. Определить количество логических операций и их порядок. Изобразить для каждой логической операции соответствующий ей логический элемент. Соединить логические элементы в порядке выполнения логических операций. Пример. По заданной логической функции  построить логическую схему.Решение. Число логических переменных = 2 (A и B). Количество операций = 5 (2 инверсии, 2 конъюнкции, 1 дизъюнкция). Сначала выполняются операции инверсии, затем конъюнкции, в последнюю очередь операция дизъюнкции. Схема будет содержать 2 инвертора, 2 конъюнктора и 1 дизъюнктор. Построение надо начинать с логической операции, которая должна выполняться последней. В данном случае такой операцией является логическое сложение, следовательно, на выходе должен быть дизъюнктор. На него сигналы подаются с двух конъюнкторов, на которые, в свою очередь, подаются один входной сигнал нормальный и один инвертированный (с инверторов). 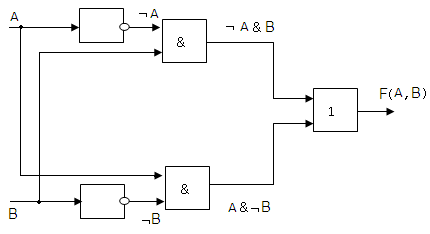 Логические законы и правила преобразования логических выражений Если две формулы А и В одновременно, то есть при одинаковых наборах значений входящих в них переменных, принимают одинаковые значения, то они называются равносильными. В алгебре логики имеется ряд законов, позволяющих производить равносильные преобразования логических выражений. 1. Закон двойного отрицания:  ;2. Переместительный (коммутативный) закон: для логического сложения:  ;для логического умножения:  ;3. Сочетательный (ассоциативный) закон: для логического сложения:  ;для логического умножения:  ;4. Распределительный (дистрибутивный) закон: для логического сложения:  ;для логического умножения:  ;5. Законы де Моргана: для логического сложения:  ;для логического умножения:  ;6. Закон идемпотентности: для логического сложения:  ;для логического умножения:  ;7. Законы исключения констант: для логического сложения:  ;для логического умножения:  ;8. Закон противоречия:  ;9. Закон исключения третьего:  ;10. Закон поглощения: для логического сложения:  ;для логического умножения:  ;11. Правило исключения импликации:  ;12. Правило исключения эквиваленции:  .Справедливость этих законов можно доказать составив таблицу истинности выражений в правой и левой части и сравнив соответствующие значения. Основываясь на законах, можно выполнять упрощение сложных логических выражений. Такой процесс замены сложной логической функции более простой, но равносильной ей, называется минимизацией функции. Пример. Упростить логическое выражение  .Решение: Согласно закону де Моргана:  .Согласно сочетательному закону:  .Согласно закону противоречия и закону идемпотентности:  .Согласно закону исключения 0:  Окончательно получаем  |
